扩展功能
文章信息
- 肖庆一, 仇云强, 胡海学, 王文斌, 庞兴亮.
- XIAO Qingyi, QIU Yunqiang, HU Haixue, WANG Wenbin, PANG Xingliang
- 基于LSTM和PSO-LSTM的水泥稳定再生骨料强度预测模型
- LSTM and PSO-LSTM based cement stabilized recycled aggregate strength prediction model
- 公路交通科技, 2025, 42(9): 44-52
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(9): 44-52
- 10.3969/j.issn.1002-0268.2025.09.005
-
文章历史
- 收稿日期: 2023-04-23
2. 华设检测科技有限公司, 江苏 南京 210014;
3. 天津市交通科学研究院, 天津 300074;
4. 沧州路桥建设集团有限公司, 河北 沧州 061000
2. China Design Group Testing Technology Co., Ltd., Nanjing, Jiangsu 210014, China;
3. Tianjin Transportation Research Institute, Tianjin 300074, China;
4. Cangzhou Road & Bridge Construction Group Co., Ltd., Cangzhou, Hebei 061000, China
随着城市规划变迁、道路与建筑使用寿命到期,会产生大量水泥混凝土类废弃物,即建筑垃圾。道路修筑材料的开采和运输会造成扬尘、山体破坏等,严重影响开采地区环境生态。保护环境政策不断出台,严格限制了公路、铁路等基础设施建设原材料获取途径和产量。建筑垃圾经过处理生产出再生骨料,并应用于道路结构中是解决建筑垃圾堆放、处理、再利用难题的一种新处理方式[1-2]。经过水泥稳定之后,混合料自身力学性能满足道路基层中应用的要求,具有广阔的应用前景。再生骨料的力学性能具有一定不匀质性,并且具有较大吸水率、较小压碎值等物理性质。道路结构中应用再生骨料前需要进行力学验证。规范对水泥稳定材料的7 d无侧限抗压强度有明确且详细的要求。用7 d无侧限抗压强度衡量混合料配比好坏。传统配合比设计需要进行大量试验并且试验周期较长,同时水泥稳定类材料强度具有成长规律,如果可以依据已有试验数据对目标龄期的水稳再生骨料材料进行强度预测,可以提高配合比设计的效率,缩短配合比试验周期。
近些年来,人工智能学科中预测模型的快速发展,可以为传统道路材料配合比设计方法提供新思路,有很多学者将神经网络应用于水泥混凝土材料强度预测当中,其中出现很多优秀的预测模型,其精度可以达到95%[3-4]以上。传统神经网络存在易陷入局部最优情况,同时也面临着梯度消失和梯度爆炸困扰。长短期记忆网络模型(Long Short-Term Memory Network, LSTM)通过建立单元遗忘门,解决了梯度消失和梯度爆炸的困扰[5-7]。PSO被用于对神经网络参数进行全局寻优,以解决网络陷入局部最优的情况。优化算法和预测模型在快速发展的同时,却鲜有应用于水泥稳定材料模型。为填补这一空白,更加准确地预测水泥稳定再生骨料材料的无侧限抗压强度,从而加速配合比设计流程,提高配合比设计效率。本研究以实际试验数据作为数据集,搭建LSTM和PSO-LSTM强度预测模型,并根据试验数据集,进行相关参数和无侧限抗压强度相关性分析。
1 构建PSO-LSTM递归神经网络模型 1.1 特征选择水泥稳定材料强度形成机理包括物理作用、化学反应、物理化学反应等多种复杂作用。工程中,通过碾压水泥和级配骨料混合物形成骨架嵌挤作用,同时水泥水化反应发生,强度开始形成。随着龄期增长,水泥水化反应持续进行,水泥稳定材料强度持续增长。根据水泥稳定材料强度形成机理[8],可以得出:水泥稳定材料强度影响因素和骨料级配、水泥剂量、龄期、含水量、密实度有关。由于研究中使用再生骨料替代部分天然骨料,对水泥稳定材料强度的影响产生了新变量:再生骨料因为性能具有一定缺陷,例如骨料内部和表面具有微裂缝,导致吸水率变大、骨料强度变小,再生骨料密度小,同时再生骨料有受力薄弱的新旧砂浆交接区。所以模型构建时必须将再生骨料替代率、混合骨料吸水率、混合骨料压碎值这3个变量加入。
结合以上原因,本次模型特征选择为:含水率、水泥剂量、再生骨料替代率、养护龄期、混合骨料压碎值、0~5 mm骨料占比、5~10 mm骨料占比、10~20 mm骨料占比、20~30 mm骨料占比、饱水密度和混合骨料吸水率一共11个因素作为递归神经网络输入层,以无侧限抗压强度作为输出层。
1.2 试验设计与结果以往学者做了大量关于水泥稳定材料、水泥稳定再生骨料材料的无侧限抗压强度,并分别得到试验数据。水泥稳定再生骨料材料无侧限抗压强度受闷料时间、成型方式、养护条件、原材料性质等多方面因素影响,并且鲜有学者研究各种配比的水泥稳定再生骨料材料强度成长趋势影响因素。所以将以往学者的数据应用于模型训练,会造成模型预测精度不佳、误差较大。所以本次数据集均来源于试验所获数据。
为探究上述11个特征值对水泥稳定材料强度影响,通过改变各个材料掺量,形成不同配比混合料,在不同龄期进行无侧限抗压强度试验。
试验水泥采用天津地区马牌标号为P.O 42.5普通硅酸盐水泥,水泥细度为3.5%,初凝时间为245 min,终凝时间为415 min。主要性能指标见表 1。
| 性能指标 | 初凝/min | 终凝/min | 比表面积/(m2·kg―1) | 安定性/m | 抗折强度/MPa | 抗压强度/MPa | |||
| 3 d | 28 d | 3 d | 28 d | ||||||
| 实测数据 | 245 | 415 | 360 | 合格 | 3.8 | 8.5 | 18.6 | 44.7 | |
| 规范要求 | ≥180 | 360~600 | ≥300 | 标准法 | ≥3.5 | ≥6.5 | ≥17 | ≥42.5 | |
试验用再生骨料选取天津市宝坻再生骨料生产厂生产的再生骨料,主要性能指标经过试验,见表 2。
| 项目 | Ⅰ类再生骨料技术要求 | 实测值 |
| 表观密度/(g·cm―3) | ≥2 250 | 2 762 |
| 压碎指标/% | <30 | 22 |
| 轻质杂物含量/% | ≤0.1 | ≤0.1 |
| 再生混凝土颗粒含量/% | ≥40 | 89.5 |
| 微粉含量/% | <3.0 | 2.73 |
| 吸水率/% | <8 | 7.6 |
| 针片状颗粒含量/% | <10 | 6.4 |
| 有机物含量/% | 合格 | 合格 |
水泥作为胶凝材料,掺加量越大,混合料的抗压性能越好,抗弯拉性能越差,同时结合工程造价与实际施工经验,掺加4%~6%水泥的混合料满足道路基层、底基层的强度要求。通过室内击实试验,在再生骨料替代率30%时,最大干密度对应的最佳含水率为5.8%,考虑到再生骨料多空隙,吸水率大,需水量比天然骨料多,故增加含水率和吸水率影响因素。再生骨料物理力学性能与天然骨料具有差异,从而影响混合料强度,故增加再生骨料替代率影响因素。水泥稳定材料强度与水泥水化程度有密切关联,水泥随养护时间延长,水化充分,混合料强度越大,故增加龄期影响因素。压碎值越小的石料,抗压性能越稳定,再生骨料压碎值较大,故增加压碎值的影响因素。不同的石料级配形成不同骨架类型的混合料,故增加级配影响因素,通过不同粒径骨料的掺加百分比表征。
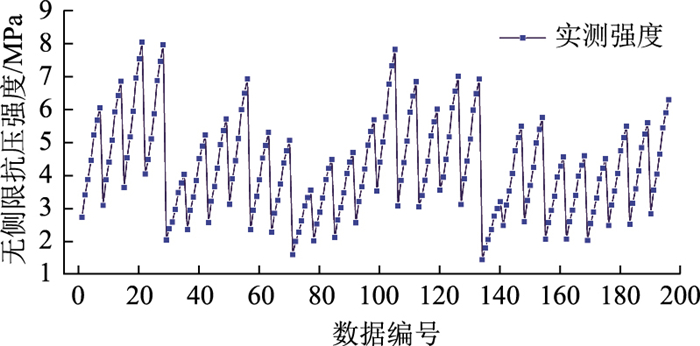
试验配比方面:水泥剂量分别为4%,5%,6%;含水率分别为5.8%,6%,7%,8%;再生骨料替代率分别为30%,50%,80%;龄期分别为3 d,7 d,10 d,14 d,20 d,24 d,28 d;级配类型分别为骨架-空隙结构、骨架-密实结构,密实-悬浮结构。部分试验配比详情见表 3。本次无侧限抗压强度一共196组数据集。实测强度数据见图 1。
| 含水率/% | 水泥剂量/% | 替代率/% | 龄期/d | 压碎值 | 0~5 mm 骨料/% |
5~10 mm 骨料/% |
10~20 mm 骨料/% |
20~30 mm 骨料/% |
密度/(g·cm―3) | 吸水率/% |
| 8.0 | 4 | 30 | 3 | 14.3 | 30 | 22 | 30 | 18 | 2.45 | 2.67 |
| 7.0 | 5 | 30 | 3 | 14.3 | 30 | 22 | 30 | 18 | 2.33 | 2.67 |
| 6.0 | 6 | 30 | 24 | 14.3 | 30 | 22 | 30 | 18 | 2.44 | 2.67 |
| 5.8 | 4 | 30 | 8 | 14.3 | 35 | 35 | 17 | 13 | 2.46 | 2.77 |
| 5.8 | 4 | 50 | 20 | 16.5 | 35 | 35 | 17 | 13 | 2.50 | 3.68 |
| 5.8 | 4 | 50 | 10 | 16.5 | 15 | 35 | 15 | 35 | 2.50 | 4.53 |
| 7.0 | 5 | 80 | 14 | 22.0 | 30 | 22 | 30 | 18 | 2.47 | 2.67 |
|
| 图 1 实测强度 Fig. 1 Tested strength |
| |
1.3 网络搭建
确定输入层为11个参数,输出层为1个参数后,对预测网络进行搭建。
循环神经网络(Recurrent Neural Network, RNN)的输入一般是一组相关联的序列数据[9],本研究中水泥稳定再生骨料材料无侧限抗压强度通过龄期等相互关联。但是基础RNN迭代原理就决定了梯度消失和梯度爆炸必定会产生困扰。
根据图 2和图 3中RNN网络结构,t时刻神经元接收隐藏单元t-1时刻数据输出值,并在t时刻数据计算完成后,传入t+1时刻神经元。因此RNN在某一时刻的状态,是基于过去所有状态,即当前状态是依赖于先前状态。RNN前向计算按照时间序列展开,然后使用基于时间的反向传播算法(Back Propagation Through Time,BPTT)[10]对网络中参数进行更新,也是目前循环神经网络最常用的训练算法。基于梯度的学习需要模型参数θ和损失函数L之间存在闭式解,根据估计值和实际值之间误差来最小化损失函数,那么在损失函数上计算得到的梯度信息可以传回给模型参数并进行相应修改。如果定义x1, x2, x3, ..., xt是1到t时刻神经元输入值,通过上述BPTT算法,即St=Fθ(St-1, xt),将t-1时刻状态St-1映射到下一时刻状态St中。定义T时刻损失函数为LT,关于参数的梯度计算如式(1)所示。
| $ \nabla_\theta L_T=\frac{\partial L_T}{\partial \boldsymbol{\theta}}=\sum\limits_{t \leqslant T} \frac{\partial L_T}{\partial \boldsymbol{s}_T} \frac{\partial \boldsymbol{s}_T}{\partial \boldsymbol{s}_t} \frac{\partial F_\theta\left(\boldsymbol{s}_{t-1}, \boldsymbol{x}_t\right)}{\partial \boldsymbol{\theta}}。$ | (1) |

|
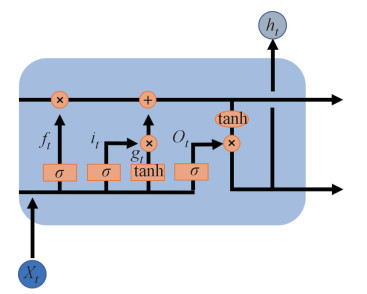
| 图 2 LSTM神经元结构图 Fig. 2 LSTM structure |
| |
|
| 图 3 LSTM单个神经元结构图 Fig. 3 Single neural structure of LSTM |
| |
根据链式法则,将式(1)中
| $ \frac{\partial \boldsymbol{s}_T}{\partial \boldsymbol{s}_t}=\frac{\partial \boldsymbol{s}_T}{\partial \boldsymbol{s}_{T-1}} \frac{\partial \boldsymbol{s}_{T-1}}{\partial \boldsymbol{s}_{T-2}} \cdots \frac{\partial \boldsymbol{s}_{t+1}}{\partial \boldsymbol{s}_t}=f_T^{\prime} f_{T-1}^{\prime} \cdots f_{1 }^{\prime}。$ | (2) |
RNN进行数据计算时,若|ft′| < 1[11],当神经元数量变多时,fT′ fT-1′…f1′值将会变小,当神经元达到一定数量,fT′ fT-1′…f1′将趋近于0,根据公式(1)和公式(2),此时梯度
为解决梯度消失或者梯度爆炸,基于RNN改进模型LSTM[12]通过引入门来进行数据运算和传递。LSTM单元模型见图 2和图 3。图 2和图 3中“σ”表示输入激活函数sigmoid,“tanh”表示输出激活函数tanh,“×”表示矩阵相乘,“+”表示矩阵相加。
LSTM网络的每个单元由3个乘法门连接组成,即输入门(it)、遗忘门(ft)和输出门(ot)门,考虑到每个门内部单元构造,对应功能可以理解为写入、重置和读取操作。存储单元中门便于长时间保持和访问内部单元状态。LSTM输出将取决于所有先前输入。先前信息既不会被完全丢弃,也不会被完全转移到当前状态。相反,先前信息对当前状态影响通过门信号被谨慎控制。
本研究中LSTM递归神经网络门计算公式如下。
| $ f_t=\sigma\left(\boldsymbol{W}_{\mathrm{f}}\left(h_{t-1}, x_{\mathrm{t}}\right)+\boldsymbol{b}_{\mathrm{f}}\right), $ | (3) |
| $ i_t=\sigma\left(\boldsymbol{W}_{\mathrm{i}}\left(h_{t-1}, x_t\right)+\boldsymbol{b}_{\mathrm{i}}\right), $ | (4) |
| $ g_t=\tanh \left(w_{\mathrm{g}}\left(h_{t-1}, x_t\right)+\boldsymbol{b}_{\mathrm{g}}\right), $ | (5) |
| $ c_{\mathrm{t}}=f_t c_{t-1}+i_t g_t, $ | (6) |
| $ o_t=\sigma\left(\boldsymbol{W}_{\mathrm{o}}\left(h_{t-1}, x_t\right)+\boldsymbol{b}_{\mathrm{o}}\right), $ | (7) |
| $ h_t=o_t \tanh \left(c_t\right), $ | (8) |
式中,ft, it, gt和ot分别表示遗忘门、输入门、更新门和输出门的值;Wf, Wi, Wg和Wo分别是4种门权重向量;b表示偏差向量;σ和ct是输入门和输出门激活函数。其中遗忘门ft是LSTM单元最为关键的一环,遗忘门控制着上一时刻单元传递数据信息是否保留,可以在梯度反向传播时避免梯度爆炸或者梯度消失。
根据数据集格式、先前学者建立模型经验并结合计算机硬件水平[13-14],选取参数:units=25,dropout=0.15,batch_size=32, 输入激活函数sigmoid,输出激活函数tanh,epochs=600。
1.4 优化算法粒子群优化算法(Particle Swarm Optimization, PSO)是经典群体智能算法,灵感来源于鸟类飞行和觅食社会活动。其算法特点在于用较少参数设置,实现较为良好的全局搜索。
其原理可以总结如下[15-18]:初始化一群粒子并在迭代中寻找个体极值和全局极值。在找到这2个最好解后,粒子根据如下的式(9) 和式(10)来更新自己的速度和位置。
| $ \overrightarrow{v_{i d}^{k+1}}=\omega V_{i d}^k+c_1 r_1\left(\overrightarrow{p b e s t_{i d}^k}-\overrightarrow{X_{i d}^k}\right)+c_2 r_2\left(\overrightarrow{g b e s t_{i d}^k}-\overrightarrow{X_{i d}^k}\right), $ | (9) |
| $ \overrightarrow{X_{i d}^{k+1}}=\overrightarrow{X_{i d}^k}+\overrightarrow{V_{i d}^{k+1}}, $ | (10) |
式中,Vidk表示粒子i当前速度;Xidk表示粒子i的当前位置;pbestidk表示个体极值;gbestidk表示全局极值;vidk+1表示粒子迭代后的更新速度;Xidk+1表示粒子迭代后的更新位置;ω表示惯性权重,其含义是上一代粒子的速度对当前迭代速度的影响程度;c1、c2表示加速常数;r1、r2表示取值范围在(0, 1)的随机数。
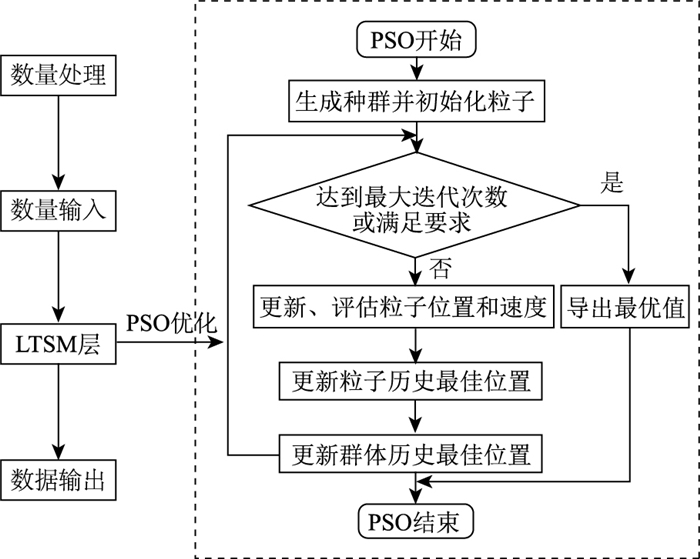
PSO-LSTM的流程图见图 4。
|
| 图 4 PSO-LSTM流程图 Fig. 4 Flowchart of PSO-LSTM |
| |
根据PSO搜索粒子是跟踪全体极值和个体极值分为全局模型和局部模型。在LSTM模型中,神经元数量的提升能显著增加模型精度,但过多的神经元会使模型进入过拟合状态,所以引入dropout对数据进行随机丢弃,避免模型过拟合现象,batch_size对模型训练的速度有显著影响。综上原因,利用PSO的全局模型,在LSTM网络中,寻找神经元(neurals)、随机丢弃率(dropout)和单次传导数据数量(batch_size)的最佳数值。在本研究的PSO-LSTM模型中,PSO算法用于对LSTM的神经元数量(neural),随机丢弃率(dropout)以及单次训练投放数据集数量(batch_size)的最优化搜索。
PSO算法的相关参数见表 4。
PSO-LSTM网络通过PSO算法全局搜索到最佳参数为:神经元数量为29,随机丢弃率为0.21,单次传导数据数量为19。
LSTM和PSO-LSTM网络参数对比见表 5。
| 模型类型 | 神经元数量 | 随机丢弃率 | 单次训练投放数据集数量 |
| LSTM | 25 | 0.15 | 32 |
| PSO-LSTM | 29 | 0.21 | 19 |
2 数据预处理和评价指标选取 2.1 特征选择与数据预处理
数据预处理是决定模型预测准确性的重要部分[19-20],为减少各个输入层之间因为不同单位之间的数级差异对预测结果产生影响,选取最大最小值归一化,将所有试验数据转化为[0, 1]之间的数值,公式如下:
| $ x^{\prime}=\frac{x-\min (x)}{\max (x)-\min (x)}, $ | (11) |
式中,x′表示归一化后的数据值;min(x)和max(x)分别表示数据集中该指标的最小和最大值。
经过归一化的数据在模型训练的过程中能快速拟合并减少误差。
2.2 评价指标选取评价指标选取MSE,RMSE,MAE,MAPE和R2。MSE和RMSE表征预测强度与实测强度的方差和标准差,MAE表征预测强度与实测强度的误差值,MAPE表征预测强度和实测强度的平均绝对百分比误差值。其中MSE,RMSE,MAE,MAPE的值越趋于0,模型误差越小,模型预测精度越高。R2表征实测强度与预测强度的平方差和与实测强度与平均强度的平方差和之比,越接近1,表示模型拟合效果越好。
5种评价指标的计算公式如下。
| $ \mathrm{MSE}=\frac{1}{n} \sum\limits_{i=1}^n\left(\widehat{y}_i-y_i\right)^2, $ | (12) |
| $ \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(\widehat{y}_i-y_i\right)^2}, $ | (13) |
| $ \mathrm{MAE}=\frac{1}{n} \sum\limits_{i=1}^n\left|\widehat{y}_i-y_i\right|, $ | (14) |
| $ \mathrm{MAPE}=\frac{100 \%}{n} \sum\limits_{i=1}^n\left|\frac{\widehat{y}_i-y_i}{y_i}\right|, $ | (15) |
| $ o_t=\sigma\left(W_o\left(h_{t-1}, x_t\right)+b_o\right), $ | (16) |
| $ R^2=1-\frac{\sum\limits_i\left(\widehat{y}_i-y_i\right)^2}{\sum\limits_i\left(\bar{y}_i-y_i\right)^2}, $ | (17) |
式中,yi表示实测强度;yi表示实测强度均值;
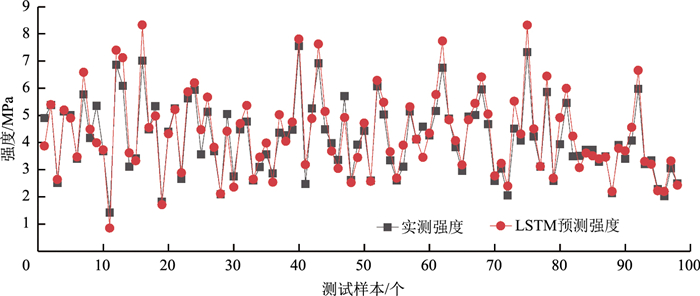
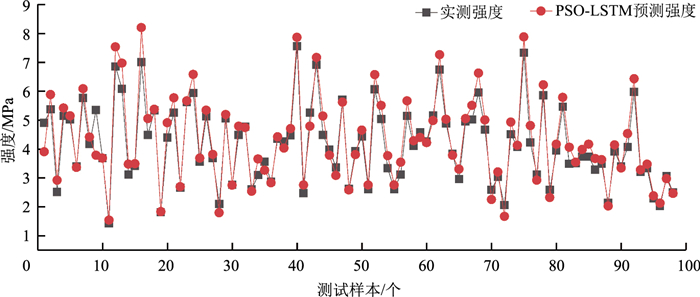
LSTM和PSO-LSTM预测结果见图 5和图 6。通过绘图软件绘制点线图,可以看出2种预测网络均可以实现预测值与实测值紧密拟合。准确率分别达到了98.49%和98.51%。
|
| 图 5 LSTM预测结果 Fig. 5 LSTM prediction result |
| |
|
| 图 6 PSO-LSTM预测结果 Fig. 6 PSO-LSTM prediction result |
| |
3.2 模型分析
根据图 5和图 6所示,LSTM和PSO-LSTM对水泥稳定再生骨料材料强度预测结果和实际试验得到的强度数据基本吻合,预测精度均达到98.5%以上。2种模型都能对不同龄期的水泥稳定再生骨料材料强度进行较精确的预测。同时发现,在测试集中,PSO-LSTM对较小强度值预测较为准确,但在最大的一个强度值预测时出现了较LSTM模型更大的误差。
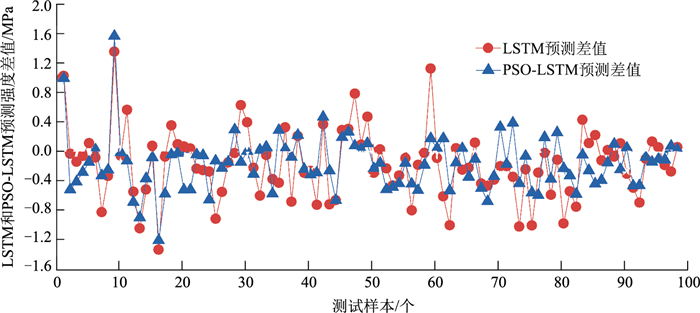
图 7表示为测试集中每一个数据预测值和实测值的差值,一共98个数据点。可以看出,PSO-LSTM模型预测强度值与真实强度值差值的平均值要比LSTM模型更小,模型预测持续性较好。
|
| 图 7 LSTM和PSO-LSTM预测差值对比 Fig. 7 Prediction differences between LSTM and PSO-LSTM |
| |
为进一步探究,PSO-LSTM和LSTM算法优劣,通过表 6的评价指标,可以得出:MSE和RMSE中,经过PSO优化后模型对比未优化模型,优化效果达到了34.48%和19.06%。MAE值和MAPE值分别提高了19.71%和26.21%。说明,经过PSO优化后,模型误差减小,精度更高。同时,R2也提高了5.28%,达到了0.913,具有更好的拟合效果。
| 指标 | LSTM | PSO-LSTM | 优化效果/% |
| MSE | 0.239 | 0.156 6 | 34.48 |
| RMSE | 0.488 9 | 0.395 7 | 19.06 |
| MAE | 0.369 8 | 0.296 9 | 19.71 |
| MAPE | 0.088 7 | 0.070 2 | 20.86 |
| R2 | 0.867 2 | 0.913 0 | 5.28 |
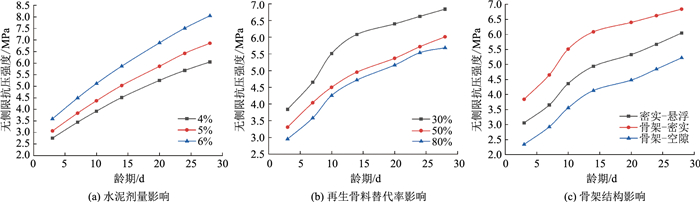
水泥剂量、龄期、骨架类型都是水泥稳定材料强度影响因素。图 8(a)是水泥稳定材料在骨架密实结构、30%再生骨料替代率情况下,在不同水泥剂量影响下的强度与龄期的关系。图 8(b)是水泥稳定材料在骨架密实结构、4%水泥替代率情况下,在不同再生骨料替代率影响下强度与龄期的关系。图 8(c)是水泥稳定材料在4%水泥替代率,30%再生骨料替代率情况下,在不同骨架结构影响下强度与龄期的关系。
|
| 图 8 不同类型对水泥稳定材料强度影响结果 Fig. 8 Influences of different types on cement stabilized material strength |
| |
在模型中,应用相关性分析,将11个输入层分为材料类输入和非材料类输入,以此来表明材料组成和外部条件分别对水泥稳定再生骨料材料影响关系。其中,材料类输入包括了含水率、水泥剂量、0~5 mm骨料含量、5~10 mm骨料含量、10~20 mm骨料含量、20~30 mm骨料含量;非材料类输入包括再生骨料替代率、龄期、压碎值、饱水密度和吸水率。各个参数的相关系数见表 7和表 8。
| 参数 | 强度 | 水泥剂量 | 含水率 | 骨料 | |||
| 0~5 mm | 5~10 mm | 10~20 mm | 20~30 mm | ||||
| 相关系数 | 1.000 0 | 0.404 7 | 0.085 6 | 0.050 6 | ―0.170 5 | 0.278 4 | ―0.150 3 |
| 参数 | 强度 | 龄期 | 密度 | 压碎值 | 替代率 | 吸水率 |
| 相关系数 | 1.000 0 | 0.733 8 | 0.131 8 | 0.016 0 | 0.015 3 | 0.009 4 |
通过对比试验数据结果和相关性分析结果发现:
在材料类影响中,水泥剂量对强度影响的相关系数达到0.404 7,为材料类影响中对混合料强度正影响最大的因素表现为水泥剂量越多,稳定材料的抗压强度越大;龄期对强度影响的相关系数达到0.733 8,是非材料类影响因素中对混合料强度正影响最大的因素,表现为养护龄期越长,稳定材料强度越大。根据相关性系数,5~10 mm和20~30 mm粒径骨料对混合料的强度起到负面影响,2种粒径材料在配比中越多,材料强度越低。
在非材料影响中,龄期对水泥稳定再生骨料强度影响最大,同时这一结论仅代表 28 d内影响关系。试验结果表明,再生骨料替代率越大,水泥稳定材料在相同龄期强度越低,且替代率越低,在早期强度成长值越大。
骨架空隙结构强度为3种结构中最低,由于缺少细集料,导致骨料之间不能紧密粘结,导致早期强度低。骨架悬浮结构因为粗骨料之间没有形成有效嵌挤结构,导致强度偏低。
综上,结合工程造价等因素,推荐水泥稳定再生骨料材料选取4%水泥剂量,30%再生骨料替代率、骨架-密实结构配比设计。
4 结语通过设计不同配比、不同替代率的水泥稳定再生骨料,形成196条无侧限抗压强度数据集,变量包括含水率、水泥剂量、再生骨料替代率、养护龄期、混合骨料压碎值、粒径0~5 mm骨料占比、5~10 mm骨料占比、10~20 mm骨料占比、20~30 mm骨料占比、饱水密度和混合骨料吸水率。
本研究建立了LSTM模型,对水泥稳定再生骨料材料强度进行预测。初始模型预测精度为98.49%。引入PSO,对初始LSTM模型进行参数全局寻优,构建PSO-LSTM模型。新模型预测精度为98.51%。通过引入评价指标,LSTM网络经过PSO优化后MSE、RMSE值提高了34.48%和19.06%;MAE值和MAPE值提高了19.71%和20.86%。同时,R2也提高了5.28%。经过验证,使用经过PSO优化后的LSTM模型进行水泥稳定再生骨料类材料强度预测具有较高的准确性,且模型拟合性更好。
通过对比198条试验结果,考虑水泥剂量、再生骨料替代率和骨架结构影响,得出水泥稳定再生骨料材料选取4%水泥剂量,30%再生骨料替代率、骨架-密实结构的配比设计是较为合理且可行的配合比方案。
将11个变量,根据其影响水泥稳定再生骨料材料原理,分成材料类影响和非材料类影响。通过相关性分析,得出影响水泥剂量和龄期分别是材料类影响和非材料类影响中对抗压强度影响最大的因素。表现为,水泥剂量越大,龄期越大,材料抗压强度越大。同时再生骨料的替代,对早期抗压强度相关系数仅为0.02。可以推出,再生骨料的掺加可以满足路用要求。
本研究建立的模型可以用于水泥稳定再生骨料早期无侧限抗压强度预测,为配合比设计提供预测强度支持,对人工智能应用于传统道路工程配合比设计具有一定指导意义。水泥稳定材料强度随龄期持续增长,但强度在水泥水化结束后停止增长,本模型数据集最长的龄期仅为28 d,因此本模型仅适用于早期强度预测。本研究也可为长期预测模型提供参考和借鉴。
| [1] |
杨军强, 孙欣. 建筑垃圾再生骨料工程特性分析[J]. 施工技术(中英文), 2022, 51(16): 105-109. YANG Junqiang, SUN Xin. Analysis of engineering characteristics of recycled aggregate from construction waste[J]. Construction Technology(Chinese and English), 2022, 51(16): 105-109. |
| [2] |
寇长江, 王芸芸, 肖鹏, 等. 正硅酸乙酯对再生粗骨料物理及表面特性的影响[J]. 公路交通科技, 2022, 39(5): 26-32, 40. KOU Changjiang, WANG Yunyun, XIAO Peng, et al. Influence of tetraethoxysilane on physical and surface properties of recycled coarse aggregates[J]. Journal of Highway and Transportation Research and Development, 2022, 39(5): 26-32, 40. DOI:10.3969/j.issn.1002-0268.2022.05.004 |
| [3] |
FAROOQ F, NASIR AMIN M, KHAN K, et al. A comparative study of random forest and genetic engineering programming for the prediction of compressive strength of high strength concrete (HSC)[J/OL]. Applied Sciences, 2020, 10(20): 7330. (2020-10-20)[2023-04-22]. https://doi.org/10.3390/app10207330.
|
| [4] |
LATIF S D. Concrete compressive strength prediction modeling utilizing deep learning long short-term memory algorithm for a sustainable environment[J].
Environmental Science and Pollution Research, 2021, 28(23): 30294-30302.
DOI:10.1007/s11356-021-12877-y |
| [5] |
AHMAD MIRSALARI S, NAZARI N, SINAEI S, et al. FaCT-LSTM: Fast and compact ternary architecture for LSTM recurrent neural networks[J].
IEEE Design & Test, 2022, 39(3): 45-53.
|
| [6] |
BHANDARI H N, RIMAL B, POKHREL N R, et al. LSTM-SDM: An integrated framework of LSTM implementation for sequential data modeling[J]. Software Impacts, 2022, 14: 100396. (2022-08-01)[2023-04-22]. https://doi.org/10.1016/j.simpa.2022.100396.
|
| [7] |
WAN X B, LIU H, XU H, et al. Network traffic prediction based on LSTM and transfer learning[J].
IEEE Access, 2022, 10: 86181-86190.
DOI:10.1109/ACCESS.2022.3199372 |
| [8] |
蒋应军, 李明杰, 张俊杰, 等. 水泥稳定碎石强度影响因素[J]. 长安大学学报(自然科学版), 2010, 30(4): 1-7. JIANG Yingjun, LI Mingjie, ZHANG Junjie, et al. Influence factors of strength properties of cement stabilization of crushed aggregate[J]. Journal of Chang'an University (Natural Science Edition), 2010, 30(4): 1-7. |
| [9] |
杨丽, 吴雨茜, 王俊丽, 等. 循环神经网络研究综述[J]. 计算机应用, 2018, 38(增2): 1-6, 26. YANG Li, WU Yuxi, WANG Junli, et al. Research on recurrent neural network[J]. Journal of Computer Applications, 2018, 38(S2): 1-6, 26. |
| [10] |
WERBOS P J. Backpropagation through time: What it does and how to do it[J].
Proceedings of the IEEE, 1990, 78(10): 1550-1560.
DOI:10.1109/5.58337 |
| [11] |
BIANCHI F M, LIVI L, ALIPPI C. Investigating echo-state networks dynamics by means of recurrence analysis[J].
IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(2): 427-439.
DOI:10.1109/TNNLS.2016.2630802 |
| [12] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J].
Neural Computation, 1997, 9(8): 1735-1780.
DOI:10.1162/neco.1997.9.8.1735 |
| [13] |
GÉRON A. Hands-on machine learning with Scikit-learn, Keras and Tensorflow[M].
Sebastopol: O'Reilly Media, 2020.
|
| [14] |
CHEN Y J, LI L, LI W, et al. Chapter 3-deep learning, AI computing systems: An application driven perspective[M].
San Francisco: Morgan Kaufmann, 2023.
|
| [15] |
张洋铭, 万定生. 改进PSO-LSTM的水文时间序列预测[J]. 计算机工程与设计, 2022, 43(1): 203-209. ZHANG Yangming, WAN Dingsheng. Hydrological time series prediction based on improved PSO-LSTM[J]. Computer Engineering and Design, 2022, 43(1): 203-209. |
| [16] |
ZHANG L, HUANG Y W, XUAN J, et al. Trust evaluation model based on PSO and LSTM for huge information environments[J].
Chinese Journal of Electronics, 2021, 30(1): 92-101.
DOI:10.1049/cje.2020.12.005 |
| [17] |
杨维, 李歧强. 粒子群优化算法综述[J]. 中国工程科学, 2004(5): 87-94. YANG Wei, LI Qiqiang. Survey on partical swarm optimization algorithm[J]. Engineering Science, 2004(5): 87-94. |
| [18] |
胡旺, 李志蜀. 一种更简化而高效的粒子群优化算法[J]. 软件学报, 2007, 18(4): 861-868. HU Wang, LI Zhishu. A simpler and more effective partical swarm optimization algorithm[J]. Journal of Software, 2007, 18(4): 861-868. |
| [19] |
李岩, 刘鑫月, 乔俊杰, 等. 基于数据预处理和Bi-LSTM的智能电网预测方法[J]. 电测与仪表, 2025, 62(6): 120-125. LI Yan, LIU Xinyue, QIAO Junjie, et al. Smart grid forecasting method based on data preprocessing and Bi-LSTM[J]. Electrical Measurement & Instrumentation, 2025, 62(6): 120-125. |
| [20] |
CHEN Q, HUANG M X. Rough fuzzy model based feature discretization in intelligent data preprocess[J/OL]. Journal of Cloud Computing, 2021, 10: 5. (2021-01-18)[2023-04-22]. https://doi.org/10.1186/s13677-020-00216-4.
|
 2025, Vol. 42
2025, Vol. 42



 ,
,