扩展功能
文章信息
- 邵文平, 冯静安, 祁登亮, 张峰, 蔺元刚.
- SHAO Wenping, FENG Jing'an, QI Dengliang, ZHANG Feng, LIN Yuangang
- 基于最大相关熵无迹卡尔曼滤波的车辆状态观测
- Vehicle state observation with unscented Kalman filtering based on maximum correntropy
- 公路交通科技, 2025, 42(9): 27-36
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(9): 27-36
- 10.3969/j.issn.1002-0268.2025.09.003
-
文章历史
- 收稿日期: 2023-12-19
在科技和社会不断演进的背景下,人们对汽车安全性的关注度持续攀升。为了提高行车稳定性并降低事故发生率,改进车辆的主动安全系统至关重要。主动安全系统若要有效运作,必须获取准确的车辆状态数据。然而在实际使用过程中,受限于传感器高昂的价格和测量信号的可靠性,一些重要的车辆状态参数如纵向车速、侧向车速、质心侧偏角以及横摆角速度等无法实现实时测量。因此,利用低成本传感器结合融合估计算法是学者的研究热点[1]。
针对车辆动力学系统状态的估计问题,国内外学者已进行了大量的研究和探索,并提出了多种观测技术。这些技术方案包括Luenberger观测器、递归最小二乘估计[2-3]、卡尔曼滤波(Kalman Filtering, KF)[4-5]、滑模观测器[6-7]以及其他类型的非线性观测器等[8-9]。
非线性观测器与卡尔曼滤波是车辆状态估计中应用较为广泛的方法。尽管非线性观测器在特定情况下能提供较高的估计精度,但其性能易受车辆模型参数不精确性的影响。基于卡尔曼滤波的方法在汽车定位、导航中有着广泛应用[10]。
卡尔曼滤波算法涵盖多种类型,容积卡尔曼滤波(Cubature Kalman Filtering,CKF)适用于线性系统,应用于非线性系统时,其估计精度会大幅降低,甚至可能导致滤波器发散。扩展卡尔曼滤波(Extended Kalman Filtering, EKF)通过对非线性系统在工作点进行局部线性化近似,继而应用CKF算法实现其状态估计。但是在实际应用中,EKF会引入截断误差,使参数的估计难以达到理想的精度;与依赖线性近似的方法不同,无迹卡尔曼滤波(Unscented Kalman Filtering, UKF)利用无迹变换直接处理非线性系统的概率分布,无需计算雅可比矩阵,从而在强非线性条件下展现出更高的估计精度和鲁棒性。考虑到车辆系统普遍具有的强非线性特性,UKF被广泛应用于此类系统的状态估计[11-13]。Song[14]构建了一种基于UKF的四轮独立转向车辆状态观测器。该观测器的估计输出成功应用于车辆底盘控制系统,有效提升了其稳定性。Chen[15]构建了一个基于自适应神经模糊推理系统与无迹卡尔曼滤波融合机制的车辆侧向速度实时估计模型,并将估计结果集成到车辆控制系统中。
卡尔曼滤波的经典形式假定过程噪声与量测噪声均服从高斯分布。实际系统中,随机信号常呈现出非高斯特性。因此,过程噪声和量测噪声的非高斯建模能更好地反映真实工况,对于提高系统辨识和估计的准确性具有重要意义。粒子滤波器(Particle Filtering, PF)是一种适用于非线性、非高斯环境的状态估计算法[16]。为了评估不同滤波器的性能,一项研究[17]比较了UPF、UKF和EKF在车辆关键参数估计上的表现,这些参数包括纵向和横向速度、横摆角速度以及轮胎侧向力。该研究发现,UPF在处理非线性问题时表现出更高的精度。然而,粒子滤波器面临着计算复杂度高以及稳定性和收敛性方面的挑战,这些问题需要进一步研究。
传统的卡尔曼滤波算法依赖于最小均方误差准则,因此在非高斯噪声环境下其性能会受到显著影响。与此不同,相关熵能够提取误差信号的高阶统计信息,为提升信号处理和机器学习算法的性能提供了可能[18]。最大相关熵准则卡尔曼滤波器的提出,有效解决了非高斯噪声环境下的自适应滤波难题,并为提升系统在复杂噪声条件下的整体估计性能提供了新的途径[19-20]。
本研究针对非高斯噪声环境中车辆状态估计精度和鲁棒性下降的问题,提出一种基于最大相关熵准则的无迹卡尔曼滤波算法,推导最大相关熵无迹卡尔曼滤波算法(MCUKF)。通过联合仿真,验证双移线工况和正弦波转向输入工况下MCUKF算法的可靠性。
1 车辆动力学模型 1.1 三自由度车辆动力学模型在传统二自由度车辆模型的基础上,考虑算法的实时性以及车辆模型的准确性,本研究所建立的车辆模型为三自由度模型,包括纵向、侧向和横摆3个方向,如图 1所示。
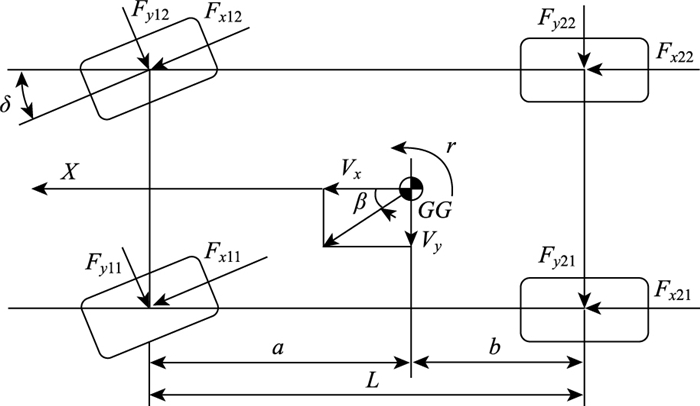
|
| 图 1 整车3自由度模型简图 Fig. 1 Three-degree-of-freedom model of vehicle |
| |
针对所建立的三自由度车辆模型,作如下假设:
(1) 假设车辆结构对称,做平面运动,忽略侧倾、俯仰运动及运动之间的耦合。
(2) 假定车辆悬架系统只作垂向运动,忽略转向传动机构对前轮转角的影响。
纵向平衡方程:
| $ \begin{gathered} m a_x=\left(F_{x 11}+F_{x 12}\right) \cos \delta- \\ \left(F_{y 11}+F_{y 12}\right) \sin \delta+\left(F_{x 21}+F_{x 22}\right) 。\end{gathered} $ | (1) |
侧向平衡方程:
| $ \begin{gathered} m a_y=\left(F_{x 11}+F_{x 12}\right) \sin \delta+ \\ \left(F_{y 11}+F_{y 12}\right) \cos \delta+F_{y 21}+F_{y 22} 。\end{gathered} $ | (2) |
绕z轴力矩平衡方程:
| $ \begin{gathered} I_z \cdot \dot{r}=\left[\left(F_{x 11}+F_{x 12}\right) \sin \delta+\left(F_{y 11}+F_{y 12}\right) \cos \delta\right] a+ \\ {\left[\left(F_{x 11}+F_{x 12}\right) \cos \delta+\left(F_{y 11}-F_{y 12}\right) \sin \delta\right] \frac{t_{\mathrm{w} 1}}{2}+} \\ \left(F_{x 21}+F_{x 22}\right) \frac{t_{\mathrm{w} 2}}{2}-\left(F_{y 21}+F_{y 22}\right) b, \end{gathered} $ | (3) |
其中:
| $ a_x=\dot{v}_x-v_y \times r, $ | (4) |
| $ a_y=\dot{v}_y+v_x \times r, $ | (5) |
式中,δ为前轮转角;vx, vy为纵向车速、侧向车速;r为横摆角速度;β为质心侧偏角;Fxij,Fyij分别为轮胎纵向力和侧向力;为方便描述,采用下标ij标识车辆的4个轮胎,其中ij=11, 12, 21, 22分别表示左前轮、右前轮、左后轮、右后轮。车辆模型中涉及的其他主要参数包括:整车质量m, 质心到前轴的距离a, 质心到后轴的距离b,轴距L=a+b; 前轮轮距tw1, 后轮轮距tw2, 车辆绕z轴的转动惯量Iz,以及车辆的纵向加速度ax和横向加速度ay。
1.2 轮胎模型轮胎作为地面车辆的典型部件,车辆的力和扭矩通过轮胎传递到道路上,其性能直接影响车辆的动态特性。在目前的研究中,主要是基于轮胎物理特性或者半经验公式的Pacejka模型、Dugoff模型。虽然Pacejka的魔术公式应用广泛,但是需要大量的测试才能获得经验参数。Dugoff轮胎模型没有峰值点,最大值小于魔术公式轮胎模型的最大值。随着滑移率的增加,Dugoff轮胎模型和魔术公式轮胎模型的纵向力之差增大,随着轮胎滑移角的增加,两个模型的侧向力之差增加。鉴于以上原因,本研究采用改进后的Dugoff轮胎模型,如下:
| $ F_{x i j}=C_{x i j} \frac{\tan \alpha_{i j}}{1+\lambda_{i j}} f\left(\sigma_{i j}\right) \varphi_{x i j}, $ | (6) |
| $ F_{y i j}=C_{y i j} \frac{\tan \alpha_{i j}}{1+\lambda_{i j}} f\left(\sigma_{i j}\right) \varphi_{y i j}, $ | (7) |
| $ \sigma_{i j}=\frac{\mu_{i j \max } F_{z i j}\left(1+\lambda_{i j}\right)}{2 \sqrt{\left(C_{x i j} \lambda_{i j}\right)^2+\left(C_{y i j} \tan \alpha_{i j}\right)^2}}, $ | (8) |
| $ \begin{gathered} \phi_{x i j}=\left(1.15-0.75 \mu_{i j \max }\right) \lambda_{i j}^2- \\ \left(1.63-0.75 \mu_{i j \max }\right) \lambda_{i j}+1.27, \end{gathered} $ | (9) |
| $ \varphi_{y i j}=\left(-1.6+\mu_{i j \max }\right) \tan \alpha_{i j}+1.155, $ | (10) |
| $ f\left(\sigma_{i j}\right)=\left\{\begin{array}{l} \sigma_{i j}\left(2-\sigma_{i j}\right)&\left(\sigma_{i j} \leqslant 1\right) \\ 1 &\left(\sigma_{i j}>1\right), \end{array}\right. $ | (11) |
| $ \lambda_{i j}=\frac{R \omega_{i j}-V_x}{\max \left(R \omega_{i j}, V_x\right)}, $ | (12) |
式中,Cxij和Cyij分别为纵向和侧向侧偏刚度;μijmax为路面峰值附着系数;ϕxij和φyij分别为轮胎的纵向和侧向修正系数;λij为滑移率;αij为轮胎侧偏角。
轮胎侧向力和侧偏角的计算与垂向载荷有关,计算公式可参考文献[11]。
2 车辆状态观测器设计 2.1 系统状态方程与量测方程采用状态空间方程的形式来描述非线性系统的状态估计模型:
| $ \dot{x}(t)=f(x(t), u(t))+w(t), $ | (13) |
| $ y(t)=h(x(t), u(t))+v(t), $ | (14) |
式中w(t),v(t)分别为过程噪声和测量噪声,互不相关且均值为零。
由以上描述的车辆动力学方程,定义系统的状态变量为
在进行车辆状态观测器的设计时,需要对状态方程进行离散,离散形式为:x(t+1)=F(x(t), u(t)),本研究采用一阶欧拉法进行离散:
| $ \left\{\begin{array}{l} v_x(t+1)=v_x(t)+f_1 \Delta t \\ v_y(t+1)=v_y(t)+f_2 \Delta t \\ r(t+1)=r(t)+f_3 \Delta t \end{array}\right., $ | (15) |
其中,
| $ \begin{gathered} f_1=\left[\left(F_{x 11}+F_{x 12}\right) \cos \delta-\left(F_{y 11}+F_{y 12}\right)\right. \\ \left.\sin \delta+\left(F_{x 21}+F_{x 22}\right)\right] / m-v_y \times r, \\ f_2=\left[\left(F_{x 11}+F_{x 12}\right) \sin \delta+\left(F_{y 11}+F_{y 12}\right) \cos \delta+\right. \\ \left.F_{y 21}+F_{y 22}\right] / m+v_x \times r, \\ f_3=\left[\left(F_{x 11}+F_{x 12}\right) \sin \delta+\left(F_{y 11}+F_{y 12}\right) \cos \delta\right] a+ \\ {\left[\left(F_{x 11}+F_{x 12}\right) \cos \delta+\left(F_{y 11}-F_{y 12}\right) \sin \delta\right] \frac{t_{\mathrm{w} 1}}{2}+} \\ \left.F_{x 21}+F_{x 22}\right) \frac{t_{\mathrm{w} 2}}{2}-\left(F_{y 21}+F_{y 22}\right) b / I_z, \end{gathered} $ |
系统输入为:
| $ u=(\delta) \text { 。} $ | (16) |
上述推导结合MCUKF算法,即可进行车辆状态观测器的设计。
2.2 最大相关熵准则考虑两个随机变量X和Y,以FXY(x, y)表示它们的联合分布函数。两者之间的相关熵定义如下:
| $ V(X, Y)=E[\kappa(X, Y)]=\int \kappa(x, y) \mathrm{d} F_{X Y}(x, y), $ | (17) |
式中,E为期望算符,κ(·, ·)为满足Mercer条件的核函数,通常情况下κ(·, ·)为一个高斯核函数:
| $ \kappa(x, y)=G_\sigma(e)=\exp \left(-\frac{e^2}{2 \sigma^2}\right), $ | (18) |
式中,e=x-y;σ为核宽度,且σ>0。
假设
| $ \hat{V}(X, Y)=\frac{1}{n} \sum\limits_{i=1}^n \exp \left(-\frac{e(i)^2}{2 \sigma^2}\right) 。$ | (19) |
式中,
经过泰勒级数展开,高斯核函数可用于构建基于最大相关熵准则的代价函数,其表达式为:
| $ \max J_{\mathrm{MCC}}=\max \frac{1}{N} \sum\limits_{i=1}^N G_\sigma(e(i)) 。$ | (20) |
高斯相关熵包含了经核宽度σ加权的X和Y的偶阶矩信息。适当选取核宽度,可使信号处理算法能够捕捉并利用高阶矩,从而更准确地描述非高斯分布的特性。
2.3 最大相关熵无迹卡尔曼滤波算法最大相关熵无迹卡尔曼滤波算法MCUKF是一种基于最大相关熵准则的UKF框架下的新算法,可以更好地处理非线性系统中的非高斯噪声。
非线性离散时间系统模型为:
| $ \left\{\begin{array}{l} x(k+1)=f(k, x(k))+w(k) \\ y(k+1)=h(x(k+1))+v(k+1) \end{array}\right., $ | (21) |
式中, w(k)和v(k)分别为相互不相关的过程噪声和测量噪声; Q(k)和R(k)分别为两者的协方差矩阵。
首先,根据UT变换获得一组Sigma点集:
| $ \begin{gathered} \chi^0(k \mid k)=\hat{\boldsymbol{x}}(k \mid k), \\ \chi^1(k \mid k)=\hat{\boldsymbol{x}}(k \mid k)+(\sqrt{(n+\lambda) \boldsymbol{P}(k \mid k)})_i \\ i=1 \sim n ; \\ \chi^i(k \mid k)=\hat{\boldsymbol{x}}(k \mid k)-(\sqrt{(n+\lambda) \boldsymbol{P}(k \mid k)})_{i-n} \\ i=n+1 \sim 2 n \end{gathered} $ | (22) |
计算2n+1个Sigma点集:
| $ \chi^{(i)}(k+1 \mid k)=\boldsymbol{f}\left(k, \chi^i(k \mid k)\right) \quad i=0 \sim 2 n。$ | (23) |
由式(23)及Sigma点权值可得系统状态量的一步预测及协方差矩阵为:
| $ \hat{\boldsymbol{x}}(k+1 \mid k)=\sum\limits_{i=0}^{2 n} \omega_{\mathrm{m}}^i \chi^{(i)}(k+1 \mid k), $ | (24) |
| $ \begin{gathered} \boldsymbol{P}(k+1 \mid k)=\sum\limits_{i=0}^{2 n} \omega_{\mathrm{c}}^i\left[\hat{\boldsymbol{x}}(k+1 \mid k)-\chi^{(i)}(k+1 \mid k)\right]\cdot \\ {\left[\hat{\boldsymbol{x}}(k+1 \mid k)-\chi^{(i)}(k+1 \mid k)\right]^{\mathrm{T}}+\boldsymbol{Q}(k),} \end{gathered} $ | (25) |
式中,ωm,ωc为采样点对应的权值, 然后根据上一步预测值,产生新的Sigma点集:
| $ \begin{aligned} & \chi^0(k+1 \mid k)=\hat{\boldsymbol{x}}(k+1 \mid k) \\ & \chi^i(k+1 \mid k)=\hat{\boldsymbol{x}}(k+1 \mid k)+(\sqrt{(n+\lambda) \boldsymbol{P}(k+1 \mid k)})_i \\ & \quad i=1 \sim n, \\ & \chi^i(k+1 \mid k)=\hat{\boldsymbol{x}}(k+1 \mid k)-(\sqrt{(n+\lambda) \boldsymbol{P}(k+1 \mid k)})_{i-n} \\ & \quad i=n+1 \sim 2 n_{\circ} \end{aligned} $ | (26) |
将预测的新Sigma点集代入观测方程,得到相应的观测Sigma点集:
| $ Z^i(k+1 \mid k)=\boldsymbol{h}\left(\chi^i(k+1 \mid k)\right) \text { 。} $ | (27) |
通过上面推导得出以下的非线性模型:
| $ \begin{gathered} {\left[\begin{array}{c} \hat{\boldsymbol{x}}(k+1 \mid k) \\ \boldsymbol{y}(k+1) \end{array}\right]=\left[\begin{array}{c} \boldsymbol{x}(k+1) \\ \boldsymbol{h}(k+1, \boldsymbol{x}(k+1)) \end{array}\right]+} \\ {\left[\begin{array}{c} \eta(\boldsymbol{x}(k+1)) \\ v(k+1) \end{array}\right]}。\end{gathered} $ | (28) |
通过Cholesky分解处理式(25)所描述的协方差矩阵P(k+1|k)和R(k+1)的联合矩阵ψ(k+1):
| $ \begin{gathered} \boldsymbol{\psi}(k+1)=\left[\begin{array}{cc} \boldsymbol{P}(k+1 \mid k) & 0 \\ 0 & \boldsymbol{R}(k+1) \end{array}\right]= \\ \boldsymbol{T}(k+1) \boldsymbol{T}^{\mathrm{T}}(k+1), \end{gathered} $ | (29) |
| $ \boldsymbol{D}(k+1)=\boldsymbol{T}^{-1}(k+1)\left[\begin{array}{c} \hat{\boldsymbol{x}}(k+1 \mid k) \\ \boldsymbol{y}(k+1) \end{array}\right], $ | (30) |
| $ g(\boldsymbol{x}(k+1))=\boldsymbol{T}^{-1}(k+1)\left[\begin{array}{c} \boldsymbol{x}(k+1) \\ h(\boldsymbol{x}(k+1)) \end{array}\right], $ | (31) |
| $ \boldsymbol{e}(k+1)=\boldsymbol{T}^{-1}(k+1)\left[\begin{array}{c} \eta(\boldsymbol{x}(k+1)) \\ \boldsymbol{r}(k+1) \end{array}\right], $ |
| $ e_i(k+1)=d_i(k+1)-g_i[\boldsymbol{x}(k+1)] \text { 。} $ | (32) |
基于互相关熵的代价函数为:
| $ J(k+1)=\sum\limits_{i=1}^{n+m} G_\sigma\left\{d_i(k+1)-g_i[\boldsymbol{x}(k+1)]\right\}, $ | (33) |
式中,di(·)和gi(·)各自代表向量D(·)和g(·)的第i个元素;向量D(·)的维度为m+n。鉴于相关熵的特性,当目标函数取得最大值时,即可获得状态的最优估计,从而得到修正后的协方差矩阵:
| $ \begin{gathered} \boldsymbol{\psi}(k+1)=\boldsymbol{T}(k+1) \boldsymbol{C}^{-1}(k+1) \boldsymbol{T}^{\mathrm{T}}(k+1)= \\ \operatorname{diag}\left(\tilde{\psi}_x(k+1), \boldsymbol{\psi}_y(k+1)\right), \end{gathered} $ | (34) |
| $ \begin{gathered} \boldsymbol{C}(k+1)=\operatorname{diag}\left(G _ { \sigma } \left(e_1(k+1), \cdots,\right.\right. \\ \left.G_\sigma\left(e_{n+m}(k+1)\right)\right)。\end{gathered} $ | (35) |
修正后的观测协方差为:
| $ \boldsymbol{R}(k+1)=\boldsymbol{\psi}_y(k+1) \text { 。} $ | (36) |
由此可推导得到系统观测的先验均值和协方差为:
| $ \hat{y}(k+1 \mid k)=\sum\limits_{i=0}^{2 n} \omega_m^i Z^i(k+1 \mid k), $ | (37) |
| $ \begin{gathered} \boldsymbol{P}_{y_{k+1} y_{k+1}}=\sum\limits_{i=0}^{2 n} \omega_{\rm c}^i\left[Z^i(k+1 \mid k)-\hat{\boldsymbol{y}}(k+1 \mid k)\right] \times \\ {\left[Z^i(k+1 \mid k)-\hat{\boldsymbol{y}}(k+1 \mid k)\right]^{\mathrm{T}}+\boldsymbol{R}(k+1) 。} \end{gathered} $ | (38) |
协方差矩阵和卡尔曼增益矩阵为:
| $ \begin{gathered} \boldsymbol{P}_{x_{k+1} y_{k+1}}=\sum\limits_{i=0}^{2 n} \omega_c^i\left[\chi^i(k+1 \mid k)-\hat{\boldsymbol{x}}(k+1 \mid k)\right] \times \\ {\left[Z^i(k+1 \mid k)-\hat{\boldsymbol{y}}(k+1 \mid k)\right]^{\mathrm{T}}} \\ \boldsymbol{K}(k+1)=\boldsymbol{P}_{x_{k+1} y_{k+1}} \boldsymbol{P}_{y_{k+1}{}^{y}{}_{k+1}}{ }。\end{gathered} $ | (39) |
更新状态估计及协方差:
| $ \begin{gathered} \hat{\boldsymbol{x}}(k+1 \mid k+1)=\hat{\boldsymbol{x}}(k+1 \mid k)+ \\ \boldsymbol{K}(k+1)[\boldsymbol{y}(k+1)-\hat{\boldsymbol{y}}(k+1 \mid k)] \\ \boldsymbol{P}(k+1 \mid k+1)=\boldsymbol{P}(k+1 \mid k)- \\ \boldsymbol{K}(k+1) \boldsymbol{P}_{y_{k+1} y_{k+1}} \boldsymbol{K}^{\mathrm{T}}(k+1) 。\end{gathered} $ | (40) |
本研究采用的车辆状态估计框架如图 2所示。

|
| 图 2 车辆状态估计的MCUKF算法框架 Fig. 2 MCUKF algorithm for vehicle state estimation |
| |
3 仿真验证
本研究采用CarSim与Simulink联合仿真,以验证所提出的MCUKF算法在车辆状态估计中的可行性和有效性,CarSim软件和Simulink模块之间通过S函数模块进行通信。假设惯性测量单元(IMU)安装在车辆的质心处,车辆系统各部分的参数如表 1所示。
| 车辆参数 | 数值 |
| 簧上质量ms/kg | 1 270 |
| 簧下质量mus/kg | 142 |
| 车辆总质量m/kg | 1 412 |
| 质心高度hg/m | 0.54 |
| 前后轴到质心的距离(a, b)/m | 1.101 5/1.895 |
| 横摆转动惯量Izz/(kg·m―2) | 1 536.7 |
| 前轮侧偏刚度C1/(N·rad―1) | ―148 900 |
| 后轮侧偏刚度C2/(N·rad―1) | ―82 200 |
由于传感器噪声影响算法的协方差矩阵,本研究假设传感器噪声为非高斯噪声。同时,陀螺仪和侧向加速度也存在噪声,且认为传感器噪声都为非高斯噪声。
本研究假设过程噪声与量测噪声均为厚尾分布,并建模为混合高斯分布,具体形式如下:
| $ \begin{aligned} & \left\{\begin{array}{l} Q_{\mathrm{r}}=0.208, w_{k-1, v_x} \sim 0.8 N(0,0.01)+0.2 N(0,1) \\ Q_{v_y}=0.208, w_{k-1, v_x} \sim 0.8 N(0,0.01)+0.2 N(0,1), \\ Q_{v_x}=0.208, w_{k-1, v_x} \sim 0.8 N(0,0.01)+0.2 N(0,1) \end{array}\right. \\ & \left\{\begin{array}{l} R_r=0.208, v_{k, r} \sim 0.8 N(0,0.01)+0.2 N(0,1) \\ R_{a_y}=0.208, v_{k, a_y} \sim 0.8 N(0,0.01)+0.2 N(0,1), \\ R_{a_x}=0.208, v_{k, a_x} \sim 0.8 N(0,0.01)+0.2 N(0,1) \end{array}\right. \end{aligned} $ |
即, Q=diag ([0.208, 0.208, 0.208]),R=diag ([0.208, 0.208, 0.208])。
误差协方差矩阵P初始化为P0=0.01×diag([1,1,1])。最大相关熵准则框架中,核宽度的设置直接影响滤波器的性能表现。较小的核宽度提升鲁棒性和精度,但降低收敛速度;较大的核宽度则反之,加速收敛却可能劣化观测器性能。本研究中,综合考虑精度和收敛性因素,设置核宽度σ=1。
为模拟车辆系统在非线性与非高斯条件下的运行状态,验证所提算法的有效性,并评估其相对于UKF算法的性能,本研究选取双移线工况(100 km/h)与正弦波转向输入(40 km/h)进行仿真试验,并对两种算法的估计结果进行对比分析。为了对仿真结果进行定量分析,采用平均绝对误差(MAE)和均方根误差(RMSE)两项指标对仿真结果进行量化分析。
| $ \begin{gathered} e_{\mathrm{RMS}}=\sqrt{\frac{1}{M} \sum\limits_{k=1}^M\left(x_k-\hat{x}_k\right)^2}, \\ e_{\mathrm{MA}}=\frac{1}{M} \sum\limits_{k=1}^M\left|x_k-\hat{x}_k\right| 。\end{gathered} $ | (41) |
式中, eRMS为RMSE值;eMA为MAE值。
3.1 正弦转向输入工况模拟车辆在附着系数为0.85的路面上行驶,且初始车速设定为40 km/h,并设定初始状态向量为x0= [0, 40/3.6, 0],通过前轮转角输入观测器,并量测纵向加速度、侧向加速度和横摆角速度。各变量的时域响应曲线见图 3。
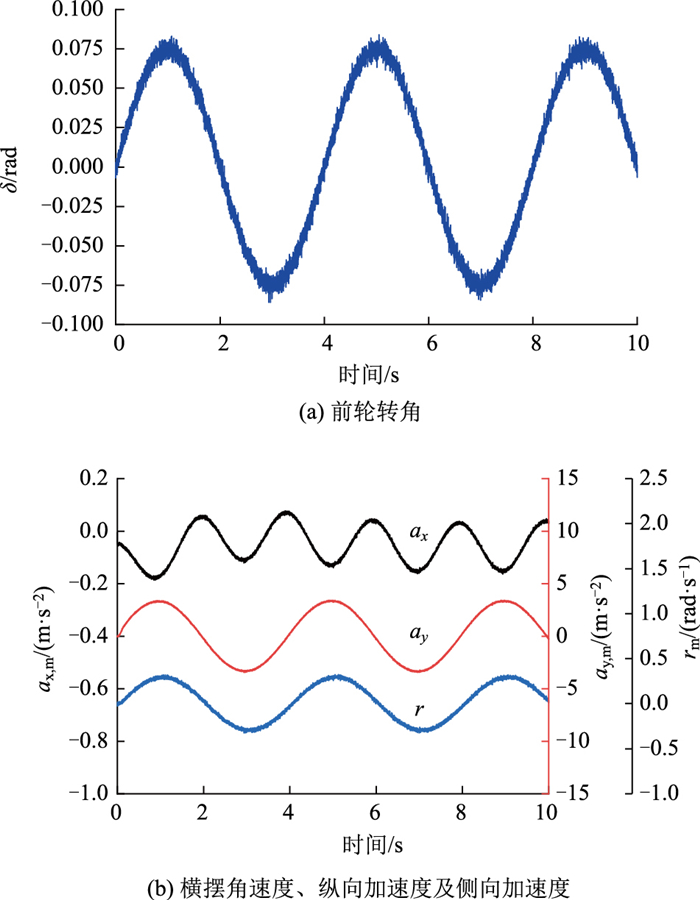
|
| 图 3 正弦转向工况下观测器输入与量测信号 Fig. 3 Observer inputs and measured signals in sine steering condition |
| |
UKF和MCUKF算法在纵向车速、侧向车速和横摆角速度估计方面的性能表现及其估计误差如图 4所示。表 2总结了两种算法的RMSE值和MAE值性能指标。
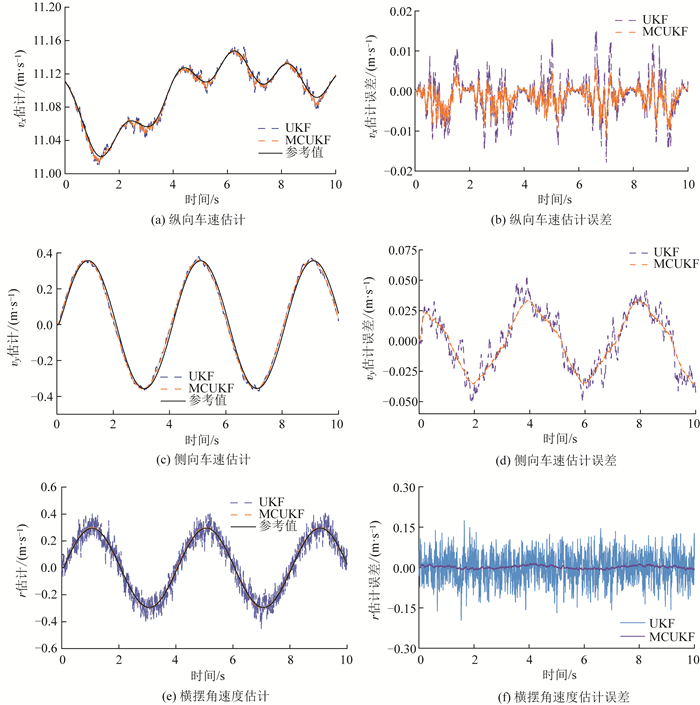
|
| 图 4 正弦输入工况下纵向车速、侧向车速、横摆角速度的估计结果与估计误差 Fig. 4 Estimation results and errors of longitudinal vehicle speed, lateral vehicle speed and yaw rate in sine input condition |
| |
| 指标 | 估计对象 | UKF算法 | MCUKF算法 |
| RMSE值 | vx | 0.004 7 | 0.002 9 |
| vy | 0.024 7 | 0.021 6 | |
| r | 0.046 6 | 0.005 7 | |
| MAE值 | vx | 0.003 4 | 0.002 1 |
| vy | 0.022 2 | 0.019 6 | |
| r | 0.039 2 | 0.004 8 |
图 4(a),4(b)为纵向车速估计结果,其中UKF估计的最大绝对误差达到0.015 m/s,而MCUKF的最大绝对误差为0.008 m/s波动小;由表 2可知,相比于UKF,MCUKF的估计精度提高38%。非高斯噪声环境下,UKF和MCUKF算法对侧向车速的估计均出现波动,结果见图 4(c)和4(d)。UKF算法的峰值误差超过0.06 m/s,而MCUKF算法的估计值与真实值更为吻合,表现出更优的估计精度。
图 4 (e),4(f)为横摆角速度估计结果,由图可知,UKF的估计结果波动大,车辆转弯时出现较大误差,与真实值之间相差较大。UKF算法最大绝对误差达到0.16 rad/s,而MCUKF算法最大绝对误差仅为0.02 rad/s。高速转弯过程中,车辆横摆角速度的快速变化导致传感器数据中出现大量离群点。这种非高斯噪声的存在,使得标准UKF算法难以获得理想的估计效果。MCUKF算法在收敛性上表现更佳,能够有效逼近真实值。而UKF算法则受到非高斯噪声的显著影响,导致其收敛性下降。由表 2可知,MCUKF算法的均方根误差和平均绝对误差均小于UKF算法估计,表示其估计结果精度更高。
综上所述,在正弦转向输入工况下,MCUKF算法对非高斯噪声具有很强的抑制作用,算法的收敛性和跟踪性能较好,表现出高估计精度和强鲁棒性。
3.2 双移线工况仿真分析模拟车辆在附着系数为0.85的路面上行驶,且初始车速设定为100 km/h,并设定初始状态向量为x0= [0, 100/3.6, 0],通过前轮转角输入观测器,并量测纵向加速度、侧向加速度和横摆角速度。各变量的时域响应曲线见图 5。
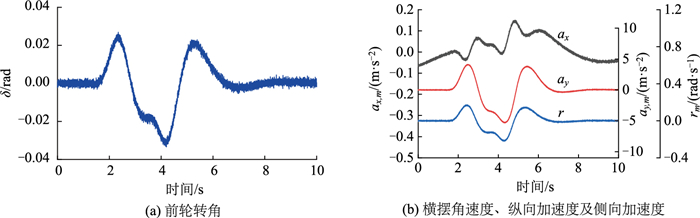
|
| 图 5 双移线工况下状态观测器的输入和量测 Fig. 5 Observer inputs and measured signals in double line condition |
| |
图 6展示了UKF和MCUKF两种算法在纵向车速、侧向车速及横摆角速度方面的估计效果及其误差分布,而表 3则列出了两种算法的均方根误差(RMSE)和平均绝对误差(MAE)量化指标。
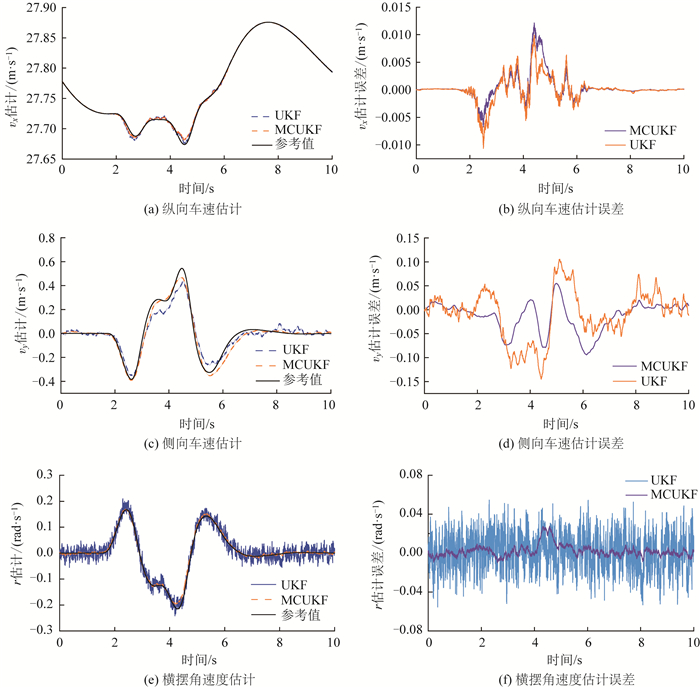
|
| 图 6 双移线输入工况下纵向车速、侧向车速、横摆角速度的估计结果与估计误差 Fig. 6 Estimation results and errors of longitudinal vehicle speed, lateral vehicle speed and yaw rate in double line input condition |
| |
| 指标 | 估计对象 | UKF | MCUKF |
| RMSE值 | vx | 0.002 9 | 0.002 4 |
| vy | 0.050 7 | 0.036 4 | |
| r | 0.018 3 | 0.006 5 | |
| MAE值 | vx | 0.001 5 | 0.001 2 |
| vy | 0.042 2 | 0.024 9 | |
| r | 0.015 2 | 0.004 3 |
图 6(a)和6(b)展示了两种算法对纵向车速的估计性能。结果表明,UKF算法的最大绝对误差达到了0.013 m/s,而MCUKF算法则表现出更强的鲁棒性,其最大绝对误差不超过0.01 m/s。针对非线性观测问题,UKF算法依赖于无迹变换(UT)选取Sigma点,并假设状态变量服从高斯分布。当观测噪声偏离高斯分布时,该算法的估计精度会显著下降。车辆在转弯工况下,状态变量发生剧烈改变,传感器数据更易出现异常值,非高斯噪声的影响更为显著,进而降低UKF算法的跟踪能力。如图 6(c)和6(d)所示,受非高斯噪声影响,UKF算法难以准确估计车辆的侧向速度,试验结果表明,估计值的波动性明显增加,并伴随显著的峰值误差。对于横摆角速度的估计(如图 6(e)和6(f)所示),UKF算法的最大绝对误差达到0.06 rad/s,而MCUKF算法的最大绝对误差不超过0.03 rad/s,表明MCUKF算法的估计精度相比UKF算法提高了64%。
同样的,由表 3可知,MCUKF算法的均方根误差和平均绝对误差均小于UKF算法估计,表示其估计结果精度更高。MCUKF算法相较于UKF算法,能够更有效地抑制非高斯噪声的干扰,从而在收敛速度、跟踪精度、状态估计精度和系统鲁棒性等方面表现出更优越的性能;但MCUKF算法仍存在算法复杂度高,调优过程比较复杂,计算成本高等问题。
综上所述,本研究所提出的车辆状态观测器能够对纵向车速、侧向车速及横摆角速度进行有效的估计,且估计结果与Carsim参考值具有较高的一致性,证明了该观测器在车辆状态估计中的有效性。
4 结论(1) 本研究提出了一种改进的无迹卡尔曼滤波(UKF)算法,该算法融合了最大相关熵准则,旨在提升非高斯噪声环境下车辆行驶状态估计的准确性,建立了三自由度车辆模型,设计了车辆状态观测器。通过仿真试验,将MCUKF估计值、UKF估计值和参考值进行对比。
(2) 两种典型工况下仿真结果表明,MCUKF算法的估计结果更加接近参考值;估计结果的均方根误差表明MCUKF算法的估计误差和波动更小。相比于UKF算法,MCUKF算法能够更好地抑制非高斯噪声,收敛性和跟踪性能更好,具有更高的估计精度和更强的鲁棒性。
(3) 本研究提出的MCUKF算法可以抑制传感器中的非高斯噪声,估计结果具有较高的精度,能够有效地估计车辆的纵向速度、侧向速度、横摆角速度等车辆状态,在非高斯环境下表现出较强的鲁棒性,但也存在算法复杂度高,需要克服计算量的问题。此算法具有较好的工程应用前景和价值,也可为后续汽车状态参数观测系统设计提供理论借鉴。但由于试验条件的限制,未能将所提出的算法应用于实际,进行实车试验,在以后的工作中,有望将所提出的算法应用到实车试验上。
| [1] |
施泽, 方留杨, 张春香, 等. 高速公路风光储融合系统优化配置及经济运行方法[J]. 公路交通科技, 2025, 42(1): 10-21. SHI Ze, FANG Liuyang, ZHANG Chunxiang, et al. Optimization configuration and economical operation method for expressway wind-photovoltaic-energy storage integration system[J]. Journal of Highway and Transportation Research and Development, 2025, 42(1): 10-21. DOI:10.3969/j.issn.1002-0268.2025.01.002 |
| [2] |
CHOI M, OH J J, CHOI S B. Linearized recursive least squares methods for real-time identification of tire-road friction coefficient[J].
IEEE Transactions on Vehicular Technology, 2013, 62(7): 2906-2918.
|
| [3] |
KIM C S, HAHN J O, HONG K S, et al. Estimation of tire-road frictionbased on onboard 6-DoF acceleration measurement[J].
IEEE Transactions on Vehicular Technology, 2014, 64(8): 3368-3377.
|
| [4] |
GADOLA M, CHINDAMO D, ROMANO M, et al. Development and validation of a Kalman filter-based model for vehicle slip angle estimation[J].
Vehicle System Dynamics, 2014, 52(1): 68-84.
|
| [5] |
JUNG H, CHOI S B. Real-time individual tire force estimation for an all-wheel drive vehicle[J].
IEEE Transactions on Vehicular Technology, 2017, 67(4): 2934-2944.
|
| [6] |
陈倩, 孙健, 潘承晨, 等. 城市过饱和区域积分终端滑模控制算法[J]. 公路交通科技, 2025, 42(1): 1-9. CHEN Qian, SUN Jian, PAN Chengchen, et al. Integral terminal sliding mode control algorithm for urban oversaturated regions[J]. Journal of Highway and Transportation Research and Development, 2025, 42(1): 1-9. DOI:10.3969/j.issn.1002-0268.2025.01.001 |
| [7] |
程瑞芬, 魏鑫磊, 夏海英. 基于车辆安全配置的道路运输车辆运行安全风险评估[J]. 公路交通科技, 2023, 40(5): 193-201. CHENG Ruifen, WEI Xinlei, XIA Haiying. Evaluation on operational safety risk of road transport vehicles based on vehicle safety configuration[J]. Journal of Highway and Transportation Research and Development, 2023, 40(5): 193-201. DOI:10.3969/j.issn.1002-0268.2023.05.026 |
| [8] |
GAO Xiaojie, YU Zhuoping, NEUBECK J, et al. Sideslip angle estimation based on input-output linearisation with tire-road friction adaptation[J].
Vehicle System Dynamics, 2010, 48(2): 217-234.
|
| [9] |
HASHEMI E, ZARRINGHALAM R, KHAJEPOUR A, et al. Real-time estimation of the road bank and grade angles with unknown input observers[J].
Vehicle System Dynamics, 2017, 55(5): 648-667.
|
| [10] |
陈慧, 高博麟, 徐帆. 车辆质心侧偏角估计综述[J]. 机械工程学报, 2013, 49(24): 76-94. CHEN Hui, GAO Bolin, XU Fan. Review on vehicle sideslip angle estimation[J]. Journal of Mechanical Engineering, 2013, 49(24): 76-94. |
| [11] |
宋义彤, 舒红宇, 陈仙宝, 等. 分布式电动汽车状态与参数无迹卡尔曼滤波估计[J]. 机械工程学报, 2020, 56(16): 204-213. SONG Yitong, SHU Hongyu, CHEN Xianbao, et al. State and parameters estimation for distributed drive electric vehicle based on unscented Kalman filter[J]. Journal of Mechanical Engineering, 2020, 56(16): 204-213. |
| [12] |
KIM J. Identification of lateral tyre force dynamicsusing an extended Kalman filter from experimentalroad test data[J].
Control Engineering, 2009, 17(3): 357-367.
|
| [13] |
BOADA B L, BOADA M J L, DIAZ V. Vehicle sideslip angle measurement based on sensor datafusion using an integrated ANFIS and an unscented Kalman filter algorithm[J].
Mechanical Systems 8.Signal Processing, 2016, 72-73: 832-845.
|
| [14] |
SONG Y T, SHU H Y, CHEN X B. Chassis integrated control or 4WIS distributed drive EVs with model predictive control based on the UKF observer[J].
Science China Technological Sciences, 2020, 63(3): 397-409.
|
| [15] |
CHEN Z X, DUAN Y P, ZHANG Y Q. Automated vehicle path planning and trajectory tracking control based on unscented Kalman filter vehicle state observer[J/OL]. SAE Report, 2021. (2021-06-04)[2025-02-19]. https://doi.org/10.4271/2021-01-0337.
|
| [16] |
CHEN J, CHENG L, GAN M G. Extension of SGMF using Gaussian sum approximation for nonlinear/non-Gaussian model and its application in multipath estimation[J].
Acta Automatica Sinica, 2013, 39(1): 1-10.
|
| [17] |
CHU W B, LUO Y G, DAI Y F, et al. Vehicle state estimation for in-wheel motor electric vehicle using unscented particle filter[J].
International Journal of Vehicle Design, 2015, 67(2): 115-136.
|
| [18] |
LÜ S H, ZHAO H Q, ZHOU L J. Maximum mixture total correntropy adaptive filtering against impulsive noises[J].
Signal Processing, 2021, 189: 108236.
DOI:10.1016/j.sigpro.2021.108236 |
| [19] |
XU B, WANG X Y, ZHANG J, et al. Maximum correntropy delay Kalman filter for SINS/USBL integrated navigation[J].
ISA transactions, 2021, 117: 274-287.
|
| [20] |
QI D L, FENG J G, WAN W K, et al. A novel maximum correntropy adaptive extended Kalman filter for vehicle state estimation under non-Gaussian noise[J].
Measurement Science and Technology, 2023, 34: 025114.
DOI:10.1088/1361-6501/aca172 |
 2025, Vol. 42
2025, Vol. 42



 ,
,