扩展功能
文章信息
- 邓祥辉, 胡子兆, 王靖媛, 王睿.
- DENG Xianghui, HU Zizhao, WANG Jingyuan, WANG Rui
- 考虑界面影响的隧道爆破峰值振速预测模型
- Peak vibration velocity prediction model for tunnel blasting considering interface effects
- 公路交通科技, 2025, 42(9): 176-182
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(9): 176-182
- 10.3969/j.issn.1002-0268.2025.09.018
-
文章历史
- 收稿日期: 2023-04-27
2. 西安市军民两用土木工程测试技术与毁损分析重点实验室, 陕西 西安 710021
2. Xi'an Key Laboratory of Civil Engineering Testing and Destruction Analysis on Military-Civil Dual Use Technology, Xi'an, Shaanxi 710021, China
在隧道爆破施工过程中,对相邻建筑物产生的振动影响是不可避免的,很多情况下导致邻近建筑物的损伤和破坏。关于爆破振动对相邻建筑物产生的影响,国内外学者进行了深入研究,并取得了一些成果[1-4]。在爆破施工对建筑物安全评价方面,很多学者认为爆破振动速度能够评估爆破振动对相邻建筑物的影响。因此,计算分析质点爆破振动速度就显得尤为重要[5-6]。
目前,确定爆破振动速度的方法主要有两种:一是现场测试,二是经验公式预测。关于这两方面,很多学者进行了研究。张光权[7]以放马峪铁矿为例,利用爆破现场所测数据,运用回归分析法拟合出金属矿山台阶爆破振动预测公式。肖黎[8]利用ALE流固耦合算法求出所需结构动力学等问题的控制方程,并模拟出了建筑物在爆破荷载下的破坏过程。陈文宇[9]以深圳地铁某车站基坑开挖为例,针对基坑爆破对周围建筑物振动响应进行研究,得到了炸药在爆炸过程中建筑物会出现最大振动响应,然后渐渐趋于稳定。孙金山[10]以利用应力波理论和力学模型,分析了在爆破作用下产生的瑞利波在岩体内的响应特征。胡学龙[11]依据露天矿山台阶爆破为例,研究地质条件对地震波传播途径的影响,并提出了基于等效路径的质点振速表达式。朱俊[12]以溪洛渡水电站导流洞开挖为例,根据爆破参数,运用LS-DYNA软件对隧道岩体爆破开挖过程进行响应计算,得到峰值质点振速和最大拉应力的统计关系。
根据现有研究,施工爆破所产生的应力波是导致建筑物发生振动响应的根本原因。应力波的传播不仅与爆破源的能量大小相关,还与应力波传播介质密切相关。当前关于爆破应力波传播和振动速度的研究很少考虑介质界面对应力波传递的影响。因此在本研究中,运用应力波传播与衰减理论,考虑不同界面转换时入射角和反射角度的影响,结合现场测试方法,研究考虑界面影响的质点爆破峰值振动速度理论计算公式,对于研究爆破振动对相邻建筑物的影响至关重要。
1 考虑界面影响的质点振动速度理论公式对于相邻建筑物的爆破振动问题,应力波在具有显著差异的介质界面处的传播过程是不容忽视的。首先认为界面小范围区域内为弹性体;利用弹性固体中波传播规律的力学理论对应力波在界面处的传播进行分析;考虑应力波与界面的相互作用,提出考虑界面影响的质点振速理论计算公式[13-15]。
1.1 爆破荷载峰值σ0根据C-J模型理论炮孔壁的初始峰值压力σ0计算公式如下:
| $ \sigma_{0}=\frac{\rho_{0} D_{\mathrm{CJ}}^{2}}{2(\gamma+1)}, $ | (1) |
不耦合装药条件下:
| $ \sigma_{0}=\frac{\rho_{0} D_{\mathrm{CJ}}^{2}}{2(\gamma+1)}\left(\frac{r_{0}}{r_{\mathrm{b}}}\right)^{2 \lambda}, $ | (2) |
式中,σ0为初始峰值应力;ρ0为炸药初始密度;DCJ为爆速;γ为绝热指数;γ0为装药半径;γb为炮孔半径;λ为爆炸绝热膨胀常数,可取为2.1。
当炸药爆炸后,岩体首先会受到冲击波的作用,在传播过程中冲击波会不断衰减直至达到应力波,衰减形式呈指数式衰减,如式(3)所示:
| $ p=\sigma_{\mathrm{r}}=\sigma_{\mathrm{o}} R^{-\alpha} , $ | (3) |
式中,R为比距离,R=r/rb,r为质点距药室中心的距离;σr为径向应力峰值;α为应力波衰减系数。
当冲击波慢慢衰减变为应力波时,应力波随后也会出现同样的衰减规律,不同之处则是衰减系数不一样。相关学者针对衰减系数的研究,发现其与泊松比有着密切联系[16],如式(4)所示:
| $ \alpha=2-\frac{\mu^{\prime}}{1-\mu^{\prime}}, $ | (4) |
式中,μ′为岩石的泊松比。当介质为弹性体,泊松比取0.5,则衰减系数α为1。从式(3)和式(4)可以看出,波在衰减时不仅受传播距离的影响还与泊松比有关。
1.2 P波作用下的质点振动速度根据岩体内应力波的传播理论,其传播速度等于动弹性模量与泊松比、岩石的密度比值,CL纵波传播波速为:
| $ C_{\mathrm{L}}=\sqrt{\frac{E_{\mathrm{d}}\left(1-\mu^{\prime}\right)}{\rho\left(1+\mu^{\prime}\right)\left(1-2 \mu^{\prime}\right)}} 。$ | (5) |
CT横波传播波速为:
| $ C_{\mathrm{T}}=\sqrt{\frac{E_{\mathrm{d}}}{2 \rho\left(1+\mu^{\prime}\right)}}, $ | (6) |
式中,μ′为泊松比;ρ为岩石密度;Ed为动弹性模量。
根据爆炸应力波的传播过程,研究岩体内部因爆破冲击荷载作用下受力情况。当应力作用在波阵面上,并且满足牛顿第三定律和自由面界面连续条件时,岩体内动应力如式(7)所示:
| $ \sigma_{\mathrm{p} i}=C_{\mathrm{L}} \rho v_{\mathrm{p}}, \quad \sigma_{\mathrm{pr}}=R_{0} \sigma_{\mathrm{p} i}, $ | (7) |
式中,vp为质点振速;σpi为入射P波产生的拉应力;σpr为反射P波产生的拉应力;R0为反射系数。
反射系数不仅与振幅有关,还与相位有着密切的联系。因其计算过程繁琐,遂采用简化后的结果[17-18],则反射系数R0的表达式:
| $ R_{0}=\frac{\tan \beta \tan ^{2}(2 \beta)-\tan \alpha}{\tan \beta \tan ^{2}(2 \beta)+\tan \alpha} 。$ | (8) |
综合式(8),得到考虑P波作用下应力与质点振动速度的关系如下:
| $ \begin{align*} v_{\mathrm{p}}(\sigma)= & \frac{\left[\sigma_{\mathrm{r}}\right]\left[\tan \beta \tan ^{2}(2 \beta)+\tan \alpha\right]}{\left[\tan \beta \tan ^{2}(2 \beta)-\tan \alpha\right] \cos \alpha} \cdot \\ & \sqrt{\frac{\left(1+\mu^{\prime}\right)\left(1-2 \mu^{\prime}\right)}{E_{\mathrm{d}}\left(1-\mu^{\prime}\right) \rho}}, \end{align*} $ | (9) |
式中,ρ为岩石密度;μ′为岩石的泊松比;Ed为动弹性模量。
1.3 考虑界面影响的质点爆破峰值振速计算公式将界面小范围区域内视为弹性体,在此前提下,根据波的传播理论、衰减理论以及应力波在界面进行反射和透射的情况,将界面影响的质点振动速度理论公式整合,如式(10)所示:
| $ \left\{\begin{array}{l} \sigma_{\mathrm{o}}=\frac{\rho_{0} D_{\mathrm{CJ}}^{2}}{2(\gamma+1)}\left(\frac{r_{0}}{r_{\mathrm{b}}}\right)^{2 \lambda} \\ \sigma_{\mathrm{r}}=\sigma_{\mathrm{o}}\left(\frac{r}{r_{\mathrm{b}}}\right)^{-\alpha} \\ \begin{gathered} v_{\mathrm{p}}(\sigma)=\frac{\left[\sigma_{\mathrm{r}}\right]\left[\tan \beta \tan ^2(2 \beta)+\tan \alpha\right]}{\left[\tan \beta \tan ^2(2 \beta)-\tan \alpha\right] \cos \alpha} \cdot \\ \sqrt{\frac{\left(1+\mu^{\prime}\right)\left(1-2 \mu^{\prime}\right)}{E_{\mathrm{d}}\left(1-\mu^{\prime}\right) \rho}} \end{gathered} \end{array}\right. 。$ | (10) |
因此,考虑界面影响的质点爆破峰值振速公式为:
| $ \begin{gather*} v=\frac{\left[\frac{\rho_{0} D_{\mathrm{CJ}}^{2}}{2(\gamma+1)}\left(\frac{r_{0}}{r_{\mathrm{b}}}\right)^{2 \lambda} R^{-\alpha}\right]\left[\tan \beta \tan ^{2}(2 \beta)+\tan \alpha\right]}{\left[\tan \beta \tan ^{2}(2 \beta)-\tan \alpha\right] \cos \alpha} . \\ \sqrt{\frac{\left(1+\mu^{\prime}\right)\left(1-2 \mu^{\prime}\right)}{E_{\mathrm{d}}\left(1-\mu^{\prime}\right) \rho}} 。\end{gather*} $ | (11) |
从式(13)可以看出质点峰值振速不仅受到入射角和反射角的影响,还与岩土体性质等密切相关。
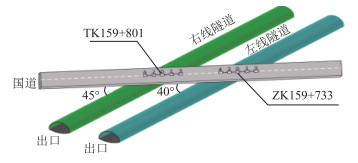
2 工程验证 2.1 工程概况依托工程为宝鸡—汉中高速关林子隧道出口段工程。该隧道围岩为强风化片麻岩,节理裂隙发育,岩体破碎。关林子隧道下穿隧道出口位于G316国道下方,隧道左线ZK159+733与右线YK159+801断面均处于最小埋深。当修建隧道下穿于既有道路时,爆破振动对既有道路会产生影响,尤其当下穿隧道开挖断面大、埋深小时,爆破振动产生的效果更明显。此下穿隧道左线与G361国道呈40°交角,下穿隧道右线与G361国道呈45°交角,两者位置关系如图 1所示。
|
| 图 1 路面监测点布置图 Fig. 1 Layout of road surface monitoring points |
| |
2.2 爆破参数及炮孔布置
爆破参数的选取不仅决定了爆破的效果,还决定了其对周围环境的影响[19-21]。根据施工现场地质条件及炮孔布置情况确定出爆破参数。施工现场岩体属于Ⅴ级围岩,岩体情况差,所以将掏槽孔和辅助孔采用不耦合、反向起爆装药结构;周边孔选用不耦合装药结构。隧道爆破炮孔布置和装药量见表 1和表 2。
| 开挖位置 | 炮孔名称 | 炮孔深度/m | 雷管级别/段 | 炮孔数量/个 | 每孔药量/kg | 合计药量/ kg |
| 上台阶 | 掏槽孔 | 1.2 | 1 | 8 | 0.80 | 6.72 |
| 辅助孔 | 1.0 | 3 | 16 | 0.40 | 6.40 | |
| 辅助孔 | 1.0 | 5 | 6 | 0.40 | 2.40 | |
| 辅助孔 | 1.0 | 7 | 24 | 0.40 | 9.60 | |
| 辅助孔 | 1.0 | 9 | 19 | 0.40 | 7.60 | |
| 周边孔 | 1.0 | 11 | 61 | 0.20 | 13.40 | |
| 底板孔 | 1.0 | 13 | 21 | 0.40 | 8.40 |
| 开挖位置 | 炮孔名称 | 炮孔深度/m | 雷管级别/段 | 炮孔数量/个 | 每孔药量/kg | 合计药量/ kg |
| 下台阶 | 辅助孔 | 1.0 | 1 | 13 | 0.40 | 5.20 |
| 辅助孔 | 1.0 | 3 | 13 | 0.40 | 5.20 | |
| 辅助孔 | 1.0 | 5 | 13 | 0.40 | 5.20 | |
| 辅助孔 | 1.0 | 7 | 9 | 0.40 | 3.60 | |
| 辅助孔 | 1.0 | 9 | 4 | 0.40 | 1.60 | |
| 周边孔 | 1.0 | 11 | 23 | 0.20 | 4.60 | |
| 周边孔 | 1.0 | 13 | 32 | 0.40 | 12.80 |
2.3 路面监测点布置
综合考虑场地的工程地质条件,将最容易发生破损的部位选为监测断面。根据现场施工情况,左线ZK159+733和右线YK159+801断面与既有道路相离最近,于是在这两个断面上方的路面处布置监测点,爆破测试点在每个断面上方共布置5个监测点,对称分部在路面基准点的两侧。本研究主要以右线YK159+801断面上方的监测点为研究对象。爆破振动监测仪器选用TC-4850爆破振动记录仪。
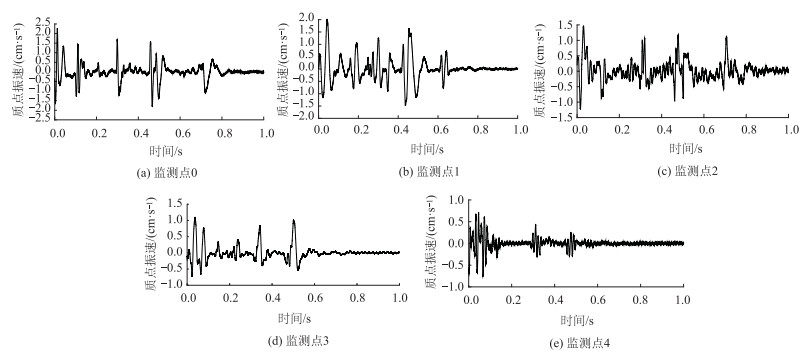
2.4 现场测试以及结果分析将现场实测的振动数据进行汇总,发现Z方向的振速最大,根据规范要求选择振速最大的方向为研究对象,运用Blasting Vibration Analysis软件进行数据处理。提取出YK159+801断面监测点的振速波形变化如图 2所示及各监测点振速及相关参数见表 3。
|
| 图 2 YK159+801断面监测点振动速度图 Fig. 2 Diagrams of vibration velocity of monitoring points at section YK159+801 |
| |
| 测点编号 | 最大振速出现段位 | 最大振速方向 | Z向最大质点振速/ (cm·s―1) | 爆心距/ m |
| 0 | 1段 | Z | 2.35 | 7.49 |
| 1.15 | 12.15 | |||
| 0.67 | 17.25 | |||
| 1 | 1段 | Z | 1.99 | 8.77 |
| 0.91 | 14.22 | |||
| 0.49 | 20.19 | |||
| 2 | 1段 | Z | 1.46 | 10.20 |
| 0.78 | 16.55 | |||
| 0.35 | 23.49 | |||
| 3 | 1段 | Z | 1.19 | 12.63 |
| 0.49 | 20.48 | |||
| 0.29 | 29.08 | |||
| 4 | 1段 | Z | 0.86 | 15.21 |
| 0.39 | 24.67 | |||
| 0.29 | 35.03 |
从图 2波形图可以看出,在0~0.2 s时间区段里,Z方向质点振速最大。在后续时间里,质点振速仍出现多次大幅波动,然后慢慢衰减直至消失;YK159+801断面的爆破振动过程中在监测点0处达到最大质点振速为2.35 cm/s,在监测点4处是最小质点振速为0.29 cm/s。从表 3可以得出距离爆源越远其质点振速越小的规律。在监测过程中质点最大振速为2.35 cm/s,满足设计安全振速小于2.5 cm/s要求。
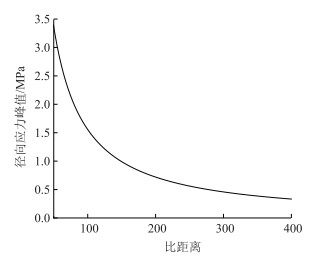
2.5 分析验证此工程选用的是2#岩石乳化炸药,每卷重量200 g;起爆选用8#电雷管;炸药密度为1 g/cm3;爆速为4 000 m/s;炮孔半径为20 mm;装药半径为16 mm,由式(2)计算不耦合装药情况下的初始峰值应力σo,计算求得σo=1.014 GPa。然后由式(3)计算出相应的σr,其中Ⅴ级围岩的衰减系数α为1.46。径向应力σr峰值的变化如图 3所示。从图 3可知,随着比距离继续增大,径向应力峰值将会不断减小直至0 MPa。当路面质点与药室中心相距最近时,对应的比距离为100左右,σr=1.22 MPa,即当σr的范围在0.16~1.22 MPa时符合工程实际。
|
| 图 3 Ⅴ级围岩的径向应力峰值变化 Fig. 3 Radial stress peak variation of surrounding rock class-Ⅴ |
| |
当确定好各监测点中应力波的入射角度时,根据式(11)计算出质点振动速度,然后整合YK159+801断面监测点的理论预测结果与实测结果,如表 4所示。
| 测点编号 | 入射角度数/ (°) | 爆心距/m | 质点峰值振速/(cm·s―1) | |
| 实测值 | 公式预测值 | |||
| 0 | 0 | 7.49 | 2.35 | 2.44 |
| 12.15 | 1.15 | 1.23 | ||
| 17.25 | 0.67 | 0.71 | ||
| 1 | 5 | 8.77 | 1.99 | 1.94 |
| 14.22 | 0.91 | 1.01 | ||
| 20.19 | 0.49 | 0.53 | ||
| 2 | 12 | 10.20 | 1.46 | 1.59 |
| 16.55 | 0.78 | 0.87 | ||
| 23.49 | 0.35 | 0.34 | ||
| 3 | 20 | 12.63 | 1.19 | 1.28 |
| 20.48 | 0.49 | 0.53 | ||
| 29.08 | 0.29 | 0.32 | ||
| 4 | 28 | 15.21 | 0.86 | 0.98 |
| 24.67 | 0.39 | 0.42 | ||
| 35.03 | 0.29 | 0.33 | ||
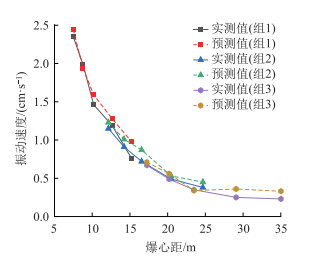
采用本研究提出的理论公式计算可以算出YK159+801断面的爆破振动速度,并与现场实测值进行对比,结果如图 4所示。
|
| 图 4 振动速度对比 Fig. 4 Comparison of vibration velocities |
| |
从图 4可见,现场实测值与理论公式预测值表现出相同的变化趋势,随着爆心距的增大,质点峰值振速不断减小。在埋深较浅入射角度较小时质点峰值振速较大随入射角度增大振速衰减较快。在埋深较大入射角度较大时质点峰值振速较小随入射角增大振速衰减较慢,即质点峰值振速随埋深增大敏感度逐渐降低。爆心距越大,爆破应力波能量衰减越大,其引起的质点振速越小,破坏效应越弱。随埋深增大,爆破应力波入射角度增大爆心距增大时产生的质点峰值振速对邻近建筑物影响不大。同时,由表 4可以看出,质点振动速度的最小值出现在监测点1位置,其中现场实测值为2.35 cm/s,公式预测值为2.44 cm/s,两者相对误差为3.83%;相对误差最大值出现在监测点4位置,实测值为0.29 m/s,公式预测值为0.33 cm/s,相对误差为13.79%。通过以上对比分析,发现在理论分析中考虑界面影响的理论公式能够准确反映路面质点的振动速度,说明本研究理论预测公式是具有合理性和可靠性的。
3 结论本研究基于爆破应力波在岩土体介质中的传播理论,推导了考虑界面影响的质点爆破峰值振速公式,并在宝鸡-汉中高速关林子隧道下穿国道出口段进行了工程验证。主要结论如下:
(1) 隧道爆破开挖过程中,应力波在岩土体介质传播中受不同界面影响,在考虑不同界面转换时入射角和反射角角度的影响,推导了质点爆破峰值振速计算公式。
(2) 通过对关键测点的现场监测,可以看出采用理论公式预测与实测得到的监测点振动速度规律基本一致,即质点振速均呈现出随爆源距离的增加而逐渐减小的趋势。
(3) 从现场测试的质点峰值振速和理论公式预测的相对误差分析可见,本研究提出的理论公式预测值与实测值平均误差为8.21%,表明本研究提出的理论公式能较好反映爆破应力波在不同介质传播的规律,也能比较准确地预测质点振动速度。
| [1] |
张袁娟, 孔德增. 不同岩性对爆破振动效应影响研究[J]. 矿冶工程, 2019, 39(5): 6-8. ZHANG Yuanjuan, KONG Dezeng. Influence of different lithology on blasting vibration effect[J]. Mining and Metallurgical Engineering, 2019, 39(5): 6-8. |
| [2] |
XIE L X, LU W B, GU J C, et al. Excavation method of reducing blasting vibration in complicated geological conditions[J].
Shock and Vibration, 2018(1): 2518209.
DOI:10.1155/2018/2518209 |
| [3] |
王学斌. 公路隧道施工对邻近建筑物的影响及控制[J]. 公路交通科技, 2022, 39(8): 182-190. WANG Xuebin. Influence and control of highway tunnel construction on adjacent buildings[J]. Journal of Highway and Transportation Research and Development, 2022, 39(8): 182-190. DOI:10.3969/j.issn.1002-0268.2022.08.024 |
| [4] |
王晓星, 张昱辉, 鲁彪. 机械与爆破法下路基开挖对既有临近隧道的影响[J]. 公路交通科技, 2022, 39(4): 101-107. WANG Xiaoxing, ZHANG Yuhui, LU Biao. Influence of excavating roadbed by mechanical and blasting methods on existing adjacent tunnel[J]. Journal of Highway and Transportation Research and Development, 2022, 39(4): 101-107. DOI:10.3969/j.issn.1002-0268.2022.04.011 |
| [5] |
闫鹏, 张云鹏, 申宇宙, 等. 爆破振动作用下建筑物动力响应研究综述[J]. 金属矿山, 2025(6): 131-143. YAN Peng, ZHANG Yunpeng, SHEN Yuzhou, et al. Review on the dynamic response of buildings subjected to blasting vibration[J]. Metal Mine, 2025(6): 131-143. |
| [6] |
王栋, 何历超, 王凯. 钻爆法施工对邻近埋地管道影响的现场实测与数值模拟分析[J]. 土木工程学报, 2017, 50(增2): 134-140. WANG Dong, HE Lichao, WANG Kai. Field measurement and numerical simulation for influence of blasting excavation on adjacent buried pipelines[J]. China Civil Engineering Journal, 2017, 50(S2): 134-140. |
| [7] |
张光权, 吴春平, 施俊健, 等. 金属矿山台阶爆破振速预测研究[J]. 中国矿业, 2012, 21(5): 101-104. ZHANG Guangquan, WU Chunping, SHI Junjian, et al. Research on the forecasting of blasting vibration by bench blasting in metal mining[J]. China Mining Industry, 2012, 21(5): 101-104. |
| [8] |
肖黎, 屈文忠, 余杰. 建筑物内爆流固耦合数值分析[J]. 武汉理工大学学报, 2009, 31(10): 56-59. XIAO Li, QU Wenzhong, YU Jie. Numerical studies on solid-fluid interaction in building implosion[J]. Journal of Wuhan University of Technology, 2009, 31(10): 56-59. |
| [9] |
陈文宇, 张云, 陈行, 等. 基坑爆破施工对邻近建筑物的动力响应[J]. 科学技术与工程, 2018, 18(23): 281-287. CHEN Wenyu, ZHANG Yun, CHEN Xing, et al. Study on dynamic response of foundation pit blasting construction to adjacent buildings[J]. Science Technology and Engineering, 2018, 18(23): 281-287. |
| [10] |
孙金山, 李正川, 刘贵应, 等. 爆破振动在边坡岩土介质中诱发的动应力与振动特征分析[J]. 振动与冲击, 2018, 37(10): 141-148. SUN Jinshan, LI Zhengchuan, LIU Guiying, et al. Dynamic stress and vibration characteristics of geomaterials in slopes induced by blasting vibration[J]. Journal of Vibration and Shock, 2018, 37(10): 141-148. |
| [11] |
胡学龙, 璩世杰, 蒋文利, 等. 基于等效路径的爆破地震波衰减规律[J]. 爆炸与冲击, 2017, 37(6): 966-975. HU Xuelong, QU Shijie, JIANG Wenli, et al. Attenuation law of blasting seismic waves based on equivalent paths[J]. Explosion and Shock Waves, 2017, 37(6): 966-975. |
| [12] |
朱俊, 杨建华, 卢文波, 等. 地应力影响下隧洞边墙的爆破振动安全[J]. 爆炸与冲击, 2014, 34(2): 153-160. ZHU Jun, YANG Jianhua, LU Wenbo, et al. Safety of blasting vibration of tunnel sidewall under the influence of ground stress[J]. Explosion and Shock Wave, 2014, 34(2): 153-160. |
| [13] |
雷振, 李卓, 雷兴海, 等. 爆破振动作用下高层建筑振速变化规律研究[J]. 工程爆破, 2022, 28(2): 7-14. LEI Zhen, LI Zhuo, LEI Xinghai, et al. Variation law of vibration velocity of high-rise buildings under blasting vibration[J]. Engineering Blasting, 2022, 28(2): 7-14. |
| [14] |
邓祥辉, 王靖媛, 杨俊, 等. 地铁隧道爆破施工影响的邻近居民楼质点峰值振速研究[J]. 地震工程学报, 2022, 44(1): 17-21, 45. DENG Xianghui, WANG Jingyuan, YANG Jun, et al. Peak particle velocity of adjacent residential buildings influenced by blasting construction of subway tunnel[J]. China Earthquake Engineering Journal, 2022, 44(1): 17-21, 45. |
| [15] |
胡其志, 唐益新, 卢国兴. 钻爆法施工对软硬围岩过渡段振动特性研究[J]. 地下空间与工程学报, 2020, 16(增1): 201-207. HU Qizhi, TANG Yixin, LU Guoxing. Study on the vibration characteristics of soft and hard surrounding rock transition section by drilling and blasting method[J]. Journal of Underground Space and Engineering, 2020, 16(S1): 201-207. |
| [16] |
宋守志. 固体介质中的应力波[M]. 北京: 煤炭工业出版社, 1989. SONG Shouzhi. Stress wave in solid media[M]. Beijing: Coal Industry Press, 1989. |
| [17] |
于亚伦. 工程爆破理论与技术[M]. 北京: 冶金工业出版社, 2004. YU Yalun. Engineering blasting theory and technology[M]. Beijing: Metallurgical Industry Press, 2004. |
| [18] |
陈明, 卢文波. 爆炸应力波对新浇混凝土衬砌的影响研究[J]. 岩土力学, 2008, 146(2): 455-459, 464. CHEN Ming, LU Wenbo. The influence of explosive stress wave on young concrete lining[J]. Rock and Soil Mechanics, 2008, 146(2): 455-459, 464. |
| [19] |
邹宝平, 罗战友, 杨建辉, 等. 基于参数敏感分析的软弱破碎地层大断面隧道爆破质量优化[J]. 科技通报, 2017, 33(2): 143-147. ZOU Baoping, LUO Zhanyou, YANG Jianhui, et al. Quality optimization of blasting in soft fractured rock mass on large cross-section tunnels based on analysis parameter sensitivity[J]. Bulletin of Science and Technology, 2017, 33(2): 143-147. |
| [20] |
李刚. 临海大断面超浅埋公路隧道侧穿敏感建筑物控爆技术[J]. 公路交通科技, 2023, 40(1): 160-168. LI Gang. Controlled blasting technology for shallow-buried large section tunnel side crossing susceptible buildings in coastal stratum[J]. Journal of Highway and Transportation Research and Development, 2023, 40(1): 160-168. DOI:10.3969/j.issn.1002-0268.2023.01.018 |
| [21] |
林豪, 郭洪雨, 兰庆男, 等. 大断面小净距隧道爆破施工合理间距及减振措施[J]. 公路交通科技, 2024, 41(6): 165-172. LI Hao, GUO Hongyu, LAN Qingnan, et al. Reasonable spacing and vibration reduction measure for tunnel blasting with large section and small clear distance[J]. Journal of Highway and Transportation Research and Development, 2024, 41(6): 165-172. DOI:10.3969/j.issn.1002-0268.2024.06.018 |
 2025, Vol. 42
2025, Vol. 42



 ,
,