扩展功能
文章信息
- 朱亮伟, 周学军, 李晓琦, 张佳惠, 唐赛.
- ZHU Liangwei, ZHOU Xuejun, LI Xiaoqi, ZHANG Jiahui, TANG Sai
- 多模态数据驱动的高速公路机电设备寿命预测
- Multi-modal data fusion based expressway electromechanical equipment life prediction
- 公路交通科技, 2025, 42(9): 12-26
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(9): 12-26
- 10.3969/j.issn.1002-0268.2025.09.002
-
文章历史
- 收稿日期: 2024-08-22
2. 北京中交国通智能交通系统技术有限公司, 北京 100088
2. Beijing GOTEC ITS Technology Co., Ltd., Beijing 100088, China
随着高速公路网络的迅速发展和扩建,高速公路机电设备的可靠性直接关系到交通系统的安全与效率。高速公路上运行的收费系统、交通监控系统、通信系统、供电系统、照明系统、应急救援系统、通风系统等应用系统中的机电设备,是确保道路安全畅通的关键。这些机电设备在复杂的环境下运行,需要应对连续的负载压力和不断变化的环境条件,使得其寿命预测成为一项重要挑战。
传统的设备寿命预测方法多依赖简化的统计模型或基于物理因素的监测,这些方法通常忽略了运行过程中瞬态电压、电流异常及系统日志中关键信息对机电设备寿命的影响,从而在准确性和鲁棒性方面有所欠缺。近年来,深度学习技术在大数据处理和特征提取方面的优势日益凸显,为机电设备剩余使用寿命(RUL)的预测研究提供了新的思路。借助深度神经网络对多源异构数据的自适应学习能力,可以更有效地捕捉机电设备在复杂环境下的退化特征。
基于此,本研究结合深度学习技术,提出了一种新的多模态数据融合框架,并使用在实际工程中收集整理的SW-RUL-DATAS数据集进行训练,以大幅度提升高速公路机电设备寿命预测的精确度和稳定性。然而,在提出“通过创新方法提升机电设备寿命预测的准确性和可靠性”这一目标时,如何量化地评价预测性能和模型的稳健性依然是一个关键问题。为此,本研究在设计试验与模型评估时,明确采用了均方误差(MSE)、均方根误差(RMSE)及平均绝对误差(MAE)等常用的回归型预测指标来衡量模型的准确性,并结合预测结果与实际机电设备故障(或退化)发生时间的对比,评估模型在不同时段、不同环境条件下的可靠性表现。通过这些量化指标,可以清晰地呈现不同方法在预测效果上的差异,也能更直观地展示多模态数据融合和深度学习模型带来的性能提升。
本研究的主要目标是通过多模态数据融合方法,提高高速公路机电设备寿命预测的准确性和可靠性,并以MSE,RMSE,MAE等指标进行量化评估;采用基于循环神经网络(RNN)的深度学习框架,对瞬态电压、电流、温度、湿度和系统日志等不同数据源的特征进行综合建模,以实现更精准的寿命预测。本研究的主要贡献如下。
(1) 构建了用于高速公路机电设备寿命预测的数据集SW-RUL-DATAS。数据涵盖瞬态电压/电流波形、环境温湿度、设备操作记录与系统日志等多模态异构信息,汇集某路段全生命周期设备数据,为该方向的后续研究提供了宝贵的行业基准与数据支撑。
(2) 构建了一个多尺度的多模态融合的深度学习模型。设计并创新实现了一种基于RNN的多尺度多模态融合的深度学习模型,该模型融合多种模态且频率迥异的数据特征,输入RNN来预测机电设备的剩余使用寿命,模型会使用自动机器学习(AutoML)技术来优化超参数。
(3) 开创了跟踪融合电力应力变化。采用温度湿度应力变化和人为操作应力变化的数据对机电设备寿命影响的模型来预测机电设备寿命的方法,通过消融试验进一步揭示了瞬态电压和电流在机电设备寿命预测中的重要性,证实这些因素对预测性能有显著影响。
1 研究现状作为工业机电设备预防性维护的关键技术,机电设备寿命预测主要通过分析数据预测机电设备故障时间,为智能运维提供决策支持。随着技术的发展,机电设备寿命预测经历了从统计模型、物理模型到机器学习与深度学习的逐步演变。
1.1 传统方法传统的机电设备寿命预测方法包括统计模型和基于物理的模型。
1.1.1 统计模型常用的统计模型包括自回归积分滑动平均(ARIMA)模型和生存分析模型(Kaplan-Meier)。ARIMA模型通过分析历史数据中的趋势和季节性变化,为机电设备寿命预测提供基线模型,在数据结构相对简单、线性关系较明显的场景下有着良好表现[1-10]。例如,杨艺[1]利用ARIMA模型对某类机电设备的寿命进行了预测。但在高速公路机电设备的实际运行环境中,数据通常存在强非线性和高噪声,诸如交通流量的周期性波动、突发性超载运行、瞬态电压电流的大幅波动及温湿度的急剧变化等。这些因素共同作用,使得高速公路机电设备的运行数据呈现出复杂、非平稳的动态特征。当监测机电设备的时序数据出现剧烈波动或非平稳性时,ARIMA模型在预测时会出现模型残差较大、对突发故障前期信号不敏感等问题;在对机电设备寿命进行中长期预测时,模型也可能出现过度平滑或无法捕捉故障征兆的现象,难以及时警示机电设备的潜在退化风险,从而导致效果不佳。Kaplan-Meier则是一种常见的非参数生存分析方法,能够计算机电设备的生存概率和失效分布,适用于无完整故障时间记录或部分缺失故障数据的场合。文昌俊[2]在机电设备生存期研究中曾用此方法估计机电设备故障概率。然而,Kaplan-Meier同样主要适用于相对静态或仅有少量特征变量的场景,难以应对高速公路机电设备多维度、多模态的动态数据需求。在面临大量传感器信息及复杂干扰因素时,Kaplan-Meier缺乏对高维特征关联的捕捉能力。总体而言,统计模型在处理非线性和多模态数据方面能力有限,难以适应高速公路机电设备所处的复杂环境及动态变化,因而在更高精度和实时性需求的寿命预测中逐渐暴露出不足。
1.1.2 物理模型物理模型通过研究机电设备的失效物理特性来推断其寿命,常用方法包括Weibull分布模型及基于失效物理(Physics of Failure, PoF)的模型。这些方法在已知物理特性或故障模式相对明确的机电设备中表现出色。例如,文昌俊[2]通过Weibull分布对机电设备的可靠性进行了分析,能较好地刻画该类机电设备的失效概率分布[11-15]。但是,高速公路机电设备通常在配置、材料特性、使用环境等方面存在很大差异,故障机理也更加多样,且数据缺失情况时有发生,导致基于单一失效物理假设的模型难以适用。此外,机电设备在高速公路场景中所受的负载压力、环境应力通常呈现显著的随机性和时变性,无法用固定的失效规律或退化曲线简单描述,从而进一步削弱了此类物理模型的泛化能力[16-17]。
1.2 机器学习与深度学习随着数据采集和计算能力的不断提升,研究者开始引入机器学习和深度学习方法,以克服统计模型和物理模型的局限。深度学习能够通过大量样本进行特征自动提取,尤其擅长于非线性、高维度、多模态的数据分析,因此在高速公路机电设备寿命预测领域展现了更广阔的应用前景。通过结合多模态数据源(如瞬态电压、电流、环境温湿度、文本日志等),深度学习模型有潜力更全面地捕捉复杂退化过程中的关键特征,为机电设备寿命预测提供更精准的决策支持[18-19]。
然而,对于高速公路机电设备这类数据量大、实时性要求高、环境因素复杂多变的场合,仍需进一步探讨各类方法所面临的挑战和不足。
1.2.1 机器学习方法支持向量机(SVM)、决策树和集成学习方法(如随机森林和梯度提升机)已被应用于寿命预测。利用SVM预测机电设备健康状态;谢楠[4]使用随机森林对机电设备剩余寿命进行建模。这些方法在小规模、单一模态或特征维度相对有限的场景中性能突出。然而,在高速公路机电设备寿命预测中,通常需要应对以下挑战[3, 12, 20-24]。
(1) 数据规模与实时性
高速公路机电设备布点多,运行时间长,所产生的数据量庞大且更新速度快。SVM等传统方法在面对海量数据时,训练过程可能因内存占用和计算复杂度迅速攀升而无法及时迭代;随机森林和梯度提升机等集成学习方法在数据量极大的情况下,训练时间和预测时延同样可能难以满足实时监测需求。
(2) 多模态数据融合
高速公路机电设备的健康状况取决于多种信息源,如瞬态电压电流、环境温湿度、日志信息,以及海拔、粉尘、盐雾等外部因素。SVM和随机森林等方法在高维度或异构数据融合时,通常需要手动特征工程或拆分-组合策略,难以自动化地从多模态数据中获取深层特征交互关系,导致预测精度受限。
(3) 环境因素干扰与噪声
由于高速公路环境中温湿度、负载冲击的非线性变化频繁且波动较大,传统机器学习模型在处理强噪声、高度非平稳数据时稳定性可能有所不足,需要针对外部环境动态特征进行反复调参或复杂的预处理。
1.2.2 深度学习方法深度学习方法(如CNN,RNN,LSTM)因其非线性建模能力在机电设备寿命预测中显示出优势。Qu[5]应用CNN提取信号特征进行故障检测;徐先峰[6]利用LSTM处理时间序列数据进行机电设备寿命预测。尽管如此,深度学习在高速公路机电设备寿命预测场景下仍存在以下几方面挑战。
(1) 高质量数据依赖与多模态融合瓶颈
在高质量数据依赖方面,深度网络在训练中需要大量、相对干净的标注数据。然而,高速公路机电设备可能存在多种传感器故障或测量噪声,数据缺失、异常值及标签不均衡等问题普遍存在,直接影响模型的训练效果和泛化能力。另一方面,多模态融合存在瓶颈,虽然CNN和RNN可以分别处理图像或序列数据,但在同时面对环境数据、瞬态电压电流波形、文本日志等异构信息时,模型结构通常需要定制化设计,若没有合理的融合策略,网络结构复杂度和计算成本都将显著增加。
(2) 计算成本高且实时性要求严苛
在模型训练阶段,深度神经网络包含大量参数,在对海量时间序列及多模态数据进行训练时,需要占用高算力及显存,训练周期较长。若频繁更新模型(如在边缘部署实时自适应模型),其计算成本可能难以符合高速公路现场的硬件条件。在推理阶段,在高速公路机电设备寿命预测中,实时性是关键指标。当需要在边缘或本地服务器进行在线推理时,大规模深度网络推理速度可能无法满足毫秒级或秒级的响应要求,进而影响预警与维护调度的时效性。
(3) 环境因素复杂导致的数据分布偏移
高速公路场景下,气候、负载、路况等环境干扰随季节、天气和交通流量的变化而显著波动。这些因素带来的数据分布动态变化,会降低深度学习模型在部署后的稳健性与可靠性。一旦实际运行环境与模型训练数据出现较大偏差,模型可能出现预测不准确或误报等问题,需要周期性地重新训练或在模型结构中引入自适应机制。
1.3 现有挑战和研究空白尽管机电设备寿命预测技术已取得显著进展,但仍面临多个挑战和研究空白。获取高质量数据仍是主要问题之一[7],尤其是在实际运行环境中,数据常受噪声影响且可能缺乏标签。大多数现有方法依赖大量历史故障数据,对于新机电设备或少见故障模式,这些方法不够有效。此外,多模态数据的有效融合仍是一个未充分解决的问题。一方面,在各种资源有限的情况下,选取采集哪些数据来分析机电设备的剩余寿命能达到综合效率最好,是一个需要研究的问题;另一方面,这些数据的时间和空间异构性,数据模态不一,也给数据融合和分析带来挑战。
面对高速公路机电设备寿命预测所面临的挑战,本研究着力设计一个多尺度的多模态数据融合的深度学习模型,借助机电设备运行环境的温湿度、电压电流瞬时波动状态数据、机电设备运行状态、维护历史等历史数据,对机电设备剩余使用寿命进行预测。考虑到在多模态数据环境中,数据的异构性和采集的资源限制,本研究将探索如何选择最具代表性和影响力的数据,以达到最优的综合预测效果。此外,还将研究多模态数据融合技术,以解决不同数据源在时间和空间上的不一致性问题,确保数据集成过程的高效性和准确性。
2 研究方法 2.1 模型概述多尺寸多模态时序数据融合预测模型的整体流程与关键组件如图 1所示。输入层由3类数据构成:其一为以高采样率获取的瞬态电压/电流波形,用于刻画短时脉冲与非平稳扰动;其二为按固定时间窗聚合的环境温度与相对湿度,用于表征外部工况的平稳与周期性变化;其三为由维护记录与系统日志编码得到的语义向量,用于补充事件与上下文信息。各模态先完成去噪、标准化与时间对齐,并在各自支路内进行多尺度特征提取。电气支路通过频域或时频域与卷积建模获取秒、分钟、小时尺度特征,环境支路提取窗口统计与趋势量,本研究中的维护记录支路获得上下文的语义表示。随后,模型采用分支编码-共享瓶颈的自编码融合结构在统一表示空间内完成跨模态对齐与降维,得到紧凑的融合表示;该表示被送入序列预测层(例如循环神经网络或基于注意力的时序模型),输出设备剩余寿命估计及故障风险评分。训练阶段使用重构损失与预测损失的联合目标并配合正则化以提升稳健性;推理阶段支持按设备与时间窗的在线更新,从而实现对高速公路机电设备的实时预警与寿命预测。
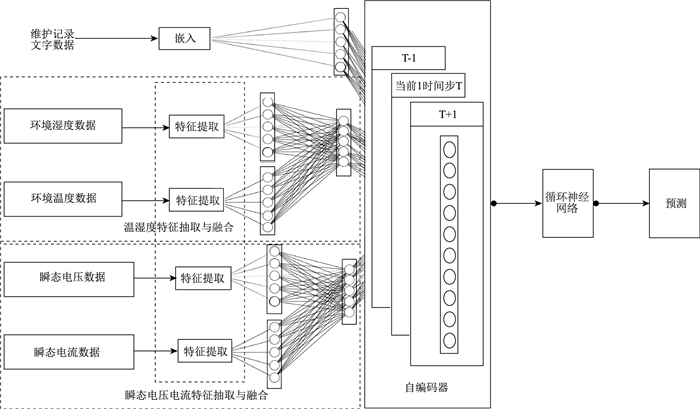
|
| 图 1 多尺寸多模态时序数据融合预测模型架构 Fig. 1 Architecture of multi-scale and multi-modal temporal sequence data fusion prediction model |
| |
多尺寸多模态时序数据融合预测模型是一个综合性的多模态数据处理架构,分为3个主要部分。首先,模型对不同模态的数据进行特征抽取和嵌入:温湿度数据和瞬态电压与电流数据分别通过适应其采集频率的卷积方法进行处理,维护记录的文本数据则通过文本向量化技术进行特征提取。第2部分涉及特征融合,通过自编码模块将同一时间维度上的不同特征融合成统一的编码,随后传递给后续的处理模块。最后,模型通过RNN处理这些融合后的序列数据,专注于长序列数据的预测任务。具体来说,RNN在每个时间步都会接收融合后的特征向量,并结合其上一时刻的隐藏状态来更新当前隐藏状态,以此捕捉不同模态信息随时间演化的动态变化。随后,模型可在最后一个时间步或在一段预测窗口后,将RNN的隐藏状态输入至全连接层或其他预测子模块,用于评估机电设备剩余寿命等长期预测任务。RNN通过这种方式不仅利用其内部循环结构维护并迭代更新序列状态,还能在不同时间步充分整合各模态特征,从而生成更加精确的寿命预测结果。
2.2 数据收集和与预处理 2.2.1 数据源和类型在本研究中,数据的收集涉及多个方面,主要包括通过传感器和数据记录系统获得的机电设备历史性能数据。这些数据包括但不限于温度、湿度、电流、电压等参数,以及机电设备的运行时间和操作状态。这些数据通常以时间序列的形式进行记录,并包含关键环境因素,如温度、湿度等,本研究重点之一是研究瞬态电压电流对机电设备寿命的影响,瞬态电压电流通过特殊电信号采集器来采集,采集频率为20 kHz;温湿度的采集通过温湿度传感器,采样间隔约为5 min/条;维护记录和机电设备日志数据来自原系统运行过程中收集的机电设备相关数据。为保证各数据源在时序与标识维度上的一致性,所有数据在进入建模流程前均完成去重、缺失与异常处理,并统一时区与时间格式,随后按照设备标识与时间轴进行对齐与索引。基于固定时间窗构造样本单元,使同一设备在同一时间窗内的瞬态波形片段、环境统计量与文本向量可以形成时空一致的多模态输入。经由上述流程汇集的数据构成SW-RUL-DATAS数据集,其全部样本均来源于真实的在运营场景。
2.2.2 数据清洗和标准化在将数据输入模型处理前,会有一个数据预处理过程,以确保数据质量和可用性。本研究在此阶段重点进行了缺失值处理、异常值处理及数据标准化处理。
(1) 缺失值处理
本研究主要采用时间序列数据的平均值插值方法,即对于每个有缺失值的时间点,计算其前后时间点的平均值,并用此值填补缺失值。该方法实现简单,可在一定程度上保留时间序列的平滑特性。然而,在实际应用中,如果缺失值所处时段的数据波动较大或存在突变,这种线性插值可能无法准确反映真实趋势。此外,当连续多个时间点都存在缺失时,单纯采用平均值插值可能会带来较大误差。因此,在更复杂或高频的工业场景下,也可考虑其他插值或估计方法(如基于局部多项式拟合的插值、卡尔曼滤波法或基于深度学习的插值模型等),并根据具体数据特征和业务需求进行比较和选择。通过缺失值处理、异常值处理及标准化后,关键数据字段更加完整,无严重极端值,且各特征范围统一到[0, 1]或其他适合的区间,为后续的模型训练和评估提供了更干净、更一致的数据输入。
(2) 异常值处理
为了识别并处理异常值(如极端电流、电压或环境指标等),本研究结合了2种常见方法,但在具体使用时也需结合本研究的数据分布与特征加以调整或互补使用。
方法1:四分位距(QIQR)。该方法对偏度较小、分布相对对称的数据更适用;若数据分布呈强偏态或多峰性,则需结合可视化或其他统计指标进一步判断。首先,计算第1四分位数Q1和第3四分位数Q3;然后计算QIQR(见式(1));最后,识别并处理低于Q1-1.5×QIQR或高于Q3+1.5×QIQR的数据点。
| $ Q_{\mathrm{IQR}}=Q_3-Q_{1}。$ | (1) |
方法2:标准分数(Z-Score)。当数据接近正态分布时,Z-Score方法效果较好;若数据偏离正态分布明显,则可考虑使用经过变换后的数据或结合其他稳健的统计指标。首先计算平均值和标准差,然后识别并处理绝对值大于3的Z-Score数据点。在本研究实际数据集中,若观测到某些特征呈现强烈的非正态分布或明显的多峰特征,需适当调小或调大阈值,或联合使用QIQR与Z-Score分析结果,从而更准确地识别并处理异常点。
(3) 数据标准化处理
本研究采用了Min-Max标准化方法,将每个特征数据缩放至[0, 1]区间,其计算公式为:
| $ X_{\text {norm }}=\frac{X-X_{\min }}{X_{\max }-X_{\min }}, $ | (2) |
式中,Xnorm为经Min-Max标准化后得到的新特征值,取值范围0~1;X为原始特征值;Xmin为该特征在所有样本中的最小值;Xmax为该特征在所有样本中的最大值。
这种方法能在特征数值范围较为稳定且无明显离群点时有效增强不同特征间的可比性,并利于后续模型训练。然而,对于离群值敏感或分布差异较大的特征,Min-Max可能会导致部分数据被“挤压”在狭窄区间,从而影响模型对极端值的判别能力。在此情况下,可考虑使用Z-Score标准化或基于中位数和四分位距等方法,并对不同处理方式进行模型性能评估后再选择最优方案。
以3组典型数据为例,说明SW-RUL-DATAS在缺失值填补、异常值修正及归一化后的变化,如表 1所示。处理前,2#数据存在运行时间缺失及相对湿度超限(99%)的情况;3#数据出现电流、电压空值与极端温度(400 ℃)的情况。经插补与校正后,缺失字段被合理填补,异常数值恢复至物理可行区间,数据完整性、一致性与可用性显著提升,为后续特征提取与RUL建模提供可靠基础。
| 数据编号 | 数据采集时间 | 电流/A | 电压/V | 运行时间/h | 操作状态 | 环境温度/℃ | 相对湿度/% | |
| 处理前 | 1# | 2022-10-18 T 11:01:19 | 5 | 220 | 100 | 正常 | 25 | 50 |
| 2# | 2022-10-18 T 11:01:20 | 10 | 230 | 缺失 | 故障 | 25 | 99 | |
| 3# | 2022-10-18 T 11:01:21 | — | — | 100 | 正常 | 400 | 50 | |
| 处理后 | 1# | 2022-10-18 T 11:01:19 | 5.0 | 220 | 100 | 正常 | 25.0 | 50.0 |
| 2# | 2022-10-18 T 11:01:20 | 5.2 | 230 | 100 | 故障 | 25.0 | 56.3 | |
| 3# | 2022-10-18 T 11:01:21 | 5.1 | 220 | 100 | 正常 | 25.2 | 50.0 | |
2.3 特征抽取和初步融合 2.3.1 文本数据特征的抽取
本模型使用BERT模型来处理维护记录和系统日志中的半结构化文本数据。BERT模型能够深入提取文本的语义特征,用于后续的特征融合与推理。首先,使用BERT的分词器将文本拆分为基本的词元(tokens),包括单词、词根、标点等,将文本转换为一系列词元,如x1,x2,…,xn。然后,将这些词元通过嵌入层转换为对应的预训练向量,并加入位置编码以维持词元在序列中的位置信息,得到词嵌入和位置编码后的向量E:
| $ \begin{aligned} & \boldsymbol{E}=\operatorname{Embedding}\left(x_1, x_2, \cdots, x_n\right)+ \\ & \operatorname{PositionEncoding}(0,1, \cdots, n), \end{aligned} $ | (3) |
式中,Embedding函数负责将每个词元映射到一个高维空间的一个点;位置信息编码函数Position Encoding则把词元的位置信息编码,帮助模型理解词元顺序。
接下来把E输入BERT编码层,经过BERT内部的多层transformer,捕捉词元之间的复杂关系,并输出高级特征表示H,H=BERT(E),E是已加位置编码的嵌入向量序列;H是由L层transformer计算得到的同一长度序列,其中每个位置向量已融合全局上下文,故称为上下文化表示。取H在[CLS]位置对应的向量记为z,即z=H[CLS],该向量浓缩整个输入的语义,可直接用于下游融合或分析。
2.3.2 温湿度数据特征抽取与融合对于温度和湿度的数据,本研究选用t=1 h的时间窗口来截取数据,提取特征。之所以选1 h的窗口,主要基于以下考虑。
(1) 在多数机电设备运行或环境监测场景中,1 h通常能平衡短时波动与整体趋势,既能捕捉温湿度快速变化,又不会过多掩盖长期演化规律。
(2) 1 h的时间尺度在设备热湿响应时滞与运维调度粒度之间取得合理折中, 既能覆盖多数设备对环境扰动的通常为数十分钟量级的短时滞后效应,又使统计特征具备足够的样本量与稳健性,同时在计算资源占用与在线推理时延上保持可接受的成本。
(3) 如果应用场景对温湿度数据的关注点更偏向于分钟级或天级,也可相应调整时间窗口至更短或更长,并重新评估其对后续特征抽取及模型性能的影响。
选定时间窗口后,在提取温度与湿度的时序特征时,本研究采用了CNN方法,具体参数配置与数据特点的关联如下。
(1) 卷积核大小(kernel size=3):在1 h窗口内,每分钟采集一个数据点,总计60个数据。设置大小为3的卷积核有助于捕捉短时间段内的局部变化模式,对温湿度可能出现的微小起伏或瞬时变化较为敏感。
(2) 步长(stride=1):保证卷积核以单位步长在序列上移动,避免错过重要的细节信息,也能在不增大参数量的前提下保持较高分辨率。
(3) 填充方式(padding=‘same’):使输出序列长度与输入相同,便于对温度和湿度进行后续拼接和融合,不因边界效应丢失信息。
(4) 卷积核数量(filters=32):设置32个不同卷积核可在一定程度上增大网络的感受野宽度,以捕获温湿度数据在不同时间局部的多样性特征。若后续试验发现温湿度波动更为复杂或呈现多峰特征,可酌情增大卷积核数量。
温湿度数据特征融合的具体操作如下,对于每个60 min的时间窗口W,用xtT和xtH分别代表在时间t的温度和湿度数据点。
(1) 数据截取。将温度和湿度数据分别按60 min的时间窗口进行截取,得到温湿度的初始输入向量为:
| $ \boldsymbol{W}_{\mathrm{T}}=\left[x_t^{\mathrm{T}}, x_{t+5}^{\mathrm{T}}, \cdots, x_{t+55}^{\mathrm{T}}\right], $ | (4) |
| $ \boldsymbol{W}_{\mathrm{H}}=\left[x_t^{\mathrm{H}}, x_{t+5}^{\mathrm{H}}, \cdots, x_{t+55}^{\mathrm{H}}\right], $ | (5) |
式中t为窗口的开始时间;WT为温度初始输入向量;WH为湿度初始输入向量CNN特征提取。采用大小为3、步长为1的卷积核,使用same填充,并设置32个卷积核(通道数为32个),以捕捉时间窗口内温度与湿度的关键模式与趋势。将温度和湿度数据的特征向量合并,以形成一个综合的特征表示,这表示捕捉了2种类型数据的相互作用和独立特性,用作后续autoencode的输入的一部分。
| $ \begin{gathered} \boldsymbol{f}_{\mathrm{H}}=\operatorname{CNN}\left(\boldsymbol{W}_{\mathrm{H}}\right)=\operatorname{Conv} 1 \mathrm{D}(x, k=3, s=1, \\ p=\text { 'same' }, f=32), \end{gathered} $ | (6) |
| $ \begin{gathered} \boldsymbol{f}_{\mathrm{T}}=\operatorname{CNN}\left(\boldsymbol{W}_{\mathrm{T}}\right)=\operatorname{Conv} 1 \mathrm{D}(x, k=3, s=1, \\ p=\text { 'same' }, f=32), \end{gathered} $ | (7) |
| $ \boldsymbol{f}=\boldsymbol{f}_{\mathrm{T}} \oplus \boldsymbol{f}_{\mathrm{H}}, $ | (8) |
式中,fT和fH分别为从温度和湿度数据窗口提取的特征向量;⊕表示特征向量拼接。
(2) 特征融合。
从温度和湿度的时间序列数据中提取和融合重要特征,为后续autoencode模型提供高质量的输入。
2.3.3 瞬态电压电流数据多尺度特征抽取与融合瞬态电压和瞬态电流的采集频率为每秒2万个数据点,为了对齐数据,采用1 h的时间窗口来截取数据,每个小时总共有7 200万个数据点,数据量非常大。提取瞬态电压和瞬态电流的多尺度特征分4步分别把瞬态电压或瞬态电流的统计特征、多尺度高级特征、频域特征等抽取出来。其中多尺度高级特征包括从细微的电压瞬间波动(比如尖峰电压),到中尺度的波形变换(如谐波),和粗粒度的变化(如电压暂降)等特征,最后通过全连接网络把特征连接起来。
(1) 计算窗口内统计特征,对于瞬态电压和瞬态电流,选取特征向量为平均电压μx、电流标准差σx;峰值电流Imax、最小电流Imin、平均电压Uy、电压标准差σy、峰值电压Umax;最小电压Umin、功率因数P、超限次数N(例如电流或电压超过安全阈值的次数)。通过统计得到时间窗口的统计特征F为:
| $ \boldsymbol{F}=\left[\boldsymbol{\mu}_x, \boldsymbol{\sigma}_x, \boldsymbol{I}_{\max }, \boldsymbol{I}_{\min }, \boldsymbol{U}_y, \boldsymbol{\sigma}_y, \boldsymbol{U}_{\max }, \boldsymbol{U}_{\min }, \boldsymbol{P}, \boldsymbol{N}\right]。$ | (9) |
(2) 使用CNN的层次结构来捕获从局部到全局的特征,设计了一个3层卷积来针对不同的时间尺度秒级、分钟级、小时级数据,提取从细到粗的时序特征。以下是具体的设计方法和每一层如何对应到不同的时间尺度。为在不同时间尺度上表征瞬态电压/电流的判别性模式,本研究构建了由3层一维卷积组成的多尺度特征提取器。设输入序列为x。第1层以卷积核长度3、步长1与有效填充(valid)对x进行卷积后接ReLU激活,得到表征短时突变与高频细节的特征A。第2层在A上采用卷积核长度5、步长2与same填充并接ReLU激活,得到更适配中等尺度波动的特征B。第3层在B上采用卷积核长度7、步长2与same填充并接ReLU激活,得到表征长周期趋势与周期性模式的特征C。随后,本研究将多尺度表示A,B,C通过拼接操作融合为综合特征H;在需要时可叠加全连接层以进一步完成特征映射与压缩。
(3) 把数据先通过一个快速傅里叶变换,得到幅度谱和相位谱,然后通过卷积操作得到频域上的特征S。过程描述如下:
首先对瞬态电压与电流的时域信号实施离散傅里叶变换,以完成从时域到频域的映射并获得幅度谱与相位谱。其后对所得谱数据进行归一化处理,并沿通道维度将电压/电流的幅度谱与相位谱进行拼接,从而形成CNN的输入张量。为从频域表示中同时学习局部模式与跨频段的全局依赖关系,本研究构建由2级“卷积-池化”模块与1层全连接层组成的一维CNN。各卷积层采用卷积核长度为3,步长为1,填充方式为same,并以ReLU作为非线性激活函数;各池化层采用最大池化,窗口大小为2,步长为2。网络尾部将特征图展平后输入全连接层,以整合多尺度频域特征并完成特征映射。最终得到的向量s作为瞬态电压与电流的频域表征,用于后续的多模态融合与推理模块。
(4) 综合特征融合。将所有提取的特征(统计特征F,多尺度时域特征H,频域特征S)融合成一个全面的特征向量V(见式(10));分别对瞬态电压VV和瞬态电流VI采用上述步骤,连接2个特征向量成为最终的多尺度特征向量V(见式(11));最后得到一个瞬态电压和电流综合的特征向量V。
| $ \boldsymbol{V}=\operatorname{Concatenate}(\boldsymbol{F}, \boldsymbol{H}, \boldsymbol{S}), $ | (10) |
| $ \boldsymbol{V}=\operatorname{Concatenate}\left(\boldsymbol{V}_{\mathrm{V}}, \boldsymbol{V}_{\mathrm{I}}\right) \text { 。} $ | (11) |
本研究在多模态寿命预测框架中引入自编码模块,用于对不同数据源产生的高维特征进行统一表征、降维压缩与信息融合。该模块通过学习非线性映射,将原始多模态特征压缩为判别性更强的低维表示;在尽量保持信息保真的前提下,减少参数规模并提升计算效率,从而为后续的时序预测模型提供稳定且紧凑的输入。
记维护记录与系统日志经文本编码器得到的嵌入向量为H∈R^{d_H}(本研究取d_H=1 024),记温度与相对湿度在固定时间窗内的统计/拼接向量为f∈R^{d_f},记基于高频采样瞬态波形提取得到的电气特征为V∈R^{d_V}。3类模态在来源、维度与统计性质方面具有显著差异:文本嵌入通常为高维稠密语义表示,环境量多呈平稳且周期性的连续数值分布,而电气特征常带有较大的动态范围与非平稳尖峰。
2.4.1 输入层与特征融合在输入层,自编码模块同时接收H,f,V这3种特征向量。考虑到三者在维度大小、数据类型及分布特征方面的差异,通过特征拼接或叠加的方法进行初步融合:
| $ \boldsymbol{X}_{\text {concat }}=\boldsymbol{H}-\boldsymbol{f}- \boldsymbol{V} \text {, } $ | (12) |
式中‖为拼接操作;Xconcat为易拼接向量。
自编码器的输入首先在模态内完成标准化与尺度对齐,包括数值归一化、时间窗一致化与缺失值处理,随后在模态间进行向量级融合。在融合之前,文本嵌入直接采用预训练编码器的输出,并对数值型特征执行尺度缩放与标准化。上述处理可以避免某一模态在融合后由于量纲或幅值差异而过度主导或被弱化。
2.4.2 编码层(降维与非线性抽取)使用多个全连接层逐步减少特征维度,同时在各层之间引入激活函数(例如ReLU)来增强非线性,提取模态间的关键信息。这些降维层能够在保留重要信息的基础上,减少高维特征,特别是文本嵌入的冗余,同时融合数值型时序特征,为后续预测模型提供更紧凑、更具判别力的表示。
| $ Z_{\text {encoded }}=\operatorname{ReLU}\left[W_2 \operatorname{ReLU}\left(W_1 X_{\text {concat }}+b_1\right)+b_2\right] $ | (13) |
式中,W1,W2为第1层和第2层权重;b1, b2为第1层和第2层偏量。
2.4.3 解码层(重构与特征保留)解码层结构与编码层大体对应,通过逐层增加维度尝试重构原始输入特征。在解码过程中,使用与编码部分类似的激活函数(如ReLU),以尽可能保留原特征的重要信息。对于数值型特征(温湿度与瞬态电压电流),可监测解码后输出与原输入在数值分布及峰值情况上的一致性;对于文本嵌入向量,可重点关注整体的重构误差。
| $ \widehat{X}_{\text {concat }}=\operatorname{ReLU}\left[W_4 \operatorname{ReLU}\left(W_3 Z_{\text {encoded }}+b_3\right)+b_4\right] $ | (14) |
式中,
本模块使用MSE计算输入与输出之间的差异:
| $ L_{\mathrm{MSE}}=\frac{1}{N} \sum\limits_{i=1}^N\left\|X_{\text {concat }}^i-\widehat{X}_{\text {concat }}^i\right\|^2, $ | (15) |
式中,Xconcati为第i个样本的原始输入;
训练完成后,编码端的输出Zencoded即为多模态特征的低维表示,不仅尽量保留了3个模态的关键信息,也有效抑制了高维输入数据中可能存在的噪声或冗余。自编码模块如此的设计初衷在于:(1)信息融合。在同一向量空间中将文本特征与数值型温湿度、瞬态电压电流特征紧密结合。(2)降维与高效。通过降维降低模型参数规模,缩短后续预测的推理时间。(3)兼容性与适应性。不同模态数据在维度和分布上存在差异,自编码器的端到端训练机制能较好地学习到适用于融合的公共子空间。
最终,自编码器得到的低维表示Z会输入到后续的RNN(或其他序列预测网络)中,用于机电设备运行状态的预测、剩余寿命估计等关键任务。相比直接将3个大相径庭的特征向量拼接输入RNN,自编码后的向量通常能更好地提升预测精度与效率。
2.5 循环神经网络模型多尺寸多模态时序数据融合预测模型的核心原理是基于机电设备的实时数据、历史运行数据和其他关键特征来建立预测模型[8]。RNN是一种专门用于处理序列数据的神经网络,由于其独特的循环结构,RNN能够在处理时间序列数据时保持内部状态(记忆),从而在每个时间步考虑到历史信息,这使得RNN非常适合于长序列数据预测任务,如机电设备寿命预测等,因为这些任务通常需要捕捉时间依赖性和动态变化[23]。
为优化RNN的结构与训练配置,构建覆盖结构规模与优化策略的超参数搜索空间:隐藏状态维度取值{32, 64, 128, 256} 以控制状态容量并覆盖从小型到中等规模的模型;网络深度取值{1, 2, 3} 以在表达能力与计算成本之间取得折中;学习率取值{10-4, 10-3, 10-2}用于覆盖常用量级并支撑从粗到细的优化;批大小取值{16, 32, 64} 以平衡吞吐与稳定性;优化器在Adam与SGD之间选择,用于对比自适应动量法与一阶随机梯度法在非凸目标上的收敛特性。在给定计算预算约束下,AutoML框架采用网格搜索、随机搜索或贝叶斯优化在上述空间中生成候选配置,并按照统一训练流程在训练集上拟合对应的RNN。其中,网格搜索枚举离散组合以提供基线下界,随机搜索与贝叶斯优化则通过分布采样或代理模型与采集函数在高维空间中进行更高效的探索。每个候选配置均在验证口径下评估性能,计算MSE,RMSE,MAE等指标并完整记录搜索日志;在采用交叉验证的情形下,针对同一配置执行多折训练并对指标取平均,以降低随机初始化与数据划分带来的方差。模型选择以验证集RMSE最小为主准则,以MSE作为辅助手段检视误差分布特性;确定最优配置后,使用训练集与验证集的合并数据重新拟合模型,并在独立测试集上报告最终MSE与RMSE,以评估在未见数据上的泛化能力;全过程固定随机种子并保存配置与结果以保证可复现性。
AutoML能够在较广的超参数空间内进行系统化搜索与严谨评估, 从而高效获得与数据特征及任务需求匹配的最优模型配置; 同时减少对人工调参的依赖, 在保证预测精度的前提下提升开发与整体表现。
3 试验 3.1 全因素对比试验 3.1.1 数据集描述本研究使用的试验数据集是来自高速公路机电系统自动化运维项目中的真实数据经收集整理清洗后, 形成SW-RUL-DATAS数据集。该数据集数据来源分别为3个不同路段机电设备的数据,把数据集整理成3个分数据集,即SW-RUL-DATAS1,SW-RUL-DATAS2,SW-RUL-DATAS3。每个数据集均包括高速公路用电设备的故障数据及相关运行和维修日志,这些数据涉及电压、电流、温度、湿度、品牌、维修养护等多种时序数据。在这3个数据集上测试模型的性能和效果。
每个数据集具体分为3部分:(1)养护维修数据集,包含约9万个机电设备的从2017至2022年的维修养护记录,总计约为10万条数据。(2)温湿度数据集,以5 min/条的频率采集的温度和湿度数据。(3)电压电流数据集,使用20 kHz频率采集器收集的电压、电流和电力负载数据。
3.1.2 基线和性能评价指标本模型选取当前典型的4种寿命预测模型Kaplan-Meier,PF-ARIMA[9],CNN+GRU[8],CNN-LSTM[10]做为基线模型。从高速公路机电设备寿命预测的角度来看,这4种模型涵盖了传统统计学方法(Kaplan-Meier)、经典时间序列模型(ARIMA系列)及深度学习模型(CNN+GRU,CNN-LSTM),既具有一定的通用性,又具备在工业机电设备寿命预测领域的代表性。同时,这些模型也各自存在一定局限性,例如对多模态数据融合不够灵活或对非线性关系的刻画仍需进一步挖掘。因此,将这4种方法纳入基线比较,全面评估本研究所提出模型在不同层面的性能提升情况。
本研究主要使用MSE和RMSE指标进行模型性能评估,分别记为式(16)和式(17)。在回归任务中,MSE通常用作损失函数,模型训练的目标是最小化这个值。
| $ L_{\mathrm{MSE}}=\frac{1}{n} \sum\limits_{i=1}^n\left|\widehat{y_i}-y_i\right|, $ | (16) |
式中,LMSE为MSE指标值;yi为预测值;
| $ L_{\mathrm{RMSE}}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(\widehat{y_i}-y_i\right)^2} 。$ | (17) |
式中LRMSE为样本的RMSE指标值。
3.1.3 实现细节全部试验基于PyTorch实现,并在2块NVIDIA A100(80GB)GPU上运行。为获得更优的预测性能,采用AutoML对循环神经网络的超参数进行系统化搜索。在预设的搜索空间内执行训练-验证循环,以验证集指标为准则选择最优组合并保证可复现性。最终确定的RNN配置为:隐藏层数为3,每层神经元数为150个,激活函数为tanh,学习率为0.01,批大小为64,优化器为Adam。
3.1.4 主要结果及机电设备预测效果论证为验证本研究方法在全因素条件下的预测性能,选取Kaplan-Meier,PF-ARIMA,CNN+GRU,CNN-LSTM这4类基线模型和本研究提出的多模态融合模型,简称HME-FULFusion模型。在SW-RUL-DATAS1,SW-RUL-DATAS2,SW-RUL-DATAS3这3个公开数据集上进行对比试验。所有模型均在相同数据切分、预处理与训练配置下评估,指标采用MSE与RMSE。各模型在MSE和RMSE指标上的结果如表 2所示。试验结果表明,本研究提出的HME-FuLFusion模型在全部数据集上均取得最低误差,验证了其有效性与鲁棒性。
| 基线模型 | Kaplan-Meier | PF-ARIMA | CNN+GRU | CNN-LSTM | HME-RULFusion | |||||||||
| MSE值 | RMSE值 | MSE值 | RMSE值 | MSE值 | RMSE值 | MSE值 | RMSE值 | MSE值 | RMSE值 | |||||
| SW-RUL-DATAS1 | 0.986 | 0.743 | 0.487 | 0.632 | 0.125 | 0.416 | 0.201 | 0.403 | 0.107 | 0.212 | ||||
| SW-RUL-DATAS2 | 0.945 | 0.802 | 0.590 | 0.421 | 0.129 | 0.554 | 0.192 | 0.557 | 0.131 | 0.269 | ||||
| SW-RUL-DATAS3 | 0.891 | 0.830 | 0.398 | 0.486 | 0.237 | 0.451 | 0.225 | 0.497 | 0.160 | 0.304 | ||||
对比试验结果表明,HME-RULFusion模型在多个数据集上表现出了优越的性能。在3个不同的SW-RUL-DATAS数据集上,HME-RULFusion模型相较于其他几种基线模型在MSE值和RMSE值这2个指标上均显示出更低的误差值。
对于SW-RUL-DATAS1数据集,HME-RULFusion在均方误差上达到了0.107,而在RMSE指标上为0.212,这2个指标都明显优于其他模型。Kaplan-Meier模型的MSE值为0.986,RMSE值为0.743,而基于ARIMA的方法分别为0.487和0.632。使用CNN+GRU的组合和CNN-LSTM的组合虽然在性能上有所提升,但仍不及本研究提出的模型。
在SW-RUL-DATAS2数据集中,HME-RULFusion模型的MSE值为0.131,RMSE值为0.269,仍然维持了相对较低的误差水平。其他模型中,CNN-LSTM的表现较为接近,其MSE值和RMSE值分别为0.192和0.557。
在SW-RUL-DATAS3数据集上,HME-RULFusion模型的MSE值和RMSE值分别为0.160和0.304,相比之下,其他模型如Kaplan-Meier和ARIMA的误差值较高,显示了HME-RULFusion模型在处理复杂数据时的鲁棒性。
综上所述,在多种数据特性与工况条件下,HME-RULFusion在MSE和RMSE指标上持续展现出更低的误差水平,证明了基于多模态输入与序列建模的寿命预测框架在高速公路机电设备场景中的有效性与鲁棒性。
为了更全面地评估模型对实际机电设备寿命预测的实用性,本研究还在SW-RUL-DATAS1所涵盖的多种机电设备类型(监控摄像机、照明系统、收费系统等)进行了分机电设备层面的预测效果对比。在不同机电设备、不同工况条件下,本模型整体的平均准确率、召回率等指标都有所提升,相对CNN+LSTM或ARIMA提升幅度为5%~15%,更能满足运维团队对故障预测的精度和提前量要求。
(1) 监控摄像机。在高湿度、多雨环境中故障率较高。本模型通过结合温度、湿度、瞬态电压、电流及维护日志信息,能提前2~5 d对可能发生的故障给出风险预警,而其他模型在故障发生前仅能提供较短期或不稳定的预判。
(2) 照明系统。照明系统常在夜间集中工作,环境因素和电气负载对其老化有显著影响。本研究模型在长序列分析中识别出“高负载+高湿度+连续维护记录”这一故障多发模式,准确率和召回率较CNN-LSTM方法提升了5%~10%。
(3) 收费系统。日常负载较平稳,故障更多受电子部件和外部环境干扰。本研究模型通过长序列分析及时捕捉到了轻微电流波动所带来的潜在故障苗头,减少了约10%的突然停机事件。
本研究模型在实践中取得更好的预测效果,主要归因于以下几方面。
(1) 充分利用多模态特征。在高速公路机电设备的实际应用中,单一数据源通常无法全面反映机电设备的真实健康状况。本研究通过整合环境传感器数据(温湿度)、瞬态电气数据(电压、电流)及文本维护记录(日志、维修记录)等,系统地捕捉机电设备外部环境、内部状态及历史维护事件。因此,模型在更高层次上理解了环境、工况、维护这三者的交互关系,显著提升了对机电设备健康度和剩余寿命的刻画精度。
(2) 自编码融合方式的优势。相比于简单拼接或串联多模态数据,Autoencoder方式能更有效地完成降维与去冗余,将多模态特征映射到紧凑、统一的编码空间,减少噪声和重复信息。同时,自编码器的隐藏层实现了跨模态信息的互通协同,能够捕获诸如“高温环境伴随异常电流导致故障风险显著增加”等潜在关联,为后续预测提供了高质量的综合特征表示。
(3) 基于RNN的长序列时序建模。在寿命预测任务中,机电设备的健康状况具有长期的时间依赖特征。RNN在每个时间步会更新其隐藏状态,持续累积历史信息,从而更合理地推断当前状态与未来趋势。不仅如此,RNN还可在序列预测中融合不同模态的时变特征,如环境数据的周期性、瞬态电气特征的波动规律,以及维护记录的断续出现,从而更灵活地捕捉累积性老化或突发性故障。
(4) 端到端训练与整体优化。从特征抽取、自编码融合到RNN预测均置于同一个损失函数(如MSE)下进行统一训练,使得网络各层在同一目标指引下共同优化,从而让寿命预测更精确。与繁琐的手工特征工程相比,端到端方式减少了人为假设与偏差,也更易于在大量数据中自主发掘复杂模态间的高阶关联。如果需扩展到其他模态(例如振动、图像),只需在特征抽取与自编码端稍作调整,即可在相同架构下无缝对接训练。
(5) 鲁棒性与泛化能力。面对工业场景下常见的数据缺失、噪声扰动,乃至高频瞬态与低频环境数据同时并存,本模型能借助多模态融合和长序列RNN结构,对不同类型的数据进行有机整合并保持预测稳定。即使在多变的高速公路机电系统中,它也能通过对全局时间动态的持续关注、对多模态信息的充分运用,依然在真实繁杂的环境下维持较低的预测误差并展现较好的泛化能力。
简而言之,多模态特征抽取+自编码融合+RNN长序列时序建模的综合性架构,能在同一个端到端框架下高效整合多源数据,使模型对机电设备剩余寿命的预测更加全面、精细与稳定。这也是实测结果中,该端到端方法在多种评价指标上均显现出明显优势的根本原因。
3.2 数据敏感性试验为评估不同模块缺失对剩余寿命预测的影响,首先将Kaplan-Meier模型在SW-RUL-DATAS全量数据上的结果设为基线;将去掉变分约束模块的结果记为no-UC,将去掉残差精炼模型记为no-RR,将去掉时序混合模块的模型记为no-TH。将本研究方法在SW-RUL-DATAS全量数据上的完整结果记为HME-RULFusion,用于与基线及各消融设置进行对比。
在3个公开退化数据集(SW-RUL-DATAS1,SW-RUL-DATAS2,SW-RUL-DATAS3)上的数据敏感性试验结果如表 3所示。对比方法包括传统生存分析模型Kaplan-Meier、去除关键模块的3组消融模型(去掉变分约束no-VC,去掉残差精炼no-RR,去掉时序混合no-TH)及本研究提出的HME-RULFusion。评价指标采用MSE和RMSE,数值越小表示预测精度越高。试验结果表明,本研究模型在所有数据集上均取得最低的MSE和RMSE,验证了所提出框架对数据变化的稳健性与整体有效性。
| 基线模型 | Kaplan-Meier | no-VC | no-RR | no-TH | HME-RULFusion | |||||||||
| MSE值 | RMSE值 | MSE值 | RMSE值 | MSE值 | RMSE值 | MSE值 | RMSE值 | MSE值 | RMSE值 | |||||
| SW-RUL-DATAS1 | 0.986 | 0.743 | 0.859 | 0.709 | 0.236 | 0.523 | 0.125 | 0.226 | 0.107 | 0.212 | ||||
| SW-RUL-DATAS2 | 0.945 | 0.802 | 0.862 | 0.791 | 0.257 | 0.454 | 0.134 | 0.269 | 0.131 | 0.269 | ||||
| SW-RUL-DATAS3 | 0.891 | 0.830 | 0.890 | 0.772 | 0.272 | 0.501 | 0.168 | 0.330 | 0.160 | 0.304 | ||||
由表 3可知,HME-RULFusion在3个数据集上均取得最低或并列最低的误差水平,体现出在全因素条件下的稳定领先。与Kaplan-Meier及各消融配置相比,这些数值在3组数据上均表现出一致而显著的优势,这表明完整框架能够在不同工况与数据分布下保持误差控制的稳定性。
从消融对比看,去除不同模块对性能的影响存在清晰的梯度关系。在SW-RUL-DATAS1上,去除变分约束(no-VC)后,误差上升至0.859/0.709,已接近传统基线(Kaplan-Meier:0.986/0.743);去除残差精炼(no-RR)则导致中度退化(0.236/0.523);去除时序混合(no-TH)带来较小但可感知的劣化(0.125/0.226)。同样的相对排序在SW-RUL-DATAS2与SW-RUL-DATAS3中重复出现:no-VC的误差分别为0.862/0.791与0.890/0.772,no-RR为0.257/0.454与0.272/0.501,no-TH为(MSE值为0.134, RMSE值为0.269)与(MSE值为0.168, RMSE值为0.330),而完整配置则维持在(MSE值为0.131, RMSE值为0.269)与(MSE值为0.160, RMSE值为0.304)。由此可见,误差水平按“no-VC、no-RR、no-TH、HME-RULFusion的顺序逐级下降,模块贡献的相对重要性具有跨数据集的一致性。
通过对融合表示上引入先验正则,变分约束有效抑制噪声放大与过拟合,控制极值误差的第1道关口;残差精炼在多尺度与多模态汇聚之后对系统性偏差进行细化矫正,是收敛至低偏差解的重要机制;时序混合用于捕捉跨尺度依赖与长程动态,其收益在极端工况下更为明显。三者协同作用形成完整框架的性能优势,一旦移除任一关键环节,误差便按上述规律梯度上升。
这些对比同时给出面向工程应用的改进启示。(1)正则化层面的约束不可或缺,若采集环境噪声较大或样本量受限,可在变分约束之外引入信息瓶颈或对比学习项以增强稳健性。(2)结构层面的残差路径应保持足够的表达能力与训练可达性,可结合可学习门控或分层残差以进一步降低收敛方差。(3)时序层面的混合机制在资源受限部署中可采用轻量化变体,以在延迟与精度之间取得折中。值得注意的是,即便在关键模块被移除的情形下,3种消融配置在3套数据上仍普遍优于Kaplan-Meier,这说明该框架具备一定的信息冗余与跨模态补偿能力,具备对模块降级与算力约束的适应性。
综上所述,完整的多模态融合与多模块协同是获得最优寿命预测性能的关键条件;在不同数据集与工况下,HME-RULFusion在MSE和RMSE指标上持续保持最低误差,既体现出对全因素信息的有效利用,也展示了在模块缺失或性能退化条件下的鲁棒性与可部署性。
4 应用与前景 4.1 实际应用场景与效果评估本研究模型已在广州市某高速公路资产智能管控平台中投入使用。由于数据样本限制,暂未将设备品牌、型号纳入关键因素,但在持续观测相同品牌、型号的机电设备寿命过程中,已取得显著成效。本研究将模型部署于50台摄像机与20处照明系统,基于统一评测协议获得的结果显示:总体准确率约为85%~90%,召回率约为80%,F1分数约为0.85,相较CNN-LSTM或PF-ARIMA等基线模型提升5%~10%;在同等部署条件下,Kaplan-Meier与ARIMA对短期波动与突发事件的敏感性较弱,而本研究依托多模态输入与时序建模能够更早识别异常并给出预警窗口。
典型案例表明,在雨季湿度骤升时,系统可提前约3 d提示多台摄像机的高风险并指导维护,避免集中停机;在照明系统连续一个月出现电流微幅波动的情形下,模型结合温度与维护日志判定部件老化并定位到具体回路,诊断一致性与命中率优于传统时间序列方法。用户侧反馈显示,依据模型输出制订的预防性维护计划使故障率下降20%~30%,突发停机显著减少,配套可视化界面能够直观呈现寿命与风险趋势,为资产调度与备品备件计划提供数据支撑;经济性评估表明,单台设备年度维修成本降低10%~15%,紧急检修率下降,按试点口径推算年综合成本节省达数十万元,同时设备可用率与整体运营效率随之提升。
在可扩展性方面,模型可通过分布式训练与分模块并行在数十台至数千台规模下稳定运行;在适配性方面,对智能照明、可变情报板与隧道通风等资产仅需在前端特征提取与自编码器结构上进行有限调整即可引入新模态。进一步的跨域迁移(如城市交通信号、铁路信号与桥梁健康监测)虽具备可行性,但需针对目标系统的运行机理与数据形态对模态选择、采样频率与特征工程进行再设计,并在必要时增设传感器或采用新的表征方式,以确保其在不同工业与交通场景中的稳健泛化与可靠落地。
4.2 对维护决策的支持本研究的预测模型通过整合多模态数据和采用先进的机器学习技术,为设备维护决策提供了强大的数据支持。模型能够实时监测设备状态,并预测其可能的故障时间,有助于运维团队优化维护计划和资源配置,减少因设备故障导致的意外停机和维护成本。
4.3 未来发展方向随着数据规模和计算能力的提升,本研究模型可以结合前沿技术,实现更智能、更可解释、更实时的机电设备寿命预测。在未来工作中,可从多项技术路径协同推进以提升机电设备寿命预测的有效性与可部署性[15]。一方面,利用预训练语言模型(如GPT,BERT)对维护日志进行深层语义表征,并与电气、环境等模态实现无缝融合,以迁移学习机制构建能够在不同设备与场景间快速适配的大规模预测模型;另一方面,构建覆盖设备结构、运行状态、维修事件与环境要素的知识图谱,用体系化先验增强特征解释性,并结合图神经网络挖掘设备之间的潜在关联模式以提升跨设备泛化。为实现预测与运维联动,可引入强化学习对维护策略进行在线优化,动态调整数据采集与处理流程中的关键参数,使寿命预测与维护决策形成闭环。依托物联网与边缘计算的演进,可在现场实现实时采集与就地推理:在设备端部署传感器与边缘节点以完成滤波与标准化等预处理,通过剪枝、量化(如INT8,FP16)与知识蒸馏实现模型轻量化以满足算力约束,并在带宽或资源受限时采取更简化的模型或推理策略以保障时延,同时定期由云端统一更新关键数据与模型权重并下发至边缘侧,从而在实时性与准确性之间取得稳健平衡。
5 结论 5.1 主要研究发现本研究依托2017年10月至2023年9月在3条运营高速公路上累计8 200套机电设备的实际运行数据,历时4个月开发了一种基于多尺度的多模态数据融合的高速公路机电设备寿命预测模型。试验表明模型在多个测试数据集上具有优越的预测性能。数据敏感性试验表明,每种数据类型均对模型的预测结果具有显著影响,尤其是瞬态电压、电流的状态对机电设备寿命有非常大的影响,也验证了多模态数据融合在提升预测准确性方面的重要性。
5.2 对未来工作的建议(1) 拓展环境因素的考虑范围。本模型中仅包含温度和湿度作为环境因素,未来建议增加更多可能对机电设备寿命产生重要影响的环境参数。例如,在高海拔地区,应考虑低压、低氧等影响因素;隧道内机电设备则需关注油污、粉尘的沉积对机电设备性能的长期侵蚀;滨海地区的盐雾腐蚀对机电设备材料的加速老化更是一个关键因素。通过引入这些参数并在模型中进行多模态融合,可以更全面地反映机电设备所处环境对其寿命的实际影响,从而提升预测的准确性和适用性。
(2) 引入更先进的机器学习技术。未来可以结合大模型技术、知识图谱技术及强化学习技术,以进一步提升模型的预测能力和适应性。例如,通过知识图谱技术构建机电设备运行与维护之间的因果关联,强化学习可优化机电设备在动态环境中的运行策略,而大模型技术则能支持复杂多模态数据的深度学习。这些技术的融合应用将显著提升模型在复杂场景下的预测精度和决策能力。
(3) 研发适用实时监测的轻量级模型。为满足实时监测与预测的需求,应专门开发能够直接部署在边缘侧的轻量级模型。首先在架构层面,可以优先使用MobileNet和TinyTransformer或经过压缩的卷积网络,这类网络参数量和计算量均较小,能够在机电设备本地运行而不占用过多资源。其次,通过剪枝、量化等模型压缩手段去除冗余参数,同时利用知识蒸馏把复杂大模型的知识迁移到小模型,确保压缩后的精度仍然可靠。最后,将流数据处理模块嵌入模型内部,使其能够持续接收并解析来自物联网传感器的实时信号,动态调整预测窗口;如果现场配有GPU或TPU等硬件加速器,还可以进一步缩短推理延迟。采用这套方案后,模型可在各类工业现场即插即用,实现对机电设备状态的毫秒级更新与故障预判,从而显著提升设备管理的智能化水平,并为更多工业场景提供通用、高效的实时决策支持。
| [1] |
杨艺, 付道一, 雍彬. 基于ARIMA风电机组齿轮箱故障趋势预测方法研究[J]. 重庆工商大学学报(自然科学版), 2019, 36(3): 87-93. YANG Yi, FU Daoyi, YONG Bin. Research on fault trend prediction method of wind turbine gearbox based on ARIMA[J]. Journal of Chongqing Technology and Business University (Natural Sciences Edition), 2019, 36(3): 87-93. |
| [2] |
文昌俊, 陈洋洋, 何永豪, 等. 基于混合威布尔分布的水稻插秧机的可靠性分析及剩余寿命预测[J]. 科学技术与工程, 2024, 24(1): 163-169. WEN Changjun, CHEN Yangyang, HE Yonghao, et al. Reliability analysis and residual life prediction of rice transplanter based on hybrid Weibull distribution[J]. Science Technology and Engineering, 2024, 24(1): 163-169. |
| [3] |
张金泽, 单甘霖. SVM技术与ANN方法对旋转机械故障诊断性能的比较[J]. 电光与控制, 2006, 13(3): 72-74. ZHANG Jinze, SHAN Ganlin. Comparison of fault diagnosis performances based on SVM and ANN[J]. Electronics Optics & Control, 2006, 13(3): 72-74. |
| [4] |
谢楠, 马振国, 唐兵, 等. 继电保护设备剩余寿命预测的智能算法研究[J]. 兰州理工大学学报, 2023, 49(2): 83-87. XIE Nan, MA Zhenguo, TANG Bing, et al. Study on intelligent algorithm for remaining useful life prediction of relay protection equipment[J]. Journal of Lanzhou University of Technology, 2023, 49(2): 83-87. |
| [5] |
QU G X, QIU T, SI Y, et al. Remaining useful life prediction for aero-engine based on hybrid CNN-GRU model[C]// Proceedings of 2022 IEEE International Conference on Unmanned Systems (ICUS). New York: IEEE, 2022.
|
| [6] |
徐先峰, 赵龙龙, 夏振. 基于CNN- LSTM的轴承故障智能诊断方法研究[J]. 自动化仪表, 2020, 41(12): 27-33. XU Xianfeng, ZHAO Longlong, XIA Zhen. Research on intelligent fault diagnosis method for bearings based on CNN-LSTM[J]. Process Automation Instrumentation, 2020, 41(12): 27-33. |
| [7] |
刘惠, 刘振宇, 郏维强, 等. 深度学习在装备剩余使用寿命预测技术中的研究现状与挑战[J]. 计算机集成制造系统, 2021, 27(1): 34-52. LIU Hui, LIU Zhenyu, JIA Weiqiang, et al. Current research and challenges of deep learning for equipment remaining useful life prediction[J]. Computer Integrated Manufacturing Systems, 2021, 27(1): 34-52. |
| [8] |
韩林洁. 基于CNN和GRU的滚动轴承退化状态评估及剩余寿命预测[D]. 北京: 机械科学研究总院, 2020. HAN Linjie. Rolling bearing degradation state evaluation and residual life prediction based on CNN and GRU[D]. Beijing: China Academy of Machinery Science and Technology, 2020. |
| [9] |
周亚鹏, 郭彪, 王一纯. 基于PF-ARIMA的锂离子电池剩余寿命预测[J]. 电池工业, 2022, 26(1): 19-22. ZHOU Yapeng, GUO Biao, WANG Yichun. A remaining useful life prediction method for lithium-ion battery based on PF-ARIMA[J]. Chinese Battery Industry, 2022, 26(1): 19-22. |
| [10] |
陈保家, 陈学力, 沈保明, 等. CNN-LSTM深度神经网络在滚动轴承故障诊断中的应用[J]. 西安交通大学学报, 2021, 55(6): 28-36. CHEN Baojia, CHEN Xueli, SHEN Baoming, et al. An application of convolution neural network and long short-term memory in rolling bearing fault diagnosis[J]. Journal of Xi 'an Jiaotong University, 2021, 55(6): 28-36. |
| [11] |
蔡文斌, 李文, 胥元刚. 基于三参数威布尔分布模型的超高强度抽油杆概率疲劳寿命曲线[J]. 中国石油大学学报(自然科学版), 2022, 46(4): 79-85. CAI Wenbin, LI Wen, XU Yuangang. Probabilistic fatigue life curve of ultra-high strength sucker rods based on a three-parameter Weibull distribution model[J]. Journal of China University of Petroleum (Edition of Natural Science), 2022, 46(4): 79-85. |
| [12] |
王乔方, 郑万祥, 王冲文, 等. 基于威布尔分布的某半导体器件贮存寿命分布规律初探[J]. 红外技术, 2020, 42(11): 1077-1080. WANG Qiaofang, ZHENG Wanxiang, WANG Chongwen, et al. Preliminary study on storage life distribution of semiconductor device based on Weibull distribution[J]. Infrared Technology, 2020, 42(11): 1077-1080. |
| [13] |
缪吉昌, 纪晓宏, 王兆源, 等. 基于威布尔分布的婴儿培养箱关键部件的剩余寿命预测[J]. 中国医学物理学杂志, 2021, 38(9): 1162-1167. MIAO Jichang, JI Xiaohong, WANG Zhaoyuan, et al. Estimation of the remaining useful life of critical component of infant incubator based on Weibull distribution[J]. Chinese Journal of Medical Physics, 2021, 38(9): 1162-1167. |
| [14] |
黄中华, 代兵, 陈晋豪, 等. 风浪联合作用下海上风电机组塔筒疲劳寿命分析[J]. 机械设计, 2022, 39(增2): 145-149. HUANG Zhonghua, DAI Bing, CHEN Jinhao, et al. Fatigue life analysis of tower of offshore wind turbine under combined action of wind and wave[J]. Journal of Machine Design, 2022, 39(S2): 145-149. |
| [15] |
邹才能, 熊波, 薛华庆, 等. 新能源在碳中和中的地位与作用[J]. 石油勘探与开发, 2021, 48(2): 411-420. ZOU Caineng, XIONG Bo, XUE Huaqing, et al. The role of new energy in carbon neutral[J]. Petroleum Exploration and Development, 2021, 48(2): 411-420. |
| [16] |
李天奇, 张顶学, 王亚. 基于有限元模拟的应力腐蚀对带腐蚀坑抽油杆寿命的影响[J]. 热加工工艺, 2020, 49(8): 51-57. LI Tianqi, ZHANG Dingxue, WANG Ya. Effect of stress corrosion on life of sucker rod with corrosion pit based on finite element simulation[J]. Hot Working Technology, 2020, 49(8): 51-57. |
| [17] |
方龙, 李良碧, 李荣富. 海上漂浮式风力机支撑结构疲劳寿命研究[J]. 太阳能学报, 2016, 37(12): 3184-3188. FANG Long, LI Liangbi, LI Rongfu. Fatigue life research of support structure for floating offshore wind turbine[J]. Acta Energiae Solaris Sinica, 2016, 37(12): 3184-3188. |
| [18] |
王健, 孙志礼, 于震梁, 等. 基于支持向量机的机械零件剩余寿命区间估计[J]. 东北大学学报(自然科学版), 2016, 37(7): 974-978. WANG Jian, SUN Zhili, YU Zhenliang, et al. Remaining useful life interval estimation for machine parts based on SVM[J]. Journal of Northeastern University (Natural Science), 2016, 37(7): 974-978. |
| [19] |
于泉, 郭增增, 梁锐. 基于马尔科夫链的高速公路机电设备寿命预测研究模型[J]. 公路交通科技, 2018, 35(1): 28-35. YU Quan, GUO Zengzeng, LIANG Rui. A prediction model of expressway electromechanical equipment life based on Markov chain[J]. Journal of Highway and Transportation Research and Development, 2018, 35(1): 28-35. DOI:10.3969/j.issn.1002-0268.2018.01.005 |
| [20] |
姜万录, 赵岩, 李振宝, 等. 多模型Stacking集成学习的旋转机械故障诊断方法[J]. 液压与气动, 2023, 47(4): 46-58. JIANG Wanlu, ZHAO Yan, LI Zhenbao, et al. Fault diagnosis method for rotating machinery based on multi-model Stacking ensemble learning[J]. Chinese Hydraulics & Pneumatics, 2023, 47(4): 46-58. |
| [21] |
肖迁, 焦志鹏, 穆云飞, 等. 基于LightGBM的电动汽车行驶工况下电池剩余使用寿命预测[J]. 电工技术学报, 2021, 36(24): 5176-5185. XIAO Qian, JIAO Zhipeng, MU Yunfei, et al. LightGBM based remaining useful life prediction of electric vehicle lithium-ion battery under driving conditions[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5176-5185. |
| [22] |
陈轲, 黄民, 李一鸣. 基于CNN-LSTM和注意力机制的轴承故障诊断方法[J]. 北京信息科技大学学报(自然科学版), 2022, 37(6): 26-31. CHEN Ke, HUANG Min, LI Yiming. Bearing fault diagnosis method based on CNN-LSTM and attention mechanism[J]. Journal of Beijing Information Science & Technology University, 2022, 37(6): 26-31. |
| [23] |
邱佩臻, 吴东燃, 夏艺, 等. 循环神经网络在剩余使用寿命预测中的应用综述[J]. 现代信息科技, 2023, 7(24): 61-66. QIU Peizhen, WU Dongran, XIA Yi, et al. Review on the application of recurrent neural networks in the prediction of remaining service life[J]. Modern Information Technology, 2023, 7(24): 61-66. |
| [24] |
邹旺, 江伟, 冯俊杰, 等. 基于ANN和SVM的轴承剩余使用寿命预测[J]. 组合机床与自动化加工技术, 2021(1): 32-35. ZOU Wang, JANG Wei, FENG Junjie, et al. Bearing remaining useful life prediction based on artificial neural network and support vector machine[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2021(1): 32-35. |
 2025, Vol. 42
2025, Vol. 42



 ,
,