扩展功能
文章信息
- 钱勇生, 徐金元, 曾俊伟, 魏谞, 张富涛, 李信.
- QIAN Yongsheng, XU Jinyuan, ZENG Junwei, WEI Xu, ZHANG Futao, LI Xin
- 山区高速公路弯道路段异质交通流特性研究
- Heterogeneous traffic flow characteristics in expressway curve sections in mountainous regions
- 公路交通科技, 2025, 42(9): 1-11
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(9): 1-11
- 10.3969/j.issn.1002-0268.2025.09.001
-
文章历史
- 收稿日期: 2024-10-17
山区高速公路弯道交通流运行环境复杂,交通事故频发,驾驶员需在弯道处时刻调整车速和车辆位置以确保安全通过。随着自动驾驶技术的发展,人工驾驶与自动驾驶混行交通流等成为研究热点。元胞自动机模型是一种离散动态模型,在自动驾驶领域的仿真研究日益受重视。该模型能有效模拟交通流演化过程,可分析不同自动驾驶策略对交通流的影响,如车辆跟驰行为、换道决策等,通过参数调整和优化能更好理解混行交通流中车辆相互作用机制,还可为交通管理部门提供决策支持,以适应混行交通环境。
在模拟和预测弯道交通流的行为中,不同交通流模型(宏观模型、微观模型等)[1]都各自有其适用范围,利用元胞自动机进行建模仿真是一种有效的方法。元胞自动机[2]模拟了交通流中车辆之间的相互作用和驾驶员的决策过程,能够在微观水平上考虑每辆车的行驶轨迹和速度变化,后经NaSch模型[3]、IDM模型[4]演化发展至今,并引入Gipps安全距离模型[5]、GM刺激反应类模型[6]等跟驰模型,方法已趋于成熟。目前,关于弯道异质交通流的研究还较少,大多利用元胞自动机模型对普通车辆进行弯道交通流建模分析,梁玉娟[7]、庞明宝[8]在经典的NaSch模型基础上,从不同弯道曲线半径、道路摩擦系数等条件对弯道交通流进行分析,得到弯道曲线半径、道路摩擦系数是影响弯道交通流主要因素的结论,但未对弯道结构进行细分,仅将弯道路段看作固定曲率的曲线;此外,龚莉[9]结合雾天交通特性,分析弯道曲率对高速公路造成的各种影响,结果表明车辆在弯道路段的安全速度随着弯道曲率的增大而减小。许得杰[10]对不同弯道条件的交通流特性进行分析,发现弯道曲线半径和道路摩擦系数对交通流的影响都存在一个临界值。秦严严[11]综合考虑速度差、弯道半径和汽车最小转弯半径等因素,建立网联车辆弯道跟驰模型,分析各关键参数对弯道交通流稳定性的影响。同时弯道线形方面,有学者对单一车辆在弯道处行驶受线形变化的影响机理进行分析,陈志贵[12]对山区高速公路直线与平曲线组合路段对驾驶员加减速行为进行研究,分析得出平曲线曲率对驾驶员驾驶行为具有明显影响;Zhu[13]从摩擦系数和曲率半径两方面探究其对弯道交通流的影响,提出了一种新的车辆曲线运动模型,为本文研究弯道曲率变化提供参考;车辆横向扰动也是建模仿真中重要的考虑因素,邓天民[14]、陈莹[15]、戢晓峰[16]在山区复杂线形公路上开展实车驾驶试验,分析行驶轨迹偏移特性,对弯道处驾驶风险进行判别,讨论弯道对车辆横向干扰的影响因素,验证了本文研究方向的正确性;Pal[17]从横向和纵向交互作用的影响出发,建立不同车辆类型的异质交通流元胞自动机模型,考虑了车辆轨迹变化对交通流的影响,但未从弯道线形构成角度进行分析。
上述学者丰富了弯道交通流的建模和仿真研究,说明了弯道作为一种特殊的交通瓶颈,会诱发复杂的交通现象,特别是在不同的弯道曲线半径、不同的天气、不同弯道线形组成的情况下,车辆横纵向稳定性变化频繁,严重影响车辆速度和道路整体通行效率。基于此, 本研究建立考虑弯道路段的双车道元胞自动机模型, 模拟山区弯道路段交通特性,分析不同弯道条件对交通流的影响,明确缓和曲线最优比例和智能网联车辆的积极作用。
1 弯道路段交通特征分析山区高速公路平面线受地形、地物的限制必须转折,为了保证线形的平顺连续,通常会设置圆曲线段用以过渡,但圆曲线不可避免会出现转折点,影响道路平顺性,故在直线和圆曲线之间增设缓和曲线用以过渡,使线路能够满足驾驶的安全性和舒适性。直线、缓和曲线、圆曲线是平面线形构建的三要素。在公路的平面设计中,根据实际需求,采用圆曲线、回旋线及其各种复杂组合形式进行衔接。
山区高速公路弯道平面线形组合较多,本研究以最常见的“基本型”平曲线:直线-回旋线-圆曲线-回旋线-直线,作为山区高速公路弯道路段的研究对象,通过分析“基本型”平曲线的线形组合和车辆过弯的驾驶行为,考虑影响车辆行驶的参数。对于长度的设置,公路弯道在一般情况下是由2段缓和曲线(或超高、加宽缓和段)和1段圆曲线组成,缓和曲线的长度不能小于该级公路对其最小长度的规定,中间圆曲线的长度宜有大于3 s的行程。当条件受限时,可将缓和曲线在曲率相等处对接,此时的圆曲线长度为0。平曲线一般最小长度为9 s行程,极限最小长度为6 s行程[18],故本研究暂设弯道长度为300 m。
1.1 缓和曲线缓和曲线的设置是为了使直线到圆曲线的过渡更为顺畅,使车辆在行驶过程的曲率变化逐渐过渡,协调曲率变化和速度平顺。为尽量提高车辆过弯的舒适性和安全性,减少行车震荡的情况,通常利用回旋线作为过渡曲线,当改变缓和曲线长度时,车辆过弯轨迹不同,弯道内车辆曲率半径也不相同。
| $ R \cdot L_{\mathrm{s}}=A^2, $ | (1) |
| $ R^{\prime}=\frac{A^2}{L_{\mathrm{s}}^{\prime},} $ | (2) |
式中,R为圆曲线曲率半径;R′为缓和曲线曲率半径;Ls为缓和曲线全长;Ls′为行驶轨迹长度;A2为回旋线参数。
在《公路工程技术标准》(JTG B01—2014)中规定:除了四级公路直线与小于不设超高最小半径的圆曲线相衔接处可不设缓和曲线,其余各级公路都应设置缓和曲线。因此,为了避免驾驶员操作过于匆忙,提高乘客舒适性,缓和曲线必须满足一定的长度,规范中以在缓和曲线上行驶时间不小于3 s作为要求,规定了不同等级高速公路缓和曲线的最小长度, 见表 1。
| 设计速度/(km·h―1) | 高速公路 | 一级公路 | 二级公路 | 三级公路 | 四级公路 | ||||||||||
| 120 | 100 | 80 | 100 | 80 | 60 | 80 | 60 | 40 | 30 | 20 | |||||
| 缓和曲线最小长度/m | 100 | 85 | 70 | 85 | 70 | 50 | 70 | 50 | 35 | 25 | 20 | ||||
1.2 道路摩擦系数
道路摩擦系数是衡量道路表面与车辆轮胎之间摩擦力大小的重要指标,对车辆的行驶安全、操控性能以及道路的通行效率起着至关重要的作用,在转弯、加速等过程中,良好的摩擦系数能够提供足够的侧向力和牵引力,使车辆保持稳定的行驶状态,但道路摩擦系数不是固定不变的,受天气影响,如雨天、雪天、雾天及高温等,路面会湿滑或变软,从而降低摩擦系数,影响道路安全。由《公路工程技术标准》(JTG B01—2014)可知,一般沥青路面的摩擦系数为0.4~0.8,混凝土路面的摩擦系数值为0.4~0.6。
1.3 车辆过弯速度车辆行驶在弯道路段会受到横向离心力影响。车辆操控方面,当车辆行驶在弯道路段,产生的离心力需要轮胎与路面的摩擦力来抵消,由于弯道半径和离心力之间存在的关系,利用弯道半径也可以确定临界安全速度。临界速度是指车辆在通过弯道时为保证车辆不发生侧翻或滑移所能达到的最大容许速度。
| $ V \geqslant \sqrt{\frac{R}{127(\mu+h)}}, $ | (3) |
式中,R为弯道最小半径;V为最大容许速度;μ为横向力系数;h为横向超高横坡。
2 建立仿真模型 2.1 运行规则本研究建立由人工驾驶车辆和智能驾驶车辆混行的异质交通流模型,根据人工驾驶车和智能驾驶车在过弯时轨迹曲线选择的差异,以及反应时间、跟驰距离、安全间距、加速度、减速度等参数的不同,利用Gipps安全距离模型构造出人工驾驶车与智能驾驶车不同的演化规则,并考虑二者在弯道路段驾驶行为的不同,提出不同类型车辆的过弯行驶轨迹,以更加真实地反映人-智混行的异质交通流特性。
2.1.1 安全距离经典的Gipps安全距离模型综合考虑了多种因素对安全距离的影响,包括车辆加速度、安全距离限制、车辆物理尺寸、加减速性能和驾驶员反应时间等。安全距离dn, safe是指前车采取紧急刹车驾驶行为时,跟驰车辆为避免碰撞所采取的安全车间距,与跟驰车辆自身性能、前车制动能力以及跟驰车辆的反应时间有关。Gipps不仅可以反映出智能驾驶车的不同,还比较符合轨迹偏移需要的一些场景,可以灵活调整不同车辆类型的加速度、减速度和紧急减速度,例如反映横向间距对车辆的影响,较为符合本研究建模需要,公式[19]如下:
车辆为避免碰撞所采取的安全距离:
| $ \begin{gathered} d_{n, \text { safe }}(t)=x_{n-1}(t)-x_n(t)-l_{n-1}= \\ v_n(t) \tau_n+\frac{v_n(t)^2}{2 b_n}-\frac{v_{n-1}(t)^2}{2 b_{n-1}}, \end{gathered} $ | (4) |
车辆为避免碰撞所采取的安全速度:
| $ \begin{gathered} v_{\text {safe, } n}(t)=-b_n \tau_n+ \\ \sqrt{b_n^2 \tau_n^2+b_n\left(2 d_n-\tau_n v_n(t)+\frac{v_{n-1}^2(t)}{b_{n-1}}\right)}, \end{gathered} $ | (5) |
式中,dn, safe (t)为t时刻第n辆车的安全距离;xn (t)为t时刻第n辆车的位置;xn-1 (t)为t时刻第n辆车前方车辆的位置;ln-1为第n辆车前方车辆的车身长度;vn (t)为t时刻第n辆车的速度;vn-1 (t)为t时刻第n车辆前方车辆的速度;τn为第n辆车的反应时间;bn为第n辆车的最大减速度;bn-1为第n辆车前方车辆的最大减速度;vsafe, n (t)为t时刻第n辆车的安全速度;dn为第n辆车与前方车辆的车间距。
2.1.2 正常路段演化规则正常路段演化规则一般包括加速规则、匀速规则、减速规则、随机慢化规则,具体如下。
加速规则:当同一车道车辆与前车距离大于安全距离时,为了追求更高的期望速度,按如下规则加速:
| $ v_n(t+1)=\min \left(v_n(t)+a_n, v_{\max }, d_n, v_{\text {safe }, n}(t)\right) \text { 。} $ | (6) |
匀速规则:当车辆与前车距离等于安全距离时,当前车辆继续以相同的速度行驶,以保证行车安全,规则如下:
| $ v_n(t+1)=\min \left(v_n(t), d_n, v_{\text {safe }, n}(t)\right) 。$ | (7) |
减速规则:当车辆与前车距离小于安全距离时,为了保证车辆行驶安全驾驶员会进行减速操作,减速分为:前车车辆处于停车状态和前车处于运动状态2种情况。
当前方车辆处于停车状态时,采用安全性减速规则:
| $ v_n(t+1)=\max \left\{\min \left(v_{\text {safe }, n}(t), d_n-1\right), 0\right\}。$ | (8) |
当前方车辆处于行驶状态时,采用确定性减速规则:
| $ v_n(t+1)=\max \left\{\min \left(v_{\text {safe }, n}(t), d_n\right), 0\right\} \text { 。} $ | (9) |
随机慢化规则:为了反映驾驶员心理变化、路况、环境等各种随机因素导致的车辆随机减速行为,采用随机慢化概率pslow进行表征。由于智能车辆具有相对稳定和灵敏的控制性能,故对智能车辆不设置随机慢化,即随机慢化概率pslow=0。非智能车辆的随机慢化:
| $ v_n(t+1)=\max \left(v_n(t)-b_n, 0\right) \text {, if } \operatorname{rand}()<p_{\text {slow }} 。$ | (10) |
在速度演化后,车辆的空间位置也随之前进:
| $ x_n(t+1)=x_n(t)+v_n(t+1) \text { 。} $ | (11) |
换道动机:
| $ v_n(t+1)>d_n(t) \& \& v_n(t+1)<d_{n, \text { other }}(t) \text { 。} $ | (12) |
换道安全条件:
| $ v_{\text {safe, other }, n-1}(t)=v_{\max , \text { other }, n-1} \quad v_{\text {safe, other }, n}(t)=v_{\max , n}, $ | (13) |
| $ v_{\text {safe}, \text {other}, n-1}(t)<d_{n, \text {other,back}}(t) \& \& v_{\text {safe}, n}(t)<d_{n, \text {other }}(t), $ | (14) |
式中,vn (t+1)为t+1时刻车辆n的速度;dn (t)为t时刻车辆n与同一车道前车的距离;dn,other (t)为t时刻车辆n与侧车道前方车辆的距离;dn,other,back (t)为t时刻车辆n与侧车道后方车辆的间距;vsafe,other,n-1 (t)为当前车辆换道成功后与后车的安全速度;vsafe,n (t)为当前车辆的安全速度。
2.1.3 弯道路段演化规则在弯道中行驶,综合考虑弯道线形、摩擦系数、不同驾驶行为特点对车辆速度等影响,弯道路段安全距离和车辆安全速度等都与直道有着明显不同,具体演化规则如下所述。
安全速度:弯道路段安全速度与直道不同,本研究将弯道路段分为缓和曲线-圆曲线-缓和曲线三部分,缓和曲线段区别于其他文献中单一安全速度的方式,当车速过高时可能会出现车辆速度骤减等剧烈变化,这无法完全反映实际情况,现实中弯道路段很长,弯道的最高速度不是固定值,会随着线形的变化而改变。因此根据入弯的程度灵活调整安全速度的大小,使车辆在进出弯道时更为顺畅,通过改变Ls大小反映不同类型车辆的过弯轨迹:
| $ v_{\text {safe}, n}(t)=\sqrt{\frac{R^{\prime}}{127(\mu+h)}}, \quad \text { if } x_n \subset X_{\mathrm{b}}, $ | (15) |
| $ R^{\prime}=\frac{A^2}{L_{\mathrm{s}}^{\prime}}, \quad \text { if } x_n \subset X_{\mathrm{b}}, $ | (16) |
| $ L_{\mathrm{s}}^{\prime}=x_n-x_{\text {start }} \text { or } x_{\text {final }}-x_n, \text { if } x_n \subset X_{\mathrm{r}}, $ | (17) |
| $ L_{\mathrm{s}}^{\prime}=L_{\mathrm{s}}, \quad \text { if } x_n \subset X_{\mathrm{c}}, $ | (18) |
式中,Xb为弯道路段; Xr为缓和曲线路段,分为入弯缓和曲线段和出弯缓和曲线段; Xc为圆曲线路段。
为了更直观地比较拥堵情况,将以低于10 km/h速度在车道上行驶的车辆定义为拥堵车辆,通过计算拥堵车辆在整个车道系统中所占比例的大小来量化道路拥堵程度。交通流拥堵的计算规则记为:
| $ R_{\mathrm{C}}=\frac{n^{\prime}}{\Delta T \times N}, $ | (19) |
| $ k=\frac{N(t)}{L}, v(t)=\frac{1}{N} \sum\limits_{i=1}^N v_i(t), $ | (20) |
式中,RC为拥堵率;n′为拥堵车辆次数;ΔT为仿真时间;N为道路总车辆数;k为车辆密度;L为道路全长;v为t时刻平均速度。
2.2 参数确定本研究主要参考西南交通大学蒋阳升教授[21]和邱小平教授[19]建模的参数设置方法。采用周期性边界进行模拟,模拟道路总长度750 m,每辆车的初速度从0到vmax中随机选取,车辆最大速度33.3 m/s(120 km/h),车辆长度5 m。以单位时间内通过特定元胞位置的车辆数表征流量,元胞长度为0.5 m,道路长度1 500个元胞,仿真时长104s,取交通流稳定后的1 000 s的数据作为结果进行分析,其余参数设置见表 2。
| 参数 | 意义 | 取值 |
| ln | 车辆长度/m | 5 |
| τ1 | 人工车辆反应时间/s | 2 |
| τ2 | 智能车辆反应时间/s | 0.1 |
| an | 常规加速度/(m·s―2) | 3 |
| bn | 常规减速度/(m·s―2) | 2.5 |
| bn′ | 紧急减速度/(m·s―2) | 3.5 |
| pslow | 随机慢化概率 | 0.3 |
| Vmax,1 | 人工车辆期望速度/(km·h―1) | 110 |
| Vmax,2 | 智能车车辆期望速度/(km·h―1) | 120 |
3 仿真试验分析 3.1 验证模型准确性
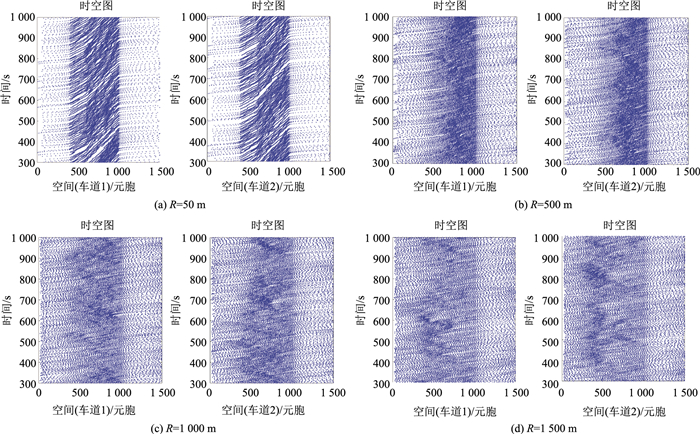
利用弯道曲线半径及摩擦系数分析对交通流影响,验证本模型的准确性。设定弯道长度300 m,摩擦系数0.15,车流密度0.2,在缓和曲线、圆曲线、缓和曲线比例为1∶1∶1条件下,对不同圆曲线半径进行数值模拟,如图 1时空图所示,其中400~1 000格子为弯道路段,横轴表示空间位置,纵轴表示时间,蓝色点为车辆位置。图中明显的深色区域为弯道路段对车辆造成的阻塞区域,即局部阻塞现象,在弯道路段外车辆处于自由流状态畅通行驶。随着半径的不断增加,时空图的阻塞现象逐步消散,当弯道半径增加至1 500 m时弯道对车辆造成的阻塞情况近乎消散,说明弯道半径的增加可以有效消除弯道对交通流的影响,弯道半径越大,交通流运行越顺畅,这与许得杰[10]描述一致。
|
| 图 1 不同半径时空图 Fig. 1 Spatiotemporal traffic diagrams with different radii |
| |
不同半径基本图如图 2所示,随着弯道半径的增大,速度-密度图(简称速密图)峰值流量也在不断增加,弯道半径越大,流量-密度图(简称流密图)的趋势越接近经典的NaSch基本图,当弯道半径增加至1 100 m后,流密图与NaSch基本图基本一致,且继续增加弯道半径峰值流量不再变化,说明弯道半径是影响弯道交通流的重要参数,当弯道半径达到一定值后弯道对交通流影响消失,情况与图 3相符。

|
| 图 2 不同半径基本图 Fig. 2 Fundamental diagrams with different radii |
| |

|
| 图 3 不同半径三维图 Fig. 3 Three-dimensional diagrams with different radii |
| |
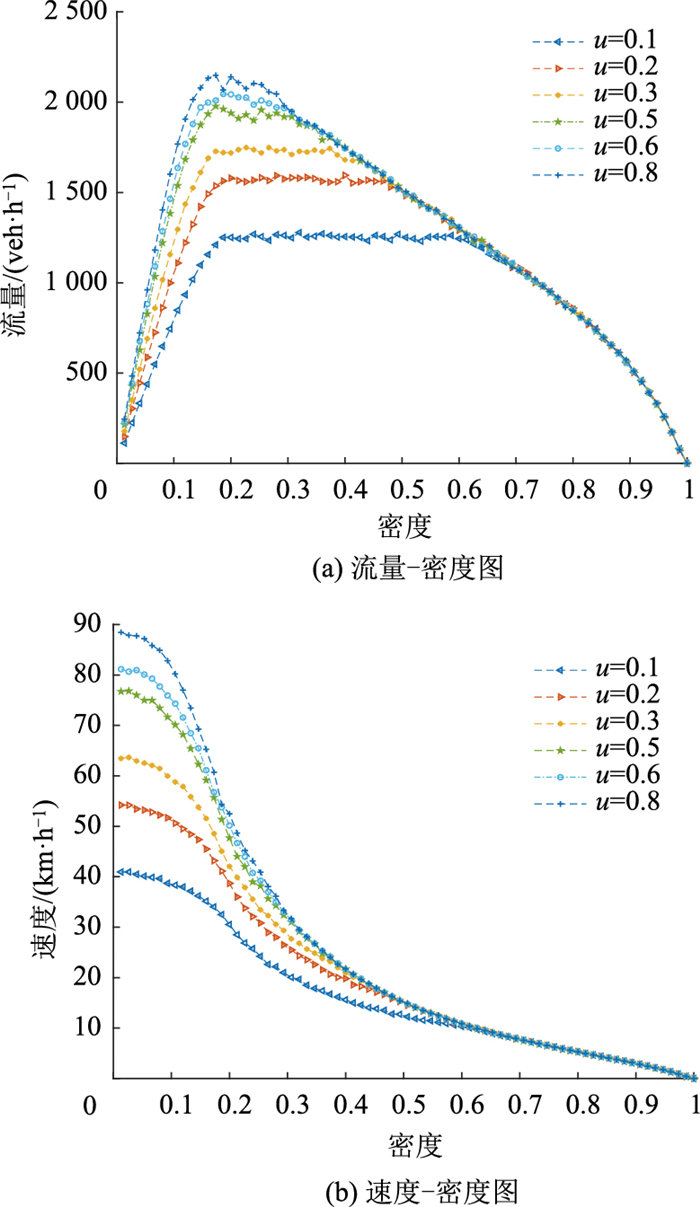
摩擦力是车辆驱动、减速和转向的动力来源,它决定着道路的通行能力和行驶安全,摩擦力受环境和道路路面的影响,因此探究不同摩擦系数对交通流的影响,改变摩擦系数对交通流基本图进行仿真如图 4所示。受弯道的影响,改变不同的摩擦系数同样会出现流量不随密度变化的平台期,随着摩擦系数的增大,平台期会向高流量位置偏移,且平台期出现的密度范围越小,所以摩擦系数的增大会提高道路通行能力;同时,从图 2(b)中也可以看出随着摩擦系数的增大,不同密度下的道路平均速度也越大,可以说明摩擦系数也是影响道路通行能力的关键因素,结果与梁玉娟[7]描述相似。
|
| 图 4 不同摩擦系数 Fig. 4 Fundamental diagrams with different friction coefficients |
| |
3.2 缓和曲线对交通流影响
多数模型在建模仿真时都将入弯缓冲段完全放在弯道区域之前,且弯道安全速度限定为一固定值,当弯道前车速过高时会出现车速急剧减小以达到弯道安全速度的情况,这与实际情况不符,实际高速公路弯道长度较长,车辆通常都是入弯后随着车辆离心力的增加而逐渐调整车速,且弯道安全速度也随弯道线形变化,并非是固定值。因此引入缓和曲线概念,利用回旋线的理论:随着车辆在弯道路段轨迹长度的变化,其安全速度也随之变化,将安全速度调整为不断变化的动态值,弥补了弯道路段限速单一的缺陷,更加符合实际情况。
为分析不同缓和曲线长度在弯道路段的占比对交通流的影响,以基本型平曲线来描述弯道路段的线形情况,入弯缓和曲线长度和出弯缓和曲线长度相等,缓和曲线比例
|
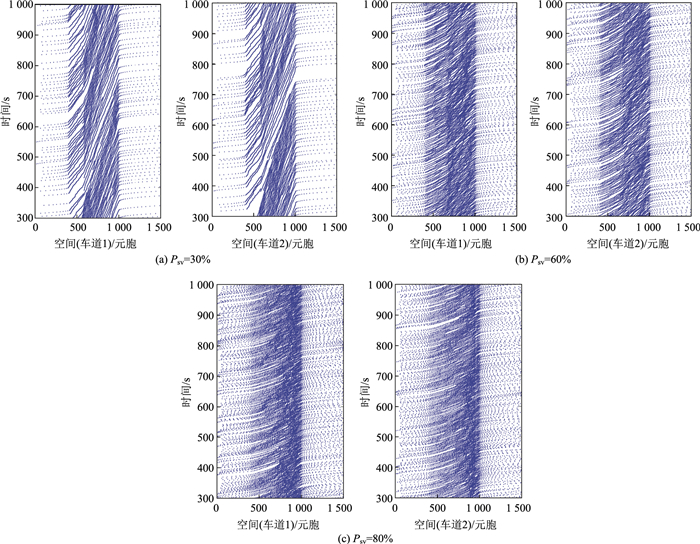
| 图 5 不同缓和曲线比例时空图 Fig. 5 Spatiotemporal traffic diagrams with different proportions of transition curves |
| |
|
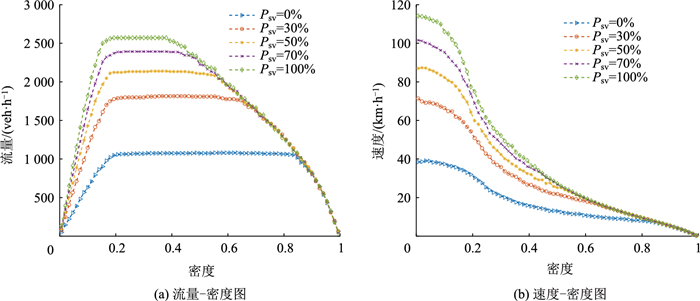
| 图 6 不同缓和曲线比例基本图 Fig. 6 Fundamental diagrams with different proportions of transition curves |
| |
|
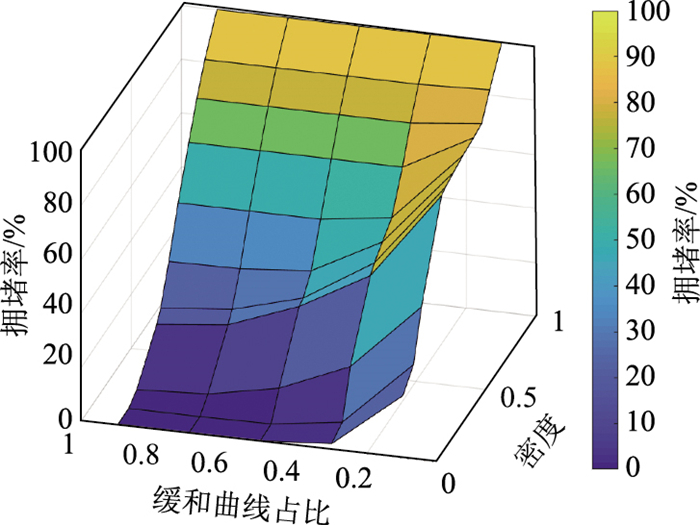
| 图 7 拥堵率三维图 Fig. 7 Three-dimensional diagrams with different congestion rates |
| |
如图 6所示,随着缓和曲线比例的上升,流量也会提高,但随着缓和曲线比例的增加,这种对交通流的改善效果也在降低,当缓和曲线参与比例在70%时(即入弯缓和曲线、圆曲线、出弯缓和曲线三者比例为35%∶30%∶35%)对交通流的改善效果最佳,继续提高缓和曲线比例对交通流的改善效果已不再明显,这与《公路路线设计规范》(JTG D20—2017)中对高速公路平曲线设计要求:设计速度大于或等于60 km/h时,回旋线—圆曲线—回旋线的长度以大致接近为宜内容一致。因此,可以说明弯道路段缓和曲线比例是影响交通流的重要因素,缓和曲线比例的提高会促进交通流的改善,当缓和曲线比例为70%时改善效果最佳。
同时,图 6(a)中会出现一段流量不随密度变化的平台期,流量平台期的出现符合实际交通情况,由于弯道“固定瓶颈”对车辆抑制作用的存在,弯道圆曲线半径越小,车辆受环境影响越严重,弯道对交通流的抑制作用越强,所以车辆在弯道附近越容易出现拥挤阻塞,车辆在弯道路段走走停停,在较长时间内无法从阻塞流转变为自由流,当车辆密度适中时,受弯道路段影响车辆间相互作用很大,但车辆又可以保持稳定行驶,由于弯道的存在,当车辆密度缓慢增加时这种稳定行驶的交通流状态也很难被破坏,从而导致平台期的出现。
3.3 智能车辆对交通流影响当车辆在弯道路段上行驶时,由于驾驶员的年龄、驾龄、性格等因素以及车辆性能的异同,对道路行驶曲线的选择,车速会有较大变化,各车型之间速度差明显,车辆之间相互影响严重。人工驾驶车辆在过弯过程中,主要依靠自身的驾驶经验和视觉判断来选择过弯轨迹,行驶在弯道路段会受到横向离心力影响,不适感和操作难度不断增加,通常会选择减少频调整车辆角度的操作,保持恒定角度过弯,因此在曲线比例的选择会倾向选择大比例圆曲线长期保持固定角度,以减少在缓和曲线段频繁调整角度的行为,故本研究将人工驾驶车辆的曲线比例设置为1∶2∶1。智能车辆会选择能够最小化车辆加速度和最佳比例的缓和曲线,以提高乘坐的舒适性,即缓和曲线、圆曲线、缓和曲线参与比例最接近1∶1∶1,故分析弯道路段智能车辆对交通流的影响,对不同渗透率的智能车辆进行仿真。
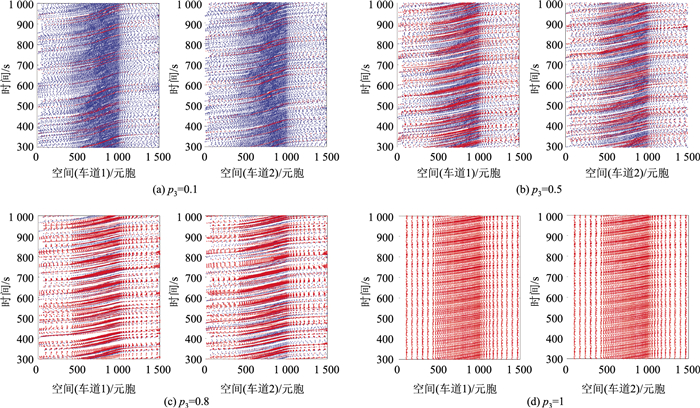
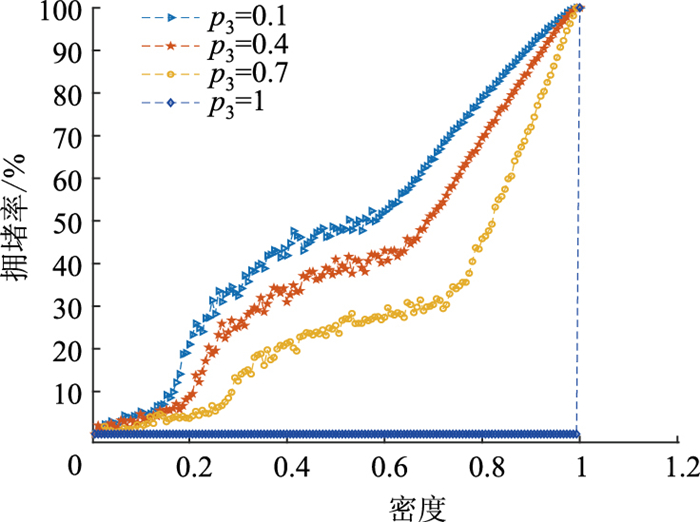
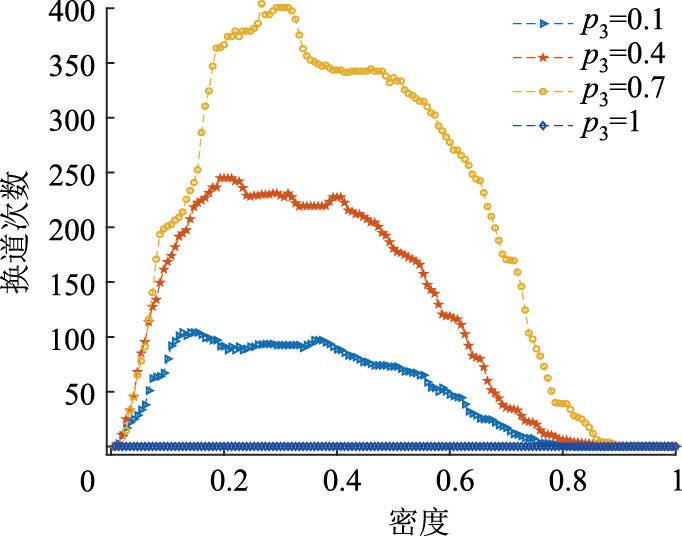
图 8是不同智能车渗透率时空图的情况,随着智能车辆渗透率提高,车辆过弯越顺畅,弯道的瓶颈效应表现越弱。智能车辆渗透率较低时,弯道路段中车辆速度都受到很显著的限制,其原因为普通车辆限制了交通流的提升,智能车辆受普通车的影响只能缓慢地跟驰在普通车后,随着智能车辆渗透率的增加,这种弯道路段速度被限制的情况并没有被改善,因为慢车仍然存在,还在继续影响智能车。当道路上全为智能车辆时,如图 10~11所示,情况发生质变,拥堵情况完全消失,拥堵率为0,轨迹图出现了很强的规律性,所有车辆在同一位置处都保持着相同的速度行驶,所有速度、加速度和减速度行为都保持高度一致,时空图轨迹图所有轨迹相同,同时车辆运行情况为理想状态,车辆不再换道,换道次数为0。
|
| 图 8 不同智能车渗透率时空图 Fig. 8 Spatiotemporal diagrams with different CAVs ' penetration rates |
| |
|
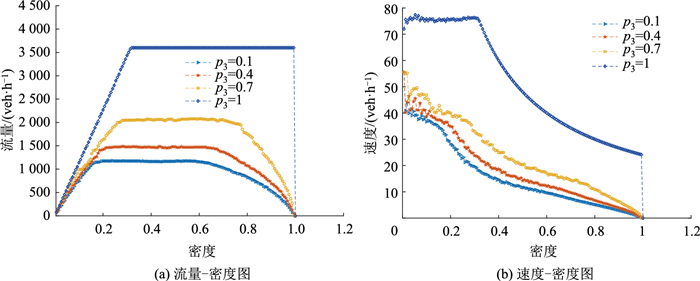
| 图 9 不同智能车渗透率基本图 Fig. 9 Fundamental diagrams with different CAVs ' penetration rates |
| |
|
| 图 10 不同智能车渗透率拥堵图 Fig. 10 Congestion diagrams with different CAVs' penetration rates |
| |
|
| 图 11 不同智能车渗透率换道次数 Fig. 11 Number of lane-changing with different CAVs' penetration rates |
| |
图 9为不同智能车渗透率基本图的情况,与其他条件下流密图相似,图 9(a)中也出现了流量平台期的现象,原因也是车辆间相互作用力小于弯道对车流的抑制作用。当交通流状态处于亚稳态流量平台期向阻塞流转变的过程中时,随着密度的增加,车辆间相互作用增大,对交通流的影响也逐渐大于弯道对交通流的影响,车流处于稳定行驶的亚稳态流量平台期逐渐被破坏,但随着智能车渗透率的增加,会改善车辆间的相互作用,因此需要更高的密度才能打破这种车流稳定行驶的亚稳态流量平台期。当智能车渗透率为1时,高密度时道路上全为智能车,车辆间相互作用恒定,且小于弯道对车流造成的影响,因此亚稳态流量平台期长期存在,不随流量增大而破坏。这与图 6(b)也可以相互印证,也说明智能车的参与可以有效改善交通流状态,提高道路通行能力。
4 结论本研究以元胞自动机模型作为基础理论模型,结合Gipps模型反映不同驾驶员反应时间、智能车辆加减速性能,分析研究车辆在弯道上运行轨迹特征、弯道线形影响、车辆类型特点,利用MATLAB编程进行数值模拟,得出以下主要结论:弯道缓和曲线比例对交通流具有显著影响,交通流在弯道位置会出现显著的“瓶颈”效应,改变缓和曲线比例可有效减小交通流的“瓶颈”效应,特别是当缓和曲线、圆曲线、缓和曲线参与比例为1∶1∶1时,交通流的改善效果最佳。同时,智能车辆的参与也会对弯道交通流产生显著影响。随着智能车辆渗透率的提高,交通流量显著提高,当道路上全为智能车后,交通环境发生质变,道路不再拥堵,且不会出现换道需求。并且,本研究体现了弯道交通流中独特的流量平台期现象,由于弯道路段对交通流的瓶颈抑制作用,自由流后会出现一段亚稳态流量平台期,在基本图中表现为流量恒定不随道路密度变化而改变。
| [1] |
秦严严. 交通流分析理论[M]. 北京: 人民交通出版社, 2023. QIN Yanyan. Theory of traffic flow analysis[M]. Beijing: China Communications Press, 2023. |
| [2] |
WACKER S. Cellular automata on group sets and the uniform Curtis-Hedlund-Lyndon theorem[J].
Natural Computing, 2019, 18(3): 459-487.
DOI:10.1007/s11047-017-9645-y |
| [3] |
PAN W, XUE Y, HE H D, et al. Impacts of traffic congestion on fuel rate, dissipation and particle emission in a single lane based on Nasch model[J].
Physica A: Statistical Mechanics and Its Applications, 2018, 503: 154-162.
DOI:10.1016/j.physa.2018.02.199 |
| [4] |
王树凤, 王世皓, 王新凯. 基于改进跟驰模型的混合车辆编队研究[J]. 公路, 2023, 68(6): 289-297. WANG Shufeng, WANG Shihao, WANG Xinkai. Research on hybrid vehicle formation based on improved car-following[J]. Highway, 2023, 68(6): 289-297. |
| [5] |
HE Y L, MONTANINO M, MATTAS K, et al. Physics-augmented models to simulate commercial adaptive cruise control (ACC) systems[J/OL]. Transportation Research Part C: Emerging Technologies, 2022, 139: 103692. (2022-04-27)[2024-10-16]. https://doi.org/10.1016/j.trc.2022.103692.
|
| [6] |
廖鹏, 杨文章, 褚明生, 等. 基于GM跟驰模型的内河限制性航道船舶交通流基本图[J]. 东南大学学报(自然科学版), 2022, 52(3): 602-608. LIAO Peng, YANG Wenzhang, CHU Mingsheng, et al. Fundamental diagram of vessel traffic flow in inland restricted waterway based on GM following model[J]. Journal of Southeast University (Natural Science Edition), 2022, 52(3): 602-608. |
| [7] |
梁玉娟, 薛郁. 道路弯道对交通流影响的研究[J]. 物理学报, 2010, 59(8): 5325-5331. LIANG Yujuan, XUE Yu. Study on traffic flow affected by the road turning[J]. Acta Physica Sinica, 2010, 59(8): 5325-5331. |
| [8] |
庞明宝, 任泊宁. 高速公路弯道雨天可能交通事故的CA模型仿真[J]. 中国安全科学学报, 2017, 27(7): 24-29. PANG Mingbao, REN Boning. Simulation of possible traffic accident in rainy weather on freeway curve using CA model[J]. China Safety Science Journal, 2017, 27(7): 24-29. |
| [9] |
龚莉. 驾驶行为与道路线形对高速公路雾天行车安全的影响机理研究[D]. 武汉: 中南财经政法大学, 2021. GONG Li. Influence mechanisms of driving behavior and road alignment on driving safety on freeway in fog weather[D]. Wuhan: Zhongnan University of Economics and Law, 2021. |
| [10] |
许得杰. 考虑不同弯道条件的交通流建模及模拟研究[D]. 兰州: 兰州交通大学, 2012. XU Dejie. Modeling and simulation of traffic flows considering different bend conditions[D]. Lanzhou: Lanzhou Jiatong University, 2012. |
| [11] |
秦严严, 廖小丽. 考虑速度差特性的网联车辆弯道跟驰模型[J]. 重庆理工大学学报(自然科学), 2024, 38(5): 10-17. QIN Yanyan, LIAO Xiaoli. Curve car-following model of connected vehicle considering velocity difference characteristics[J]. Journal of Chongqing University of Technology (Natural Science), 2024, 38(5): 10-17. |
| [12] |
陈志贵, 王雪松, 张晓春, 等. 山区高速公路驾驶人加减速行为建模[J]. 中国公路学报, 2020, 33(7): 167-175. CHEN Zhigui, WANG Xuesong, ZHANG Xiaochun, et al. Modeling of driver acceleration and deceleration behavior in mountain freeways[J]. China Journal of Highway and Transport, 2020, 33(7): 167-175. |
| [13] |
ZHU W X, ZHANG L D. Friction coefficient and radius of curvature effects upon traffic flow on a curved road[J].
Physica A: Statistical Mechanics and Its Applications, 2012, 391(20): 4597-4605.
DOI:10.1016/j.physa.2012.05.032 |
| [14] |
邓天民, 罗骁, 邵毅明, 等. 山区公路曲线路段汽车轨迹模式与切弯行为[J]. 东南大学学报(自然科学版), 2019, 49(2): 388-396. DENG Tianmin, LUO Xiao, SHAO Yiming, et al. Track patterns and curve cutting behavior on curved sections of mountain roads[J]. Journal of Southeast University (Natural Science Edition), 2019, 49(2): 388-396. |
| [15] |
陈莹, 王晓辉, 张晓波, 等. 山区公路回头曲线的车道偏移行为与自由行驶轨迹模型[J]. 交通运输工程学报, 2022, 22(4): 382-395. CHEN Ying, WANG Xiaohui, ZHANG Xiaobo, et al. Lane offset behavior and free driving trajectory model of hairpin curves of mountain roads[J]. Journal of Traffic and Transportation Engineering, 2022, 22(4): 382-395. |
| [16] |
戢晓峰, 谢世坤, 覃文文, 等. 基于轨迹数据的山区危险性弯道路段交通事故风险动态预测[J]. 中国公路学报, 2022, 35(4): 277-285. JI Xiaofeng, XIE Shikun, QIN Wenwen, et al. Dynamic prediction of traffic accident risk in risky curve sections based on vehicle trajectory data[J]. China Journal of Highway and Transport, 2022, 35(4): 277-285. |
| [17] |
PAL D, MALLIKARJUNA C. Analysis of the effect of variable lateral gap maintaining behavior of vehicles on traffic flow modeling[J].
Procedia Engineering, 2016, 142: 198-204.
DOI:10.1016/j.proeng.2016.02.032 |
| [18] |
柯愈明, 李洪霞. 基本型平曲线设计方法[J]. 公路交通技术, 2003, 19(3): 5-7, 26. KE Yuming, LI Hongxia. Design methods of basic flat curve[J]. Technocogy of Highway and Transport, 2003, 19(3): 5-7, 26. |
| [19] |
邱小平, 马丽娜, 周小霞, 等. 基于安全距离的手动—自动驾驶混合交通流研究[J]. 交通运输系统工程与信息, 2016, 16(4): 101-108, 124. QIU Xiaoping, MA Lina, ZHOU Xiaoxia, et al. The mixed traffic flow of manual-automated driving based on safety distance[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(4): 101-108, 124. |
| [20] |
张建旭, 胡帅, 金宏意. 人机混驾交通流事故预警换道决策及特性分析[J]. 公路交通科技, 2023, 40(11): 212-221, 236. ZHANG Jianxu, HU Shuai, JIN Hongyi. Lane-changing decision and characteristic analysis on accident warning of mixed traffic flow with human-driving and autonomous vehicle[J]. Journal of Highway and Transportation Research and Development, 2023, 40(11): 212-221, 236. DOI:10.3969/j.issn.1002-0268.2023.11.025 |
| [21] |
蒋阳升, 王思琛, 高宽, 等. 混入智能网联车队的混合交通流元胞自动机模型[J]. 系统仿真学报, 2022, 34(5): 1025-1032. JIANG Yangsheng, WANG Sichen, GAO Kuan, et al. Cellular automata model of mixed traffic flow composed of intelligent connected vehicles' platoon[J]. Journal of System Simulation, 2022, 34(5): 1025-1032. |
 2025, Vol. 42
2025, Vol. 42



 ,
,