扩展功能
文章信息
- 张建军, 李波, 刘婉莹, 易昭.
- ZHANG Jianjun, LI Bo, LIU Wanying, YI Zhao
- 基于熵权灰色关联法的沥青-集料黏附体系表面能评价
- Surface energy of asphalt-aggregate adhesion system based on entropy weight gray correlation method
- 公路交通科技, 2025, 42(7): 30-39
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(7): 30-39
- 10.3969/j.issn.1002-0268.2025.07.004
-
文章历史
- 收稿日期: 2023-03-28
2. 甘肃恒石公路检测科技有限公司, 甘肃 兰州 730070;
3. 兰州交通大学 土木工程学院, 甘肃 兰州 730070
2. Gansu Hengshi Highway Inspection Technology Co., Ltd., Lanzhou, Gansu 730070, China;
3. School of Civil Engineering, Lanzhou Jiaotong University, Lanzhou, Gansu 730070, China
沥青路面在服役过程中,常因沥青-集料界面黏附性较差而导致路面结构破坏,唧浆、坑槽、剥落等水损害现象频发,使沥青路面过早退出服役状态。沥青-集料界面黏附作用是影响沥青混凝土抗水损害的一个重要因素。针对沥青混合料水损害评价方法,现行规范《公路工程沥青及沥青混合料试验规程》(JTG E20—2011)中常用的传统水煮法、冻融劈裂试验、浸水马歇尔试验[1]等。传统的集料与沥青的黏附性能过程相对复杂。许多试验方法与测试手段均能评价沥青-集料系统的黏附特性,但由于沥青-集料系统界面黏附机理的复杂性,至今仍无统一的标准试验方法[2]。因此,从沥青、集料的特性入手,分析该体系在不同条件下的黏附机理,对解决路面水损坏的问题有重要意义。表面能方法由于其定量测定并解释沥青-集料体系中黏附性能及其机理而得到快速发展和广泛的应用前景[3]。基于集料与沥青表面能参数,计算二者表面能指标,能定量分析集料、沥青体系的黏附性能,且较为科学、客观。目前,国内外学者运用表面能理论比较不同沥青对沥青混合料黏附性进行了大量研究,Clint Miller与RaquelMorae[4-5]基于矿物和沥青的表面自由能测量的黏附功可以预测沥青混合物的耐久性,不同沥青-集料的黏结强度与表面性能普遍一致。并且少数矿物可以与一些固有抗剥离性的沥青形成热力学稳定的键。刘敏亚[6]从表面能理论出发论证沥青-集料体系的黏附, 描述水对沥青膜从矿料表面剥离的过程并量化。邓冲[7]通过运用表面能理论计算破碎砾石及沥青的表面能参数,通过添加不同含量的抗剥落剂验证表面能与水稳定试验的关联,证明了表面能理论可以评价沥青混合料中抗水损害性能。韩森[8]通过表面能参数计算沥青-集料体系的黏附功,发现沥青的极性分量越大、非极性分量越小越有利于沥青-集料体系的水稳定性。
表面能在验证沥青混合料体系抗水损害能力的过程中,需要结合大量指标进行判断。熵权法是一种基于指标可变性的客观赋权方法。作为一种客观的权重分配方法,可以有效地避免主观判断误差导致权重分析的影响。同时,基于熵权法和灰色关联分析,对各指标进行相关分析。灰色关联分析能够多维度甄选评价指标。其中灰色关联度分析是灰色系统理论中的重要组成部分,以分析不同因素之间的关联度。基于熵权法和灰色理论,袁勤等[9]建立了粉煤灰耐久性纤维混凝土综合评价方法。与单独使用抗压强度耐蚀系数的指标评价方法相比,避免了试块的耐久性仅因抗压强度的耐蚀系数相同而评价为相同的情况。陈长坤[10]采用灰色关联分析处理受灾数据,得到指标灰色关联系数,后用熵权法得到各项指标权重,通过熵权-灰色关联分析暴雨洪涝灾情,进行评估和分级。汪颖[11]基于改进灰色关联分析的暂降源识别法,提取时域内信号特征,以熵权法改进灰色关联分析模型,通过仿真和实测数据验证熵权灰色关联法的正确性和实用性。李晓宇[12]基于灰色关联分析和熵权法,准确的电池增量容量估计对于确保电动汽车中电池系统的高效和安全运行起着重要作用。程永春[13]基于熵权灰色关联分析发现沥青混合料的级配中,沥青混合料的力学性能影响较大粒径在限制区附近。熵权灰色关联法客观高效地对各指标进行筛选关联,为进一步评价沥青路面性能提供方法。
本研究基于表面自由能理论,选取5种不同岩石作为集料研究对象。通过柱状灯芯法、躺滴法测量得到集料、沥青的表面能参数,构建沥青-集料体系黏附模型及剥落模型,评价沥青混合料的抗水损害能力。结合工程实际中常用的冻融劈裂试验及浸水马歇尔试验进行验证,最后通过熵权灰色关联综合评价工程试验与表面能试验相似性及合理性,为研究集料与沥青体系的黏附性能和抗水损害能力提供了一种新思路,为沥青-集料体系黏附评价方法的研究提供参考。
1 表面能理论在恒定压力、温度的相同物相组成的体系中,增加一个单位的表面积所消耗的能量定义为表面自由能,使用符号γ表示材料的表面自由能[14],而体系中表面自由能的变化量为ΔG,通常,表面自由能由色散分量(γLW)和极性分量(γAB)构成,色散分量为非极性的范德华力,极性分量由极性酸分量(γ+)和极性碱分量(γ-)构成,通过研究发现,极性酸分量与极性碱分量的关系存在如式(1)的关联,因此构成表面自由能由3个表面能参数构成,通过式(2)表达。
| $ \gamma^{\mathrm{AB}}=2 \sqrt{\gamma^{+} \gamma^{-}}, $ | (1) |
| $ \gamma=\gamma^{\mathrm{LW}}+\gamma^{\mathrm{AB}}=\gamma^{\mathrm{LW}}+2 \sqrt{\gamma^{+} \gamma^{-}} 。$ | (2) |
接触角在表面物理化学中最重要的一个参数之一[15],其测试方法目前是表面能测试中发展最为成熟的一种方法,通过Young[16]提出的润湿模型不仅可计算固相材料的表面能参数,在材料的多相性及表面粗糙度的推算中也起到重要作用。
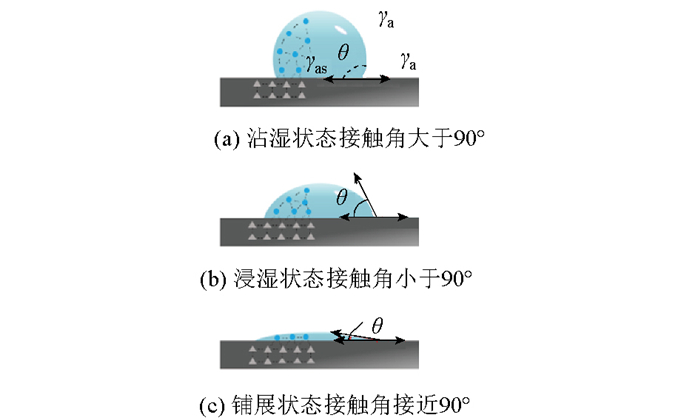
Young根据接触角大小的不同提出了3类润湿模型,如图 1所示,以90°为界限,接触角大于90°称为沾湿(不能润湿),接触角小于90°称为浸湿,接触角为0°称为铺展(润湿完全)。通过对润湿模型推理得到润湿的基本模型,称为Young方程,其中γa为沥青表面能,γs为集料表面能,γas为沥青与集料接触面上的界面能,如式(3)所示:
| $ \gamma_{\mathrm{a}} \cos \theta=\gamma_{\mathrm{s}}-\gamma_{\mathrm{as}}。$ | (3) |
|
| 图 1 3种润湿模型 Fig. 1 Three types of wetting models |
| |
结合对沥青混合料中黏附模型的确定,可通过接触角参数求得表面能参数,也就是经典的Young-Dupre方程,其中γaLW和γsLW分别为沥青和集料的色散分量,如式(4)所示。
| $ \begin{gathered} W_{\mathrm{as}}=\gamma_{\mathrm{a}}(1+\cos \theta)=2 \sqrt{\gamma_{\mathrm{a}}^{\mathrm{LW}} \gamma_{\mathrm{s}}^{\mathrm{LW}}}+2 \sqrt{\gamma_{\mathrm{a}}^{+} \gamma_{\mathrm{s}}^{-}}+ \\ 2 \sqrt{\gamma_{\mathrm{a}}^{-} \gamma_{\mathrm{s}}^{+}} 。\end{gathered} $ | (4) |
在不均匀体系中,至少存在2种相,各相间必然产生界面。因此,通过表面能理论研究沥青与集料体系的黏附性能时主要表现在2个方面,一方面是沥青与集料之间的黏附体系,在沥青混合料的拌和过程中,熔融态的沥青通过其自身的黏结作用附在集料表面,相当于液体在固体表面的润湿作用,在集料表面形成沥青-集料界面,通过对黏附功指标(Was)评价沥青黏附于集料表面的强度,而这个过程的黏附模型可通过式(5)表示,另一方面是在水的侵入作用导致形成的沥青与集料之间的剥落体系。道路在服役过程中受到外界环境的影响,导致小部分沥青从集料表面剥落,水通过剥落面侵入加速沥青从集料表面的脱落并扩大剥落面,因此通过剥落功(Wasw)评判有水状态下沥青集料剥落情况显得格外重要,剥落模型可通过式(6)表示。
| $ W_{\mathrm{as}}=2 \sqrt{\gamma_{\mathrm{a}}^{\mathrm{LW}} \gamma_{\mathrm{s}}^{\mathrm{LW}}}+2 \sqrt{\gamma_{\mathrm{a}}^{+} \gamma_{\mathrm{s}}^{-}}+2 \sqrt{\gamma_{\mathrm{a}}^{-} \gamma_{\mathrm{s}}^{+}}, $ | (5) |
| $ \begin{gathered} W_{\text {asw }}=2 \sqrt{\gamma_{\mathrm{a}}^{\mathrm{LW}} \gamma_{\mathrm{s}}^{\mathrm{LW}}}-2 \sqrt{\gamma_{\mathrm{a}}^{\mathrm{LW}} \gamma_{\mathrm{w}}^{\mathrm{LW}}}-2 \sqrt{\gamma_{\mathrm{w}}^{\mathrm{LW}} \gamma_{\mathrm{s}}^{\mathrm{LW}}}+ \\ 2 \sqrt{\gamma_{\mathrm{a}}^{+} \gamma_{\mathrm{s}}^{-}}+2 \sqrt{\gamma_{\mathrm{a}}^{-} \gamma_{\mathrm{s}}^{+}}-2 \sqrt{\gamma_{\mathrm{a}}^{+} \gamma_{\mathrm{w}}^{-}}-2 \sqrt{\gamma_{\mathrm{a}}^{-} \gamma_{\mathrm{w}}^{+}}- \\ 2 \sqrt{\gamma_{\mathrm{s}}^{+} \gamma_{\mathrm{w}}^{-}}-2 \sqrt{\gamma_{\mathrm{s}}^{-} \gamma_{\mathrm{w}}^{+}}, \end{gathered} $ | (6) |
式中,γ右下角的a代表沥青,s代表集料,w代表水。
2 试验材料及研究方法 2.1 原材料选取不同种类的石料,分别有A类石灰岩、B类石灰岩、玄武岩、花岗岩及辉绿岩5类。同时选择90#基质沥青制备沥青混合料,根据相关规范对沥青和5种集料进行基本性能测试,集料试验结果如表 1所示,沥青的试验结果如表 2所示。
| 集料种类 | 沥青黏附等级 | 吸水率/% | 压碎值/% | 洛杉矶磨耗/% | 抛光值 |
| A类石灰岩 | Ⅴ | 0.50 | 15.9 | 14.3 | 43 |
| B类石灰岩 | Ⅴ | 0.34 | 12.7 | 13.6 | 44 |
| 玄武岩 | Ⅳ | 0.60 | 11.3 | 12.4 | 42 |
| 花岗岩 | Ⅲ | 0.62 | 10.1 | 13.5 | 44 |
| 辉绿岩 | Ⅴ | 0.51 | 12.4 | 6.8 | 45 |
| 沥青种类 | 25 ℃针入度/(0.1 mm) | 软化点/℃ | 15 ℃延度/cm | 135 ℃布氏黏度/(mPa·s) |
| ZH 90# | 88.7 | 46.8 | >100 | ≤ 3 |
通过上述基本性能试验结果发现,本研究采用的沥青与石料的基本性能指标满足中国相关现行行业规范,但是不同岩石的黏附性等级却截然不同,花岗岩刚好满足沥青路面的技术要求,但其黏附性等级为Ⅲ级,在潮湿区和湿润区使用风险极大,因此定量研究各种石料的黏附性能显得格外重要。
2.2 表面能测试 2.2.1 沥青的表面能为得到沥青及沥青-集料体系的表面能参数,需要获取沥青、集料的表面自由能及分量数据,故用躺滴法测定沥青的表面能参数[17]。选取3类常温稳定性较好,不与沥青互溶的液体,包括蒸馏水、甘油和甲酰胺,设定测试液体滴定量3 μL,以0.5 μL/s的速率滴定在待测沥青试样上,抓拍到液滴滴定在沥青样品的画面,计算方法采用切线法测试,试样仅能用一种液体进行,每个试样至少测试3个以上不同位置,然后取平均值待所有液体测试完后,记录并保存测试数据,得到所测试沥青试样的接触角,最后基于Young-Dupre方程对沥青表面能参数进行计算。
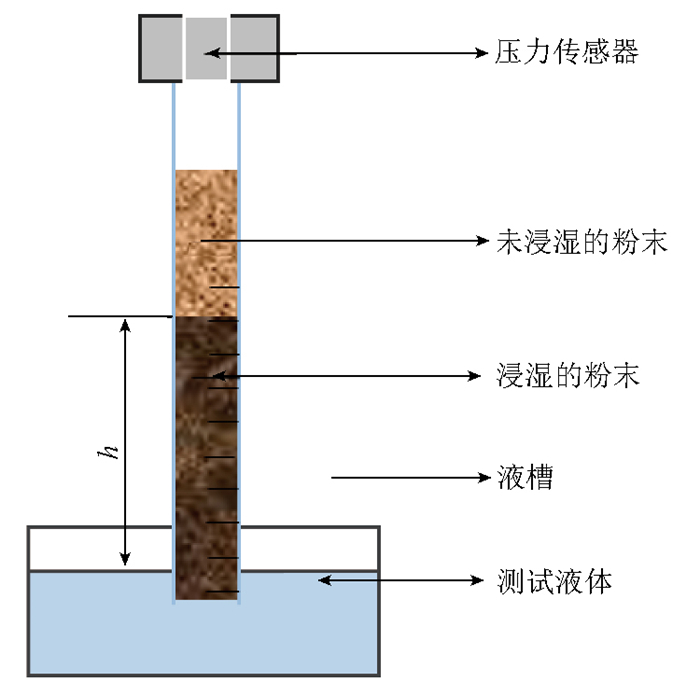
2.2.2 集料的表面能本研究采用表面能理论中的接触角法进行测试,通过柱状灯芯法测得接触角反算集料的表面能,柱状灯芯法如图 2所示,粉体于毛细玻璃管中堆积时,粉体颗粒间存在孔隙,当粉体粒度和堆积密度一定时,孔隙的尺寸将确定统计尺寸。由于这些孔隙形成的通道可以看作毛细管,若测试液体与毛细玻璃管中堆积的测试粉体接触,会出现毛细上升现象。
|
| 图 2 柱状灯芯法 Fig. 2 Column wicking method |
| |
本试验选用5种不同的岩石样品洗涤、干燥后研磨成粉。试验前,粉末样品和毛细管应在(105±5) ℃的烘箱中干燥,以防止石粉因高湿度而产生静电,无法均匀分布在毛细管玻璃管中。试验的具体操作如下:首先,将等量的石粉(0.6 g)放入毛细管(内径0.2 cm)中,用尼龙网覆盖底部(防止试验过程中骨料粉泄漏)并振实。在恒定高度下垂直方向自由下坠毛细管固定时间,达到最佳压实状态后放置在自制夹具板上。再将测试液体放置于置物台,打开信息捕捉系统,移动旋钮,使毛细管底部位于测试液体液面2 cm处。最后,等待测试流体通过毛细作用向上渗透。同时,收集试验数据并进行统计分析。
假设毛细管的半径为r,则液体上升的速度v可以表示为:
| $ v=\frac{\mathrm{d} h}{\mathrm{~d} t}=\gamma^2 \Delta P / 8 \eta h, $ | (7) |
式中,h为液体在粉柱中浸渍高度;ΔP为毛细管两端的压力差;η为液体的黏度;t为浸渍液体浸渍的时间。
液体上升的驱动力弯曲液面产生的压力差,从Laplace方程可知,压力差与接触角的关系可以表示为:
| $ \Delta P=\left(\frac{2 \gamma_{\mathrm{SV}} \cos \theta}{r}\right)+\Delta P_{\mathrm{c}}, $ | (8) |
式中,γSV表示海体与气体的界面表面能;ΔPc表示毛细玻璃管两端压力差(可忽略小计)。
当t=0,h=0时,方程可表示为:
| $ h^2=\left(r^2 / 4 \eta\right)\left[\left(\frac{2 \gamma_{\mathrm{SV}} \cos \theta}{r}\right)+\Delta P\right] t。$ | (9) |
通常毛细玻璃管两端的压力差ΔP很小,特别是当h<10 cm时可以忽略,本试验中石料粉体的填充高度小于8 cm,因此可以将等式简化得到:
| $ \frac{h^2}{t}=\frac{\gamma_{\mathrm{SV}} r\text{cos} \;\theta}{2 \eta} 。$ | (10) |
通过浸润高度平方及浸润时间的比值h2/t可计算得到相应石粉的接触角值,运用Young方程可计算得到集料表面能参数值。
2.3 试验数据处理 2.3.1 熵权分析方法熵权法是通过将试验结果赋予相应的权重,基于熵权法对宏观水稳定性试验统筹分析,选择MS0,TSR宏观水稳定性指标和各表面能参数指标为对比指标,按文献中相应步骤计算得到各指标相应权重系数,并与标准化处理后的矩阵进行计算得到综合评价指标Wi,其计算公式如下:
| $ W_i=\sum\limits_{j=1}^n \omega_j Y_{i j}, $ | (11) |
式中,ωj为指标权重系数;Yij为原始数据标准化后的数据矩阵。
2.3.2 灰色关联理论灰色关联分析可用于各种因素的关联分析。这是一种基于因素趋势相似性的相关性计算算法。变化趋势与各种因素之间的相关性成正比。灰色关联度理论可在信息条件不充分的情况下耦合分析,为数据分析提供更优的可行性[18-19]。
具体方法是建立参考数据列和对比数据列,通过无量纲化处理计算灰色关联系数ξ,其计算公式见式(12);计算灰色关联度ri,其计算公式见式(13);其次可通过权重系数计算基于熵权法的灰色关联度进行比较,计算方法见式(14),其中2个参数φi和ri的值越大表明比较数列与参考数列之间的相关性越强。
| $ \begin{gathered} \xi\left(x_0(k), x_i(k)\right)= \\ \frac{\min\limits_i \min\limits _k\left|x_0(k), x_i(k)\right|+\rho \max\limits _i \max\limits _k\left|x_0(k), x_i(k)\right|}{\left|x_0(k), x_i(k)\right|+\rho \max\limits _i \max\limits _k\left|x_0(k), x_i(k)\right|}, \end{gathered} $ | (12) |
式中,x0(k)为参考数列的无量纲化结果;xi(k)为比较数列的无量纲化结果;ρ为区分系数,一般取0.5。
| $ r_i=\frac{\sum\limits_{k=1}^n \xi\left(x_0(k), x_i(k)\right)}{n}, $ | (13) |
| $ \varphi_i=\sum\limits_{k=1}^n \omega_j \times \xi\left(x_0(k), x_i(k)\right)。$ | (14) |
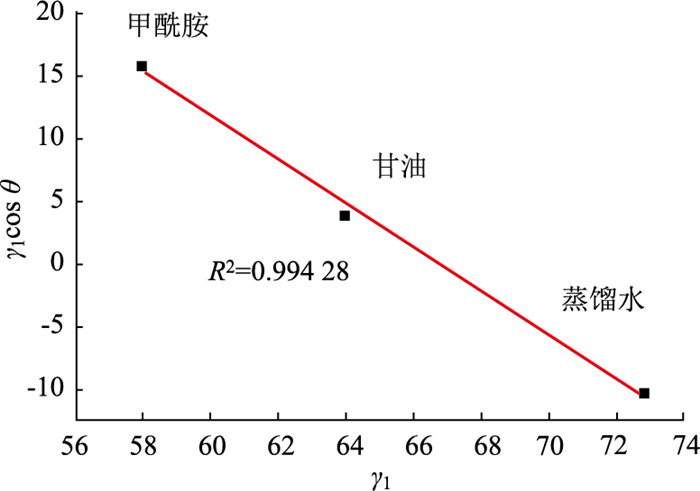
根据2.2.2节躺滴法的操作步骤,在德国东方德菲OCA25型视频光学接触角测量仪上对沥青试样进行测试,为确保测试结果的可靠性,便于试验横向对比,设定4次平行试验并以平均接触角数值作为最终结果,其结果如表 3所示,为检验接触角参数的有效性,需对不同测试液体的表面能γl与γl cos θ线性关系验证[20],如图 3所示。
| 试剂 | 蒸馏水 | 甘油 | 甲酰胺 |
| 平均接触角值/(°) | 98.36 | 86.38 | 74.14 |
| 变异系数/% | 0.24 | 0.4 | 0.36 |
|
| 图 3 不同测试液体的表面能γl与γlcos θ的线性拟合 Fig. 3 Linear fitting of surface energy γl and γl cos θ for different reagents |
| |
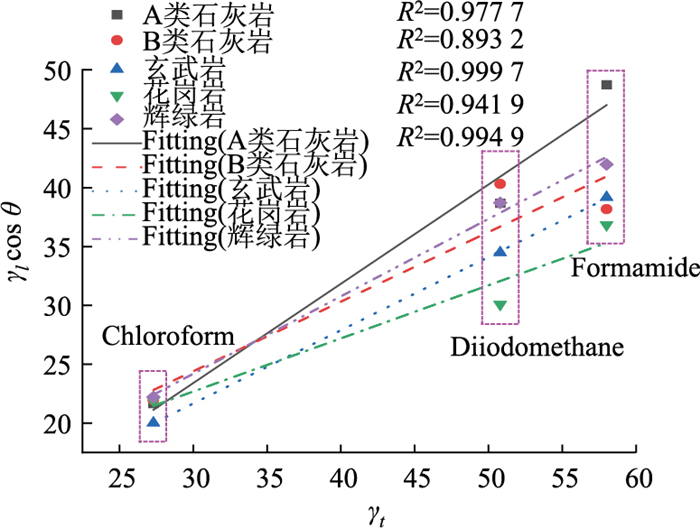
从图 4中可以看出,拟合结果的决定系数R2为0.994 28,表明γl与γlcos θ存在极好的线性关系,因此可以说明试验测得接触角数据具有可靠性。进一步将接触角数据代入Young-Dupre方程进行计算,得到沥青表面能参数,如表 4所示。
|
| 图 4 5种集料接触角线性拟合关系 Fig. 4 Linear fitting relation of contact angle of 5 types of aggregates |
| |
| 表面能参数 | γa | γaLW | γaAB | γa+ | γa- |
| ZH 90# | 40.49 | 39.38 | 1.11 | 0.89 | 0.343 |
3.1.2 集料接触角与表面能
按照2.3节测试及计算方法对5种不同集料表面能进行柱状灯芯法测试,计算浸润高度平方及浸润时间的比值h2/t。试验前,对不同集料在毛细玻璃管中形成的有效半径进行标定,标定液体选择表面能较小的戊烷; 试验开始,通过6种不同浸渍液体组合进行试验,通过线性拟合关系验证,得到最佳一类液体组合,包括有氯仿、二碘甲烷、甲酰胺3种浸渍液体,通过式(10)计算得到相应液体的接触角,见表 5。
| 试剂 | 接触角/(°) | ||||
| A类石灰石 | B类石灰石 | 玄武岩 | 花岗岩 | 辉绿岩 | |
| 甲酰胺 | 32.84 | 48.84 | 47.51 | 50.58 | 43.66 |
| 二碘甲烷 | 40.41 | 37.48 | 47.26 | 53.69 | 40.36 |
| 氯仿 | 37.52 | 36.44 | 42.86 | 36.55 | 35.54 |
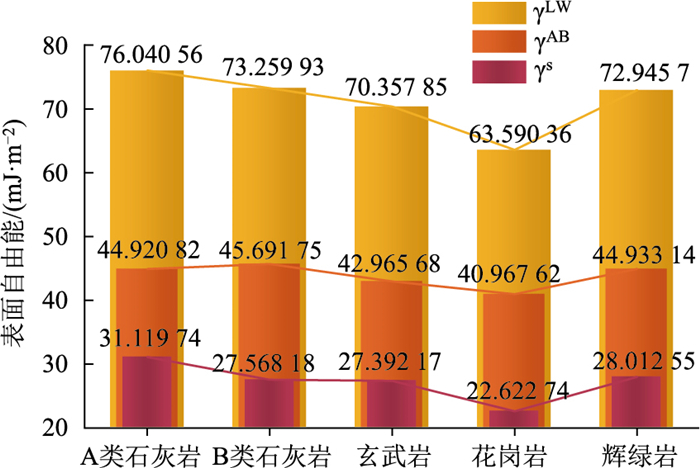
从图 4中可以看出,不同测试液体的表面能γl与γlcos θ线性拟合程度非常高,通过验证5种集料的接触角数值后,进行表面能参数的计算,为更清晰比较各集料的表面能参数将数据绘图处理。从图 5中可以看出,5种不同集料的表面能的大小为A类石灰岩、辉绿岩、B类石灰岩、玄武岩、花岗岩,组成表面能的极性分量和表面能大小比较呈相同趋势,在集料表面能中,色散分量占比较多,占60%左右,其中花岗岩色散分量占比最多,达到64.4%。
|
| 图 5 5类集料的表面能参数 Fig. 5 Surface energy parameters of 5 types of aggregates |
| |
3.2 沥青-集料体系黏附功与剥落功
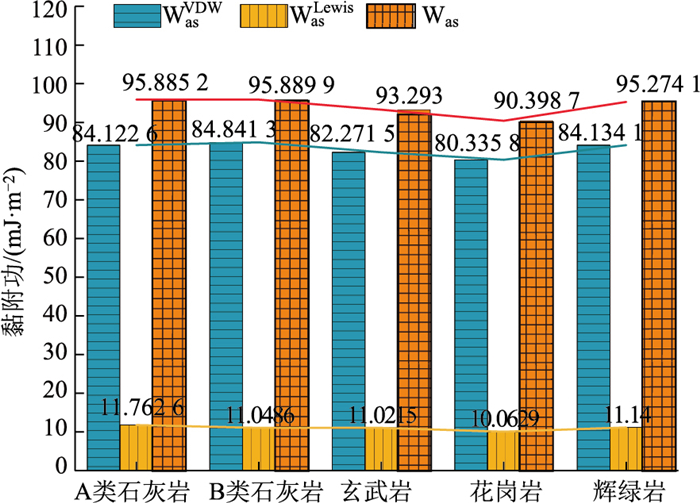
结合前文对沥青与集料表面能参数的计算结果,通过式(3)和式(4)的沥青-集料体系黏附模型和剥落模型进行计算,计算其与沥青之间形成的黏附功和剥落功,其中VDW黏附功为沥青和集料范德华力形成的黏附功,也就是色散分量形成的黏附功,Lewis黏附功为沥青与集料的路易斯酸碱形成的黏附功。为更清晰比较各沥青-集料之间剥落功的大小,取Gibbs自由能变化量进行作图,其数值为各剥落功数值的绝对值,最终结果如图 6和图 7所示。
|
| 图 6 5类沥青-集料体系的黏附功参数 Fig. 6 Adhesion work parameters of 5 asphalt-aggregate systems |
| |

|
| 图 7 5类沥青-集料体系的剥落功参数 Fig. 7 Spalling work parameters of 5 asphalt-aggregate systems |
| |
其中图 6和图 7中VDW黏附功和VDW剥落功分别为沥青和集料范德华力形成的黏附功和剥落功,也就是色散分量形成的黏附功,Lewis黏附功和Lewis剥落功分别为沥青与集料的路易斯酸碱形成的黏附功和剥落功。
通过图 6的数据比较发现,5种不同集料与沥青产生的黏附功大小排序:B类石灰岩、A类石灰岩、辉绿岩、玄武岩、花岗岩,而5类岩样的剥落功变化趋势与黏附功变化趋势一致,但其中VDW剥落功与其他参数的变化趋势恰恰相反。从图 7中还可以发现,黏附功中VDW黏附功占主导作用,占总黏附功87%左右;而剥落功中,占主要贡献量的是Lewis剥落功,占到总剥落功的68%左右;而VDW剥落功只占到30%左右。可能是由于有强极性水的参与后,使得沥青与集料界面处黏结能力中占有主导作用的范德华力降低,而究其原因,是强极性水的参与使得范德华力中占主导作用的色散力降低,数值较小的取向力成为主导,而又因为诱导力通常很小,因此导致体系中总体的范德华力降低。
在相同沥青构成的不同沥青-集料体系中,由于集料表面能参数影响体系中黏附功参数,表面能越大,黏附功越大,抗水损害能力越强,因此在实际工程中应选择表面能参数较高的集料,可提升沥青路面的抗水损害能力。
3.3 沥青-集料体系表面能参数及其混合料水稳定性指标关联性分析 3.3.1 水稳定性直观评价前文运用表面能理论,对沥青-集料体系进行表面能参数计算,为进一步验证表面能理论的可靠性和可行性,选取行业规范推荐的试验方法,包括有浸水马歇尔试验及冻融劈裂试验,将石料与沥青拌和成5种不同混合料后开展水稳定性能试验,并确定水稳定性能指标。
试验中沥青混合料采用的粗集料及细集料都是相同岩性的,矿粉采用的相同岩性大粒径的集料研磨而成,粒径小于0.075 mm,选用的级配类型为AC-13中值级配,通过严格控制沥青混合料中的石料不同,其他材料、级配和油石比(5%)高度相同,确保混合料中可变的因素只有石料,按照上述要求通过马歇尔成型方法进行马歇尔试件的制作,完成水稳定性试验。
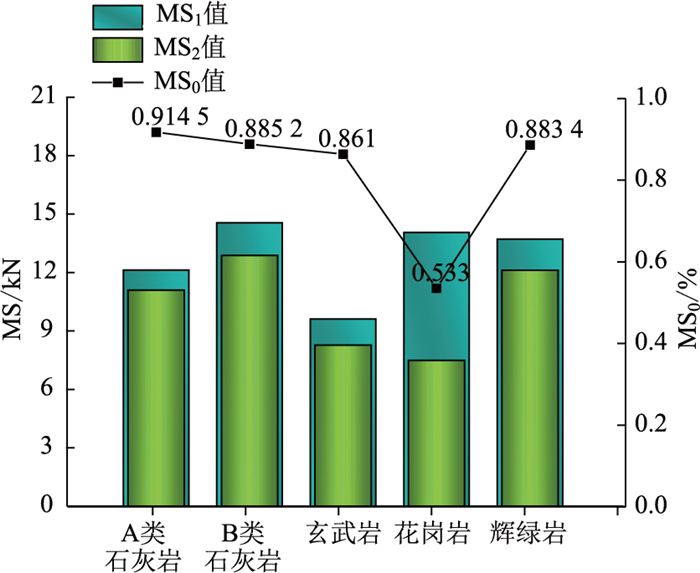
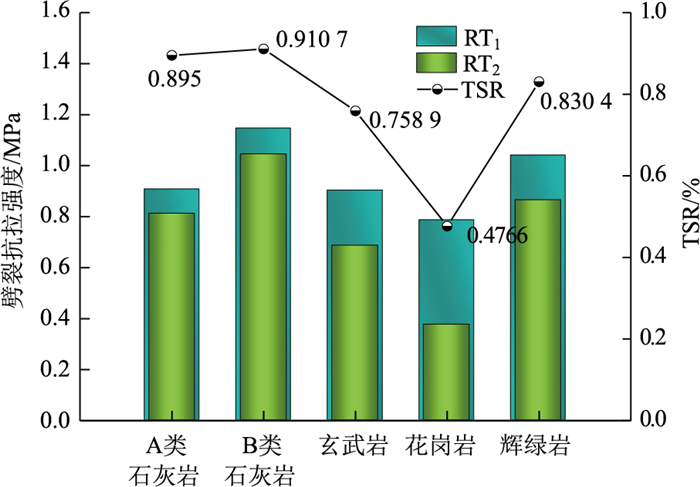
浸水马歇尔试验中,MS0指试件的浸水残留稳定度(%);MS1指试件的稳定度(kN);MS2指试件浸水48 h后的稳定度(kN)。冻融劈裂试验中TSR指冻融劈裂强度比(%),RT1指第1组单个试件的劈裂抗拉强度(MPa);RT2指第2组单个试件的劈裂抗拉强度(MPa)。
试验结果如图 8和图 9所示,从图中可以看到,花岗岩的稳定度相对其他4种岩石来说是相对较高的,达到了14.06 kN,而浸水48 h后的稳定度下降了46.7%,导致浸水残留稳定度为53.3%,完全不满足规范要求。其他的岩石都满足现行规范要求,因此,在沥青混合料中选择石料岩性时,应避免使用花岗岩类岩石,其他4类从大到小排序为:B类石灰岩、A类石灰岩、辉绿岩、玄武岩。花岗岩的主要成分为SiO2,根据汪海年[2]及SUN[21]研究发现,SiO2的界面能远低于其他金属氧化的原因是SiO2与沥青界面的黏结主要依靠分子间的范德华力,作用力较小。
|
| 图 8 浸水马歇尔试验结果 Fig. 8 Immersion Marshall test result |
| |
|
| 图 9 冻融劈裂试验结果 Fig. 9 Freeze-thaw splitting test result |
| |
经过试验验证花岗岩不满足规范要求,且相差甚远。因此不宜在湿润且寒冷地区使用该花岗岩作为沥青路面的石料用料,其他4类岩石的冻融劈裂强度比从大到小排序为:B类石灰岩、A类石灰岩、辉绿岩、玄武岩。整体来说,两类石灰岩的浸水残留稳定度及冻融劈裂强度比都大于玄武岩和辉绿岩,二者数值相差不大,总体来说冻融劈裂试验结果与浸水马歇尔试验结果基本一致,且与表面能参数排序一致,验证了本研究对表面能参数指标评价沥青混合料水稳定性的可行性。
3.3.2 熵权灰色关联分析本节运用普通灰色关联分析及熵权灰色关联分析对各表面能参数指标筛选优化,再分别通过熵权法综合分析法从表面能评价指标和工程试验指标MS0、TSR这2个方面评价5类集料的综合评价分,从而分析比较表面能参数指标与水稳定性能参数指标的相关程度。
沥青混合料MS0和TSR作为参考序列,选择集料表面能参数、体系中VDW黏附功、Lewis黏附功、总黏附功、VDW剥落功、Lewis剥落功、总剥落功作为对比列,分别用γs,Was-VDW,Was-Lewis,Was,Wasw-VDW,Wasw-Lewis表示,见表 6和表 7。
| 计算参数 | 指标熵Hj | 权重ωj | 灰色关联度ri | 熵权法灰色关联度φi |
| MS0值 | 0.449 3 | 0.112 5 | — | — |
| γsAB | 0.476 9 | 0.106 9 | 0.778 0 | 0.083 2 |
| γsLW | 0.476 8 | 0.106 9 | 0.804 7 | 0.086 0 |
| γs | 0.466 0 | 0.109 1 | 0.869 8 | 0.094 9 |
| Was-VDW | 0.475 9 | 0.107 1 | 0.788 7 | 0.084 5 |
| Was-Lewis | 0.476 8 | 0.106 9 | 0.847 1 | 0.090 6 |
| Was | 0.467 5 | 0.108 8 | 0.803 9 | 0.087 5 |
| Wasw-VDW | 0.717 7 | 0.057 7 | 0.769 7 | 0.044 4 |
| Wasw-Lewis | 0.461 2 | 0.110 1 | 0.874 6 | 0.096 3 |
| Wasw | 0.638 8 | 0.073 8 | 0.839 7 | 0.062 0 |
| 计算参数 | 指标熵Hj | 权重ωj | 灰色关联度ri | 熵权法灰色关联度φi |
| TSR值 | 0.458 3 | 0.110 9 | — | — |
| γsAB | 0.476 9 | 0.107 1 | 0.799 0 | 0.085 6 |
| γsLW | 0.476 8 | 0.107 1 | 0.772 0 | 0.082 7 |
| γs | 0.466 0 | 0.109 3 | 0.783 4 | 0.085 7 |
| Was-VDW | 0.475 9 | 0.107 3 | 0.752 4 | 0.080 7 |
| Was-Lewis | 0.476 8 | 0.107 1 | 0.771 0 | 0.082 6 |
| Was | 0.467 5 | 0.109 0 | 0.752 5 | 0.082 0 |
| Wasw-VDW | 0.717 7 | 0.057 8 | 0.724 6 | 0.041 9 |
| Wasw-Lewis | 0.461 2 | 0.110 3 | 0.764 7 | 0.084 4 |
| Wasw | 0.638 8 | 0.074 0 | 0.750 1 | 0.055 5 |
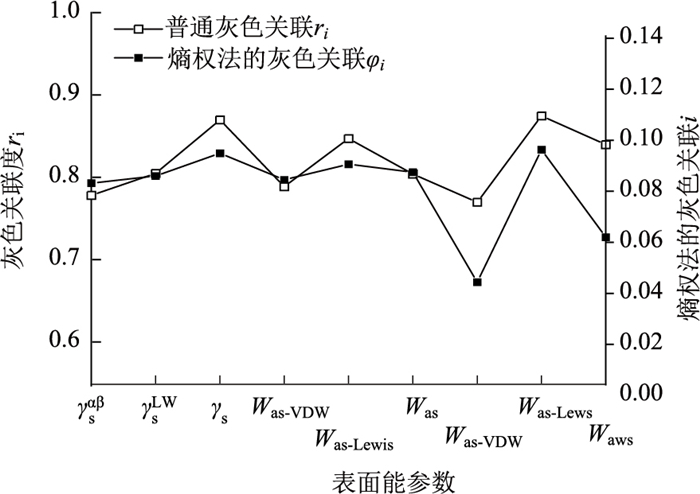
通过对熵权法的灰色关联度φi和普通灰色关联度ri计算,为更清晰比对计算结果,对数据进行绘图处理,如图 10和图 11所示,进行指标相关度排序,其中关联度越大表明子序列与母序列几何形态趋于一致,即与MS0和TSR的关联程度较强。
|
| 图 10 表面能参数与浸水残留稳定度的灰色关联度 Fig. 10 Grey correlation between surface energy and water immersion residual stability |
| |

|
| 图 11 表面能参数与TSR的灰色关联度 Fig. 11 Grey correlation between surface energy and TSR |
| |
从图 10、图 11中能够更清晰地区分表面能参数与MS0、TSR的关联度,可以发现,基于熵权法的灰色关联度φi和普通灰色关联ri的相关度排序趋势基本一致,证明了熵权法的灰色关联的可靠性,与普通灰色关联度相比,熵权灰色关联度能够更好的比较出各项表面能参数与MS0、TSR的关联程度,与MS0的关联程度排序为:Wasw-Lewis>γs>Was-Lewis>Was>γsLW>Was-VDW>γsAB>Wasw>Wasw-VDW,与TSR的关联程度排序为:γs>γsAB>Wasw-Lewis>γsLW>Was-Lewis>Was>Was-VDW>Wasw>Wasw-VDW。结合普通灰色关联度分析及熵权灰色关联综合分析,结果表明γs与MS0、TSR相关程度最高,其次为Wasw-Lewis,表明影响沥青混合料抗水损害能力的主要因素为集料表面能及极性分量产生的黏附功和剥落功,而Was-VDW与Wasw-VDW的关联度数值之和最低,因此将表面能参数进行优化筛选,去除这两个表面能指标进行熵权法综合分析。
3.4 基于熵权灰色关联的沥青-集料体系黏附性评价通过对MS0,TSR等工程指标数据进行标准化处理,按照熵权法的计算步骤对各个指标权重系数进行计算,按式(4)计算综合评价指标Wi,为参照组,通过灰色关联法得到表面能参数的关联度,舍去2个相关性最低的Was-VDW和Wasw-VDW参数,按相同的计算方法对其余表面能参数指标进行综合评价指标的计算,包含有γsAB,γsLW,γs,Was-Lewis,Was,Wasw-Lewis,为对比组,通过对比参照组和对比组可以得到两个数据组的相关性,计算结果如图 12所示。

|
| 图 12 参照组与对比组的结果对比 Fig. 12 Reference group v.s. comparison group |
| |
通过对两组综合分析数据的比对结果绘图,可以明显看出2组数据的变化趋势相同,排序统一,评分从大到小为:A类石灰岩、B类石灰岩、辉绿岩、玄武岩、花岗岩,其中综合评分最高的是A类石灰岩,宏观黏结性试验的参照组中的综合评分为0.987,在表面能参数试验的对比组中,综合评分也是最高的0.751 1。综合评分最差的为花岗岩,花岗岩在参照组中的评分为0,而在对比组里评分为0.232 1,因此可以看出用表面能指标替代工程水稳定性试验具有可行性和实用性[22]。
4 结论(1) 通过表面能理论研究可以发现,不同集料表面能数值不同,表面能数值越大,其沥青-集料体系的黏附功也就越大,构成的沥青混合料抗水损害能力越强,这同时也验证了计算不同集料表面能参数分析沥青混合料抗水损害能力的可行性与必要性。
(2) 通过普通灰色关联法和熵权灰色关联法分析得到,在多个表面能参数中,色散分量计算得到的VDW黏附功和VDW剥落功与MS0,TSR相关程度最小。因此,在使用相同沥青的条件下,极性分量相较于色散分量对沥青混合料抗水损害能力影响较大。
(3) 提出了一种基于熵权灰色关联法的综合评价法对5种不同集料进行分析,分别采用表面能指标和MS0、TSR工程水稳定性试验指标比对,发现综合评价指标的变化趋势高度一致,且呈正相关,说明表面能指标替代工程水稳定性试验分析沥青混合料抗水损害能力的方法具有可行性和实用性。
(4) 本工作主要在试验阶段用表面能对沥青-集料体系黏附性能进行评价。为了更准确地反映工程实际,在后续工作中还需进一步对研究方法进行完善。熵权法赋权依赖于样本,得到的各指标权重会随样本的变化而改变,仅用熵权法求权评标不能保证得出最合理的结果,可以综合考虑多种方法结合赋权。
| [1] |
马祥辉, 杨振宇, 樊亮, 等. 基于界面黏附理论的沥青与集料黏附特性研究进展[J]. 合成材料老化与应用, 2021, 50(6): 108-111, 33. MA Xianghui, YANG Zhenyu, FAN Liang, et al. Research progress on adhesion characteristics of asphalt and aggregates based on interfacial adhesion theory[J]. Synthetic Materials Aging and Application, 2021, 50(6): 108-111, 33. |
| [2] |
汪海年, 许卉, 王江峰, 等. 集料理化特性对沥青-集料界面黏附性能的影响[J]. 长安大学学报(自然科学版), 2022, 42(3): 52-61. WANG Hainian, XU Hui, WANG Jiangfeng, et al. Influence of aggregate physicochemical properties on interfacial adhesion performance of asphalt-aggregate[J]. Journal of Chang 'an University (Natural Science Edition), 2022, 42(3): 52-61. |
| [3] |
GU J C, CHEN T Y, XIAO P, et al. Constructing oxidized carbon spheres-based heterogeneous membrane with high surface energy for energy-free water purification[J]. Chemical Engineering Journal, 2022, 431(P2).(2021-12-18)[2023-03-27]. https://doi.org/10.1016/j.cej.2021.134132.
|
| [4] |
MILLER C, LITTLE D N, BHASIN A, et al. Surface energy characteristics and impact of natural minerals on aggregate-bitumen bond strengths and asphalt mixture durability[J].
Transportation Research Record, 2012, 2267(1): 45-55.
|
| [5] |
MORAES R, VELASUEZ R, BAHIA H. Using bond strength and surface energy to estimate moisture resistance of asphalt-aggregate systems[J].
Construction and Building Materials, 2017, 130: 156-170.
|
| [6] |
刘亚敏, 韩森, 李波. 基于表面能理论的沥青与矿料黏附性研究[J]. 建筑材料学报, 2010, 13(6): 769-772. LIU Yamin, HAN Sen, LI Bo. Research on adhesion between asphalt and aggregate based on surface energy theory[J]. Journal of Building Materials, 2010, 13(6): 769-772. |
| [7] |
邓冲, 罗蓉, 张德润. 基于表面能理论的破碎砾石沥青混合料水稳定性定量分析[J]. 公路交通科技, 2020, 37(7): 17-23. DENG Chong, LUO Rong, ZHANG Derun. Quantitative analysis on water stability of asphalt mixture with crushed gravel based on surface energy theory[J]. Journal of Highway and Transportation Research and Development, 2020, 37(7): 17-23. |
| [8] |
韩森, 刘亚敏, 徐鸥明, 等. 材料特性对沥青-集料界面粘附性的影响[J]. 长安大学学报(自然科学版), 2010, 30(3): 6-9, 70. HAN Sen, LIU Yamin, XU Ouming, et al. Influence of material characteristics on adhesion at interface between asphalt and aggregate[J]. Journal of Chang 'an University (Natural Science Edition), 2010, 30(3): 6-9, 70. |
| [9] |
刘秀, 李文洋. 基于熵权物元可拓模型的路堑边坡安全性评价[J]. 公路交通科技, 2022, 39(11): 49-55. LIU Xiu, LI Wenyang. Evaluation on safety of cutting slope based on entropy weight matter-element extension model[J]. Journal of Highway and Transportation Research and Development, 2022, 39(11): 49-55. |
| [10] |
QIN Y, GUAN K, KOU J L, et al. Durability evaluation and life prediction of fiber concrete with fly ash based on entropy weight method and grey theory[J]. Construction and Building Materials, 2022, 327: 126918. (2022-04-11)[2023-03-27].https://doi.org/10.1016/j.conbuildmat.2022.126918.
|
| [11] |
陈长坤, 孙凤琳. 基于熵权-灰色关联度分析的暴雨洪涝灾情评估方法[J]. 清华大学学报(自然科学版), 2022, 62(6): 1067-1073. CHEN Changkun, SUN Fenglin. Flood damage assessments based on entropy weight-grey relational analyses[J]. Journal of Tsinghua University(Science and Technology), 2022, 62(6): 1067-1073. |
| [12] |
汪颖, 王欢, 王昕. 一种基于改进灰色关联分析的电压暂降源识别方法[J]. 电测与仪表, 2020, 57(15): 1-7. WANG Ying, WANG Huan, WANG Xin. A method of voltage sag source identification based on improved grey relational analysis[J]. Electrical Measurement and Instrumentation, 2020, 57(15): 1-7. |
| [13] |
程永春, 李赫, 李立顶, 等. 基于灰色关联度的矿料对沥青混合料力学性能的影响分析[J]. 吉林大学学报(工学版), 2021, 51(3): 925-935. CHENG Yongchun, LI He, LI Liding, et al. Analysis of mechanical properties of asphalt mixture affected by aggregate based on grey relational degree[J]. Journal of Jilin University (Engineering and Technology Edition), 2021, 51(3): 925-935. |
| [14] |
OUYANG G, WANG C X, YANG G W. Surface energy of nanostructural materials with negative curvature and related size effects[J].
Chemical Reviews, 2009, 109(9): 4221-4247.
|
| [15] |
孙吉书, 于水, 许宁乾, 等. 考虑老化作用的沥青-集料界面黏附性评价[J]. 公路交通科技, 2019, 36(11): 1-7, 16. SUN Jishu, YU Shui, XU Ningqian, et al. Evaluation of asphalt aggregate interface adhesion considering aging effect[J]. Journal of Highway and Transportation Research and Development, 2019, 36(11): 1-7, 16. |
| [16] |
YOUNG T. An essay on the cohesion of fluids[J].
Philosophical Transactions of the Royal Society of London, 1832(1): 171-172.
|
| [17] |
杨松, 马泽慧, 王磊, 等. 躺滴法测量干湿循环条件下土壤固-液接触角的滞后特性[J]. 农业工程学报, 2018, 34(2): 114-119. YANG Song, MA Zehui, WANG Lei, et al. Hysteresis characteristics of soil solid-liquid contact angle measured by sessile drop method during wetting-drying cycles[J]. Transactions of the Chinese Society of Agricultural Engineering, 2018, 34(2): 114-119. |
| [18] |
刘轶华, 马利华, 苑洋. 基于灰色模糊的大桥对附近码头能力损失的研究[J]. 重庆交通大学学报(自然科学版), 2020, 39(7): 108-113. LIU Yihua, MA Lihua, YUAN Yang. Bridge to nearby wharf capacity loss based on grey fuzzy[J]. Journal of Chongqing Jiaotong University (Natural Science), 2020, 39(7): 108-113. |
| [19] |
ZU X H, YANG C L, WANG H C, et al. An EGR performance evaluation and decision-making approach based on grey theory and grey entropy analysis[J/OL]. Plos One, 2018, 13(1): e0191626.(2018-01-29)[2023-03-27]. https://doi.org/10.1371/journal.pone.0191626.
|
| [20] |
张华, 李海兵, 赵凤婷, 等. 磷矿粉末接触角测定方法研究与应用[J]. 化工矿物与加工, 2020, 49(5): 22-24. ZHANG Hua, LI Haibing, ZHAO Fengting, et al. Study and application of determination method of contact angle of phosphate powder[J]. Industrial Minerals and Processing, 2020, 49(5): 22-24. |
| [21] |
SUN Z L, LI S T, ZHANG J H, et al. Adhesion of bituminous crack sealants to aggregates using surface energy theory[J].
Journal of Materials in Civil Engineering, 2020, 32(10).
DOI:10.1061/(ASCE)MT.1943-5533.0003406 |
| [22] |
ZAIDI S B A, AIREY G D, GRENFELL J, et al. Moisture susceptibility assessment of hydrated lime modified asphalt mixture and surface energy[J].
International Journal of Pavement Engineering, 2022, 23(3): 599-611.
|
 2025, Vol. 42
2025, Vol. 42



 ,
,