扩展功能
文章信息
- 杜凯, 史晴晴, 李乐天, 宋京妮, 肖梅, 陈丹.
- DU Kai, SHI Qingqing, LI Letian, SONG Jingni, XIAO Mei, CHEN Dan
- 融合机器学习与可解释算法的货车燃油效率预测
- Truck fuel efficiency prediction integrating machine learning and interpretable algorithms
- 公路交通科技, 2025, 42(7): 202-213
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(7): 202-213
- 10.3969/j.issn.1002-0268.2025.07.021
-
文章历史
- 收稿日期: 2024-11-11
2. 长安大学 运输工程学院, 陕西 西安 710064;
3. 长安大学 长安都柏林国际交通学院, 陕西 西安 710064
2. School of Transportation Engineering, Chang'an University, Xi'an, Shaanxi 710064, China;
3. Chang'an Dublin International College of Transportation, Chang'an University, Xi'an, Shaanxi 710064, China
作为高碳排放行业,交通运输业碳排放量总体呈现增长趋势[1]。在碳达峰战略背景下,交通运输业节能减排尤为迫切,构建完善的排放监测系统对提升燃油效率及推动节能减排具有重要作用[2]。Li[3]研究表明,2019年中国交通运输业碳排放占比约为全国总数的11.0%,其中,公路运输占86.76%,而货车的碳排放量占公路运输总排放量的54.0%。因此,准确预测货车燃油效率并分析其影响因素对优化驾驶行为和促进节能减排具有重要意义。
国内外学者对车辆燃油消耗因素进行了深入研究,普遍认为油耗和排放水平由多因素共同作用形成。Zhou[4]研究了影响燃油经济性的主要因素,包括驾驶、天气、车辆、道路、交通及司机的特征。Díaz-Ramirez[5]通过生态驾驶培训试验,发现驾驶员的经验、驾驶错误、平均速度和载重比等与油耗高度相关。Yao[6]利用手机和OBD数据研究驾驶行为对燃料消耗的影响,建立的预测模型显示,平均速度、除停歇外的平均速度、平均加速度、减速时间百分比等是燃料消耗评估的重要指标。程颖[7]研究表明,不良驾驶行为, 如超长怠速和过急减速, 显著增加大型货车油耗,减少这2种行为的节油潜力分别可达2.6%和3.8%。马荣影[8]研究结果表明,车辆运行油耗与车辆运行状态参数之间的线性特征并不明显,而更适合于建立非线性回归模型。Fan[9]通过独立成分分析评估实验室与实际驾驶条件下燃油消耗差异的主要因素。He[10]通过实地测量分析轻型乘用车(包括汽油车、柴油车和混合动力车)的实际驾驶排放与燃油消耗,发现冷启动和道路坡度对排放和油耗有显著影响。姜壁刚[11]研究道路坡度对轻型柴油车二氧化碳排放的影响。Gong[12]通过建立二元logistic回归模型,系统研究了显著性因素对油耗的影响。关于油耗影响因素的研究大多数集中在探讨因素与油耗之间的关系,但并未深入分析因素之间的交互作用对油耗的影响机制。
在车辆油耗预测方面,车辆油耗预测方法大致可以分为2类:一类是基于车辆动力学原理构建的物理燃油消耗预测模型;另一类是数据驱动的燃油消耗预测模型[13]。第1类模型主要利用车辆内部结构的数学公式和组件工作原理构建,如引擎的物理或化学过程,以提供准确的预测结果[14]。例如,Peng[15]开发了一个基于引擎的校正模型,用于预测重型柴油卡车的燃料消耗,结果显示,模型在拟合优度和样本外预测性能方面优于弗吉尼亚理工微尺度能量与排放模型和综合模态排放模型。Huang[16]利用在简单道路条件下获得的数据,使用传统的微观模型来预测车辆燃料消耗。物理模型在预测瞬时燃油消耗方面表现优秀,但开发物理模型需要投入大量资源和时间,因此成本相对较高。第2类模型主要依赖传感器和其他车载设备获取丰富的与燃料消耗相关的车辆运行数据。通过挖掘数据中的优质特征,建立数据与燃料消耗之间的非线性联系,实现对燃油消耗的预测。相对于传统的物理模型,数据驱动模型更易构建,能够自动执行繁琐任务,保持准确性。在油耗预测中广泛使用的数据模型包括随机森林和支持向量机等机器学习模型,及反向传播神经网络、循环神经网络、长短期记忆(LSTM)等深度学习方法。师国东[17]提出了基于XGBoost-MSIWOA-LSTM的车辆油耗优化预测模型。Fan[18]研究重型卡车燃油消耗与车辆质量的非线性关系,并提出结合车辆质量的深度学习模型(LSTM-Conv),显著提高了燃油消耗预测和经济性估算的精度与稳定性。Xu[19]使用XGBoost分析了驾驶行为、司机特征及行程特征对CO2eq和PM2.5排放的影响,并利用SHAP方法解释了关键因素对行程排放和驾驶生态评分的贡献。Kabir[20]使用LSTM预测信号化交叉口的燃油消耗,研究了交通延迟对能源消耗的影响。Liao[21]比较了7种机器学习方法在预测柴油发动机瞬态排放特性方面的表现,并提出了一种混合预测模型。Liu[22]提出了基于发动机管理系统和即时燃油计量器数据的重型卡车燃油消耗预测模型,评估了7种预测模型的表现,AutoML模型实现了最高的预测精度。总体来看,第2类模型在预测平均燃油消耗方面具有较高的准确性。
综上,现有研究在车辆油耗影响因素与预测方面已建立了较为完善的理论方法体系,但研究多关注车辆的燃油消耗而非燃油效率。燃油消耗指的是车辆在一定距离或时间内的燃油使用量,而燃油效率则反映了车辆的能源利用水平,通常以单位燃油的行驶距离表示,燃油效率更直观地反映了车辆的能源利用效率。同时,对油耗影响因素的分析大多是独立分析,没有考虑因素间交互作用对油耗的影响。因此,本研究将基于WOA-XGBoost机器学习模型预测货车的燃油效率, 同时,采用SHAP归因分析方法解释WOA-XGBoost模型,以确定货车燃油效率的主要影响因素,并进一步探究这些因素之间的交互作用对货车燃油效率的影响。
1 数据准备 1.1 数据来源本研究使用的数据为某重型汽车企业车联网系统收集的货车行驶数据,收集数据的相关信息如表 1所示。所涉及的线路包括线路1(山阳至西安)、线路2(西安至汉中)和线路3(西安至包茂),3条线路均位于陕西省境内。共收集了534 687条数据,采样间隔为5 s,每条记录中包含车辆编号、发生时间、经度、纬度、海拔高度、车速、转速、行驶里程、燃料累积使用量等81个参数,数据样例如表 2所示。
| 编号 | 线路 | 收集时间 |
| 车辆1 | 线路1 | 2021年1月1日至30日,2021年5月2日至4日 |
| 车辆2 | 线路1 | 2020-12-26,2020-12-29 |
| 车辆3 | 线路2 | 2020-12-25,2021-01-01,2021-01-13,2021-01-15,2021-01-19 |
| 车辆4 | 线路3 | 2021-01-02,2021-01-05 |
| 编号 | 发生日期和时间 | 海拔高度/m | 车速/(km·h―1) | 转速/(rev·min―1) | 燃料累积使用量/L | 行驶里程/km |
| 车辆1 | 2021-01-10,19:42:22 | 295 | 62 | 1 160 | 100 752 | 238 182.4 |
| 车辆2 | 2020-12-26,23:41:34 | 365 | 45 | 1 040 | 214 364 | 271 671.6 |
| 车辆3 | 2021-01-15,14:45:43 | 317 | 56 | 1 300 | 104 047 | 245 392.9 |
| 车辆4 | 2021-01-02,19:52:52 | 838 | 74 | 1 460 | 110 314 | 682 496.2 |
对于本研究使用的数据,由于燃料累积使用量的分辨率为1 L,因此,燃料累积使用量的每个数值代表一个样本,总共有11 191个样本。燃油效率为某个燃料累积使用量值所收集的原始数据中最大里程与最小里程的差值,其计算公式为:
| $ \begin{gathered} F= \max \left\{f_i \mid i=1, 2, \cdots, n\right\}- \\ \min \left\{f_i \mid i=1, 2, \cdots, n\right\}, \end{gathered} $ | (1) |
式中,F为燃油效率;n为每个样本中原始数据的个数;fi为每个样本中第i个数据车辆的行驶里程。
1.2 数据处理为确保数据质量并提升后续分析的准确性,本研究对采集的车辆运行数据进行预处理, 具体包括:删除重复和无效数据、按车辆编号和发生时间重新排序、识别并处理异常值、基于燃油效率定义计算相关特征,以及对数据进行归一化处理。
(1) 删除重复数据和无效数据。在车辆怠速时,发动机运转但车辆不移动;在车辆惰行或滑行时,发动机熄火,车辆利用惯性继续行驶,车速不为0。为符合现实,本研究将车辆车速和发动机转速同时为0的情况定义为无效数据。
(2) 按照车辆编号和发生时间对数据重新排序。由于数据中包含多辆车多个时间的数据,为了方便后续处理,对数据按照车辆编号和发生时间进行重新排序。
(3) 原始数据中异常值处理。原始数据中包含很多异常值,例如,有海拔高度为11 979 m的记录。因此,需要对原始数据进行异常值处理,使用箱型图筛选异常值并对其进行线性插值处理。箱型图通过计算四分位数和应用四分位距来确定异常值的上、下限,并对异常值进行线性插值,避免其对模型的训练和预测产生过大的影响。
(4) 计算样本特征。根据每个样本中包含的原始数据计算每个样本的特征,需要计算的样本特征包括刹车次数、平均海拔、平均转速、最大速度、最小速度、平均速度、速度标准差、车辆的加速时间、减速时间、巡航时间、车辆的加速份额、减速份额和巡航份额。刹车次数Bsum的计算公式为:
| $ B_{\mathrm{sum}}=\sum\limits_{i=1}^n b_i, $ | (2) |
式中bi为每个样本中第i个数据车辆是否刹车,若bi=1,则表示刹车,若bi=0,则表示未刹车。平均海拔Aaverage的计算公式为:
| $ A_{\text {average }}=\sum\limits_{i=1}^n A_i / n, $ | (3) |
式中Ai为每个样本中第i个数据车辆所处的海拔高度。平均转速Saverage的计算公式为:
| $ S_{\text {average }}=\sum\limits_{i=1}^n S_i / n, $ | (4) |
式中Si为每个样本中第i个数据车辆的转速。最大速度vpeak,最小速度vbottom,平均速度v 和速度标准差vstd的计算公式分别为:
| $ v_{\text {peak }}=\max \left\{v_1, v_2, v_3, \cdots, v_n\right\}, $ | (5) |
| $ v_{\text {bottom }}=\min \left\{v_1, v_2, v_3, \cdots, v_n\right\}, $ | (6) |
| $ \bar{v}=\sum\limits_{i=1}^n v_i / n, $ | (7) |
| $ v_{\text {std }}=\sqrt{\sum\limits_{i=1}^n\left(v_i-\bar{v}\right)^2 / n}, $ | (8) |
式中vi为每个样本中第i个数据车辆的速度。车辆的加速时间tacc,减速时间tdec,巡航时间tcru的计算公式分别为:
| $ t_{\mathrm{acc}}=\Delta t \times \sum\limits_{i=1}^{n-1}\left[\frac{v_{i+1}-v_i}{\Delta t}>0\right], $ | (9) |
| $ t_{\mathrm{dec}}=\Delta t \times \sum\limits_{i=1}^{n-1}\left[\frac{v_{i+1}-v_i}{\Delta t}<0\right], $ | (10) |
| $ t_{\mathrm{cru}}=\Delta t \times \sum\limits_{i=1}^{n-1}\left[\frac{v_{i+1}-v_i}{\Delta t}=0\right], $ | (11) |
式中,Δt为数据的采样间隔;[·]为指示函数,满足条件时为1,否则为0。车辆的加速份额VAccs,减速份额VDecs,巡航份额VCrus的计算公式分别为:
| $ V_{\mathrm{Accs}}=t_{\mathrm{acc}} /\left(t_{\mathrm{acc}}+t_{\mathrm{dec}}+t_{\mathrm{cru}}\right), $ | (12) |
| $ V_{\mathrm{Decs}}=t_{\mathrm{dec}} /\left(t_{\mathrm{acc}}+t_{\mathrm{dec}}+t_{\mathrm{cru}}\right), $ | (13) |
| $ V_{\mathrm{Crus}}=t_{\mathrm{cru}} /\left(t_{\mathrm{acc}}+t_{\mathrm{dec}}+t_{\mathrm{cru}}\right) 。$ | (14) |
(5) 数据归一化。研究以车辆燃油效率为目标值,其余参数为特征值的多输入单输出预测。由于各特征之间具有不同的量纲单位,会影响数据分析的结果。因此将数据输入模型之前要对数据做归一化处理,公式为:
| $ x^{\prime}=\frac{x-x_{\min }}{x_{\max }-x_{\min }}, $ | (15) |
式中,x′为归一化后的特征值;x为归一化前的特征实际值;xmax为特征数据的最大值;xmin为特征数据的最小值。
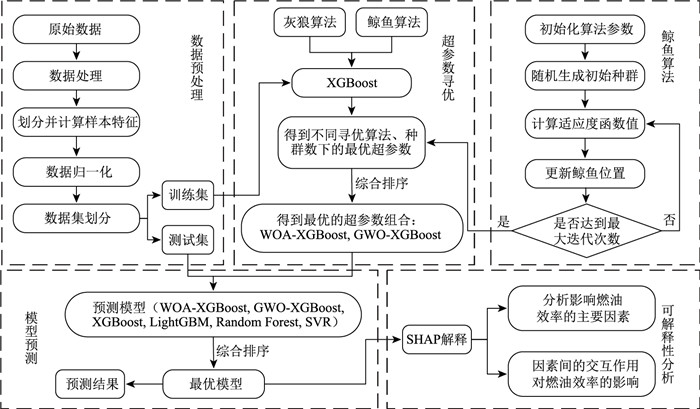
2 研究方法本研究流程如图 1所示。首先,对数据进行预处理,并将处理后的数据划分为训练集和测试集;然后分别使用鲸鱼算法(WOA)和灰狼算法(GWO)对XGBoost模型的超参数进行优化,并通过综合排序确定各算法的最优超参数;接着,与其他模型进行对比,最终选出综合表现最佳的模型,并利用SHAP方法对其进行解释。
|
| 图 1 研究流程 Fig. 1 Research workflow |
| |
2.1 优化算法
鲸鱼优化算法是由Mirjalili[23]提出的一种新型群体智能优化搜索方法,感源自自然界中座头鲸群体的狩猎行为。座头鲸通过生成气泡网来围绕猎物,并利用回声定位判断猎物的位置。基于这一行为,WOA模拟了座头鲸捕猎时不断调整自身位置的过程,以寻找最优解。该算法采用2种主要机制进行搜索:一是通过收缩包络机制逐步包围猎物;二是通过螺旋形运动模拟鲸鱼靠近猎物时的轨迹。此外,WOA还具备全局搜索能力,通过随机选择个体进行探索,进一步提高算法的搜索效率。
灰狼优化算法是由Mirjalili[24]提出的一种模拟灰狼群体捕猎行为的群体智能优化算法。该算法通过模拟灰狼的领袖层次结构、围捕、追捕和进攻猎物的过程,来寻找最优解。灰狼群体按社会地位分为α狼,β狼,δ狼,ω狼这4个等级。其中,α狼负责决策,β狼协助α狼并维护秩序,δ狼服从α狼和β狼且管理ω狼,ω狼处于最低等级并遵从其他狼的指示。在算法中,α,β,δ狼的当前位置被认为是最优解的候选者,它们会引导其他狼更新自己的位置。算法通过模拟灰狼围猎,迭代调整位置,平衡探索与开发,逐步逼近最优解。
2.2 XGBoost模型XGBoost算法由Chen[25]提出,是一种具有快速并行性、可控复杂性、容错性和强泛化能力的集成机器学习算法。XGBoost中的分类和回归树是顺序构建的,每棵新树通过纠正前一棵树的错误来提高预测准确性,最终的预测结果为所有树输出的总和。这种顺序结构减少了特征多重共线性问题。为避免过拟合,XGBoost在损失函数中引入L1/L2正则化,并采用基于损失变化的停止策略,通过并行计算特征增益和深度优先树剪枝等方法,提升训练速度和精度。XGBoost预测值的计算公式为:
| $ \hat{y}_i=\sum\limits_{k=1}^K f_k\left(\boldsymbol{x}_i\right), f_k \in \zeta, $ | (16) |
式中,
为了减少过拟合,在XGBoost的优化目标函数中加入一个正则项,其目标函数计算公式为:
| $ O=\sum\limits_{i=1}^M l\left(y_i, \hat{y}_i\right)+\sum\limits_{k=1}^K \Omega\left(f_k\right), $ | (17) |
| $ \Omega\left(f_k\right)=\gamma T+\frac{1}{2} \lambda\|\omega\|^2, $ | (18) |
式中,M为总样本数量;yi和
对于第i个样本在第t次迭代中的预测值
| $ O^t=\sum\limits_{i=1}^M l\left[\left(y_i, \hat{y}_i^{t-1}+f_t\left(\boldsymbol{x}_i\right)\right]+\Omega\left(f_t\right) 。\right. $ | (19) |
通过对损失函数进行泰勒展开的二阶近似计算,可以加快优化过程,其公式为:
| $ O^t=\sum\limits_{i=1}^M\left[g_i f_t\left(\boldsymbol{x}_i\right)+\frac{1}{2} h_i f_t^2\left(\boldsymbol{x}_i\right)\right]+\Omega\left(f_t\right), $ | (20) |
| $ g_i=\partial_{\hat{y}^{(t-1)}} l\left(y_i, \hat{y}_i^{t-1}\right), $ | (21) |
| $ h_i=\partial_{\hat{y}^{(t-1)}}^2 l\left(y_i, \hat{y}_i^{t-1}\right), $ | (22) |
式中gi和hi分别为损失函数的一阶和二阶梯度统计。
2.3 SHAP方法SHAP是由Lundberg[26]提出的一种用于解释模型输出的框架,结合了博弈论和局部解释的概念,其核心原理是基于Shapley值的概念。在解释机器学习模型的预测时,SHAP使用Shapley值来衡量每个特征对于模型输出的贡献,从而为每个测试样本生成可解释的预测。计算SHAP值的主要思想是衡量每个特征对于模型对样本预测的影响,即特征对于模型预测值的边际贡献。在合作博弈论中,SHAP值计算为:
| $ g(x)=\phi_0+\sum\limits_{j=1}^N \phi_j x_j, $ | (23) |
| $ \begin{gathered} \phi_j= \sum\limits_{S \subseteq N \backslash\{j\}} \frac{|S|!(N-|S|-1)!}{N!} . \\ {\left[f_{S \cup\{j\}}\left(x_{S \cup\{j\}}\right)-f_S\left(x_S\right)\right], } \end{gathered} $ | (24) |
式中,g (x)为样本x的解释模型预测;ϕ0为模型的预测基准值,即所有样本SHAP值的均值;xj为第j个特征的样本;ϕj为第j个特征的shapley值;N为所有特征的集合;S为N不含特征j的子集;f为模型的预测函数,其输入为特征的子集;|S|为集合S中的特征数量; S∪{j}为子集S中增加特征j的集合;fS∪{j} (xS∪ {j })与fS (xS)分别为包含特征j和不包含特征j的预测值。
3 结果分析与讨论 3.1 模型结果分析在所有试验中,使用数据集划分策略函数(train_test_split)将数据划分为训练集和测试集,比例分别为70%和30%。为了确保在不同试验中数据划分的一致性和结果的可复现性,将随机状态设定参数(random_state)设置为5。在所有试验中, 均选择均方误差(MSE)、平均绝对误差(MAE)、均方根误差(RMSE)、决定系数(R2)作为模型的评价指标。计算公式为:
| $ E_{\mathrm{MSE}}=\sum\limits_{i=1}^n\left(y_i-\hat{y}_i\right)^2 / n, $ | (25) |
| $ E_{\mathrm{MAE}}=\sum\limits_{i=1}^n\left|y_i-\hat{y}_i\right| / n, $ | (26) |
| $ E_{\mathrm{RMSE}}=\sqrt{\sum\limits_{i=1}^n\left(y_i-\hat{y}_i\right)^2 / n}, $ | (27) |
| $ R^2=1-\sum\limits_{i=1}^n\left(y_i-\bar{y}_i\right)^2 / \sum\limits_{i=1}^n\left(y_i-\bar{y}_i\right)^2, $ | (28) |
式中,E为误差;yi为真实值;
对于WOA-XGBoost和GWO-XGBoost模型,需要对WOA和GWO算法的相关参数进行设置。将WOA算法的对数螺旋形状常数b设置为1,对数螺旋因子l的范围设置为[― 1,1]。将GWO算法的衰减系数a初始值设置为2,并随着迭代逐步减小到0。将WOA和GWO算法的种群大小设置为5,10,15,…,120,共计24个试验。在不同种群大小下,对XGBoost的超参数(最大深度[3,10],学习率[0.01,0.3],树的数量[50,200])进行寻优,其他参数使用默认值。由于算法结果的不确定性,对WOA和GWO的超参数优化进行多次试验,分别选择结果较好的6组超参数进行比较。
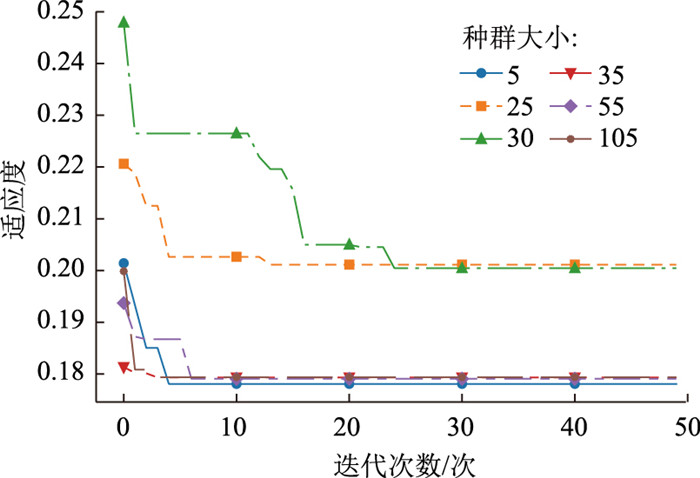
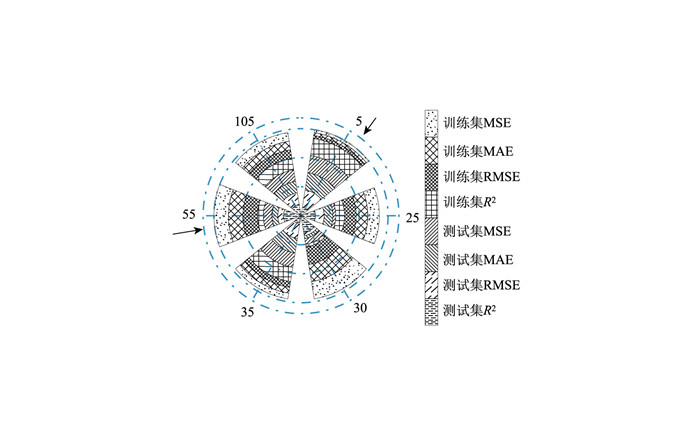
在不同种群值下,WOA-XGBoost模型在50次迭代后均达到了稳定状态,其适应值变化如图 2所示。不同种群下模型的最优超参数和结果如表 3所示。由于不同种群值下模型的评价指标各有差异,难以确定最佳超参数,因此需要综合评价不同种群值下的模型性能。综合评价结果如图 3,其中箭头指向表现最优的模型,WOA-XGBoost模型的最优种群为5或55。当种群数量为5时,模型在测试集上的MSE值为0.251 2,MAE值为0.145 7,RMSE值为0.501 2,R2为0.968 0,模型的最佳参数组合为(最大深度为6,学习率为0.196 9,树的数量为131)。
|
| 图 2 WOA-XGBoost模型在不同种群中的适应度变化曲线 Fig. 2 Fitness variation curves of WOA-XGBoost model in different populations |
| |
| 数据集 | WOA种群数量-超参数 | MSE值 | 排名 | MAE值 | 排名 | RMSE值 | 排名 | R2 | 排名 |
| 训练集 | 5-(6,0.196 9,131) | 0.005 2 | 1 | 0.053 2 | 1 | 0.072 0 | 1 | 0.999 4 | 3 |
| 25-(7,0.236 9,157) | 0.001 4 | 4 | 0.028 0 | 4 | 0.037 1 | 4 | 0.999 8 | 5 | |
| 30-(8,0.260 4,173) | 0.000 3 | 6 | 0.011 0 | 6 | 0.015 9 | 6 | 0.999 9 | 6 | |
| 35-(6,0.204 5,136) | 0.005 1 | 2 | 0.053 0 | 2 | 0.071 6 | 2 | 0.999 4 | 3 | |
| 55-(9,9.576 9,199) | 0.000 8 | 5 | 0.020 6 | 5 | 0.027 8 | 5 | 0.999 9 | 6 | |
| 105-(8,0.005 3,178) | 0.004 2 | 3 | 0.047 8 | 3 | 0.064 5 | 3 | 0.999 5 | 4 | |
| 测试集 | 5-(6,0.196 9,131) | 0.251 2 | 6 | 0.145 7 | 6 | 0.501 2 | 6 | 0.968 0 | 6 |
| 25-(7,0.236 9,157) | 0.309 0 | 3 | 0.153 3 | 1 | 0.555 9 | 3 | 0.960 7 | 3 | |
| 30-(8,0.260 4,173) | 0.334 3 | 1 | 0.150 9 | 2 | 0.578 2 | 1 | 0.957 5 | 1 | |
| 35-(6,0.204 5,136) | 0.264 9 | 5 | 0.147 0 | 5 | 0.514 7 | 5 | 0.966 3 | 5 | |
| 55-(9,9.576 9,199) | 0.310 6 | 2 | 0.149 6 | 3 | 0.557 3 | 2 | 0.960 5 | 2 | |
| 105-(8,0.005 3,178) | 0.305 2 | 4 | 0.148 6 | 4 | 0.552 5 | 4 | 0.961 2 | 4 |
|
| 图 3 WOA-XGBoost模型综合评价 Fig. 3 Comprehensive evaluation on WOA-XGBoost model |
| |
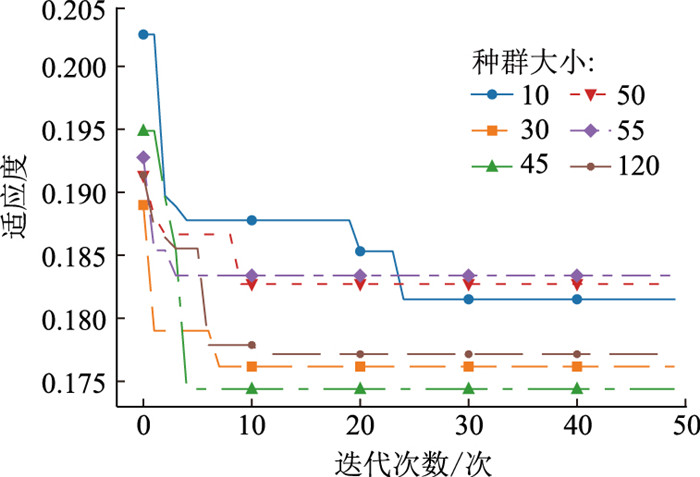
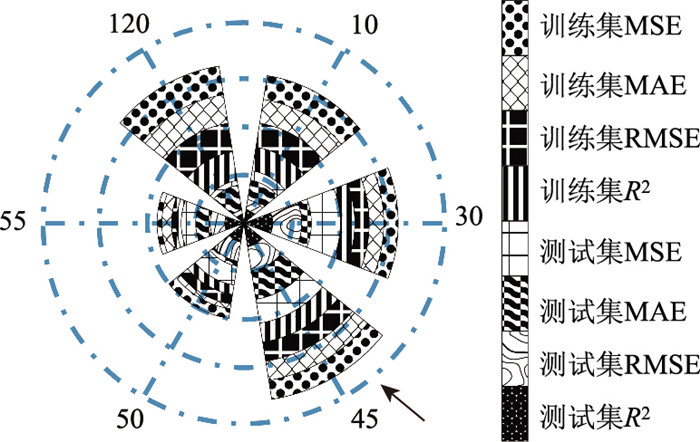
对于GWO-XGBoost模型,在不同种群值下,当迭代次数达到50次时GWO-XGBoost模型均达到了稳定状态,其适应值的变化如图 4所示,GWO-XGBoost模型在不同种群下的最优超参数和模型结果如表 4所示,GWO-XGBoost模型的综合评价结果如图 5所示。WOA-XGBoost模型的最优种群为45,其测试集上的MSE值为0.202 8,MAE值为0.146 4,RMSE值为0.450 4和R2为0.974 2。此时,XGBoost模型的最佳参数组合为(最大深度为4,学习率为0.208 8,树的数量为200)。
|
| 图 4 GWO-XGBoost模型在不同种群中适应度变化曲线 Fig. 4 Fitness variation curves of GWO-XGBoost model in different populations |
| |
| 数据集 | GWO种群数量-超参数 | MSE值 | 排名 | MAE值 | 排名 | RMSE值 | 排名 | R2 | 排名 |
| 训练集 | 10-(6,0.281 9,57) | 0.011 6 | 5 | 0.074 3 | 5 | 0.107 8 | 5 | 0.998 6 | 5 |
| 30-(3,0.300 0,172) | 0.036 2 | 3 | 0.125 1 | 3 | 0.190 4 | 3 | 0.995 6 | 3 | |
| 45-(4,0.208 8,200) | 0.016 3 | 4 | 0.086 4 | 4 | 0.127 7 | 4 | 0.998 0 | 4 | |
| 50-(3,0.300 0,131) | 0.046 2 | 2 | 0.137 5 | 1 | 0.215 0 | 2 | 0.994 4 | 2 | |
| 55-(4,0.175 1,62) | 0.051 6 | 1 | 0.132 8 | 2 | 0.227 2 | 1 | 0.993 7 | 1 | |
| 120-(8,0.137 6,91) | 0.003 2 | 6 | 0.042 2 | 6 | 0.056 2 | 6 | 0.999 6 | 6 | |
| 测试集 | 10-(6,0.281 9,57) | 0.274 6 | 2 | 0.155 2 | 4 | 0.524 0 | 2 | 0.965 1 | 3 |
| 30-(3,0.300 0,172) | 0.197 4 | 6 | 0.177 1 | 2 | 0.444 3 | 6 | 0.974 9 | 6 | |
| 45-(4,0.208 8,200) | 0.202 8 | 5 | 0.146 4 | 6 | 0.450 4 | 5 | 0.974 2 | 5 | |
| 50-(3,0.300 0,131) | 0.205 0 | 4 | 0.183 0 | 1 | 0.452 8 | 4 | 0.973 9 | 4 | |
| 55-(4,0.175 1,62) | 0.205 5 | 3 | 0.168 3 | 3 | 0.453 4 | 3 | 0.973 9 | 4 | |
| 120-(8,0.137 6,91) | 0.312 8 | 1 | 0.150 2 | 5 | 0.559 3 | 1 | 0.960 2 | 2 |
|
| 图 5 GWO-XGBoost模型综合评价 Fig. 5 Comprehensive evaluation on GWO-XGBoost model |
| |
本研究还考虑了XGBoost,LightGBM,Random Forest,SVR模型,比较了货车真实记录的燃油效率与6种模型预测的燃油效率,如图 6所示。图中对角线代表真实的燃油效率,圆形和三角形的散点图分别代表训练集和测试集的预测值,对角线上下的2条虚线则分别表示预测值相对于真实值的±10%偏差范围。

|
| 图 6 6种模型对燃油效率的预测结果 Fig. 6 Fuel efficiency prediction results with 6 models |
| |
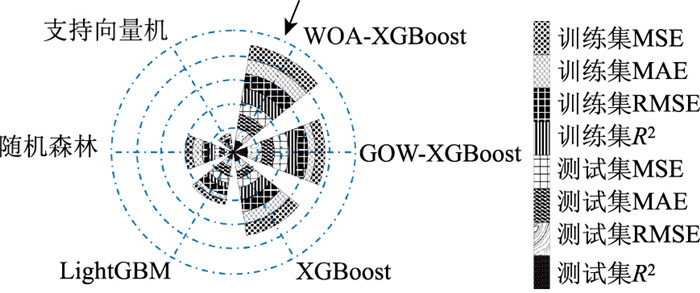
所有预测模型的性能结果及其综合排名如表 5和图 7所示。由表 5可见,在训练集上WOA-XGBoost模型对燃油效率的预测性能最好,在测试集上GWO-XGBoost模型对燃油效率的预测性能最好。由图 7可知,WOA-XGBoost模型整体预测性能最好。具体而言,在测试集上,该模型的MSE,MAE,RMSE,R2分别达到了0.251 2,0.145 7,0.501 2,0.968 0。相较于传统的XGBoost模型,WOA-XGBoost模型在测试集上的表现有了显著提升,MSE,MAE,RMSE的值分别减少了0.068 3,0.010 4,0.064 0;R2的值增加了0.86%。这表明WOA-XGBoost模型在燃油效率预测中的精度得到了显著提高。
| 数据集 | 模型 | MSE值 | 排名 | MAE值 | 排名 | RMSE值 | 排名 | R2 | 排名 |
| 训练集 | WOA-XGBoost | 0.005 2 | 6 | 0.053 2 | 6 | 0.072 0 | 6 | 0.999 4 | 6 |
| GWO-XGBoost | 0.016 3 | 4 | 0.086 4 | 3 | 0.127 7 | 4 | 0.998 0 | 4 | |
| XGBoost | 0.005 6 | 5 | 0.054 2 | 5 | 0.074 5 | 5 | 0.999 3 | 5 | |
| LightGBM | 0.044 4 | 2 | 0.098 2 | 2 | 0.210 7 | 3 | 0.994 6 | 2 | |
| 随机森林 | 0.028 3 | 3 | 0.058 7 | 4 | 0.168 2 | 2 | 0.996 5 | 3 | |
| 支持向量机 | 1.266 6 | 1 | 0.470 4 | 1 | 1.125 4 | 1 | 0.845 4 | 1 | |
| 测试集 | WOA-XGBoost | 0.251 2 | 5 | 0.145 7 | 6 | 0.501 2 | 5 | 0.968 0 | 5 |
| GWO-XGBoost | 0.202 8 | 6 | 0.146 4 | 5 | 0.450 4 | 6 | 0.974 2 | 6 | |
| XGBoost | 0.319 5 | 4 | 0.156 1 | 3 | 0.565 2 | 4 | 0.959 4 | 4 | |
| LightGBM | 0.362 0 | 3 | 0.153 0 | 4 | 0.601 7 | 3 | 0.954 0 | 3 | |
| 随机森林 | 0.417 4 | 2 | 0.160 2 | 2 | 0.646 0 | 2 | 0.946 9 | 2 | |
| 支持向量机 | 1.633 9 | 1 | 0.457 5 | 1 | 1.278 2 | 1 | 0.792 2 | 1 |
|
| 图 7 各模型综合排名 Fig. 7 Overall rankings of various models |
| |
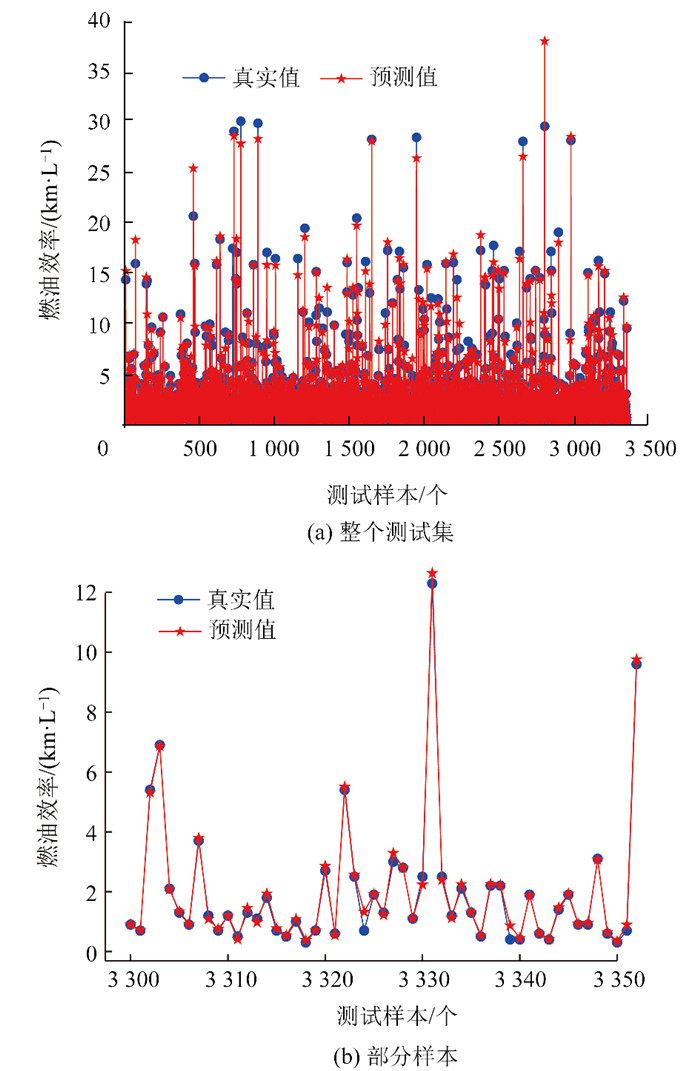
WOA-XGBoost模型的预测结果如图 8所示,可以更清楚地看到预测值与真实值之间的差异。因此,选择WOA-XGBoost模型作为SHAP的可解释模型。
|
| 图 8 WOA-XGBoost预测结果 Fig. 8 Prediction result with WOA-XGBoost |
| |
3.2 基于SHAP归因分析的可视化解释 3.2.1 主要影响因素分析
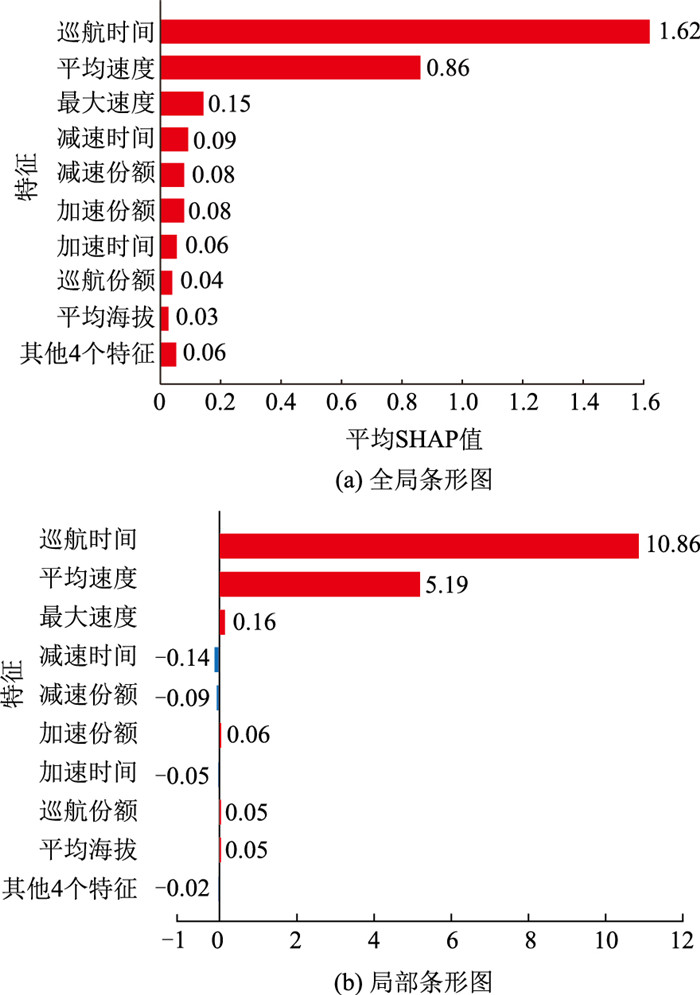
使用SHAP解释W OA-XGBoost模型,结果如 图 9所示。图 9(a)中的全局条形图展示了WOA-XGBoost模型中各特征对燃油效率预测的影响。其中,巡航时间对预测结果的影响最大,其次是平均速度,之后的特征对模型输出的影响都较小,其他4个特征是指速度标准差、最小速度、平均转速和刹车次数。图 9(b)是针对单个样本创建的局部条形图,在该样本中,SHAP值大于0表示对模型具有正向影响,反之则有负向影响。
|
| 图 9 特征重要性排序 Fig. 9 Feature importance ranking |
| |
使用13个特征训练的WOA-XGBoost模型的SHAP摘要图如图 10所示。根据特征对燃油效率预测的影响进行排名。每个点代表一个样本的SHAP值,正值表明正向影响,负值表明负向影响。巡航时间对模型预测影响最大,其次是平均速度,且随着这2个特征数值的增加,SHAP值呈正向增长趋势,对燃油效率产生更大的正面影响。

|
| 图 10 SHAP摘要图 Fig. 10 SHAP summary graph |
| |
通过分析特征重要性排序图和SHAP摘要图,发现巡航时间和平均速度对燃油效率的影响最大。从整体来看,巡航时间和平均速度越大,对燃油效率的正向影响越显著,货车的燃油效率也越高。这一现象可以通过车辆的运行状态来解释:较长的巡航时间意味着车辆处于匀速行驶状态,发动机负荷稳定,减少了频繁加速和减速带来的额外油耗。同时,较高的平均速度通常表明车辆运行在高速公路等路况较好的环境下,此时空气阻力相对较小,传动系统效率更高,进一步提升了燃油效率。
3.2.2 因素的交互影响分析为进一步分析各因素间的交互效应,选取巡航时间、平均速度和最大速度这3个影响较大的因素作为主特征,并根据特征间的交互作用程度计算其他影响因素的边际贡献,筛选出交互作用最强的因素作为次要特征。以横坐标为主特征值,纵坐标为SHAP值绘制散点图,次要特征大小表现为散点的颜色,如图 11所示。

|
| 图 11 不同因素的交互作用 Fig. 11 Interactions among various factors |
| |
分析主特征值与SHAP值的关系,发现其SHAP值均随主特征值的增加而增加。平均速度与巡航时间互为交互作用最大的特征,最大速度交互作用最大的特征是最小速度。对给定的巡航时间,平均速度的增加会加大巡航时间对模型输出的影响。对给定的平均速度,随着巡航时间的增加,平均速度对模型输出的影响也随之增加。
巡航时间对燃油效率有显著影响,这主要是由于车辆在长时间巡航时,发动机的负荷和转速保持相对稳定,避免了频繁的加速、减速过程。当平均速度约为40 km/h时,该变量的SHAP值由负变正。这种变化可能与低速行驶时发动机低负荷运行、燃烧效率较低及频繁启停等有关。而当货车以较高速度行驶时,接近经济速度,发动机运行更高效,减少加速和减速降低能量损失,并与最佳变速器匹配,减少换挡损失,提高燃油效率。当最大速度为65 km/h时,最大速度对燃油效率的影响由负变正。交互分析结果表明,驾驶员在驾驶过程中通过控制不同特征大小组合可进一步提升燃油效率。
4 结论本研究以货车的油耗数据为基础,构建了基于WOA-XGBoost和SHAP的可解释货车燃油效率预测模型,对货车的燃油效率进行预测并解释其主要影响因素和因素间的交互作用。
(1) 使用WOA和GWO算法在不同种群下对XGBoost进行寻优,WOA-XGBoost和GWO-XGBoost模型的最优种群(最佳参数)分别为5(6,0.196 9,131)和45(4,0.208 8,200)。将其与XGBoost,LightGBM,随机森林和支持向量机模型进行比较,综合排名最高的WOA-XGBoost模型具有良好的预测性能。
(2) 使用全局条形图和SHAP摘要图分析了XGBoost模型中各特征对模型输出的影响及SHAP值分布,其中巡航时间对模型输出的影响最大,其次是平均速度和最大速度等特征,巡航时间、平均速度和最大速度的平均SHAP值分别为1.62,0.86,0.15。
(3) 巡航时间和平均速度互为交互作用最大的特征。巡航时间的SHAP值随着巡航时间的增加而增加。此外,对给定的巡航时间,平均速度的增加会加大巡航时间对模型输出的影响。对平均速度进行交互分析后发现,当平均速度约为40 km/h时,其SHAP值由负变为正。对给定的平均速度,随着巡航时间的增加,平均速度对模型输出的影响也随之增加。具体表现为速度大于40 km/h时的正向影响增加,速度小于40 km/h时的负向影响增加。
(4) 当最大速度为65 km/h时,最大速度对燃油效率的影响由负变正。当最大速度小于65 km/h时,最大速度的SHAP值稳定在-0.25~0之间,没有明显的变化;当最大速度大于65 km/h时,随着最大速度的增加,其对模型输出的正向影响也随之增加。
本研究提出的方法虽然对燃油效率具有较好的预测性能,但是由于数据的限制,无法分析不同驾驶风格的驾驶员对燃油效率的影响。下一步研究中,可结合更多外部因素,如道路条件和环境变量,以进一步提升模型的泛化能力与适用性。
| [1] |
李宁海, 陈硕, 梁肖, 等. 我国交通运输业碳达峰时间预测[J]. 交通运输系统工程与信息, 2024, 24(1): 2-13, 54. LI Ninghai, CHEN Shuo, LIANG Xiao, et al. Prediction of transportation industry carbon peak in China[J]. Transportation Systems Engineering and Information Technology, 2024, 24(1): 2-13, 54. |
| [2] |
常征, 宋艳, 姬美臣, 等. 运营车辆碳排放监测和管理体系构建[J]. 中外公路, 2024, 44(4): 255-262. CHANG Zheng, SONG Yan, JI Meichen, et al. Construction of carbon emission monitoring and management system for commercial vehicles[J]. Journal of China & Foreign Highway, 2024, 44(4): 255-262. |
| [3] |
LI X Y, TAN X Y, WU R, et al. Paths for carbon peak and carbon neutrality in transport sector in China[J].
Strategic Study of Chinese Academy of Engineering, 2021, 23(6): 15-21.
|
| [4] |
ZHOU M, JIN H, WANG W X. A review of vehicle fuel consumption models to evaluate eco-driving and eco-routing[J].
Transportation Research Part D: Transport and Environment, 2016, 49: 203-218.
|
| [5] |
DÍAZ-RAMIREZ J, GIRALDO-PERALTA N, FLÓREZ-CERON D, et al. Eco-driving key factors that influence fuel consumption in heavy-truck fleets: A Colombian case[J].
Transportation Research Part D: Transport and Environment, 2017, 56: 258-270.
|
| [6] |
YAO Y, ZHAO X H, LIU C, et al. Vehicle fuel consumption prediction method based on driving behavior data collected from smartphones[J/OL]. Journal of Advanced Transportation, 2020. (2020-03-23)[2024-11-01]. https://doi.org/10.1155/2020/9263605.
|
| [7] |
程颖, 张佳乐, 张少君, 等. 大型货运车辆生态驾驶及节油潜力评估[J]. 交通运输系统工程与信息, 2020, 20(6): 253-258. CHENG Ying, ZHANG Jiale, ZHANG Shaojun, et al. Evaluation of eco-driving behavior and fuel-saving potential of large freight vehicles[J]. Transportation Systems Engineering and Information Technology, 2020, 20(6): 253-258. |
| [8] |
马荣影, 韩锐, 艾曦锋, 等. 基于Python的汽车油耗多参数回归模型构建方法[J]. 公路交通科技, 2020, 37(6): 145-150. MA Rongying, HAN Rui, AI Xifeng, et al. A method for constructing multi-parameter regression model of vehicle fuel consumption based on Python[J]. Journal of Highway and Transportation Research and Development, 2020, 37(6): 145-150. DOI:10.3969/j.issn.1002-0268.2020.06.018 |
| [9] |
FAN P F, YIN H, LU H Y, et al. Which factor contributes more to the fuel consumption gap between in-laboratory vs. real-world driving conditions? An independent component analysis[J/OL]. Energy Policy, 2023, 182: 113739. https://doi.org/10.1016/j.enpol.2023.113739.
|
| [10] |
HE L Q, YOU Y, ZHENG X, et al. The impacts from cold start and road grade on real-world emissions and fuel consumption of gasoline, diesel and hybrid-electric light-duty passenger vehicles[J/OL]. Science of The Total Environment, 2022, 851: 158045. (2022-12-10)[2024-11-01]. https://doi.org/10.1016/j.scitotenv.2022.158045.
|
| [11] |
姜壁刚, 何超, 王艳艳, 等. 道路坡度对轻型柴油车二氧化碳排放的影响[J]. 公路交通科技, 2025, 42(2): 207-214. JIANG Bigang, HE Chao, WANG Yanyan, et al. Influence of road gradient on CO2 emission from light-duty diesel vehicles[J]. Journal of Highway and Transportation Research and Development, 2025, 42(2): 207-214. DOI:10.3969/j.issn.1002-0268.2025.02.022 |
| [12] |
GONG J, SHANG J Z, LI L, et al. A comparative study on fuel consumption prediction methods of heavy-duty diesel trucks considering 21 influencing factors[J/OL]. Energies, 2021, 14(23): 8106. (2021-12-03) [2024-11-01]. https://doi.org/10.3390/en14238106.
|
| [13] |
ZHAO D F, LI H Y, HOU J J, et al. A review of the data-driven prediction method of vehicle fuel consumption[J/OL]. Energies, 2023, 16(14): 5258. (2023-07-09)[2024-11-01]. https://doi.org/10.3390/en16145258.
|
| [14] |
WANG J H, RAKHA H A. Fuel consumption model for heavy duty diesel trucks: Model development and testing[J].
Transportation Research Part D: Transport and Environment, 2017, 55: 127-141.
|
| [15] |
PENG C, WANG Y Y, XU T, et al. Transient fuel consumption prediction for heavy-duty trucks using on-road measurements[J].
International Journal of Sustainable Transportation, 2023, 17(8): 956-967.
|
| [16] |
HUANG W K, GUO Y Y, XU X X. Evaluation of real-time vehicle energy consumption and related emissions in China: A case study of the Guangdong-Hong Kong-Macao Greater Bay Area[J/OL]. Journal of Cleaner Production, 2020, 263: 121583. (2020-08-01)[2024-11-01]. https://doi.org/10.1016/j.jclepro.2020.121583.
|
| [17] |
师国东, 胡明茂, 宫爱红, 等. 基于XGBoost-MSIWOA-LSTM的车辆油耗优化预测模型[J/OL]. 计算机集成制造系统(2023-07-25)[2024-11-01]. https://kns.cnki.net/kcms/detail/11.5946.TP.20230724.1508.002.html. SHI Guodong, HU Mingmao, GONG Aihong, et al. The vehicle fuel consumption optimization prediction model based on XGBoost-MSIWOA-LSTM[J/OL]. Computer Integrated Manufacturing Systems(2023-07-25)[2024-11-01]. https://kns.cnki.net/kcms/detail/11.5946.TP.20230724.1508.002.html. |
| [18] |
FAN P F, SONG G H, ZHAI Z Q, et al. Fuel consumption estimation in heavy-duty trucks: Integrating vehicle weight into deep-learning frameworks[J/OL]. Transportation Research Part D: Transport and Environment, 2024, 130: 104157. https://doi.org/10.1016/j.trd.2024.104157.
|
| [19] |
XU J S, SALEH M, HATZOPOULOU M. A machine learning approach capturing the effects of driving behaviour and driver characteristics on trip-level emissions[J/OL]. Atmospheric Environment, 2020, 224: 117311. (2020-03-01)[2024-11-01]. https://doi.org/10.1016/j.atmosenv.2020.117311.
|
| [20] |
KABIR R, REMIAS S M, WADDELL J, et al. Time-series fuel consumption prediction assessing delay impacts on energy using vehicular trajectory[J/OL]. Transportation Research Part D: Transport and Environment, 2023, 117: 103678. https://doi.org/10.1016/j.trd.2023.103678.
|
| [21] |
LIAO J X, HU J, YAN F W, et al. A comparative investigation of advanced machine learning methods for predicting transient emission characteristic of diesel engine[J/OL]. Fuel, 2023, 350: 128767. (2023-10-15)[2024-11-01]. https://doi.org/10.1016/j.fuel.2023.128767.
|
| [22] |
LIU L K, LI W, WANG D W, et al. Fuel rate prediction for heavy-duty trucks[J].
IEEE Transactions on Intelligent Transportation Systems, 2023, 24(8): 8222-8235.
|
| [23] |
MIRJALILI S, LEWIS A. The whale optimization algorithm[J].
Advances in Engineering Software, 2016, 95: 51-67.
|
| [24] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J].
Advances in Engineering Software, 2014, 69: 46-61.
|
| [25] |
CHEN T Q, GUESTRIN C. XGBoost: A scalable tree boosting system[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: Association for Computing Machinery, 2016: 785-794.
|
| [26] |
LUNDBERG S M, LEE S I. A unified approach to interpreting model predictions[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. New York: Curran Associates Inc., 2017: 4768-4777.
|
 2025, Vol. 42
2025, Vol. 42



 ,
,