扩展功能
文章信息
- 张航, 王星月, 吕能超.
- ZHANG Hang, WANG Xingyue, Lü Nengchao
- 基于CRITIC组合赋权-正态云的山岭特长隧道洞口边坡失稳风险评价
- Super-long mountain tunnel entrance slope stability risk assessment based on CRITIC combined weighting-normal cloud model
- 公路交通科技, 2025, 42(7): 170-182
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(7): 170-182
- 10.3969/j.issn.1002-0268.2025.07.018
-
文章历史
- 收稿日期: 2023-04-21
2. 武汉理工大学 智能交通系统研究中心, 湖北 武汉 430063
2. Intelligent Transportation Systems Research Center, Wuhan University of Technology, Wuhan, Hubei 430063, China
随着中国隧道工程的快速发展,山岭地区深埋、特长隧道工程日益增多,但因山岭地区存在地形多变、地貌复杂等特征,隧道洞口段施工阶段边坡失稳时有发生[1]。交通运输部于2011年颁布《公路桥梁和隧道工程施工安全风险评估指南》(以下简称“《指南》”),以指导和规范隧道施工过程中的风险评估工作。《指南》中提供了相关评估指标与评估方法,如专家调查法、模糊综合分析法等,此类方法虽易于操作,但存在精度较低的问题[2]。隧道洞口边坡失稳成因复杂,影响因素众多,许多定性指标难以进行定量化,评判标准值难以确定,使得洞口边坡失稳风险评价问题具有模糊性和随机性。因此,为提高评价结果的准确性与科学性,构建科学合理的边坡失稳风险评价模型尤显重要。
近年来众多学者对风险评价模型开展了深入研究。常规评价方法主要有灰色关联分析法[3]、集对分析法[4]、BP神经网络[5]及模糊层次分析法[6](Fuzzy Analytic Hierarchy Process,FAHP)等。在指标赋权方面,刘秀[7]采用较为客观的熵权法计算评价指标权重,结合物元可拓模型以关联度表征指标与路堑边坡风险等级的关系。冯忠居[8]选择5项评价指标,将熵权-灰关联模型应用到岩质边坡开挖风险评价中。Yang[9]提出了一种改进集对分析法的边坡失稳风险评价方法,通过AHP和熵权法分别对指标进行赋权,使用加权平均进行组合赋权,结合集对分析理论对边坡失稳风险进行评价。李国良[10]将改进的G1法与反熵权法结合,对交通基础设施发展水平进行评价。CRITIC(Criteria Importance Though Intercrieria Correlation)赋权法由Diakoulaki[11]于1995年提出,相比熵权法,CRITIC法通过标准差和相关系数更好地体现了指标间的冲突性和对比强度。在隶属度确定方面,现有方法主要根据主观取值或利用函数及经验公式进行计算,存在准确度欠佳的问题。云模型是由中国李德毅院士[12]提出的一种基于随机概率和模糊理论,利用多种隶属函数将定性表达转化为定量数值的数学模型,较好地兼顾了数据的模糊性与随机性,提高了隶属度的准确性,目前在各领域得到广泛应用[13]。Wang[14]提出了3种形式的云模型,得出一维及二维云模型在隧道施工风险评价中结果较合理。与数值计算相比,云模型计算更为简便可靠。Lin[15]把正态云模型运用到隧道施工风险评估中,使用正向云发生器计算模糊隶属矩阵,生成了隶属度雷达图。Peng[16]针对隧道突涌水风险评价问题提出归一化AHP-云模型,但选取评价指标较少,指标权重客观性不足。赵岩[17]选取5项物理学参数构成黄土隧道失稳风险评价体系,结合主成分分析法和云模型对隧道失稳风险进行评价。
从以上研究分析可知,现有隧道风险评价模型主要存在评价指标选取科学性欠佳,赋权方法单一,指标权重主观性较强,无法体现评估系统的模糊性与不确定性等问题。基于此,本研究提出CRITIC组合赋权-正态云模型,并结合《指南》中的风险划分等级,对隧道洞口边坡失稳风险进行评价,如表 1所示。以云南省某山岭特长隧道为例,对影响因素进行敏感性分析,参考专家对影响因素的认可度筛选出评价指标,从定性、定量的角度完善评价指标体系;采用组合赋权克服指标权值的主观性;利用云模型将定性指标定量化,使用正向云发生器提高指标隶属度的准确性,进一步提升评价结果的科学性。
| 评价等级 | 评价结果范围 | 说明 |
| Ⅰ | [1,1.5] | 安全,发生的可能性基本可忽略。 |
| Ⅱ | [1.5,2.5] | 比较安全,但需引起重视。 |
| Ⅲ | [2.5,3.5] | 不安全,发生的可能性较大,需要采取一定的控制措施。 |
| Ⅳ | [3.5,4] | 极不安全,很有可能发生洞口失稳事故,必须采取控制措施并制定相应的应急预案。 |
1 评价指标体系建立 1.1 影响因素敏感性分析
根据查阅边坡失稳事故资料及相关文献[18-20],结合《指南》中隧道风险事件及风险源检查表,对洞口边坡失稳风险事件的风险源进行检查和确认,从地形地貌、地质条件、气候水文和施工因素4个维度出发,初步筛选出27项影响因素。使用德尔菲法邀请从事公路隧道设计与施工领域的9位企业高工和9位高校教授从“系统性”、“科学性”、“易测性”和“简明性”4个角度对以上27项影响因素的合理性进行打分。设第p位专家对第q项指标的认可度为Hq,认可度打分值最高为4分,最低为0分,即Hq∈ [0, 4]。各指标专家认可度的平均值记为Hp,Hp计算公式[21]见式(1)。
| $ H_p=\frac{1}{18} \sum\limits_{p=1}^{18} H_q \text { 。} $ | (1) |
本研究引入经济学中“敏感性”概念,以隧道洞口边坡失稳风险为目标函数,将不确定性影响因素中对目标函数影响程度较大的指标称为敏感性指标因素。式(1)计算结果即反映影响因素的敏感性程度,取Hp作为指标的敏感性分布值,专家对指标认可度的打分值及指标敏感性分布值见图 1。

|
| 图 1 影响因素筛选 Fig. 1 Influencing factors selection |
| |
1.2 评价指标筛选
对照图 1,参照文献[21]中认可程度分级值,选择敏感性分布值大于等于3的因素作为评价指标,形成了以洞口边坡失稳为评价总目标,以地形地貌、地质条件、气候水文和施工因素为一级指标,以坡高、坡度等19项因素为二级指标的洞口边坡失稳风险递阶评价指标体系,见图 2。
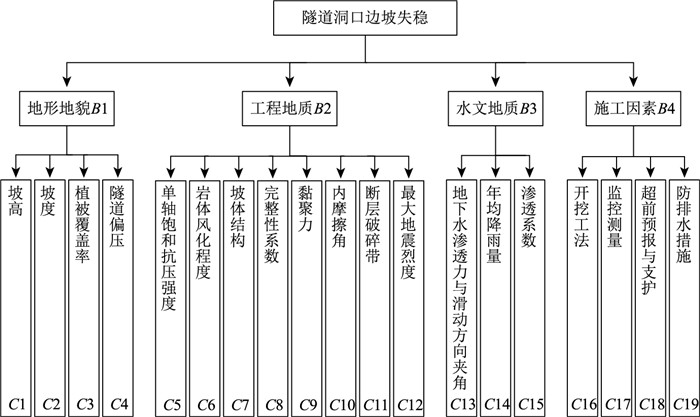
|
| 图 2 山岭特长隧道洞口边坡失稳风险评价指标体系 Fig. 2 Evaluation indicator system for super-long mountain tunnel entrance slope stability risk |
| |
2 CRITIC组合赋权-正态云模型 2.1 组合赋权 2.1.1 AHP法主观权值确定
AHP是20世纪70年代美国运筹学家Saaty[22]提出的一种简洁实用的决策方法,该方法通过建立多层次递阶结构模型将复杂问题简化,常用于多指标评价。德尔菲法[23]是一种基于反馈函询形式的主观判断指标方法,常用于多目标评价问题。由德尔菲法获取专家原始评价数据后主观权重值的计算步骤如下。
(1) 初始判断矩阵的确定
初始判断矩阵中的元素为专家对评价指标进行两两比较后的打分数据,专家进行指标相对重要性打分时,使用心理学1-9度分级标度法,分级标度法具体标准见表 2。
| 判断尺度 | 定义 |
| 1 | 两要素相比,具有同样的重要性。 |
| 3 | 两要素相比,一个要素比另一个要素稍微重要。 |
| 5 | 两要素相比,一个要素比另一个要素明显重要。 |
| 7 | 两要素相比,一个要素比另一个要素强烈重要。 |
| 9 | 两要素相比,一个要素比另一个要素极端重要。 |
| 2,4,6,8 | 介于上述两相邻判断尺度之间。 |
则初始判断矩阵Ai为:
| $ \boldsymbol{A}_i=\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \vdots & \vdots & a_{i j} & \vdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right], i, j=1, 2, \cdots, n, $ | (2) |
式中aij为各指标两两比较的结果。
(2) 层次单排序及一致性检验
获取初始比较判断矩阵后,即可计算各因素对于准则层的权重值,进行层次单排序。使用特征根法[24]计算判断矩阵的特征向量,见式(3)
| $ \begin{gathered} \bar{w}_i=\frac{\sqrt[n]{\prod\limits_{j=1}^n a_{i j}}}{\sum\limits_{i=1}^n \sqrt[n]{\prod\limits_{j=1}^n a_{i j}}}, \\ \lambda_{\max }=\sum\limits_{i=1}^n \frac{(A \bar{W})_i}{n \bar{w}_i}=\frac{1}{n} \sum\limits_{i=1}^n \frac{(A \bar{W})_i}{\bar{w}_i}, \end{gathered} $ | (3) |
式中,wi为层次单排序权重值;n为初始判断矩阵的阶数;λmax为初始判断矩阵的最大特征根;W=(w1 w2 … wi)T为层次单排序权重集,记为W(1)。
为防止专家进行比较判断打分时出现严重不一致的情况,故需对各原始判矩阵进行一致性检验[25],见式(4)。
| $ \begin{gathered} I_{\mathrm{c}}=\frac{\lambda_{\max }-n}{n-1}, \\ R_{\mathrm{c}}=\frac{I_{\mathrm{c}}}{R I}, \end{gathered} $ | (4) |
式中,Ic为一致性指标;Rc为随机一致性比率;RI为平均随机一致性指标,通过查RI值表可知。若Rc越大,表明判断矩阵一致性越差;若Rc < 0.1,表明判断矩阵满足一致性要求,计算所得权重值有效,否则需调整原始判断矩阵,对指标间重要程度重新赋值,直至原始比较判断矩阵一致性检验通过。
2.1.2 CRITIC法客观权值确定针对专家原始评分数据量纲不统一的问题,首先对式(2)进行归一化处理[26],使数据无量纲化。本研究中将评价指标划分为越大越优型正向指标和越小越优型负向指标,归一化计算公式见式(5)。
| $ a_{i j}^{\prime}=\left\{\begin{array}{c} \frac{a_{i j}-\min \left(a_{i j}\right)}{\max _j\left(a_{i j}\right)-\min \left(a_{i j}\right)}\left(a_{i j} \text { 为正向指标 }\right) \\ \frac{\max _j\left(a_{i j}\right)-a_{i j}}{\max _j\left(a_{i j}\right)-\min \left(a_{i j}\right)}\left(a_{i j} \text { 为负向指标 }\right) \end{array}, \right. $ | (5) |
式中a′ij为归一化后的判断矩阵元素。
归一化处理完毕后,计算指标的客观权值w′i,见式(6)。
| $ \begin{gathered} \sigma_j=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(a_{i j}^{\prime}-\bar{a}_{i j}^{\prime}\right)^2}, \\ y_j=\sum\limits_{t=1}^m\left(1-\frac{\operatorname{cov}(j, t)}{\sigma_j \sigma_t}\right), \\ C_j=\sigma_j y_j, \\ w_i^{\prime}=\frac{C_j}{\sum\limits_{j=1}^n C_j}, \end{gathered} $ | (6) |
式中,a′ij为归一化后的判断矩阵均值;σj为指标的标准差;cov(j,t)为指标j和指标i的协方差;yj为指标间冲突性;Cj为第j项指标包含的信息。计算得到客观权重集,记为W(2)= (w′1 w′2 … w′i)T。
2.1.3 博弈论组合权值确定基于博弈论[27]的组合赋权能够在不同的权重中找到均衡,使组合权重和各权重的偏差最小化。首先将权值进行任意线性结合,对组合系数进行求解,求解优化组合系数αj的目标函数见式(7)。
| $ \min \left\|\sum\limits_{j=1}^2 \alpha_j \boldsymbol{W}^{(j) \mathrm{T}}-\boldsymbol{W}^{(j)}\right\|_2 。$ | (7) |
本模型中权值为主观和客观两类,故j=1,2。对式(7)求一次导数,将主观权重集W(1)和客观权重集W(2)代入得线性方程组
| $ \left[\begin{array}{ll} \boldsymbol{W}^{(1)} \boldsymbol{W}^{(1) \mathrm{T}} & \boldsymbol{W}^{(1)} \boldsymbol{W}^{(2) \mathrm{T}} \\ \boldsymbol{W}^{(2)} \boldsymbol{W}^{(1) \mathrm{T}} & \boldsymbol{W}^{(2)} \boldsymbol{W}^{(2) \mathrm{T}} \end{array}\right]\left[\begin{array}{l} \alpha_1 \\ \alpha_2 \end{array}\right]=\left[\begin{array}{l} \boldsymbol{W}^{(1)} \boldsymbol{W}^{(1) \mathrm{T}} \\ \boldsymbol{W}^{(2)} \boldsymbol{W}^{(2) \mathrm{T}} \end{array}\right] 。$ | (8) |
根据式(8)解得最优组合系数α1, α2,再将系数归一化处理后得到组合权重集。
| $ \boldsymbol{W}=\alpha_1^{\prime} \boldsymbol{W}^{(1)}+\alpha_2^{\prime} \boldsymbol{W}^{(2)}, $ | (9) |
式中,
云模型以云发生器生成云图的形式通过指标的数值特征完成定性向定量的转变。云模型的定义为设一定量论域X={xi},D为X上的定性概念。对于X中的任意元素xi,均存在一个趋于稳定的随机数μi∈ [0, 1]称为xi对D的隶属度。若存在xi∈D,则xi在X中的分布即为云模型,(xi,μi)为组成云模型的云滴坐标。
2.2.1 云模型数值特征确定三项基本数值特征Ex,En及He是构建云模型的基础,可共同表征评价体系中的定性指标,标记为C (Ex,En,He),其具体含义见表 3。
| 符号 | 名称 | 含义 |
| Ex | 期望 | 反应定性概念的论域中心值 |
| En | 熵 | 定性概念可被度量的范围 |
| He | 超熵 | 熵值的不确定性与模糊性 |
Ex=0,En=1,He=0.1,需要生成的云滴数N=3 000的一维正态云图见图 3。
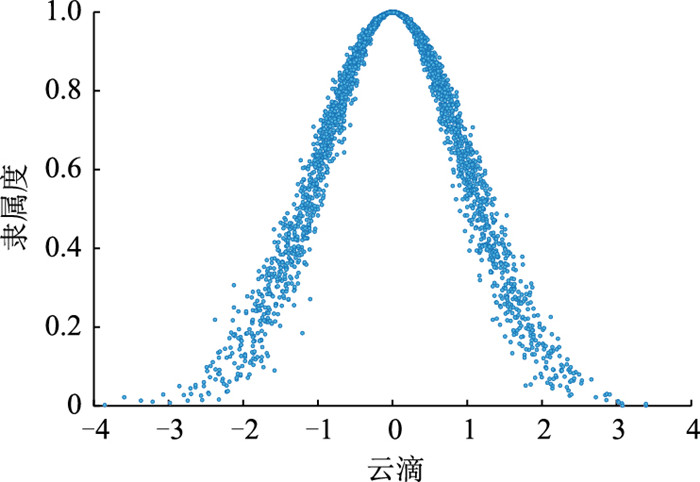
|
| 图 3 一维正态云图 Fig. 3 One-dimensional normal cloud image |
| |
参照表 1,通过指标对应风险等级的基准界限值计算得到C (Ex,En,He)称为标准云,计算公式见式(10)。
| $ \left\{\begin{array}{l} E_{\mathrm{x}}=\frac{l_{\max }+l_{\min }}{2} \\ E_{\mathrm{n}}=\frac{l_{\max }-l_{\min }}{2.355} \\ H_{\mathrm{e}}=\frac{E_n}{10} \end{array}\right. , $ | (10) |
式中lmax,lmin分别为表 1中评价指标不同风险等级对应的最大、最小界限值。
2.2.2 标准云图构建及隶属矩阵确定Ex,En及He这3项标云数值特征值确定后即可通过云发生器生成标准云图。云发生器分为正向和逆向两种。正向云发生器是从定性到定量的映射,根据输入的3个数字特征Ex,En,He及N,即可输出云滴在论域中的坐标生成云图。逆向云发生器是从定量到定性的映射,其构建步骤为正向云的逆过程,见图 4。
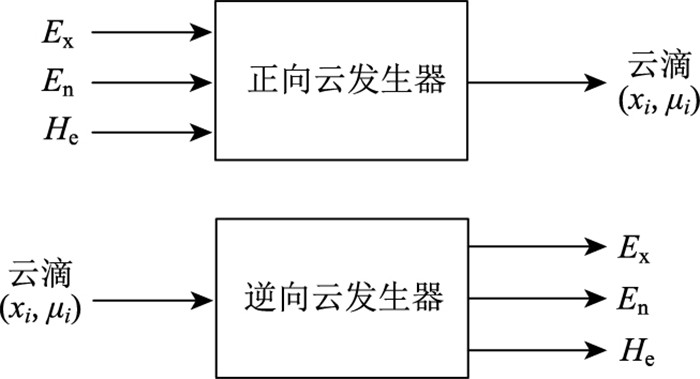
|
| 图 4 云发生器示意图 Fig. 4 Schematic diagram of cloud generator |
| |
在洞口边坡失稳风险评价中,复杂的地质条件和施工方案使得一些重要评估指标(如坡体结构、岩体风化程度、监控测量等)多以定性形式表示,而在实际工程应用中定量化评估更符合施工人员的管理需求,正向云发生器使定性指标定量化,故本研究选择正态云正向发生器构建标准云图。
标准云图的生成除3项数值特征外,还需确定隶属函数,正态云模型的隶属函数满足式(11)。
| $ \begin{gathered} \mu_i=\exp \left[-\frac{\left(x_i-E_{\mathrm{x}}\right)^2}{2 E_{\mathrm{ni}}^2}\right], \\ \left\{\begin{array}{l} E_{\mathrm{ni}} \sim N\left(E_{\mathrm{n}}, H_{\mathrm{e}}^2\right) \\ x_i \sim N\left(E_{\mathrm{x}}, E_{\mathrm{n}}^2\right) \end{array}。\right. \end{gathered} $ | (11) |
数值特征和隶属函数均确定后即可构建正态云正向云发生器生成标准云图,其在MATLAB软件中的实现过程见图 5。对照生成的标准云图即可直观看出风险等级的分布,对应每一风险等级的指标隶属度构成其模糊隶属矩阵U ={μi}。
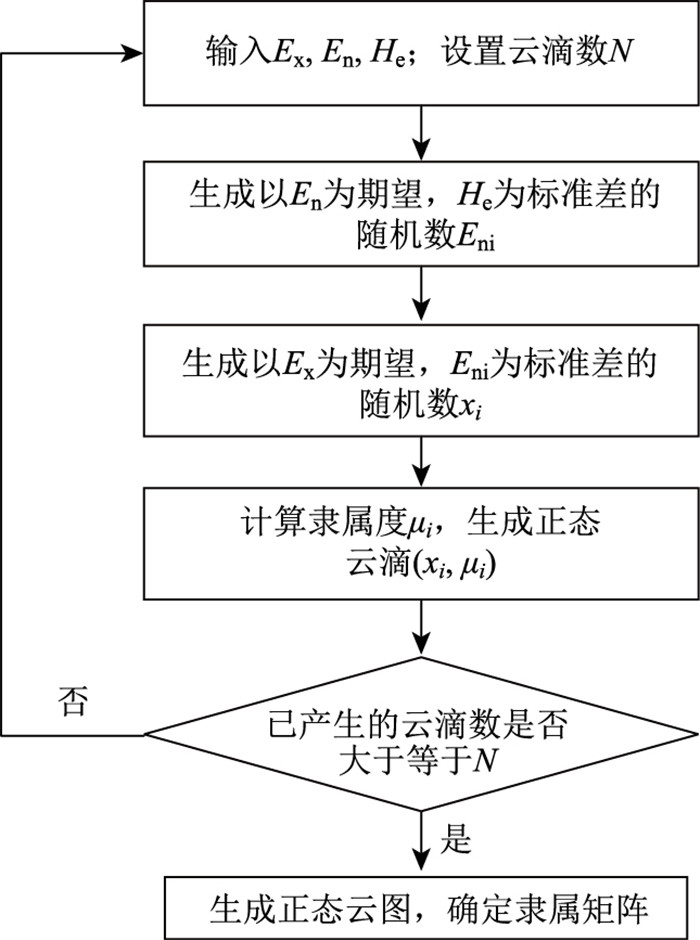
|
| 图 5 正态云正向发生器算法在MATLAB中的实现过程 Fig. 5 Implementation process of normal cloud forward generator algorithm in MATLAB |
| |
2.3 多级模糊评价
由正态云模型确定各因素的隶属度后,根据层次结构模型,由下往上对各类因素集依次进行各级模糊综合评判,综合评判集M为:
| $ \boldsymbol{M}=\boldsymbol{W}^{\circ} \boldsymbol{U}=\left[\begin{array}{llll} m_1 & m_2 & \cdots & m_p \end{array}\right], $ | (12) |
式中,W为指标组合权重集;mk为模糊综合评判指标。
则评判综合得分为:
| $ \begin{gathered} F=m_k^{\prime} \cdot v_k^{\mathrm{T}}, \\ m_k^{\prime}=\left\{\frac{m_k}{\sum\limits_{k=1}^p m_k}\right\}, (k=1, 2, \cdots, p), \end{gathered} $ | (13) |
式中,m′k为归一化后的模糊综合评判指标;vk为尺度备择集,其值取表 1中对应风险等级的最大值,即vk=[1 1.5 2.5 3.5]。将计算所得综合评判值F对照表 1即可确定风险等级。
3 山岭隧道洞口边坡失稳风险评价工程实证本研究选取云南省某山区特长隧道进口段进行洞口边坡失稳风险分析,该特长隧道全长3 940 m,起止桩号为K3+820,K7+760。工程区地处中国地势第一阶梯的川、滇山地地貌区,地势总体上呈现西北高、东南低的趋势,地貌结构以丘状高原面或分割山顶面为“基面”,基面以上为山岭、残山;基面以下为河谷、盆地。隧道总体属于河谷侵蚀构造地貌区,隧道走向K3+820~K5+000段总体为北东向,K5+000~K7+760总体为近东西向。洞室轴线与岩层走向大角度相交,未发现较大断层及活动断裂,未出现不良地质及特殊性岩土。该段山体自然坡度较缓,属低纬度高原季风气候,干湿季分明,地表水主要来自大气降水,兴发地沟常年有水,水系多属树枝状水系,局部区域呈羽状。地下水主要为基岩裂隙水和孔隙水两类。山顶植被以浅表草地为主,零星灌木生长;冲沟内草木生长相对旺盛。该段主要穿越地层为中元古界会理群黑山组,围岩等级为Ⅴ级,处强风化状态,单轴饱和抗压强度5 MPa,黏聚力0.05~0.1 MPa。因篇幅有限本研究仅列出相关项目部分情况,数据均来自该项目初设文件。
根据评价指标特征,本研究将二级评价指标中岩体风化程度、坡体结构、断层破碎带、地下水渗透力与滑动方向倾角、开挖工法、监控测量、超前预报与支护及防排水措施共8项为定性指标,其余11项均为定量指标,指标实测值根据该特长隧道项目初设文件确定。
对层次结构模型中各指标进行编号并对指标正负属性进行确定,参照表 1和《公路隧道设计规范》(JTG 3370.1—2018)(以下简称“《规范》”)对各指标的取值规定,结合专家意见构建各指标对应风险等级的基准界限值,整理见表 4。
| 一级评价指标 | 二级评价指标 | 属性 | 风险等级界限 | |||
| Ⅰ级 | Ⅱ级 | Ⅲ级 | Ⅳ级 | |||
| 地形地貌B1 | 坡高C1/m | - | [0.000 0,10.000 0] | [10.000 0,20.000 0] | [20.000 0,30.000 0] | [30.000 0,40.000 0] |
| 坡度C2/(°) | - | [0.000 0,10.000 0] | [10.000 0,25.000 0] | [25.000 0,35.000 0] | [35.000 0,45.000 0] | |
| 植被覆盖率C3/% | + | [30.000 0,45.000 0] | [15.000 0,30.000 0] | [5.000 0,15.000 0] | [0.000 0,5.000 0] | |
| 隧道偏压C4 | - | [0.000 0,0.250 0] | [0.250 0,0.500 0] | [0.500 0,0.750 0] | [0.750 0,1.000 0] | |
| 工程地质B2 | 单轴饱和抗压强度C5/MPa | + | [80.000 0,120.000 0] | [30.000 0,80.000 0] | [5.000 0,30.000 0] | [0.000 0,5.000 0] |
| 岩体风化程度C6 | - | [0.000 0,0.250 0] | [0.250 0,0.500 0] | [0.500 0,0.750 0] | [0.750 0,1.000 0] | |
| 坡体结构C7 | - | [0.000 0,0.250 0] | [0.250 0,0.500 0] | [0.500 0,0.750 0] | [0.750 0,1.000 0] | |
| 完整性系数C8/kV | + | [0.750 0,1.150 0] | [0.350 0,0.750 0] | [0.150 0,0.350 0] | [0.000 0,0.150 0] | |
| 黏聚力C9/MPa | - | [0.000 0,0.050 0] | [0.050 0,0.120 0] | [0.120 0,0.220 0] | [0.220 0,0.320 0] | |
| 内摩擦角C10/(°) | + | [35.000 0,45.000 0] | [25.000 0,35.000 0] | [15.000 0,25.000 0] | [0.000 0,15.000 0] | |
| 断层破碎带C11 | - | [0.000 0,0.250 0] | [0.250 0,0.500 0] | [0.500 0,0.750 0] | [0.750 0,1.000 0] | |
| 最大地震烈度C12 | - | [0.000 0,3.000 0] | [3.000 0,5.000 0] | [5.000 0,8.000 0] | [8.000 0,11.000 0] | |
| 水文地质B3 | 地下水渗透力与滑动方向夹角C13 | - | [0.000 0,0.250 0] | [0.250 0,0.500 0] | [0.500 0,0.750 0] | [0.750 0,1.000 0] |
| 年均降雨量C14/mm | - | [0.000 0,300.000 0] | [300.000 0,600.000 0] | [600.000 0,1 000.000 0] | [1 000.000 0,1 300.000 0] | |
| 渗透系数C15/(m·d―1) | - | [0.000 0,5.000 0] | [5.000 0,20.000 0] | [20.000 0,30.000 0] | [30.000 0,40.000 0] | |
| 施工因素B4 | 开挖工法C16 | - | [0.000 0,0.250 0] | [0.250 0,0.500 0] | [0.500 0,0.750 0] | [0.750 0,1.000 0] |
| 监控测量C17 | - | [0.000 0,0.250 0] | [0.250 0,0.500 0] | [0.500 0,0.750 0] | [0.750 0,1.000 0] | |
| 超前预报与支护C18 | - | [0.000 0,0.250 0] | [0.250 0,0.500 0] | [0.500 0,0.750 0] | [0.750 0,1.000 0] | |
| 防排水措施C19 | - | [0.000 0,0.250 0] | [0.250 0,0.500 0] | [0.500 0,0.750 0] | [0.750 0,1.000 0] | |
3.1 组合权值计算 3.1.1 确定初始判断矩阵
本研究向18位专家发放调查问卷,将德尔菲法收集所得数据代入式(2)得到B层对A层、C层对B层的初始判断矩阵为:
| $ \begin{gathered} \boldsymbol{A} =\left[\begin{array}{cccc} 1 & 1 / 3 & 1 & 1 / 3 \\ 3 & 1 & 3 & 1 / 2 \\ 1 & 1 / 3 & 1 & 1 / 3 \\ 3 & 2 & 3 & 1 \end{array}\right], \\ \boldsymbol{B} 1 =\left[\begin{array}{cccc} 1 & 1 & 3 & 1 / 2 \\ 1 & 1 & 2 & 1 / 2 \\ 1 / 3 & 1 / 2 & 1 & 1 / 3 \\ 2 & 2 & 3 & 1 \end{array}\right], \\ \boldsymbol{B} 2=\left[\begin{array}{cccccccc} 1 & 3 & 1 & 2 & 2 & 2 & 3 & 2 \\ 1 / 3 & 1 & 1 / 2 & 1 & 1 & 2 & 1 & 2 \\ 1 & 2 & 1 & 2 & 2 & 2 & 3 & 3 \\ 1 / 2 & 1 & 1 / 2 & 1 & 1 & 1 & 1 & 2 \\ 1 / 2 & 1 & 1 / 2 & 1 & 1 & 1 & 1 & 2 \\ 1 / 2 & 1 / 2 & 1 / 2 & 1 & 1 & 1 & 2 & 1 \\ 1 / 3 & 1 & 1 / 3 & 1 & 1 & 1 / 2 & 1 & 1 \\ 1 / 2 & 1 / 2 & 1 / 3 & 1 / 2 & 1 / 2 & 1 & 1 / 2 & 1 \end{array}\right], \\ \boldsymbol{B} 3=\left[\begin{array}{ccc} 1 & 2 & 1 \\ 1 / 2 & 1 & 1 / 3 \\ 1 & 3 & 1 \end{array}\right], \\ \boldsymbol{B} 4=\left[\begin{array}{cccc} 1 & 2 & 1 & 3 \\ 1 / 2 & 1 & 2 & 3 \\ 1 & 1 / 2 & 1 & 2 \\ 1 / 3 & 1 / 2 & 1 / 2 & 1 \end{array}\right] 。\end{gathered} $ |
其次进行一致性检验,由式(4)计算A,B1,B2,B3,B4的一致性指标见表 5。
| 评价指标 | A | B1 | B2 | B3 | B4 |
| Rc | 0.022 4 | 0.016 9 | 0.013 5 | 0.015 8 | 0.015 8 |
由表 5一致性检验结果可知,各判断矩阵的Rc值均小于0.1,表明判断矩阵均通过一致性检验。
3.1.2 计算评价指标权值根据式(3)~ (9)计算组合权值,权值计算结果整理见表 6。
| 一级评价指标 | 主观权值 | 二级评价指标 | 主观权值 | 客观权值 | 组合权值 |
| B1 | 0.123 6 | C1 | 0.030 0 | 0.029 7 | 0.029 9 |
| C2 | 0.026 4 | 0.031 7 | 0.029 0 | ||
| C3 | 0.013 2 | 0.024 8 | 0.019 0 | ||
| C4 | 0.050 4 | 0.034 2 | 0.042 4 | ||
| B2 | 0.311 8 | C5 | 0.067 2 | 0.051 3 | 0.059 3 |
| C6 | 0.035 2 | 0.120 3 | 0.077 4 | ||
| C7 | 0.067 2 | 0.110 1 | 0.088 5 | ||
| C8 | 0.035 2 | 0.064 4 | 0.049 7 | ||
| C9 | 0.035 2 | 0.096 3 | 0.065 5 | ||
| C10 | 0.032 0 | 0.078 6 | 0.055 1 | ||
| C11 | 0.025 6 | 0.103 6 | 0.064 3 | ||
| C12 | 0.022 4 | 0.103 2 | 0.062 5 | ||
| B3 | 0.123 6 | C13 | 0.046 8 | 0.011 9 | 0.029 5 |
| C14 | 0.020 4 | 0.015 9 | 0.018 2 | ||
| C15 | 0.052 8 | 0.011 9 | 0.032 5 | ||
| B4 | 0.441 0 | C16 | 0.158 4 | 0.026 0 | 0.092 7 |
| C17 | 0.123 2 | 0.033 5 | 0.078 7 | ||
| C18 | 0.101 2 | 0.025 6 | 0.063 7 | ||
| C19 | 0.057 2 | 0.026 9 | 0.042 2 |
3.2 基于MATLAB数值模拟的云模型计算 3.2.1 确定标准云数值
将表 4各指标对应风险等级的基准界限值代入式(10),计算19项二级评价指标在4类风险等级下对应的标准云数值特征,结果见表 7。
| 指标 | 标准云数值特征 | |||
| Ⅰ级 | Ⅱ级 | Ⅲ级 | Ⅳ级 | |
| C1 | (5.000 0,4.246 3,0.400 0) | (15.000 0,4.246 3,0.400 0) | (25.000 0,4.246 3,0.400 0) | (35.000 0,4.246 3,0.400 0) |
| C2 | (5.000 0,4.246 3,0.400 0) | (17.500 0,6.369 4,0.400 0) | (30.000 0,6.369 4,0.400 0) | (40.000 0,4.246 3,0.400 0) |
| C3 | (37.500 0,6.369 4,0.600 0) | (22.500 0,6.369 4,0.600 0) | (10.000 0,4.246 3,0.400 0) | (2.500 0,4.246 3,0.400 0) |
| C4 | (0.125 0,0.106 2,0.010 0) | (0.375 0,0.106 2,0.010 0) | (0.625 0,0.106 2,0.010 0) | (0.875 0,0.106 2,0.010 0) |
| C5 | (100.000 0,16.985 1,1.600 0) | (55.000 0,21.231 4,2.100 0) | (17.500 0,10.615 7,1.000 0) | (2.500 0,2.123 1,0.200 0) |
| C6 | (0.125 0,0.106 2,0.010 0) | (0.375 0,0.106 2,0.010 0) | (0.625 0,0.106 2,0.010 0) | (0.875 0,0.106 2,0.010 0) |
| C7 | (0.125 0,0.106 2,0.010 0) | (0.375 0,0.106 2,0.010 0) | (0.625 0,0.106 2,0.010 0) | (0.875 0,0.106 2,0.010 0) |
| C8 | (0.950 0,0.169 9,0.020 0) | (0.550 0,0.169 9,0.020 0) | (0.250 0,0.084 9,0.008 0) | (0.075 0,0.063 7,0.006 0) |
| C9 | (0.025 0,0.212 3,0.020 0) | (0.085 0,0.029 7,0.003 0) | (0.170 0,0.042 5,0.004 0) | (0.270 0,0.042 5,0.004 0) |
| C10 | (40.000 0,4.246 3,0.400 0) | (30.000 0,4.246 3,0.400 0) | (20.000 0,4.246 3,0.400 0) | (7.500 0,6.369 4,0.600 0) |
| C11 | (0.125 0,0.106 2,0.010 0) | (0.375 0,0.106 2,0.010 0) | (0.625 0,0.106 2,0.010 0) | (0.875 0,0.106 2,0.010 0) |
| C12 | (1.500 0,1.273 9,0.010 0) | (4.000 0,0.849 3,0.080 0) | (6.500 0,1.273 9,0.100 0) | (9.500 0,1.273 9,0.100 0) |
| C13 | (0.125 0,0.106 2,0.010 0) | (0.375 0,0.106 2,0.010 0) | (0.625 0,0.106 2,0.010 0) | (0.875 0,0.106 2,0.010 0) |
| C14 | (150.000 0,127.389 0,12.700 0) | (450.000 0,127.389 0,12.700 0) | (800.000 0,169.851 0,17.000 0) | (1 150.000 0,127.389 0,12.700 0) |
| C15 | (2.500 0,2.123 1,0.200 0) | (12.500 0,6.369 4,0.600 0) | (25.000 0,4.246 3,0.400 0) | (35.000 0,4.246 3,0.400 0) |
| C16 | (0.125 0,0.106 2,0.010 0) | (0.375 0,0.106 2,0.010 0) | (0.625 0,0.106 2,0.010 0) | (0.875 0,0.106 2,0.010 0) |
| C17 | (0.125 0,0.106 2,0.010 0) | (0.375 0,0.106 2,0.010 0) | (0.625 0,0.106 2,0.010 0) | (0.875 0,0.106 2,0.010 0) |
| C18 | (0.125 0,0.106 2,0.010 0) | (0.375 0,0.106 2,0.010 0) | (0.625 0,0.106 2,0.010 0) | (0.875 0,0.106 2,0.010 0) |
| C19 | (0.125 0,0.106 2,0.010 0) | (0.375 0,0.106 2,0.010 0) | (0.625 0,0.106 2,0.010 0) | (0.875 0,0.106 2,0.010 0) |
由表 7及借助MATLAB工具软件,绘制出各指标的标准云图。当单因素云滴数量不少于3 000个时隶属度结果误差小于5%[28],故本研究将云滴数N设置为3 000。因篇幅所限,本研究从地形地貌、地质条件、气候水文和施工因素4项一级评价指标中各选择两项二级评价指标作为代表性指标展示标准云图,8项代表性指标标准云图见图 6。

|
| 图 6 部分二级评价指标正态标准云图 Fig. 6 Normal standard cloud charts of partial secondary evaluation indicators |
| |
由图 6(a)和图 6(b)看出,正向指标如植被覆盖率单因素标准云图自左向右风险等级逐步提高,由极不安全提升至安全,表明植被覆盖率越高,边坡失稳可能性越小;负向指标如坡高自左向右风险等级逐步降低,由安全降低至极不安全风险等级,表明坡体高度越大,边坡失稳可能性越大。
3.2.2 计算隶属度将标准云的数值特征及指标实测值代入式(11)计算各指标所属每一风险等级的隶属度,每一风险等级对应的隶属度构成模糊隶属矩阵,如下。
| $ \begin{aligned} \boldsymbol{R}_{B 1} & =\left[\begin{array}{lllll} 0.009\;2 & 0.779\;1 & 0.257\;0 & 0.000\;3 \\ 0.000\;8 & 0.859\;9 & 0.368\;5 & 0.000\;0 \\ 0.074\;9 & 0.996\;9 & 0.009\;2 & 0.009\;2 \\ 0.106\;0 & 0.972\;7 & 0.035\;0 & 0.000\;0 \end{array}\right] \\ \boldsymbol{R}_{B 2} & =\left[\begin{array}{lllll} 0.000\;0 & 0.105\;8 & 0.779\;1 & 0.002\;0 \\ 0.000\;0 & 0.106\;0 & 0.972\;7 & 0.035\;0 \\ 0.035\;0 & 0.972\;7 & 0.106\;0 & 0.000\;0 \\ 0.000\;0 & 0.062\;6 & 0.499\;7 & 0.500\;0 \\ 0.972\;7 & 0.499\;4 & 0.018\;6 & 0.000\;0 \\ 0.000\;0 & 0.105\;8 & 0.972\;7 & 0.105\;8 \\ 0.500\;2 & 0.002\;0 & 0.000\;0 & 0.000\;0 \\ 0.925\;9 & 0.062\;6 & 0.002\;0 & 0.000\;0 \end{array}\right] \\ \boldsymbol{R}_{B 3} & =\left[\begin{array}{lllll} 0.972\;7 & 0.035\;0 & 0.000\;0 & 0.000\;0 \\ 0.000\;7 & 0.023\;0 & 1.000\;0 & 0.023\;0 \\ 0.859\;9 & 0.594\;1 & 0.000\;0 & 0.000\;0 \end{array}\right] \\ \boldsymbol{R}_{B 4} & =\left[\begin{array}{lllll} 0.947\;1 & 0.128\;8 & 0.000\;1 & 0.000\;0 \\ 0.998\;9 & 0.056\;0 & 0.000\;0 & 0.000\;0 \\ 0.972\;7 & 0.106\;0 & 0.000\;0 & 0.000\;0 \\ 0.874\;5 & 0.185\;3 & 0.000\;2 & 0.000\;0 \end{array}\right] 。\end{aligned} $ |
组合权值和隶属度矩阵确定后使用模糊理论对边坡失稳风险等级值进行计算,将二级评价指标的组合权值和模糊隶属矩阵代入式(12)对洞口边坡失稳风险进行一级模糊评判,计算得到一级模糊评判集
| $ \boldsymbol{M}_1=\left[\begin{array}{lllll} 0.029\;9 & 0.029\;9 & 0.029\;9 & 0.009\;2 \\ 0.059\;3 & 0.059\;3 & 0.059\;3 & 0.059\;3 \\ 0.029\;5 & 0.029\;5 & 0.029\;5 & 0.023\;0 \\ 0.092\;7 & 0.092\;7 & 0.000\;2 & 0.000\;0 \end{array}\right] . $ |
将一级评价指标的组合权值和一级模糊评判集代入式(12)对洞口边坡失稳进行二级模糊评判,计算得到二级模糊评判集
| $ \boldsymbol{M}_2=\left[\begin{array}{l} 0.092\;7 \\ 0.092\;7 \\ 0.059\;3 \\ 0.059\;3 \end{array}\right] 。$ |
将二级模糊综合评判集M2代入式(13)归一化后计算得到洞口边坡失稳风险的综合评判得分
| $ \begin{gathered} \boldsymbol{F}=m_k^{\prime} \cdot \boldsymbol{v}_k^{\mathrm{T}}=\left[\begin{array}{lllll} 0.304\;9 & 0.304\;9 & 0.195\;1 & 0.195\;1 \end{array}\right] \cdot \\ \left[\begin{array}{c} 1 \\ 1.5 \\ 2.5 \\ 3.5 \end{array}\right]=1.932\;7 。\end{gathered} $ |
从以上计算可知,该特长隧道洞口失稳的模糊综合评判指标为F=1.932 7,对照表 1可知,其风险等级值在1.5~2.5范围区间内,洞口边坡失稳风险等级为Ⅱ级。
纵观该隧道洞口段评价结果,虽属比较安全,但由表 6中组合权值可知,风险因素按影响程度从大到小排序为:开挖工法(0.092 7)、坡体结构(0.088 5)、监控测量(0.078 7)、岩体风化程度(0.077 4)、黏聚力(0.065 5)、断层破碎带(0.064 3)、超前预报与支护(0.063 7)、最大地震烈度(0.062 5)、单轴饱和抗压强度(0.059 3)、内摩擦角(0.055 1)、完整性系数(0.049 7)、隧道偏压(0.042 4)、防排水措施(0.042 2)、渗透系数(0.032 5)、坡高(0.029 9)、地下水渗透力与滑动方向夹角(0.029 5)、坡度(0.029 0)、植被覆盖率(0.019 0)、年均降雨量(0.018 2),可见开挖工法、坡体结构、监控测量及岩体风化程度对洞口段边坡失稳影响较大,需引起重视。
3.4 模型对比验证为验证模型计算结果有效性,本研究将结果与《指南》中推荐的风险矩阵法、模糊综合分析法及另选择物元可拓法3种模型的评价结果进行对比。风险矩阵法[29]由专家对概率等级和损失等级进行评定,根据专家评定结果参照风险矩阵图即可读出风险等级值。在模糊综合分析法[30]隶属度函数的选择中,由于本研究洞口边坡失稳风险等级划分为4级,故选择三角分布函数作为定量指标的隶属度函数,模糊综合评判值为1.727 6。物元可拓法[31]通过计算指标与待评物元各等级间的关联度进行评价,关联度的绝对值越小,与某一风险等级的相关性越大,表示越接近此等级,评价结果见表 8。
| 评价模型 | 风险矩阵法 | 模糊综合分析法 | 物元可拓法 | CRITIC组合赋权-正态云模型 | |||
| 评价结果 | Ⅰ级 | 1.727 6 | Ⅰ级 | Ⅱ级 | Ⅲ级 | Ⅳ级 | 1.932 7 |
| ―0.321 4 | ―0.208 5 | ―0.326 8 | ―0.412 5 | ||||
| 风险等级 | Ⅰ级 | Ⅱ级 | Ⅱ级 | Ⅱ级 | |||
由表 8可知,本研究模型计算结果与模糊综合分析法和物元可拓法评价结果一致,均为Ⅱ级,属比较安全;风险矩阵法评价结果为Ⅰ级,属于安全,风险事件发生的概率可忽略。风险矩阵法与其他方法的评价结果有偏差,主要与专家确定概率等级和损失等级有关,受主观影响较大。
3.5 现场施工对比验证根据地勘资料和现场调查情况可知,拟建隧道洞口段山体坡度10°~20°。年均降雨量为787.8 mm,地表水蒸发旺盛,地下水为基岩裂隙水和孔隙水两类,pH值为7.18~7.52,对混凝土结构有微腐蚀性,总体来说,地形地貌和水文地质条件较好,对边坡失稳风险影响较小。在工程地质方面,洞口段主要为Ⅴ级围岩,处强风化状态,强风化层厚一般5~10 m,局部10~20 m。隧道主要穿越地层为中元古界会理群黑山组,分布于桩号K3+820~K7+167.9,主要成分为绢云千枚岩、深灰色变质砂岩等;千枚岩属易滑地层,其强风化带岩体呈碎片状或粉末状,砂岩强风化后呈砂砾状,岩体松散破碎,整体稳定性差,施工时边坡易发生滑塌现象。在施工方面,开挖边坡主要为顺向坡,施工因素对于边坡稳定性扰动较大,若开挖顺序与工法选取不当,极易发生洞口边坡失稳。另外,K3+820~K3+840区段路线内侧分布较多坡面浮石,在雨季易产生落石,同时岩体在饱水条件下强度显著降低,雨季开挖时边坡失稳风险较大。
鉴于此,并依据该隧道洞口边坡失稳风险预评价结论,建议选择端墙式洞门,使用CD法,采取1∶1坡比开挖,避免雨季施工;在开挖过程中,布设混凝土保护层,采取超前预报、大管棚超前支护等措施,同时做好防排水。由现场施工反馈得知,K3+820~K3+830区段边坡临江侧进口处覆土层厚度不均,约为1~4 m,存在偏压情况;围岩有轻微变形,最大变形量为12.3 cm;洞口边坡发生轻微滑塌,土方量约为70 m3。滑塌发生后施工人员及时支护加固及实施监测,未造成严重事故,洞口其余区段边坡未出现失稳。由此看出,本研究基于博弈论的CRITIC组合赋权-正态云评价模型对于该隧道洞口边坡失稳风险的预评价结果为Ⅱ级(属可接受风险)较为准确,模型具有可预测性和适用性,对隧道边坡失稳风险等级判断及指导施工有一定的现实意义。
4 结论本研究基于博弈论的CRITIC组合赋权-正态云评价模型,对隧道洞口边坡失稳风险进行评价,取得如下研究结论:
(1) 引入“敏感性”概念,对隧道洞口边坡失稳影响因素进行筛选,建立边坡失稳风险评价指标体系,融合AHP法和CRITIC法,使用博弈论对各评价指标进行组合赋权,克服了传统评估方法中指标权值客观性不足的问题。
(2) 给出指标对应各安全等级的基准界限值,使用云模型将定性指标定量化,弥补了定性指标的不确定性,指标隶属度的准确性得以提升。
(3) 结合云南省某特长隧道实例,该模型评价结论与风险矩阵法、模糊层次分析法、物元可拓法等3种方法计算分析一致,也与施工结果相符合,验证了该模型的有效性和可靠性。
| [1] |
李洋溢, 何克扬. 大跨度隧道洞口滑坡形成机制及处治方案研究[J]. 公路, 2022, 67(9): 464-469. LI Yangyi, HE Keyang. Study on the formation mechanism and treatment plan of landslide at the entrance of large span tunnel[J]. Highway, 2022, 67(9): 464-469. |
| [2] |
KALOGERAKI M, ANTONIOU F. Improving risk assessment for transporting dangerous goods through european road tunnels: A delphi study[J].
Systems, 2021, 9(4): 80.
|
| [3] |
刘栗昊, 缪林昌. 基于联合灰色关联分析的土质边坡稳定性预测[J]. 公路交通科技, 2022, 39(10): 32-39. LIU Lihao, LIAO Linchang. Prediction of soil slope stability based on conjoint grey correlation analysis[J]. Journal of Highway and Transportation Research and Development, 2022, 39(10): 32-39. DOI:10.3969/j.issn.1002-0268.2022.10.005 |
| [4] |
SHI F L, CAI S. Research on safety evaluation and system development of tunnel lining based on set pair analysis[J].
Journal of Physics: Conference Series, 2023, 2470(1): 012021.
DOI:10.1088/1742-6596/2470/1/012021 |
| [5] |
HUANG J L, ZENG X Y, FU J, et al. Safety risk assessment using a BP neural network of high cutting slope construction in high-speed railway[J].
Buildings, 2022, 12(5): 598.
|
| [6] |
张志雄, 叶雪云, 殷志强, 等. 基于FAHP法的连续多跨渡槽拆除爆破安全评价[J]. 中国安全科学学报, 2020, 30(11): 67-74. ZHANG Zhixiong, YE Xueyun, YIN Zhiqiang, et al. Safety evaluation of continuous multi-span aqueduct 's demolition blasting based on FAHP method[J]. China Safety Science Journal, 2020, 30(11): 67-74. |
| [7] |
刘秀, 李文洋. 基于熵权物元可拓模型的路堑边坡安全性评价[J]. 公路交通科技, 2022, 39(11): 49-55. LIU Xiu, LI Wenyang. Evaluation on safety of cutting slope based on entropy weight matter-element extension model[J]. Journal of Highway and Transportation Research and Development, 2022, 39(11): 49-55. DOI:10.3969/j.issn.1002-0268.2022.11.007 |
| [8] |
冯忠居, 朱彦名, 高雪池, 等. 基于熵权-灰关联法的岩质开挖边坡安全评价模型[J]. 交通运输工程学报, 2020, 20(2): 55-65. FENG Zhongju, ZHU Yanming, GAO Xuechi, et al. Safety evaluation model of excavating rock slope based on entropy-grey correlation method[J]. Journal of Transportation Engineering, 2020, 20(2): 55-65. |
| [9] |
YANG X, HAO Z, MA G, et al. Research on slope stability evaluation based on improved set pair analysis method: A case of tonglvshan open-pit mine[J].
Shock and Vibration, 2021, 2021: 6713581.
DOI:10.1155/2021/6713581 |
| [10] |
李国良, 王磊, 杨晓严, 等. 中国交通基础设施发展水平比较研究[J]. 公路交通科技, 2021, 38(11): 97-105. LI Guoliang, WANG Lei, YANG Xiaoyan, et al. Comparative study on development level of transport infrastructure in China[J]. Journal of Highway and Transportation Research and Development, 2021, 38(11): 97-105. DOI:10.3969/j.issn.1002-0268.2021.11.012 |
| [11] |
DIAKOULAKI D, MAVROTAS G, PAPAYANNAKIS L. Determining objective weights in multiple criteria problems: The critic method[J].
Computers & Operations Research, 1995, 22(7): 763-770.
|
| [12] |
李德毅, 刘常昱, 淦文燕. 正态云模型的重尾性质证明[J]. 中国工程科学, 2011, 13(4): 20-23. LI Deyi, LIU Changyu, GAN Wenyan. Proof of the heavy-tailed property of normal cloud model[J]. Strategic Study of CAE, 2011, 13(4): 20-23. |
| [13] |
叶琼, 李绍稳, 张友华, 等. 云模型及应用综述[J]. 计算机工程与设计, 2011, 32(12): 4198-4201. YE Qiong, LI Shaowen, ZHANG Youhua, et al. Cloud model and application overview[J]. Computer Engineering and Design, 2011, 32(12): 4198-4201. |
| [14] |
WANG C, LI J W, WANG H. Fuzzy risk assessment of tunnels ' undercrossing existing structures[J].
Mathematical Problems in Engineering, 2022, 2022: 4812245.
DOI:10.1155/2022/4812245 |
| [15] |
LIN C J, ZHANG M, LI L P, et al. Risk assessment of tunnel construction based on improved cloud model[J].
Journal of Performance of Constructed Facilities, 2020, 34(3): 04020028.
DOI:10.1061/(ASCE)CF.1943-5509.0001421 |
| [16] |
PENG Y X, WU L, ZUO Q J, et al. Risk assessment of water inrush in tunnel through water-rich fault based on AHP-cloud model[J].
Geomatics, Natural Hazards and Risk, 2020, 11(1): 301-317.
|
| [17] |
赵岩. 基于主成分分析-云模型的黄土隧道施工稳定性评估[J]. 隧道建设(中英文), 2022, 42(9): 1529-1536. ZHAO Yan. Stability evaluation of loess tunnel during construction based on principal component analysis-cloud model[J]. Tunnel Construction, 2022, 42(9): 1529-1536. |
| [18] |
严彬华, 王万平, 刘瑞辉, 等. 风积沙地层隧道洞口边坡稳定性分析[J]. 公路, 2022, 67(5): 267-271. YAN Binhua, WANG Wanping, LIU Ruihui, et al. Stability analysis of tunnel portal slope in windblown sand strata[J]. Highway, 2022, 67(5): 267-271. |
| [19] |
张翾, 汪成兵, 周宁, 等. 某黄土隧道洞口段边坡坍塌机理分析[J]. 地下空间与工程学报, 2015, 11(增1): 307-312. ZHANG Yan, WANG Chengbing, ZHOU Ning, et al. Analysis on mechanism of slide-slope collapse at a loess tunnel entrance[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(S1): 307-312. |
| [20] |
宋开忠, 侯哲生, 刘媛媛. 内外组合施工扰动下隧道洞口边坡稳定性分析[J]. 水利与建筑工程学报, 2020, 18(6): 208-212. SONG Kaizhong, HOU Zhesheng, LIU Yuanyuan. Stability analysis of tunnel entrance slope under disturbance of internal and external combined construction[J]. Journal of Water Resources and Architectural Engineering, 2020, 18(6): 208-212. |
| [21] |
陈红, 周继彪, 王建军, 等. 公路隧道运行环境安全评价指标与方法[J]. 长安大学学报(自然科学版), 2013, 33(4): 54-61, 74. CHEN Hong, ZHOU Jibiao, WANG Jianjun, et al. Safety evaluation indexes and method for traffic environment of highway tunnels[J]. Journal of Chang 'an University (Natural Science Edition), 2013, 33(4): 54-61, 74. |
| [22] |
SAATY T L. Applications of analytical hierarchies[J].
Mathematics and Computers in Simulation, 1979, 21(1): 1-20.
|
| [23] |
LINSTONE H A, TUROFF M E. The Delphi Method[M].
Boston: Addison-Wesley Publishing Company, 1975.
|
| [24] |
王晶晶, 孙宁, 张营, 等. 基于AHP的危化品运输企业风险预警研究[J]. 物流工程与管理, 2019, 41(6): 120-121. WANG Jingjing, SUN Ning, ZHANG Ying, et al. Research on risk pre-warning method of dangerous chemical transportation enterprises based on AHP[J]. Logistics Engineering and Management, 2019, 41(6): 120-121. |
| [25] |
范泽. 基于层次分析法的互通方案多目标优选研究[J]. 公路交通科技, 2023, 40(5): 202-210. FAN Ze. Study on multi-objective optimization of interchange scheme based on AHP[J]. Journal of Highway and Transportation Research and Development, 2023, 40(5): 202-210. DOI:10.3969/j.issn.1002-0268.2023.05.027 |
| [26] |
战琦, 周炜, 李文亮, 等. 基于组合赋权的车辆智能换道避障功能模糊综合评价[J]. 公路交通科技, 2023, 40(1): 236-244. ZHAN Qi, ZHOU Wei, LI Wenliang, et al. Fuzzy comprehensive evaluation on vehicle intelligent obstacle avoidance function by lane changing based on combination weighting[J]. Journal of Highway and Transportation Research and Development, 2023, 40(1): 236-244. DOI:10.3969/j.issn.1002-0268.2023.01.027 |
| [27] |
FUDENBERG D, TIROLE J. Game theory[M].
Cambridge: MIT Press, 1991.
|
| [28] |
LIN C J, ZHANG M, LI L P, et al. Risk assessment of tunnel construction based on improved cloud model[J].
Journal of Performance of Constructed Facilities, 2020, 34(3): 04020028.
DOI:10.1061/(ASCE)CF.1943-5509.0001421 |
| [29] |
葛及, 郭迪. 基于风险矩阵法的化工企业综合安全评价模型及其应用[J]. 安全与环境学报, 2016, 16(5): 21-24. GE Ji, GUO Di. Comprehensive safety evaluation model of the chemical enterprises based on the risk matrix method and its application[J]. Journal of Safety and Environment, 2016, 16(5): 21-24. |
| [30] |
刘超, 刘刚, 许崇帮, 等. 基于模糊理论的隧道服役性能评价方法研究[J]. 公路交通科技, 2022, 39(8): 142-150, 165. LIU Chao, LIU Gang, XU Chongbang, et al. Study on service performance evaluation method for tunnel based on fuzzy theory[J]. Journal of Highway and Transportation Research and Development, 2022, 39(8): 142-150, 165. DOI:10.3969/j.issn.1002-0268.2022.08.019 |
| [31] |
裴兴旺, 李慧民, 李文龙, 等. 基于熵权物元可拓的桥梁检测作业危险性评价[J]. 中国安全科学学报, 2019, 29(8): 42-48. PEI Xingwang, LI Huimin, LI Wenlong, et al. Risk assessment of bridge detection operation based on entropy weight and matter-element extension theory[J]. China Safety Science Journal, 2019, 29(8): 42-48. |
 2025, Vol. 42
2025, Vol. 42



 ,
,