扩展功能
文章信息
- 赛志毅, 党王辉, 郭建民, 白光耀, 牛艳伟.
- SAI Zhiyi, DANG Wanghui, GUO Jianmin, BAI Guangyao, NIU Yanwei
- 单箱双室波形钢腹板箱梁腹板受力差异性分析与实桥试验
- Web force difference analysis on single-box double-cell box girder with corrugated steel webs and actual bridge experiment
- 公路交通科技, 2025, 42(7): 133-143
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(7): 133-143
- 10.3969/j.issn.1002-0268.2025.07.014
-
文章历史
- 收稿日期: 2023-06-13
2. 长安大学 公路学院,陕西 西安 710064;
3. 山东省交通规划设计院集团有限公司,山东 济南 250014
2. School of Highway, Chang'an University, Xi'an, Shaanxi 710064, China;
3. Shandong Provincial Communications Planning and Design Institute Group Co., Ltd., Jinan, Shandong 250014, China
波形钢腹板箱梁将传统混凝土箱梁桥的腹板替代为质量更轻、强度与刚度更大的波形钢腹板,不仅保留了传统箱梁的各种优点,同时遵循桥梁设计的原则在安全、适用、经济、美观4个方面进行了相应改善。例如提高抗震性,充分发挥材料性能,改善无混凝土腹板的一系列耐久性问题,减少总造价和工期,具有更美的视觉感受。随着社会和经济的不断发展和对交通舒适性和安全性需求的不断提高,波形钢腹板桥逐渐向大跨径、宽幅化的趋势发展。近5 a内新建成的波形钢腹板桥以连续箱梁桥为主,其主跨范围为120~188 m,宽度范围为13~33 m,部分桥梁如表 1所示。其广泛应用的同时也有许多亟待解决的工程结构问题随之而来。
| 名称 | 跨径/m | 年份 |
| 曲港南水北调大桥 | 88+151+88 | 2018 |
| 浙江奉化江大桥 | 100+160+100 | 2018 |
| 陕西梁渠沟特大桥 | 75+2×140+75 | 2019 |
| 江西南昌潘余特大桥 | 83+152+83 | 2021 |
| 九绵高速蜈蚣口大桥 | 88+160+88 | 2021 |
| 江门银州湖特大桥 | 89+162+89 | 2021 |
| 广西飞龙特大桥 | 100+2×185+100 | 2021 |
| 杭绍甬曹娥江特大桥 | 50.6+78.0+188.0+50.6+78.0 | 2022 |
国内外学者对波形钢腹板桥的各项性能进行了大量研究,主要集中在抗剪性能[1-8]、承载能力[9-11]、弯扭性能[12-17]、参数设计[18-21]、施工方案[22-27]、横向受力[28-30]、计算方法[31]及长期受力[32]等方面。王超[4]、贾慧娟[5]、曹海洋[6]研究了变高度波形钢腹板桥梁高变化下的剪应力计算公式及分布规律;Guo[12]、李运生[13]、Lukin[14]、冉川[15]、王亚萍[16]、杨轩宇[17]对波形钢腹板的弯扭性能进行了研究;梁铎[24]、祝丰平[25]、宋胜录[26]、舒宏生[27]对波形钢腹板桥的工艺技术进行了创新,提高了施工可控性和安全性。刘旭政[28]、程坤[29]、赵品[30]深入研究了波形钢腹板桥的横向受力分布宽度;Zhang[31]采用Zig-Zag变形理论推导出一种适用于波形钢腹板组合桥的新型研究方法,可准确预测其变形和应力情况;Motlagh[32]对预应力波形钢腹板组合梁桥的长期性能进行了研究并修正了现有的研究模型。
对于单箱双室波形钢腹板箱梁桥而言,现有的研究缺乏对施工动态变化过程中各腹板受力分配状况的研究,忽略了一些客观存在的影响因素, 例如腹板高度的差异。在计算中通常默认顶板水平无横坡,腹板高度一致,但在双幅箱梁桥的实际工程设计中为达到排水或超高的目的,左右两幅单向坡的横坡设置通常是改变腹板的高度,通过高度差实现桥面倾斜。腹板所处位置及钢-混结合段等因素亦会对波形钢腹板箱梁桥各腹板的受力性能产生一定的影响,但这一问题至今鲜有研究。
因此本研究以提高波形钢腹板箱梁桥施工及成桥状态的安全性为目的,基于实际工程采用ABAQUS的生死单元法对全桥施工到成桥过程进行有限元模拟分析,围绕各腹板的差异性对一具有非等高度腹板的单箱双室波形钢腹板箱梁桥受力分配的影响进行研究。
1 研究对象本研究以一典型的波形钢腹板桥—减河大桥为研究对象,其跨径、桥宽及结构形式均属于中国当前新建波形钢腹板桥常用的方案,具有十分重要的研究意义,可为中国新建或计划建成的波形钢腹板桥提供普适参考。
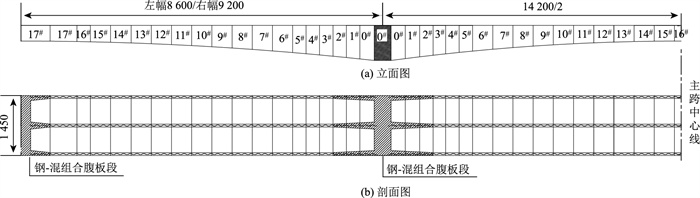
减河大桥位于京台高速公路德州至齐河段,为跨越减河而建。上部结构采用双幅式单箱双室波形钢腹板箱梁,左幅跨径为(86+142+86)m,右幅跨径为(92+142+86)m,设计行车速度为120 km/h,桥梁荷载等级为一级公路,单幅桥宽为0.5+19.5+0.5=20.5 m,两幅全宽为42 m。设置双向2%横坡用于桥面排水,由箱梁腹板不同高度形成,梁高以1.8次抛物线变化,总体布置如图 1所示。图中D为对称悬臂施工号块,B为边跨现浇号块,ZH为中跨合龙号块,BH为边跨合龙号块。

|
| 图 1 减河大桥立面布置图(单位:cm) Fig. 1 Elevation layout of Jianhe bridge (Unit: cm) |
| |
箱梁支架现浇0#块节段长为10.8 m,在主墩托架上浇注。两侧各有15个悬浇节段,节段长度为5×3.2 m和10×4.8 m。1#~15#梁段采用挂篮悬臂浇注施工,主桥共有3个合龙段,即1个中跨合龙段和2个边跨合龙段,合龙段长均为3.2 m,在吊架上浇注。边跨现浇段长为13.3 m,右幅小桩号侧现浇段长为19.3 m,在支架上浇注。波形腹板采用1600型波型钢板,钢材采用Q355D。箱梁钢-混结合段的布置如图 2所示。
|
| 图 2 结构示意图(单位:cm) Fig. 2 Structure diagram (unit: cm) |
| |
此桥左右两幅对称采用2%的横坡,用于桥面排水,通过调整腹板高度进行实现。因此在设计与计算中应考虑腹板高度的不同,以及腹板自身位置和钢-混结合段的影响。因此需要更为深入地研究腹板差异性对其受力分配的影响以提高结构的安全性和可靠性。
2 理论分析为了更为清晰准确地探究腹板差异性对波形钢腹板箱梁桥的受力分配影响情况,本研究运用ABAQUS软件,基于减河大桥实际工程,采用有限元分析方法进行实桥模型的建立。利用生死单元法模拟了不同施工工况,并对各种工况下的计算结果进行分析。
2.1 有限元模型的建立参照实际桥梁,本研究采用ABAQUS有限元软件建立右幅的箱梁模型,尺寸为(92+142+86) m,模型空间中的x为横桥向方向,y为竖桥向方向,z为顺桥向方向。采用C3D8R三维实体单元模拟混凝土及波形钢腹板。混凝土采用C55,波形钢腹板采用Q355D,部件尺寸和材料性能均符合实际桥梁的设计。全桥模型的边界条件按照实际桥梁的施工过程进行设置,涉及到结构体系转换和成桥后的支座设置,其边界条件如表 2所示。
| 施工阶段 | 施工号块 | 0#块 | 边跨现浇段 |
| 对称悬浇 | 0#~11# | 临时固结 | — |
| 对称悬浇、边跨现浇段 | 12#~15#,17# | 临时固结 | 搭设支架并设置临时纵向约束 |
| 单悬臂 | 16# | 临时固结 | 拆除支架及临时纵向约束 |
| 成桥 | 16# | 拆除临时固结 | 拆除支架及临时纵向约束 |
本研究主要研究腹板的差异性对箱梁受力的影响情况,因此在有限元模型中仅对其施加恒载,可进行更为方便有效的研究。同时为保证计算结果的精准性,设置单元尺寸为240 mm。
2.2 计算工况为探究腹板差异性影响下,波形钢腹板箱梁桥在施工和成桥状态的受力特点,本研究运用ABAQUS有限元软件中的生死单元法对桥梁的全施工过程进行模拟。
计算工况基本分为双悬臂阶段、单悬臂阶段、成桥阶段。双悬臂阶段为对称悬臂施工阶段;单悬臂阶段为边跨已合龙但中跨尚未合龙的施工状态;成桥阶段为边跨和中跨均已合龙,体系转换完毕之后的状态,计算工况如表 3所示。
2.3 计算结果分析
按照表 3中的计算工况,在ABAQUS有限元软件中采用生死单元法对实桥模型进行计算分析,分别得到模型在恒载作用下双悬臂、单悬臂、成桥3种状态的各项力学性能。本研究着重研究了纵向弯矩、截面剪力及纵向应力受腹板差异性的影响。
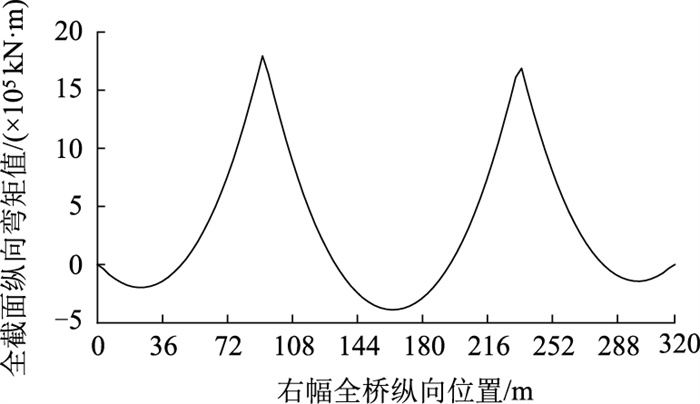
2.3.1 全桥纵向弯矩分布基于有限元软件对恒载作用下全桥模型成桥阶段的纵向内力进行计算分析,右幅为(92+142+86)m,其横截面的纵向弯矩沿桥梁纵向分布情况如图 3所示。
|
| 图 3 纵向弯矩分布 Fig. 3 Longitudinal bending moment distribution |
| |
通过计算得到的纵向弯矩值可见ABAQUS有限元软件可准确合理地模拟出变高度连续梁桥的纵向受力规律,并且在腹板差异的影响下,波形钢腹板连续箱梁的纵向弯矩分布规律未见较大变化, 即由恒载引起的截面弯矩,在跨中处弯矩最小,两边跨处弯矩较小,2个墩顶处弯矩最大,大体呈现从两侧边跨向墩顶弯矩逐渐增大,在墩顶处达到峰值,随后越靠近跨中弯矩越小,在跨中处达到最小值。
2.3.2 成桥状态下纵向弯矩的横向分配为进一步对比腹板差异性的影响下纵向受力的横向分配情况,分别对3个腹板所在区域的实体单元受力情况进行数据提取及对比分析。
当前在桥梁设计和验算中对于单箱多室箱梁桥的空间受力计算大多采用梁格法,可以安全高效地计算箱梁在空间效应下的各种受力情况。为了减小计算量同时考虑尽量避免后续施加预应力时产生不必要的分配误差,一般情况下会采用基于腹板位置的划分方式。
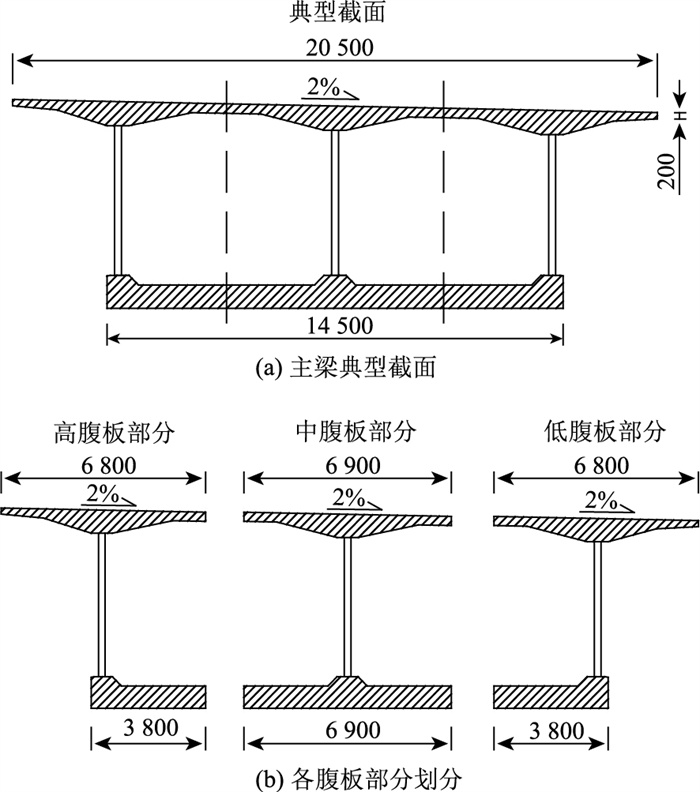
本研究虽为全桥实体建模,并不涉及梁格法,但亦可参照梁格法的思路。在有限元全桥实体模型中将此单箱双室箱梁横向截面视为3部分,即高腹板部分、中腹板部分及低腹板部分(见图 4),使得本研究结果从实体单元建模的角度为梁格法提供一定程度的参考与修正。
|
| 图 4 横截面划分示意图(单位:mm) Fig. 4 Schematic diagrams of cross section division (unit: mm) |
| |
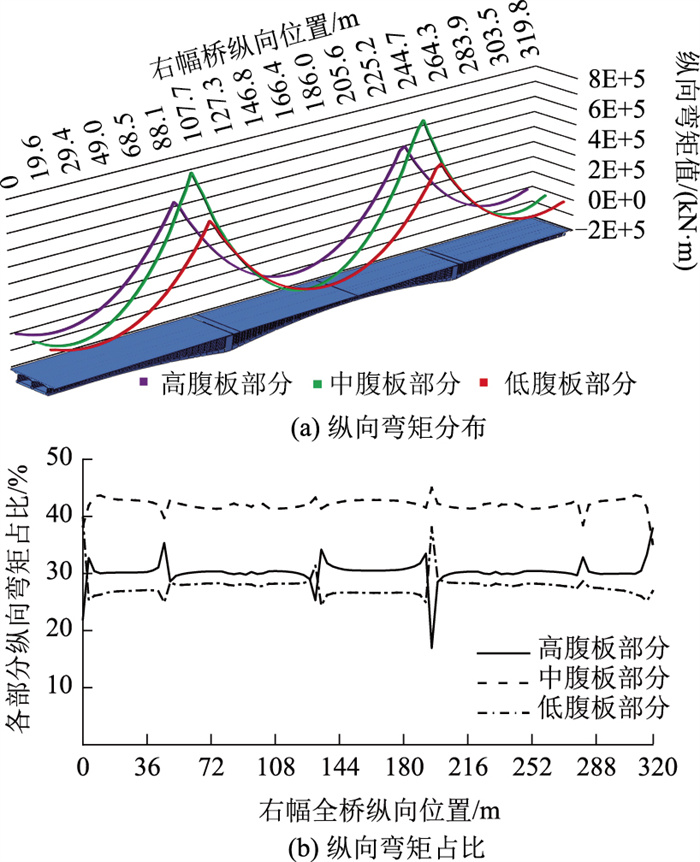
在ABAQUS有限元软件中(见图 4)分别提取出恒载作用下全桥实体模型中3部分区域单元的力学分析结果,分别得到3部分的纵向弯矩的分布情况及各自弯矩值占全截面总弯矩值的比例,如图 5所示。
|
| 图 5 各部分纵向弯矩分布 Fig. 5 Longitudinal bending moment distribution of each part |
| |
由图 5可见,3部分区域的纵向弯矩分布规律与全截面总纵向保持一致。高腹板部分、中腹板部分、低腹板部分的占比范围分别为17%~38%,35%~45%,24%~40%,大都在30%,42%,28%左右浮动。最终呈现规律为:受腹板差异性的影响,成桥状态下的单箱双室波形钢腹板箱梁,其纵向弯矩在横向截面的分配情况为中腹板部分最多,其次为高腹板部分,低腹板部分最少。
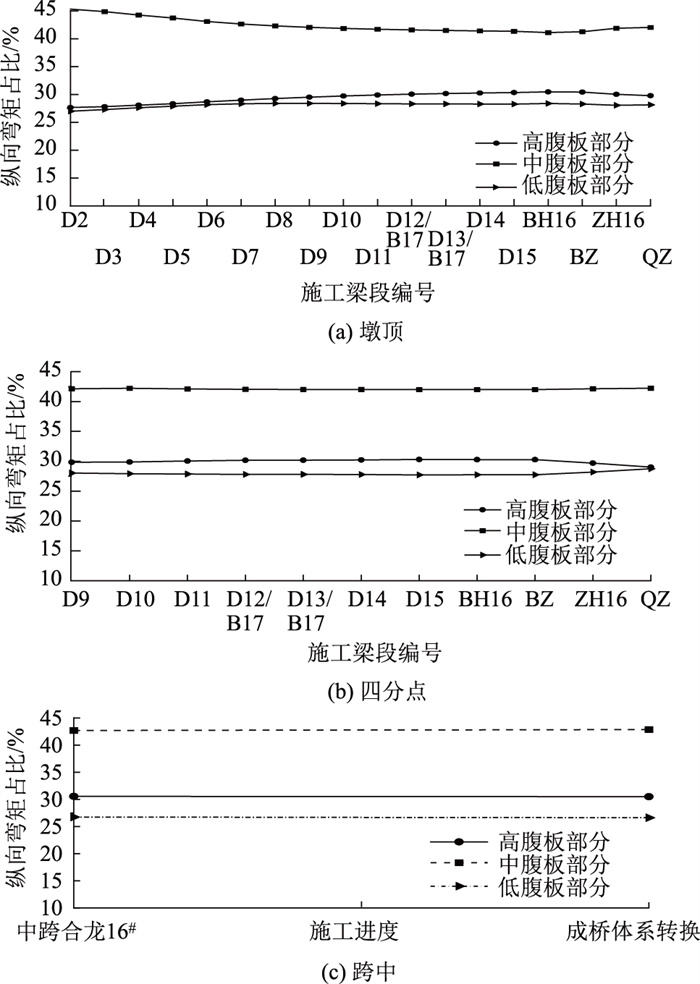
2.3.3 施工状态下纵向弯矩的横向分配为研究施工状态下纵向弯矩的分配情况,在有限元软件中采用生死单元法模拟施工全过程,并取3个特殊位置,即跨中、四分点和墩顶。对比其从双悬臂阶段到单悬臂阶段再到成桥阶段的纵向受力的横向分布比例,得到纵向弯矩横向分配随施工进度的变化情况,如图 6所示。图中BZ为边跨体系转换,QZ为全桥体系转换。
|
| 图 6 典型截面纵向弯矩分配变化 Fig. 6 Variation of longitudinal bending moment distribution for typical sections |
| |
将图 6中的占比变化情况进行总结归纳,得到各典型截面随着施工的不断发展,其纵向弯矩横向分配的最终趋势,如表 4所示。输出从施工到成桥全过程的比例变化情况,得到各典型截面的高腹板部分、中腹板部分、低腹板部分纵向弯矩占比的最大值,如表 5所示。
| 位置 | 双悬臂阶段 | 单悬臂阶段 | 成桥阶段 | ||||||||
| 高腹板 | 中腹板 | 低腹板 | 高腹板 | 中腹板 | 低腹板 | 高腹板 | 中腹板 | 低腹板 | |||
| 跨中 | — | — | — | — | — | — | 30 | 43 | 27 | ||
| 四分点 | 30 | 42 | 28 | 30 | 42 | 28 | 30 | 42 | 28 | ||
| 墩顶 | 30 | 42 | 28 | 30 | 42 | 28 | 30 | 42 | 28 | ||
| 位置 | 双悬臂阶段 | 单悬臂阶段 | 成桥阶段 | ||||||||
| 高腹板 | 中腹板 | 低腹板 | 高腹板 | 中腹板 | 低腹板 | 高腹板 | 中腹板 | 低腹板 | |||
| 跨中 | — | — | — | — | — | — | 31 | 43 | 27 | ||
| 四分点 | 30 | 42 | 28 | 30 | 42 | 28 | 30 | 42 | 28 | ||
| 墩顶 | 30 | 45 | 28 | 31 | 42 | 28 | 30 | 42 | 28 | ||
随着施工进度的不断发展,可发现中腹板部分始终占有最大的比例,高腹板部分与低腹板占比较小,高腹板部分始终大于低腹板部分,二者相差大多处于2%左右。同时可见在动态的施工过程中,3个典型截面的3个腹板部分的占比同成桥状态下全桥横向截面一致,都围绕在30%,42%,28%左右。根据其最终趋势,高腹板部分和低腹板部分占比区别不是很大,但在施工的动态变化过程中,应寻求各部分占比的最大值,用以偏安全地进行施工过程的内力控制计算。因此需要参照表 5中的各部分最大的占比情况,用于偏安全地考量内力情况,并为此类桥梁的设计建造提供一个重要参考。
通过纵向弯矩的横向分配情况不难发现,不论是在成桥状态还是施工的动态变化过程,3个腹板部分的占比情况表现出较为一致的规律,即中间腹板占比较大,其次是高腹板,再其次是低腹板。以上研究均参考了梁格法中通常采用的基于腹板的划分方式,研究结果从实体建模的角度为梁格法提供了相应的修正。在采用不等高腹板的单箱双室波形钢腹板箱梁桥的设计、计算及施工、成桥的动态过程中可以更加偏地安全进行考量。
此外,为探究波形钢腹板箱梁桥纵向弯矩及腹板剪力分配规律是否适用于同类断面箱梁,本研究另建实体模型,将波形钢腹板更换为混凝土腹板,其余条件与上述模型保持一致,采用同样的方式进行了对比分析,如图 7所示。

|
| 图 7 混凝土箱梁纵向弯矩分配 Fig. 7 Longitudinal bending moment distribution of concrete box girder |
| |
以四分点典型截面为例,通过对比可见,混凝土箱梁中纵向弯矩分配亦表现出中间腹板占比最大,其次是高腹板部分,低腹板部分占比最小的规律,然而图 6所示的波形钢腹板箱梁中高腹板与低腹板的弯矩占比差异性更小。这是由于在波形钢腹板箱梁中高腹板部分和低腹板部分混凝土面积类似,混凝土主要用于抗弯,波形钢腹板主要用于抗剪,腹板的差异性对纵向弯矩的分配情况影响较小。而在混凝土箱梁的中腹板部分纵向弯矩占比较波形钢腹板箱梁更小。这是因为波形钢腹板箱梁的中腹板部分的混凝土面积占全截面混凝土的比例更大,而混凝土主要用于抗弯,所以此部分弯矩占比更大。而混凝土箱梁由于所有腹板均为混凝土,中腹板部分的混凝土面积占全截面混凝土面积比例更小,因此弯矩占比更小。
综上,相比混凝土箱梁,波形钢腹板箱梁由于中腹板部分顶底板混凝土占全截面混凝土比例大,纵向弯矩占比更大;而由于波形钢腹板主要用于抗剪,高腹板及低腹板部分弯矩占比相差更小,纵向弯矩的分配受腹板差异性影响更小。
2.3.4 施工状态下腹板的剪力分配上述研究明确了腹板的差异性影响了单箱双室波形钢腹板箱梁纵向弯矩的横向分配,但同时也必须考虑客观情况:中间腹板部分的混凝土区域面积较大,且高腹板部分和低腹板部分纵向弯矩的横向分配比例在2%的差值区间。
为更清晰地探究不同腹板间的受力差别,本研究单独对腹板进行了研究。为充分考虑施工过程中波形钢腹板剪力随施工步骤的动态变化情况,利用ABAQUS软件中的生死单元法计算出四分点截面处3个腹板在施工发展过程中对应的剪力,并得到其剪力占比情况,如图 8所示。

|
| 图 8 波形钢腹板桥腹板剪力分配情况 Fig. 8 Web shear force distribution of corrugated steel web bridge |
| |
由图 8可见,在自重作用下,中腹板的剪力在三者中占有比例最高,其次是高腹板,剪力占比最少的是低腹板。这一点与纵向弯矩的横向分配规律保持一致,高腹板和低腹板相差亦在2%左右。这说明不论是纵向弯矩分配还是剪力的分配,在施工及成桥的动态过程中,均表现出中腹板部分受力占比最大,其次是高腹板部分,最后是低腹板部分。中腹板部分的占比相较其他2个部分,差值较大,而高腹板部分和低腹板部分相差仅在2%左右。
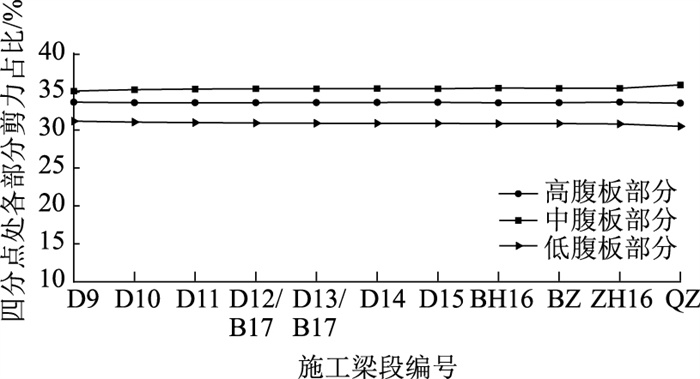
在同类断面混凝土箱梁中,各腹板剪力分配情况如图 9所示。混凝土箱梁中各腹板剪力分配亦表现出中间腹板占比最大,其次是高腹板部分,低腹板部分占比最小的规律,但各部分差异较小。通过与图 8对比,可以明显发现波形钢腹板箱梁中各腹板剪力差异更为显著,并且波形钢腹板占比情况与施工过程相关性更高,表现出明显的变化趋势:刚建成的腹板,其剪力占比情况随后续施工进程逐渐趋于稳定,而混凝土箱梁的腹板剪力分配随施工进度的变化趋势并不明显。这是由于在波形钢腹板箱梁中腹板主要用于抗剪,剪力分配敏感度更高,受波形钢腹板差异性影响更为显著,且更易受到施工进度的影响。
|
| 图 9 箱梁桥腹板剪力分配情况 Fig. 9 Web shear force distributions of box girder bridge |
| |
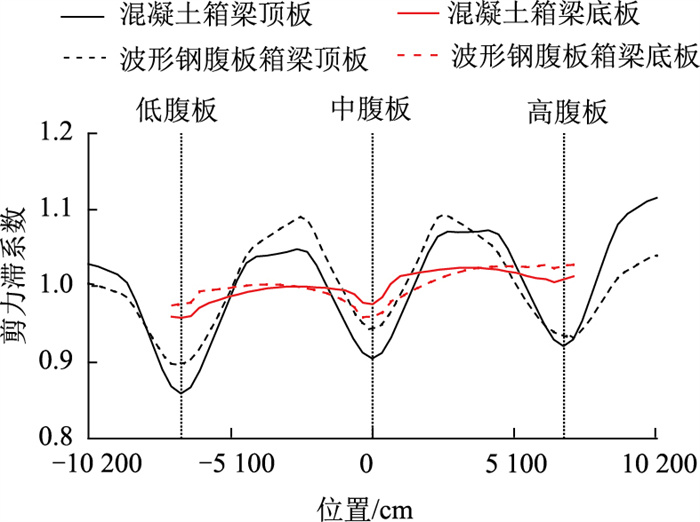
2种箱梁的剪力滞效应状况如图 10所示。由图可见,2种不同的箱梁,其跨中顶板及底板均呈现负剪力滞效应。顶板剪力滞效应较底板更为显著。对于顶板而言,混凝土箱梁剪力滞效应大于波形钢腹板箱梁,最显著处位于低腹板,剪力滞系数分别为0.858和0.896;对于底板而言,在低腹板及高腹板处混凝土箱梁剪力滞效应大于波形钢腹板箱梁,在中腹板处则相反,最显著处位于中腹板,剪力滞系数分别为0.95和0.97。
|
| 图 10 两种箱梁剪力滞系数分布 Fig. 10 Shear lag coefficients distributions for 2 types of box girders |
| |
综上,顶板剪力滞效应较底板更为显著,采用波形钢腹板代替混凝土腹板可以降低箱梁的剪力滞效应。
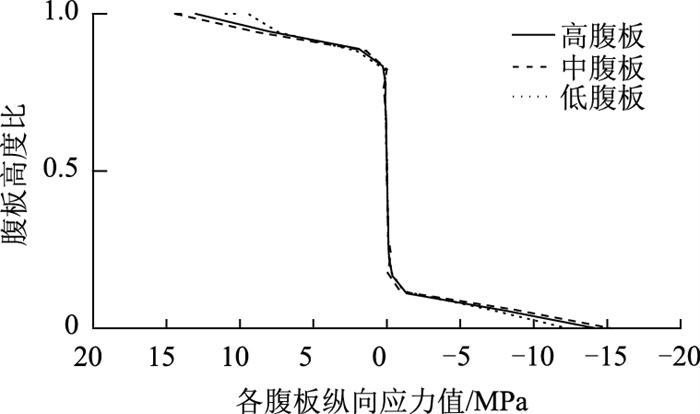
2.3.5 施工状态下腹板纵向应力分配在波形钢腹板组合箱梁桥中,波形钢板的褶皱效应削弱了各腹板的轴向刚度,取全桥模型四分点处截面各腹板的纵向应力值,其纵向应力沿腹板高度的分布情况如图 11所示。
|
| 图 11 纵向应力沿波形钢腹板高度分布情况 Fig. 11 Longitudinal stress distribution along corrugated steel web height |
| |
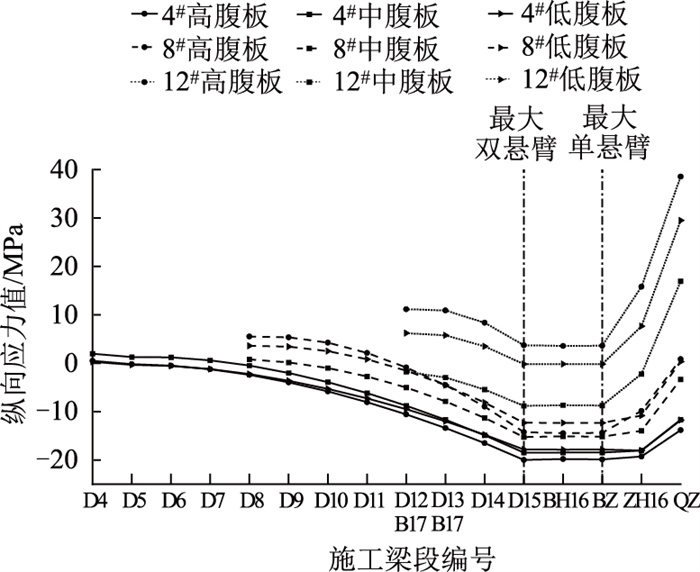
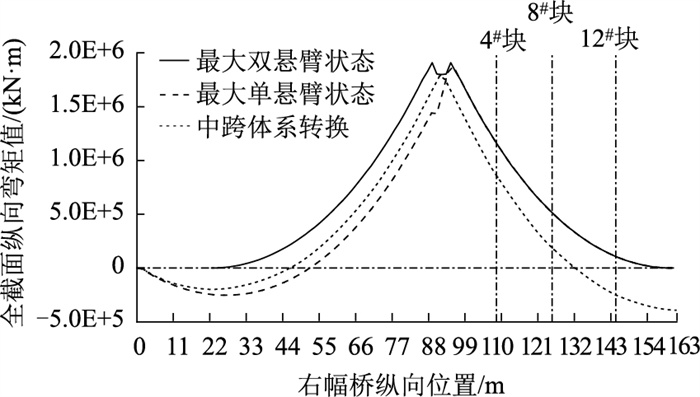
由图 11可见,腹板中间部分纵向应力值接近0 MPa,纵向应力承担能力较差;而越靠近顶底板与腹板的连接位置,各腹板的纵向应力越大,这是由于顶、底板混凝土的影响。钢-混结合段的混凝土对周围的腹板也有相应的影响。为明确施工动态变化过程中腹板纵向应力的分配情况及钢-混结合段的影响,在右幅全桥模型靠近跨中的区域内取4#,8#,12#作为研究对象,得到各节段中心截面内腹板靠近底板连接处的纵向应力,各应力值随施工进度的变化情况如图 12所示。同时输出3种典型施工状态下截面纵向弯矩沿右幅桥梁纵向分布状况,如图 13所示。
|
| 图 12 各腹板纵向应力随施工状态变化 Fig. 12 Longitudinal stress of each web varying with construction states |
| |
|
| 图 13 典型施工状态下纵向弯矩分布 Fig. 13 Longitudinal bending moment distribution in typical construction states |
| |
由图 12和图 13可见,在双悬臂施工期间,各截面下缘所受压应力增大,3个号块各腹板纵向应力值逐渐减小。从最大双悬臂状态过渡到最大单悬臂状态时,靠近跨中部分的区域内全截面的纵向弯矩及腹板纵向应力均无明显变化。而随着中跨合龙及体系转换,各截面下缘所受拉应力增大,因此3个号块各腹板纵向应力值亦增大。
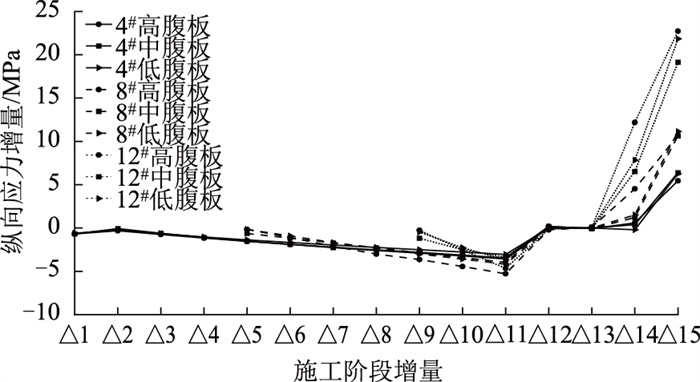
为准确清晰地探究高、中、低3个腹板随施工过程的纵向应力分配状况,求出3个号块各腹板在每个施工阶段较前一阶段的纵向应力增量值,如图 14所示。图中△1~△15分别为从4#块施工至成桥过程中每个施工阶段较前一阶段的纵向应力增量值。
|
| 图 14 各腹板纵向应力增量变化 Fig. 14 Longitudinal stress increment variation of each web |
| |
由图 14可见,从双悬臂阶段过渡到单悬臂阶段再到中跨合龙及体系转换的动态施工过程中,在各腹板纵向应力负值增大阶段及纵向应力正值增大阶段,4#大致表现出:中腹板增量最大,其次是高腹板,最后是低腹板。这是由于钢-混结合段内中腹板处混凝土面积较其他2个腹板更大,越靠近钢-混结合段的节段,其中腹板纵向应力增量越大,因此4#的中腹板增量均大于高腹板和低腹板。而越远离钢-混结合段,如靠近跨中的8#~12#,更加清晰地呈现出纵向应力增量随施工发展的分配规律,即高腹板增量最大,其次是低腹板,最后是中腹板。
3 腹板纵向应力分配实桥试验基于项目依托的在建桥梁进行实桥试验,通过对比有限元分析结果及实桥测试数据,验证本研究理论分析结果的准确性,以波形钢腹板纵向应力分配规律为例,本研究给出其实桥试验方法及测试结果的对比分析情况。
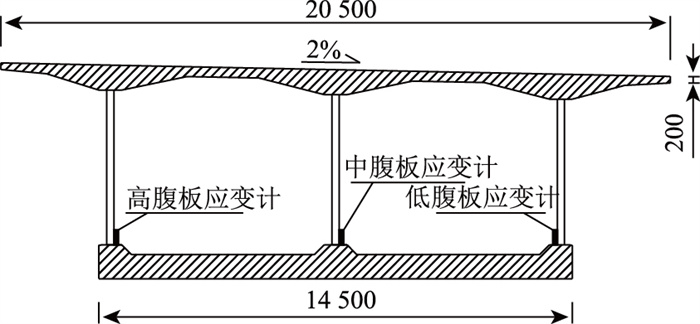
3.1 试验工况采用JMZX-212HAT表面型智能弦式应变计及JMZX-3001综合测试仪对右幅4#的3个腹板下缘位置进行纵向应变的测量,最后通过计算得到纵向应力值,测点位置如图 15所示。
|
| 图 15 测点布置图(单位:mm) Fig. 15 Layout of measuring positions(unit: mm) |
| |
为方便测量,在实际测量时将应变计焊接在波形钢腹板与底板上缘连接的钢板区域中心处,施工范围为:14#浇注完成至边跨合龙16#整体浇筑完成。
3.2 实桥试验结果分析本研究针对右幅4#各腹板在施工范围内的纵向应变进行测量,并通过计算和整理得到各腹板随着施工发展的纵向应力增量,其实测数据如表 6所示。同时通过有限元计算结果进行对比分析,如图 16所示。
| 位置 | 施工阶段增量 | |
| Δ11 | Δ12 | |
| 高腹板 | -4.20 | 1.91 |
| 中腹板 | -5.32 | 3.15 |
| 低腹板 | -4.09 | -0.36 |
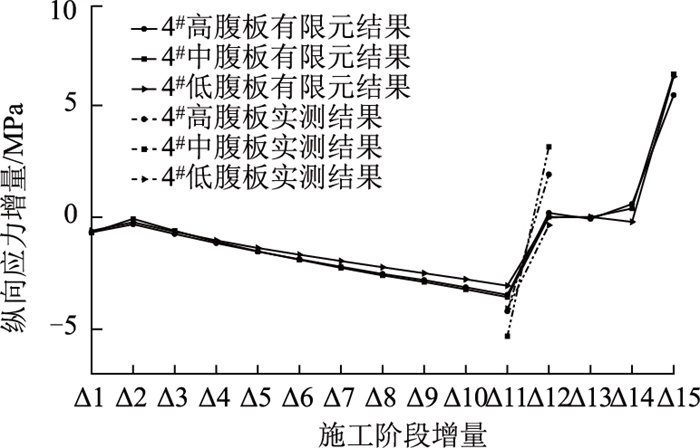
|
| 图 16 实测数据与有限元计算结果对比 Fig. 16 Measured data v.s. finite element calculation result |
| |
由图 16可见,在实际桥梁的施工建造过程中受许多外在因素如温度、桥上人员机械活载等影响,实桥测试结果与有限元分析结果有不同程度的差异。但观察其变化规律不难发现,不论是实桥试验结果还是有限元分析结果,都得到了较为一致的结论:由于右幅4#受到钢-混结合段、腹板高度及位置等因素的影响,在全桥施工的动态过程中,各波形钢腹板纵向正应力及负应力的增量呈现出中腹板最大,其次是高腹板,最后是低腹板的分配规律。
4 结论本研究依托于实际工程,对采用调整腹板高度的方式来设置横坡的单箱双室波形钢腹板箱梁桥进行研究,运用有限元分析方法来探究从施工到成桥的全过程中腹板差异性对其受力分配的影响。
(1) 腹板的差异性对波形钢腹板箱梁的受力分配的确具有一定影响,在设计和计算的过程中应该偏安全地进行考虑。
(2) 本研究参照梁格法中常用的基于腹板的划分方式将截面视为高、中、低3个腹板部分,不论是施工还是成桥状态下,纵向弯矩的横向分配呈现出中间腹板部分占比最大,其次是高腹板部分,低腹板部分最小。各腹板的剪力分配亦表现出同样的规律。
(3) 相比于同类断面混凝土箱梁,波形钢腹板箱梁中纵向弯矩的横向分配受腹板差异性影响更小,但腹板剪力分配及受腹板差异性影响更显著。
(4) 箱梁中顶板剪力滞效应较底板更为显著,采用波形钢腹板代替混凝土腹板可以降低箱梁的剪力滞效应。
(5) 通过有限元结果分析及实桥验证,发现在施工的动态变化过程中钢-混结合段的混凝土影响了附近腹板的纵向应力增量变化规律,使得中腹板的增量大于边腹板,而越远离钢-混结合段,腹板纵向应力增量越清晰地呈现出高腹板增量最大,其次是低腹板,最后是中腹板。
(6) 本研究依托一座典型单箱双室波形钢腹板箱梁桥,采用不等高腹板来实现横向2%坡度时,对应的各施工状态下纵向弯矩偏安全的最大横向分配比例、截面剪力分配及腹板纵向应力分配情况,为相同结构桥梁施工和成桥状态下的安全监控及动态考量提供重要参考。
| [1] |
朱奇挺. 波形钢腹板箱梁腹板剪切屈曲及抗剪承载力研究[D]. 重庆: 重庆交通大学, 2018. ZHU Qiting. Study on shear buckling and shear capacity of corrugated steel web box girder web[D]. Chongqing: Chongqing Jiaotong University, 2018. |
| [2] |
陈今东. 波形钢腹板组合梁桥抗剪及施工技术研究[D]. 长沙: 湖南大学, 2019. CHEN Jindong. Study on shear strength and construction technology of composite girder bridge with corrugated steel webs[D]. Changsha: Hunan University, 2019. |
| [3] |
吕纬, 王捷江. 波形钢腹板箱梁的抗剪性能研究[J]. 建筑技术开发, 2017, 44(4): 97-98. LÜ Wei, WANG Jiejiang. Study on shear behavior of box girder with corrugated steel webs[J]. Building Technology Development, 2017, 44(4): 97-98. |
| [4] |
王超. 变截面波形钢腹板组合梁桥剪切性能试验研究[D]. 南京: 东南大学, 2016. WANG Chao. Experimental study on shear behaviors of girder bridge with variable cross-section and corrugated steel webs[D]. Nanjing: Southeast University, 2016. |
| [5] |
贾慧娟. 变截面波形钢腹板PC组合箱梁桥结构性能研究[D]. 南京: 东南大学, 2015. JIA Huijuan. Research on structural properties of the variable cross-sectional PC composite box-girder bridge with corrugated steel webs[D]. Nanjing: Southeast University, 2015. |
| [6] |
曹海洋. 变高度波形钢腹板组合箱梁的抗剪性能研究[D]. 重庆: 重庆交通大学, 2019. CAO Haiyang. Study on shear behavior of composite box girder with variable height corrugated steel webs[D]. Chongqing: Chongqing Jiaotong University, 2019. |
| [7] |
董旭. 大跨波形钢腹板箱梁桥波形钢腹板及内衬混凝土抗剪性能研究[D]. 济南: 山东大学, 2018. DONG Xu. Research on shear resistance of corrugated steel webs and encased concrete of long span box girder with corrugated steel webs[D]. Jinan: Shandong University, 2018. |
| [8] |
DENG H, SHAO Y B, HASSANEIN M F. Experimental shear testing of small-scale corrugated web girders used in conventional buildings[J/OL]. Journal of Constructional Steel Research, 2022, 189: 107086. https://doi.org/10.1016/j.jcsr.2021.107086.
|
| [9] |
VARGHESE H, KAVITHA P E. Study on strengthening of deteriorated corrugated steel beams using post tensioning[C]// Proceedings of SECON '21. Berlin: Springer, 2022: 419-428.
|
| [10] |
李祖硕. 波形钢腹板连续组合箱梁承载能力试验研究[D]. 北京: 北京交通大学, 2017. LI Zushuo. Experimental study on bearing capacity of continuous composite box girder with corrugated steel webs[D]. Beijing: Beijing Jiaotong University, 2017. |
| [11] |
刘丁实. 波形钢腹板PC组合梁桥的荷载试验研究[D]. 成都: 西南交通大学, 2017. LIU Dingshi. Load test of PC composite beam bridge with corrugated steel webs[D]. Chengdu: Southwest Jiaotong University, 2017. |
| [12] |
GUO C P, PAPANGELIS J P. Torsion of beams with corrugated webs[C]// Proceedings of 9th International Conference on Advances in Steel Structures. Chicago: American Institution of Steel Construction, 2018.
|
| [13] |
李运生, 李孟彪, 王亚萍, 等. 钢-混凝土波形钢腹板组合梁弯扭性能研究[J]. 河北科技大学学报, 2022, 43(1): 99-109. LI Yunsheng, LI Mengbiao, WANG Yaping, et al. Research on bending-torsional behaviors of steel-concrete composite beam with corrugated steel webs[J]. Journal of Hebei University of Science and Technology, 2022, 43(1): 99-109. |
| [14] |
LUKIN A A, KHOLOPOV I S, ALPATOV V Y, et al. Beams with corrugated web: Calculation peculiarities of bending torsion analysis[J].
Procedia Engineering, 2016, 153: 414-418.
|
| [15] |
冉川. 波形钢腹板组合曲线箱梁弯扭行为研究[D]. 成都: 西南交通大学, 2021. RAN Chuan. The bending and torsion behavior of composite curved box grider bridge with corrugated steel webs[D]. Chengdu: Southwest Jiaotong University, 2021. |
| [16] |
王亚萍. 波形钢腹板组合梁弯扭作用机理研究[D]. 石家庄: 石家庄铁道大学, 2021. WANG Yaping. Research on the mechanism of bending and torsion of composite girders with corrugated steel webs[D]. Shijiazhuang: Shijiazhuang Tiedao University, 2021. |
| [17] |
杨轩宇. 考虑徐变效应的曲线波形钢腹板桥弯扭承载能力研究[D]. 兰州: 兰州交通大学, 2021. YANG Xuanyu. Study on the bending and torsional load capacity of curved folded steel webs bridges considering creep effect[D]. Lanzhou: Lanzhou Jiaotong University, 2021. |
| [18] |
GÓRECKI M, LEDZIEWSKI K. Influence of corrugated web geometry on mechanical properties of Ⅰ-beam: Laboratory tests[J/OL]. Materials, 2021, 15(1): 277. (2021-12-30)[2023-06-01]. https://doi.org/10.3390/ma15010277.
|
| [19] |
MATHUR S, SENTHILPANDIAN M. Static and dynamic analysis of corrugated beam with restrained boundary conditions[C]// Advances in Construction Management: Lecture Notes in Civil Engineering. Singapore: Springer, 2022: 91-107.
|
| [20] |
查上, 邓文琴, 刘朵, 等. 波形钢腹板工字钢-混凝土结合板梁桥设计参数分析[J]. 桥梁建设, 2023, 53(1): 87-93. ZHA Shang, DENG Wenqin, LIU Duo, et al. Analysis of design parameters of composite girder bridge with Ⅰ steel girders, concrete slabs and corrugated steel webs[J]. Bridge Construction, 2023, 53(1): 87-93. |
| [21] |
余双伍. 大跨径波形钢腹板连续刚构桥合理设计参数研究[D]. 重庆: 重庆交通大学, 2017. YU Shuangwu. Research on reasonable design parameters of long-span corrugated steel web continuous rigid frame bridge[D]. Chongqing: Chongqing Jiaotong University, 2017. |
| [22] |
LIU D Y, QI T D. Analysis of parameter sensitivity of construction control of multi span PC continuous beam bridge with corrugated steel webs[C]// IOP Conference Series: Earth and Environmental Science. Bristol: IPO Publishing, 2020, 510: 052094.
|
| [23] |
邓飞凡, 谭云浩, 张子龙, 等. 波形钢腹板节段梁预制施工技术研究[J]. 湖南交通科技, 2021, 47(3): 124-128. DENG Feifan, TAN Yunhao, ZHANG Zilong, et al. Research on precast construction technology of segmental girders with corrugated steel webs[J]. Hunan Communication Science and Technology, 2021, 47(3): 124-128. |
| [24] |
梁铎, 王小龙, 章小雨, 等. 顶底板错位施工的波形钢腹板桥梁施工监控技术研究[J]. 公路, 2022, 67(3): 138-142. LIANG Duo, WANG Xiaolong, ZHANG Xiaoyu, et al. Research on the construction monitoring technology of bridges with corrugated steel webs constructed by dislocation of top and bottom slabs[J]. Highway, 2022, 67(3): 138-142. |
| [25] |
祝丰平, 金光雷, 邓文琴, 等. 大跨径波形钢腹板组合梁桥异步施工技术研究[J]. 现代交通技术, 2022, 19(2): 55-59, 92. ZHU Fengping, JIN Guanglei, DENG Wenqin, et al. Study on asynchronous construction technology for long span composite girder bridge with corrugated steel webs[J]. Modern Transportation Technology, 2022, 19(2): 55-59, 92. |
| [26] |
宋胜录. 高墩大跨度波形钢腹板PC组合梁桥施工技术[J]. 建筑施工, 2021, 43(12): 2565-2567. SONG Shenglu. Construction technology of PC composite beam bridge with high pier and large span corrugated steel web[J]. Building Construction, 2021, 43(12): 2565-2567. |
| [27] |
舒宏生, 侯润锋, 刘新华, 等. 波形钢腹板PC组合箱梁桥同步异位悬臂施工新型挂篮设计研究[J]. 施工技术, 2022, 51(5): 57-61. SHU Hongsheng, HOU Runfeng, LIU Xinhua, et al. Design of new hanging basket in synchronous ectopic cantilever construction of prestressed concrete composite box-girder with corrugated steel webs[J]. Construction Technology, 2022, 51(5): 57-61. |
| [28] |
刘旭政, 程坤, 吴刚, 等. 大跨波形钢腹板连续箱梁桥有效分布宽度研究[J]. 公路交通科技, 2022, 39(2): 85-92. LIU Xuzheng, CHENG Kun, WU Gang, et al. Study on effective distribution width of long-span continuous girder bridge with corrugated steel webs[J]. Journal of Highway and Transportation Research and Development, 2022, 39(2): 85-92. DOI:10.3969/j.issn.1002-0268.2022.02.010 |
| [29] |
程坤. 大跨度变截面波形钢腹板组合连续箱梁有效分布宽度研究[D]. 南昌: 华东交通大学, 2017. CHENG Kun. Research on effective distribution width of long span box-girder with corrugated steel webs and various cross-section[D]. Nanchang: East China Jiaotong University, 2017. |
| [30] |
赵品, 荣学亮, 叶见曙. 波形钢腹板组合箱梁横向受力有效分布宽度研究[J]. 湖南大学学报(自然科学版), 2016, 43(7): 105-110. ZHAO Pin, RONG Xueliang, YE Jianshu. Research on the lateral effective width of composite box-girders with corrugated steel webs[J]. Journal of Hunan University (Natural Sciences), 2016, 43(7): 105-110. |
| [31] |
ZHANG Z C, LIU X L, HU Y L, et al. Zig-zag theory for concrete beams with corrugated steel webs[J/OL]. Engineering Structures, 2022, 258: 114100. (2022-05-01)[2023-06-01]. https://doi.org/10.1016/j.engstruct.2022.114100.
|
| [32] |
MOTLAGH H R E, RAHAI A. Long-term behavior of a prestressed concrete bridge with corrugated steel webs[J/OL]. Journal of Bridge Engineering, 2022, 27(1). (2021-11-11)[2023-06-01]. https://doi.org/10.1061/(ASCE)BE.1943-5592.000180.
|
 2025, Vol. 42
2025, Vol. 42



