扩展功能
文章信息
- 夏运达.
- XIA Yunda
- 考虑速度效应和空间间距的双车道元胞自动机模型
- Two-lane cellular automata model considering velocity effect and spacing distance
- 公路交通科技, 2025, 42(7): 13-20
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(7): 13-20
- 10.3969/j.issn.1002-0268.2025.07.002
-
文章历史
- 收稿日期: 2023-08-16
交通流理论研究始于20世纪30年代,研究者用概率论方法统计车流到达规律。二战后,汽车数量增长,车辆跟驰模型、流体力学、气体动理论开始用于车辆相互作用的研究。随着计算机普及,元胞自动机用于交通流理论的研究获得更多关注[1-2]。交通流元胞自动机模型的基础是Nagel[3]于1992年提出的单车道Nagel-Schreckenberg模型,之后又提出双车道Nagel-Schreckenberg模型[4],可模拟出典型交通现象,便于计算机仿真。Barlovic[5]在Nagel-Schreckenberg模型基础上引入慢启动规则,提出VDR(Velocity-Dependent Randomization)模型, 模拟出交通亚稳态。Li[6]引入前车虚拟速度,提出速度效应模型,模拟出的密度-流量峰值更接近交通实测。Knospe[7]引入刹车灯效应,提出舒适驾驶模型,Jiang[8]、Tian[9]对舒适驾驶模型做出改进,使舒适驾驶系列模型模拟驾驶行为更为细化。以上列举较典型的模型,其他模型不再叙述。
元胞自动机的应用推动交通流理论发展,20世纪90年代后期,Kerner[10]提出三相交通流理论(Kerner系列交通流模型大多为元胞自动机模型),即交通状态划分为3个状态:自由流、同步流、宽运动堵塞。交通状态划分为两个状态:自由流和拥挤流,这种理论或模型归结为基本图理论。Kerner[11-12]称,三相交通流理论可以更好描述交通现象和实测数据。但基本图理论支持者[13-14]质疑其支撑数据的准确性。目前,研究者可通过多种工具获得交通实测数据,如线圈探测器、航拍等,但因车辆驾驶员异质性、车辆多样性等因素,即使简单的交通流演化规律仍无法准确获得。Daganzo[15]认为,交通流扰动的演化至今没有实际数据支撑,交通流扰动的成因和增长速度也无法得知。高精度交通测量数据的缺乏导致三相交通流理论和基本图理论存在部分争论。
随着研究深入,三相交通流理论和基本图理论的一些争论已达成共识,比如,均匀拥挤流交通实际不存在。暂未达成共识的一个重要争论点是同步流状态及交通相变问题。三相交通流理论创新性提出同步流状态,同步流的速度介于自由流和宽运动堵塞流之间,并作为独立交通状态存在。三相交通流理论模型为模拟出同步流,模型参数较多,规则较复杂。基本图理论的支持者质疑复杂规则和参数的合理性及同步流的定义。伴随交通相变,三相交通流理论提出,道路系统中随着车流密度增加至临界值,道路上车辆的换道次数会骤减,基本图方法认为不会发生骤减。三相交通流理论研究得出,自由流首先相变为同步流,再相变为宽运动堵塞流。基本图方法认为,自由流可以直接相变为堵塞流,无需同步流这一中间状态过渡。
面对三相交通流理论和基本图理论,研究者建模时,习惯于先归于其中一个理论框架,再设置模型规则及参数,使模型尽可能模拟其理论所对应的交通实测。本研究提出一个新双车道元胞自动机模型,模型规则考虑速度效应和空间间距,模型初始暂不归于其中一个理论框架,不去模拟其中一个理论对应的交通实测,而是通过数值模拟研究两个理论之间暂未达成共识的同步流状态及交通相变问题,探讨两方中较为合理的观点。
1 新双车道模型交通流自身复杂的演化给交通实测带来难度,而有组织的车辆试验可以减少车辆驾驶员异质性、车辆多样性等因素对交通实测的影响。Jiang[16-17]在合肥市组织成规模的车辆跟驰试验。试验车辆安装精度较高的测量设备,以实时记录速度和位置,试验车辆均安排稳重的驾驶员。研究成果表明,某一辆车在前行驶,与随后车辆的间距较小,如果前车速度发生变化,随后车辆倾向于保持现有速度和行驶状态。当该车辆与随后车辆的间距较大,如果前车速度发生变化,后车倾向于改变现有车速和状态,发生跟驰行为。
本研究根据以上成果,提出的新双车道元胞自动机模型规则如下所示。
Rule1: 加速
| $ V_{(i, t+1)}=\min \left\{V_{(i, t)}+1, V_{\max }\right\} 。$ | (1) |
Rule2: 减速
| $ V_{(i, t+1)}=\min \left\{V_{(i, t+1)}, d_{i, t}+V_{(i+1, t+1)}^{\prime}\right\}, $ | (2) |
其中,
| $ \begin{gathered} V_{(i+1, t+1)}^{\prime}=\min \left\{V_{\max }-1, V_{(i+1, t)}, \right. \\ \left.\max \left(0, d_{(i+1, t)}-1\right)\right\} 。\end{gathered} $ |
Rule3: 以概率p随机慢化
| $ V_{(i, t+1)}=\max \left\{V_{(i, t+1)}-1, 0\right\}, $ | (3) |
其中,
| $ p= \begin{cases}p_1 & d_{(i, t)}+V_{(i+1, t+1)}^{\prime} \geqslant d_0 \\ p_2 & d_{(i, t)}+V_{(i+1, t+1)}^{\prime}<d_0\end{cases}。$ |
Rule4: 位置移动
| $ X_{(i, t+1)}=X_{(i, t)}+V_{(i, t+1) }。$ | (4) |
Rule5: 换道动机
| $ \min \left\{V_{(i, t)}+1, V_{\max }\right\}>d_{(i, t)}+V_{(i+1, t+1)}^{\prime}, $ | (5) |
| $ d_{(i, t)}^{\text {front }}>d_{(i, t)}+V_{(i+1, t+1)}^{\prime} 。$ | (6) |
Rule6: 安全条件
| $ d_{(i, t)}^{\text {back }}>d_{\text {safe }}, $ | (7) |
式中,
Rule1和Rule2表示单车道的加减速规则,与引言中的速度效应模型规则一致。合肥试验研究成果的理念体现于Rule3,当前车虚拟速度V(i+1, t+1)′与前车和后车的空间间距d(i, t)的数值和大于等于阈值间距d0,随机慢化概率为p1;当前车虚拟速度V(i+1, t+1)′与前车和后车的空间间距d(i, t)的数值和小于阈值间距d0,随机慢化概率为p2,p1的数值小于p2的数值。新模型考虑速度效应和空间间距,Rule3中前车虚拟速度与空间间距的数值和随机慢化概率相关联,前车的虚拟速度和空间间距影响后车的行驶状态,当空间间距较大时,后车随前车的状态变化做出反应。Rule5,Rule6中前车虚拟速度与空间间距的数值之和与相邻车道空间相关联,当数值之和小于后车与相邻车道前车的空间间距,后车趋向于换道进而达到速度更新目的。双车道系统中,车辆之间相关联,有同步速度的趋势。三相交通流理论模型提出速度适应机制[12],即道路系统中车辆根据间距更新状态,本研究新模型数值模拟近似发生该机制。
数值模拟采用周期边界条件,考虑清晰表达数值模拟结果以及计算机仿真环境,道路长度参数取值为Lroad=1 000 cells,总时间步取值为20 000 s。每个元胞(cell)长度为7.5 m,只容纳一辆车,即每辆车长度7.5 m(引言中列举的典型模型[3-9],其车辆长度均取值为7.5 m)。实际普通汽车的长度区间一般为3~5 m,模型车辆长度取值的7.5 m包含车辆前后的最小反应距离(比如,元胞自动机模型中两辆车的空间间距为0,不代表两辆车直接接触,而是仍保持一定反应距离)。此外,文献[13]提到“飞返效应”,即大型车的超车行为导致交通相变。飞返效应暂未获得普遍认可,本研究新模型不考虑车辆类型影响(引言中列举的典型模型[3-9]均不考虑车辆类型影响)。道路系统中的车辆最大速度取值为Vmax=5 cells/s,与引言中提到的Nagel-Schreckenberg模型、VDR模型、速度效应模型的最大速度一致, 为常见的参数取值。换道安全间距取值为dsafe=5 cells,与最大速度的数值一致,保证车辆换道的空间安全。上文提到,合肥试验研究成果的理念体现于Rule3,保证p1的数值小于p2的数值。经过比对,随机慢化概率取值为p1=0.1,p2=0.5,阈值间距取值为d0=3。
新模型数值模拟用于研究两个理论之间暂未达成共识的同步流状态及交通相变问题。同步流状态的识别方法仍存在争论,目前应用广泛的识别方法主要有时空轨迹图、中断效应和相关函数分析。时空轨迹图是交通状态的重要特征,研究者一般将实测数据绘制成时空轨迹图,或将交通流模型模拟出的数据绘制成时空轨迹图,以判断交通状态及演化。三相交通理论提出“中断效应”来判别同步流状态,即道路系统处于同步流状态时,区别于堵塞状态,道路系统中平均车速低于自由流状态的平均车速,但不会出现成规模的堵塞集团。Neubert[18]通过研究交通实测数据的相关函数,发现道路系统处于同步流状态时,随着时间增长,局部密度、平均速度、流量的自相关函数趋于归零,局部密度和流量的互相关函数也趋于归零。本研究首先应用以上识别方法研究同步流状态,再研究换道次数变化及交通相变等问题,以下为新双车道模型的数值模拟结果。
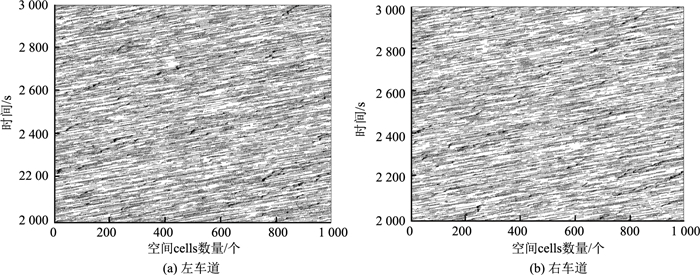
2 数值模拟结果 2.1 时空轨迹图图 1为车流密度ρ=0.1时,新双车道模型的时空轨迹图,黑色点为车辆位置,白色为两车的空间间距(即两黑色点之间的空白元胞数量)。横坐标表示整条车道空间,整条车道为1 000个元胞,对应Lroad=1 000 cells。纵坐标为时间,总时间步为20 000 s,取2 000~3 000 s时间步的车辆空间轨迹为代表。从图 1可以看出,当车流密度ρ=0.1时,黑色点较少,道路系统中车辆数量较少,车辆以高速行驶,道路系统处于自由流状态。
|
| 图 1 道路系统车流密度ρ=0.1时,左、右车道的时空轨迹图 Fig. 1 Spatio-temporal trajectory on left lane and right lane when road system density is 0.1 |
| |
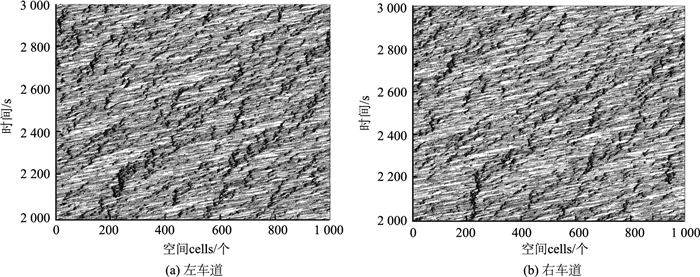
图 2为车流密度ρ=0.2时,新双车道模型的时空轨迹图,取2 000~3 000 s时间步的车辆空间轨迹图为代表。从图 2可以看出,图 2黑色点比图 1多,黑色点的分布较为均匀,道路系统处于自由流向拥挤流过渡的状态。
|
| 图 2 道路系统车流密度ρ=0.2时,左、右车道的时空轨迹 Fig. 2 Spatio-temporal trajectory on left lane and right lane when road system density is 0.2 |
| |
图 3为车流密度ρ=0.4时,新双车道模型的时空轨迹图,取2 000~3 000 s时间步的车辆空间轨迹图为代表。从图 3可以看出,部分黑色点连接成团,表示出现排队现象。此时,道路系统中车辆较多,处于拥挤流状态。

|
| 图 3 道路系统车流密度ρ=0.4时,左、右车道的时空轨迹 Fig. 3 Spatio-temporal trajectory on left lane and right lane when road system density is 0.4 |
| |
图 2与典型三相交通流理论模型模拟出的时空图比较,比如MCD(Modified Comfortable Driving)模型[8],对于本研究双车道模型模拟出的自由流向拥挤流过渡的中间状态,其时空轨迹图为三相交通流理论定义的同步流状态的时空轨迹图。下一节为新双车道模型的速度分布和空间分布,从速度分布和空间分布看道路系统中是否存在成规模的堵塞集团。
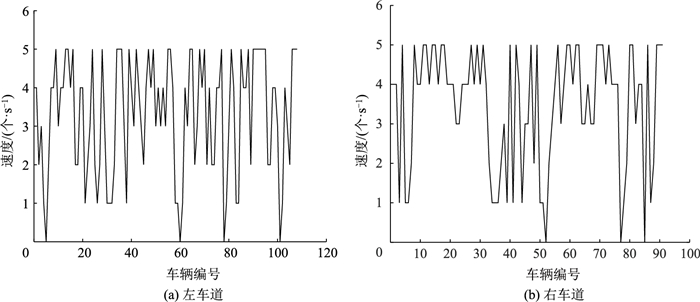
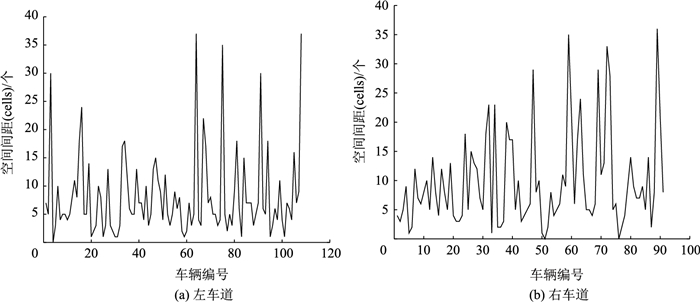
2.2 速度和空间间距对应图 2自由流到拥挤流的中间状态,当道路系统车流密度ρ=0.2时,选取第3 000时间步,观察道路系统中的速度分布和空间间距分布。从图 4(a)中可以看出,第3 000时间步左侧车道有4辆车速度为0。从图 5(a)中可以看出,在第3 000时间步,左侧车道车辆之间的空间间距为0出现1例。从图 4(b)中可以看出,在第3 000时间步,右侧车道有3辆车速度为0。从图 5(b)中可以看出,在第3 000时间步,右侧车道车辆之间的空间间距为0出现2例。从第3 000时间步道路系统中的速度分布和空间间距分布看出,左侧和右侧车道没有出现成规模的堵塞集团。
应用三相交通流理论提出的“中断效应”识别方法,新双车道模型模拟出的自由流到拥挤流的这一中间状态满足同步流状态的定义。下一节为新双车道模型的相关函数分析。
2.3 相关函数分析相关函数分析包括两方面:自相关函数和互相关函数,公式分别如下:
| $ a_x(\tau)=\frac{\langle x(t) x(t+\tau)\rangle-\langle x(t)\rangle^2}{\left\langle x(t)^2\right\rangle-\langle x(t)\rangle^2}, $ | (8) |
| $ c_{x, y}(\tau)=\frac{\langle x(t) y(t+\tau)\rangle-\langle x(t)\rangle\langle y(t)\rangle}{\sqrt{\left\langle x(t)^2\right\rangle-\langle x(t)\rangle^2} \sqrt{\left\langle y(t)^2\right\rangle-\langle y(t)\rangle^2}}, $ | (9) |
式中,ax(τ)为自相关函数;cx, y(τ)为互相关函数,τ为时间;〈 〉为时间序列的平均值。x(t)或y(t)为通过道路系统中虚拟探测器收集固定横断面的流量、局部密度或平均速度的时间序列。
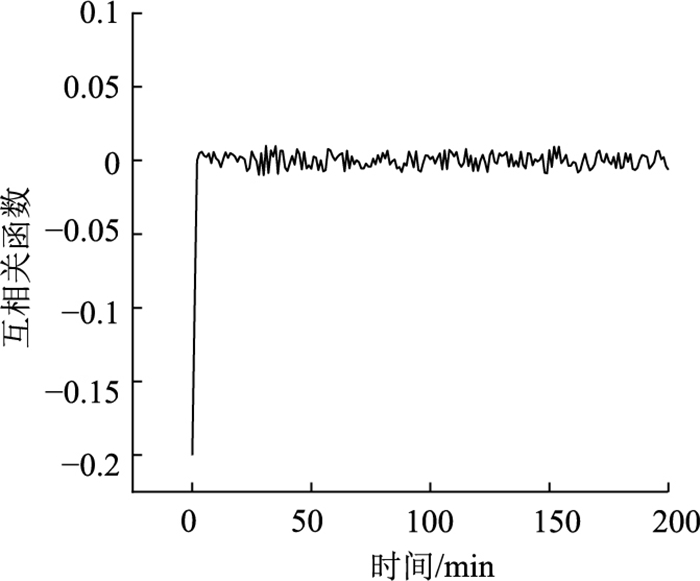
图 6和图 7是当道路系统车流密度ρ=0.2时,新双车道模型的相关函数分析,局部密度、平均速度、流量的自相关函数趋于归零,局部密度和流量的互相关函数也趋于归零。

|
| 图 6 自相关函数分析 Fig. 6 Autocorrelation function analysis |
| |
|
| 图 7 互相关函数分析 Fig. 7 Cross-correlation function analysis |
| |
从相关函数分析可以看出,新双车道模型模拟出的自由流到拥挤流的这一中间状态满足同步流状态的定义。从时空轨迹图、中断效应、相关函数分析综合来看,同步流作为独立交通状态存在,相对于复杂的三相交通流理论模型,新双车道模型以简单规则模拟出同步流状态。
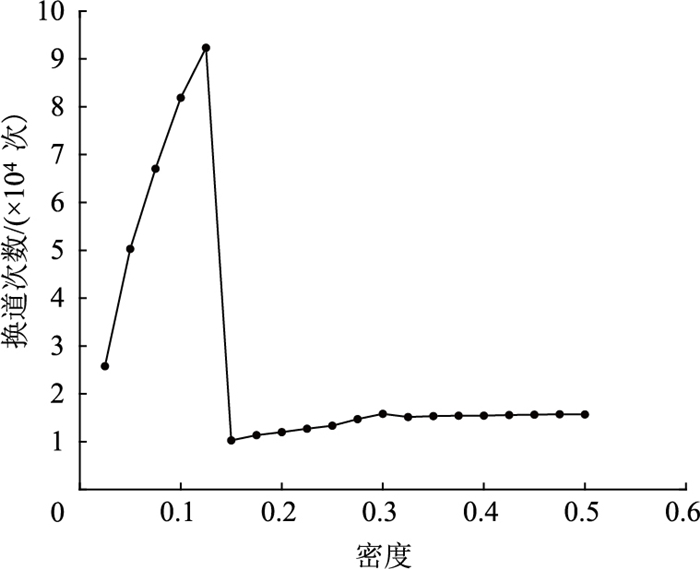
2.4 换道次数变化和交通相变换道次数变化伴随交通状态的改变,换道次数变化与交通相变密切相关。图 8是道路系统中车辆换道次数与密度的关系图,从图 8可以看出,随着道路系统中车流密度增加至临界值,道路系统中车辆的换道次数发生骤减。参见文献[19]提供的换道次数与密度关系曲线,三相交通流理论支持者提供的数据表示,随着道路系统中车流密度增加,道路系统中车辆的换道次数会骤减,呈现“Z”形结构。基本图理论支持者提供的数据表示,随着道路系统中车流密度增加至峰值,再缓慢下降。本研究新双车道模型模拟出的车辆换道次数与密度的关系曲线,以峰值为界,峰值之前,与基本图理论数据一致;峰值之后,与三相交通流理论数据一致。
|
| 图 8 道路系统中换道次数与密度的关系曲线 Fig. 8 Relation curve between lane-changing frequency and density in road system |
| |
新模型Rule5,Rule6为换道规则,前车与后车的空间间距不能满足后车的速度更新,相邻车道前车与本车道后车的空间间距能够满足后车的速度更新,后车发生换道行驶行为。在理想的换道规则下,随着道路系统中的车流密度增加,车辆的数量增加,换道次数随之增加。实际处于高速运行的车流,车流密度较小时,车辆换道不只是受到相邻车道空间间距的影响,道路线型或环境等因素对换道次数影响较大。所以本研究认为换道次数峰值前,车流密度较小时,换道次数变化无明显规律性,三相交通流理论和基本图理论提供的数据都可能发生,图 8中峰值前的换道次数变化仅为理想条件下。当车流密度增加至临界值,道路系统中车辆数量随之增加,换道次数达到峰值后,此时相邻车道的整体空间条件变差,车辆换道动机骤减,换道次数随之发生骤减。本研究关于换道次数变化的研究仅是理论分析,最终解决这一争论的关键仍是高精度交通实测。
三相交通流理论和基本图理论关于交通相变的争论仍是关注于同步流,三相交通流理论认为自由流到堵塞流需经过同步流的过渡,基本图理论认为自由流可直接相变为堵塞流。本研究笔者在文献[20]提出一个考虑速度差和减速幅度的单车道模型,以探讨交通相变,研究认为,当道路系统中出现大量倾向于急减速的车辆,自由流在此条件下可直接相变为堵塞流,支持基本图理论的观点。文献[20]与本研究为一整体,考虑篇幅因素,不在此详细叙述。
3 结论本研究提出一个考虑速度效应和空间间距的双车道元胞自动机模型,探讨三相交通流理论和基本图理论之间争论的同步流状态和交通相变问题。从时空轨迹图、中断效应、相关函数分析看出,同步流作为独立交通状态存在,支持三相交通流理论的观点,相对于复杂的三相交通流理论模型,新双车道模型以简单规则模拟出同步流状态。分析新双车道模型模拟的车辆换道次数与密度的关系曲线后认为,随着密度增长,换道次数峰值前,换道次数变化无明显规律性,两个理论的观点都有可能发生。密度增长至临界值,双车道系统的车辆换道次数达到峰值后,换道次数发生骤减,支持三相交通流理论的观点。自由流在一定条件下可直接相变为堵塞流,支持基本图理论的观点。
随着交通实测精度的提高,如均匀拥挤流交通不存在、道路通行能力具有概率特性等三相交通理论与基本图理论之间的争论点已逐渐达成共识[21],其他争论点的最终达成共识仍是未来研究的重点。
| [1] |
张建旭, 胡帅, 金宏意. 人机混驾交通流事故预警换道决策及特性分析[J]. 公路交通科技, 2023, 40(11): 212-221, 236. ZHANG Jianxu, HU Shuai, JIN Hongyi. Lane-changing decision and characteristic analysis on accident warning of mixed traffic flow with human-driving and autonomous vehicle[J]. Journal of Highway and Transportation Research and Development, 2023, 40(11): 212-221, 236. |
| [2] |
车松珊, 钱勇生, 曾俊伟, 等. 基于驾驶人有限理性的交织区换道行为决策[J]. 公路交通科技, 2023, 40(9): 166-174. CHE Songshan, QIAN Yongsheng, ZENG Junwei, et al. Lane-changing behavior decision in weaving area based on drivers' bounded rationality[J]. Journal of Highway and Transportation Research and Development, 2023, 40(9): 166-174. |
| [3] |
NAGEL K, SCHRECKENBERG M. A cellular automaton model for freeway traffic[J].
Journal de Physique Ⅰ, 1992, 2(12): 2221-2229.
|
| [4] |
NAGEL K, WOLF D E, WAGNER P, et al. Two-lane traffic rules for cellular automata: A systematic approach[J].
Physical Review E, 1998(58): 1425-1437.
|
| [5] |
BARLOVIC R, SANTEN L, SCHADS-CHNEIDER A, et al. Metastable states in cellular automata for traffic flow[J].
The European Physical Journal B-Condensed Matter and Complex Systems, 1998, 5(3): 793-800.
|
| [6] |
LI X B, WU Q S, JIANG R. Cellular automaton model considering the velocity effect of a car on the successive car[J].
Physical Review E, 2001, 64: 066128.
DOI:10.1103/PhysRevE.64.066128 |
| [7] |
KNOSPE W, SANTEN L, SCHADS-CHNEIDER A, et al. Towards a realistic microscopic description of highway traffic[J].
Journal of Physics A: Mathematical and General, 2000, 33(48): 477-485.
|
| [8] |
JIANG R, WU Q S. Cellular automata models for synchronized traffic flow[J].
Journal of Physics A: Mathematical and General, 2003, 36(2): 381-390.
|
| [9] |
TIAN J F, JIA N, ZHU N, et al. Brake light cellular automaton model with advanced randomization for traffic breakdown[J].
Transportation Research Part C, 2014, 44: 282-298.
|
| [10] |
KERNER B S. Experimental features of self-organization in traffic flow[J].
Physical Review Letters, 1998, 81(17): 3797-3800.
|
| [11] |
KERNER B S, KLENOV S L, SCHREC-KENBERG M. Simple cellular automaton model for traffic breakdown, highway capacity, and synchronized flow[J].
Physical Review E, 2011, 84(2): 046110.
DOI:10.1103/PhysRevE.84.046110 |
| [12] |
KERNER B S. Criticism of generally accepted fundamentals and methodologies of traffic and transportation theory: A brief review[J].
Physica A, 2013, 392(21): 5261-5282.
|
| [13] |
SCHÖNHOF M, HELBING D. Criticism of three-phase traffic theory[J].
Transportation Research Part B, 2009, 43(7): 784-797.
|
| [14] |
TREIBER M, KESTING A, HELBING D. Three-phase traffic theory and two-phase models with a fundamental diagram in the light of empirical stylized facts[J].
Transportation Research Part B, 2010, 44(8/9): 983-1000.
|
| [15] |
DAGANZO C F, CASSIDY M J, BERTINI R L. Possible explanations of phase transitions in highway traffic[J].
Transportation Research Part A: Policy and Practice, 1999, 33(5): 365-379.
|
| [16] |
JIANG R, HU M B, ZHANG H M, et al. Traffic experiment reveals the nature of car-following[J/OL]. PloS ONE, 2014, 9(4): e94351(2014-04-16)[2025-01-21]. https://doi.org.10.1371/journal.pone.0094351.
|
| [17] |
JIANG R, HU M B, ZHANG H M, et al. On some experimental features of car-foll-owing behavior and how to model them[J].
Transportation Research Part B, 2015, 80: 338-354.
|
| [18] |
NEUBERT L, SANTEN L, SCHADS-CHNEIDER A, et al. Single-vehicle data of highway traffic: A statistical analysis[J].
Physical Review E, 1999, 60(6): 6480-6490.
|
| [19] |
田钧方. 基于基本图和三相交通流理论的离散建模方法研究[D]. 北京: 北京交通大学, 2013. TIAN Junfang. Research on the discrete modeling method within the fundamental diagram approach and three phase traffic flow theory[D]. Beijing: Beijing Jiaotong University, 2013. |
| [20] |
夏运达, 赵杨. 考虑前后车速度和减速幅度的元胞自动机模型[J]. 交通运输系统工程与信息, 2019, 19(2): 73-79. XIA Yunda, ZHAO Yang. Cellular automaton model considering velocity of the front and rear vehicles and deceleration values[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(2): 73-79. |
| [21] |
夏运达. 基于元胞自动机模型的道路交通流复杂特性的研究[D]. 长沙: 湖南大学, 2018. XIA Yunda. Research on the complex characteristics of road traffic flow based on cellular automaton models[D]. Changsha: Hunan University, 2018. |
 2025, Vol. 42
2025, Vol. 42