扩展功能
文章信息
- 孙士尧, 周勇军, 王业路, 张恒, 赵煜, 药天运.
- SUN Shiyao, ZHOU Yongjun, WANG Yelu, ZHANG Heng, ZHAO Yu, YAO Tianyun
- 基于目标可靠指标的独柱墩单点支撑梁桥整体倾覆稳定性
- Overall overturning stability of single-column pier single-point supported girder bridge based on target reliability indicator
- 公路交通科技, 2025, 42(7): 121-132
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(7): 121-132
- 10.3969/j.issn.1002-0268.2025.07.013
-
文章历史
- 收稿日期: 2025-02-25
2. 青岛理工大学 土木工程学院,山东 青岛 266033;
3. 长安大学 建筑工程学院,陕西 西安 710061
2. School of Civil Engineering, Qingdao University of Technology, Qingdao, Shandong 266033, China;
3. School of Civil Engineering, Chang 'an University, Xi 'an, Shaanxi 710061, China
近年来因违规超载车辆导致独柱墩梁桥发生倾覆倒塌现象屡有报道[1-3],给社会带来严重的负面影响和经济损失。在偏载车辆作用下,桥梁上部梁体沿轴线产生有约束的扭转变形;随着偏载的增大,远离汽车偏载侧的支座脱空,梁体发生大变形转动;当偏载继续增大直至滑动力大于抗滑力时,桥梁发生倾覆破坏[4-6]。
在公路桥梁汽车荷载标准研究方面,桥梁的横向抗倾覆稳定性与所采用的汽车荷载标准联系密切。现有研究表明桥梁的倾覆破坏多是由超载车辆偏载作用引起,按照标准车道荷载进行独柱墩梁桥的抗倾覆设计无法保证其在实际运营过程中的安全性。因此,浙江省和广东省等先后给出了抗倾覆计算的汽车荷载标准,通过采用55 t密集车队荷载或调整车道系数保证桥梁结构横向稳定的安全冗余度[7-9]。曹景[10]通过分析得出公路Ⅰ级荷载用于抗倾覆稳定性计算偏于不安全,宜采用5 m间距55 t密排重车车队。Wang[11]研究表明在汽车荷载竖向加载总量相同的情况下,55 t汽车车队荷载模型比公路Ⅰ级和AASHTO荷载模型更容易引起桥梁的倾覆破坏。综上可知,桥梁结构的抗倾覆稳定问题不同于结构强度问题,有其自身的特点[12]。汽车荷载具有时变性和随机性,对桥梁的竖向效应(弯矩、剪力)和横向效应(扭矩)影响不同,现有研究成果缺乏桥梁抗倾覆分析的统一汽车荷载标准。
在独柱墩梁桥的抗倾覆稳定性研究方面,国内外学者通常基于确定性分析模型,采用不同的抗倾覆计算方法得到独柱墩梁桥的抗倾覆稳定性系数[10],以判断其抗倾覆稳定性是否满足要求。庄冬利[13]认为在确定抗倾覆稳定系数时,将主梁作为刚体的计算方法是不合理的,应采用弹性体空间计算模型进行抗倾覆分析。彭卫兵[8]结合独柱墩梁桥的典型破坏模式,构造了抗倾覆承载力实用计算方法及简化计算方法。徐亚峰[14]通过多目标优化设计增设钢盖梁的加固方案,显著提升独柱墩直线梁桥的抗倾覆能力并减小偏心弯矩。Deng[15]通过改进静力作用下的抗倾覆分析方法,研究得出在地震作用下若忽略离心力的影响将得到较大的抗倾覆稳定性系数。Zhuang[16]通过横向滑移平衡方程对传统的抗倾覆稳定性系数分析方法进行修正,得到同时考虑倾覆和滑动的分析方法。Peng[17]提出了综合考虑独柱墩梁桥倾覆破坏机理和倾覆临界状态的抗倾覆稳定性综合分析方法。以上研究多采用确定性分析模型,未能充分反映荷载效应的随机性,基于确定性的荷载效应进行抗倾覆稳定性评价可能会高估桥梁结构的安全储备。
早期的安全系数法将结构尺寸、材料性能和荷载等不确定因素当作定值处理,以安全系数表示结构的安全储备,缺乏合理的科学依据。当前工程结构设计已向以概率为基础的极限状态设计法发展,然而准确地考虑各种不确定因素十分困难,为此,学者们[18-19]通过将各种不确定性的参量作为随机变量看待,以其概率分布特征描述各种不确定因素,通过概率分析和计算,得到评价结构安全裕度的指标,即可靠度或失效概率。
综上,独柱墩梁桥的抗倾覆稳定性研究主要存在的问题为:一是《公路桥涵设计通用规范》(JTG D60—2015)中的汽车荷载标准是基于概率统计所得[20-22],而桥梁的倾覆破坏多是由超载车辆偏载作用引起,它与规范的荷载标准并不相同;二是现有研究多采用确定性分析模型,未能充分反映荷载效应的随机性。因此,本研究采用理论分析和数值仿真相结合的方法,同时结合目标可靠指标建立随机性分析模型,提出考虑各荷载效应随机性的抗倾覆稳定性分析方法。
1 抗倾覆稳定性计算方法对比分析为比较不同抗倾覆计算方法的适用性,分别选取2座实际发生倾覆事故的独柱墩梁桥,并采用刚性倾覆轴法、折线倾覆轴法和修正倾覆轴法这3种抗倾覆计算方法[23]进行对比分析。
1.1 桥梁简介及模型建立广东省某高速匝道桥[24-25]上部结构为3×25 m曲线独柱墩梁桥,全桥曲率半径为230.0 m,桥面宽为8.5 m,支座高度为0.2 m。其发生倾覆破坏事故的诱因为4辆超载车辆密集偏载行驶,质量分别为76.4,111.5,102.9,108.9 t。
江苏省某跨线桥[24-25]为(25+35+25)m直线独柱墩梁桥,桥面宽为9.5 m,支座高度为0.2 m。其发生倾覆破坏事故的诱因为2辆超载车辆偏载行驶,质量分别为160.6 t和160.9 t。
采用有限元软件ANSYS19.2建立仿真分析模型,考虑梁体截面的翘曲和畸变,采用SOLID45单元模拟主梁,按照现行规范中的标准车辆荷载形式,将倾覆事故车辆荷载按照实际行驶位置以多个集中力的形式施加于桥面,护栏和桥面铺装质量按实际质量计算后附加到桥梁顶板重度中来共同考虑。由于箱梁在倾覆时未发生强度破坏,梁体完好,故主梁的建立采用弹性模型。
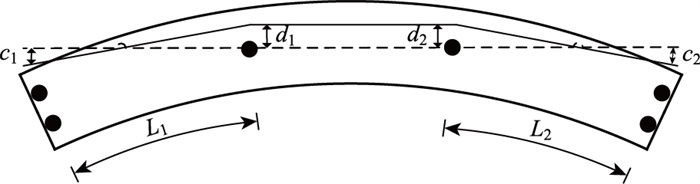
1.2 修正倾覆轴法不同桥型的独柱墩梁桥具有不同的倾覆轴线,以三跨独柱墩梁桥为例,当为曲线桥梁时,修正倾覆轴的位置如图 1所示,位置参数如式(1)和式(2)所示[23]。
| $ c_i=\frac{R L_i}{2000} \times h_{c i} \geqslant 0, $ | (1) |
| $ d_i=0.5 h_{\mathrm{d} i}, $ | (2) |
|
| 图 1 三跨曲线独柱墩梁桥修正倾覆轴示意图 Fig. 1 Schematic diagram of corrected overturning axis of three-span curved single-column pier girder bridge |
| |
式中,ci为第i个联端外侧支座处2个中墩支座连线与修正倾覆轴的间距;R为独柱墩梁桥的曲率半径;Li为第i个联端外侧支座与相邻中墩支座之间的主梁中心线长度;hci为第i个联端外侧支座的有效厚度(取支座高度的0.75倍);di为第i个中墩支座与修正倾覆轴的间距;hdi为第i个中墩支座的有效厚度(取支座高度的0.75倍)。
当为直线桥梁时,修正倾覆轴的位置如图 2所示,位置参数如式(3)和式(4)所示。
| $ c_i=h_{\mathrm{c} i}, $ | (3) |
| $ d_i=\frac{b}{2}-\left(180 \frac{E I L_i}{G J_{\mathrm{d}} R}+h_{\mathrm{d} i}\right) \geqslant h_{\mathrm{d} i}, $ | (4) |

|
| 图 2 三跨直线独柱墩梁桥修正倾覆轴示意图 Fig. 2 Schematic diagram of corrected overturning axis of three-span linear single-column pier girder bridge |
| |
式中,b为同一边墩处两边墩支座的间距;E为主梁弹性模量;I为截面惯性矩;G为主梁剪切模量;Jd为主梁转动惯量。
1.3 结果分析采用刚性倾覆轴法、折线倾覆轴法和修正倾覆轴法分别获得2座桥梁的抗倾覆效应和倾覆效应,取其比值得到抗倾覆稳定性系数,计算结果如表 1所示。
| 桥梁名称 | 计算方法 | 抗倾覆效应/(kN·m) | 倾覆效应/(kN·m) | 抗倾覆稳定性系数 |
| 广东省某桥 | 刚性倾覆轴法 | 9 215.36 | 5 821.45 | 1.58 |
| 折线倾覆轴法 | 5 923.49 | 8 319.51 | 0.71 | |
| 修正倾覆轴法 | 7 877.27 | 6 861.74 | 1.15 | |
| 江苏省某桥 | 刚性倾覆轴法 | 7 182.95 | 3 285.89 | 2.19 |
| 折线倾覆轴法 | 4 038.12 | 6 202.95 | 0.65 | |
| 修正倾覆轴法 | 5 163.21 | 5 027.47 | 1.03 |
桥梁在事故车辆荷载作用下发生倾覆时,达到抗倾覆承载能力极限状态,此时倾覆效应略大于抗倾覆效应,因此,桥梁将要发生倾覆破坏时临界状态下的抗倾覆稳定性系数(以下简称临界值)为1,以此为基础分析不同计算方法得到的抗倾覆稳定性系数的准确性。
由表 1可知:(1)刚性倾覆轴法对2座事故桥梁计算出的抗倾覆稳定性系数均较高,其计算结果与临界值偏差为58%~119%,高估了桥梁的抗倾覆承载能力,因此其结果偏不安全。(2)折线倾覆轴法基于小变形假定,忽视了在倾覆过程中自重对抗倾覆贡献逐渐增大的情况,导致计算结果与临界值偏差为-35%~-29%,从而低估了桥梁的抗倾覆能力。(3)修正倾覆轴法充分考虑了主梁在倾覆过程中的真实受力状况,且通过支座尺寸效应对倾覆轴线进行修正,以考虑桥梁自重产生的抗倾覆效应逐渐增大这一因素,其计算结果与临界值偏差为-12%~-5%,与实际情况较为符合,因此,修正倾覆轴法可较为准确地判断独柱墩梁桥的抗倾覆承载能力。
2 实测车流统计及随机车流模拟为得到更符合实际的车流数据,基于广东省某大桥动态称重(Weigh-in-Motion,WIM)系统进行实测车流数据采集,通过概率统计分析得到不同车辆参数的概率分布特征,建立随机车流模型。
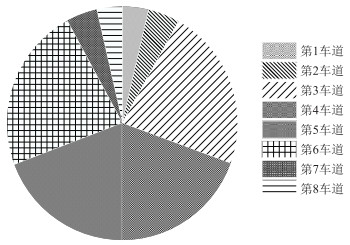
2.1 汽车荷载统计对广东省某大桥2022年11月份30 d的车流数据进行统计调查,共计调查车辆总数为1 276 959辆,日均车流量为42 565辆。该大桥双向共8条车道,第1车道至第4车道为桥梁的上行方向,第5车道至第8车道为下行方向。各车道车流量在车流总量中的占比如图 3所示。由图可知,上行方向的4个车道中第3车道和第4车道的车流量较大,占比分别为44.9%和38.8%;第1车道和第2车道的车流量较小,占比分别为7.4%和8.9%;下行方向的4个车道中第5车道和第6车道的车流量较大,占比分别为38.4%和45.7%;第7车道和第8车道的车流量较小,占比分别为8.7%和7.2%。
|
| 图 3 广东省某大桥各车道车流量占比(单位:%) Fig. 3 Proportion of traffic flow on each lane of certain bridge in Guangdong (unit: %) |
| |
2.1.1 车型分类
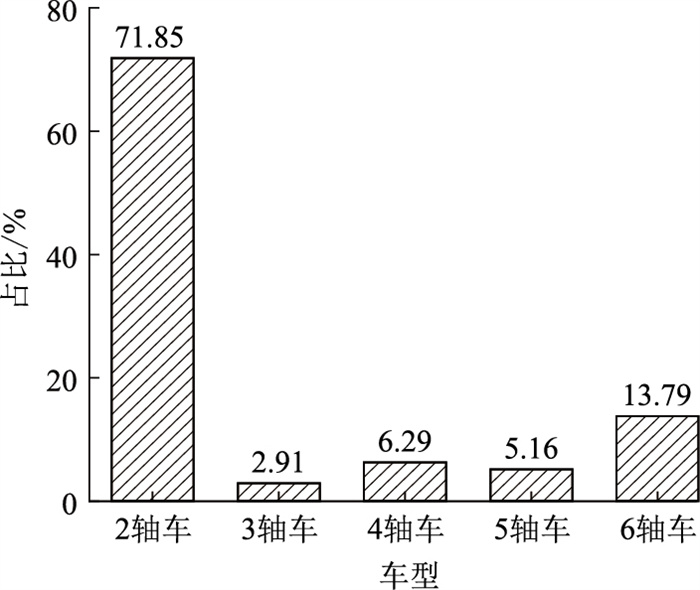
根据WIM系统实测车流数据,本研究将所有车辆分为5种代表车型:2轴车、3轴车、4轴车、5轴车和6轴车。统计得到各车型在车流量中的占比如图 4所示。由图可知,2轴车和6轴车的车辆数占比最大,分别为71.85%和13.79%,3轴车的车辆数占比最小,为2.91%。
|
| 图 4 广东省某大桥各车型车辆数占比 Fig. 4 Proportion of vehicle numbers of each model for certain bridge in Guangdong |
| |
车辆在不同车道行驶时产生的倾覆效应差别很大,而不同车型在各车道的数量占比有所差异,因此为准确分析桥梁的倾覆效应,需对各车道上不同车型的数量占比进行统计分析,结果如2所示。由表可知,第1车道和第8车道的6轴车占比最大,第2,3,6,7车道上2轴车占比较大,第4车道和第5车道上2轴车占比均超过99%,这说明重载车辆集中行驶于慢车道,快车道上行驶车辆大多数为2轴车。
| 车型 | 2轴车 | 3轴车 | 4轴车 | 5轴车 | 6轴车 |
| 第1车道 | 32.6 | 6.4 | 9.5 | 8.6 | 42.9 |
| 第2车道 | 66.4 | 5.1 | 7.4 | 4.9 | 16.2 |
| 第3车道 | 91.5 | 3.2 | 2.8 | 1.6 | 0.9 |
| 第4车道 | 99.0 | 0.4 | 0.1 | 0.3 | 0.2 |
| 第5车道 | 99.2 | 0.3 | 0.2 | 0.1 | 0.2 |
| 第6车道 | 96.7 | 1.4 | 0.8 | 0.6 | 0.5 |
| 第7车道 | 71.5 | 4.3 | 6.2 | 5.9 | 12.1 |
| 第8车道 | 24.3 | 7.8 | 12.9 | 15.2 | 39.8 |
2.1.2 车辆轴距和轴重
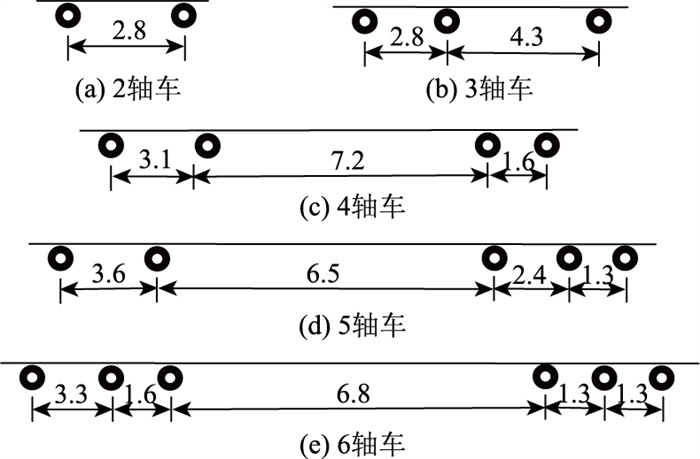
在模拟随机车流时,需根据不同车型模拟其轴距和对应轴重,因此有必要根据实测车流数据对不同车型的轴距和轴重进行统计分析。各车型轴距和轴重均值分别如图 5和表 3所示。
|
| 图 5 各车型轴距均值(单位:m) Fig. 5 Average wheelbase for each model (unit: m) |
| |
| 车型 | 1轴 | 2轴 | 3轴 | 4轴 | 5轴 | 6轴 | |
| 2轴车 | 轴重均值/kg | 1 561 | 229 3 | — | — | — | — |
| 比例/% | 40.5 | 59.5 | — | — | — | — | |
| 3轴车 | 轴重均值/kg | 3 715 | 3 598 | 6 910 | — | — | — |
| 比例/% | 26.1 | 25.3 | 48.6 | — | — | — | |
| 4轴车 | 轴重均值/kg | 5 538 | 6 712 | 6 956 | 7 014 | — | — |
| 比例/% | 21.1 | 25.6 | 26.5 | 26.8 | — | — | |
| 5轴车 | 轴重均值/kg | 6 819 | 9 353 | 6 697 | 6 145 | 6 346 | — |
| 比例/% | 19.3 | 26.4 | 18.9 | 17.4 | 17.9 | — | |
| 6轴车 | 轴重均值/kg | 7 566 | 8 610 | 8 923 | 9 340 | 9 184 | 9 256 |
| 比例/% | 14.3 | 16.3 | 16.9 | 17.7 | 17.4 | 17.5 |
2.1.3 车辆总重
采用高斯混合模型拟合不同车型的车重分布得到其概率统计参数,并对拟合结果进行K-S检验。高斯混合模型可以表示为:
| $ P\left\{w \mid\left(a_i, \mu_i, \sigma_i^2\right)\right\}=\sum\limits_{i=1}^m a_i \cdot g\left(w \mid \mu_i, \sigma_i^2\right), $ | (5) |
式中,w为车重;ai为第i个高斯混合模型子分布的权重,应满足
对该桥实测的不同车型车重数据进行拟合,结果如图 6所示。由图可知,高斯混合模型对各车型车辆总重的拟合结果较为准确。2轴车的车重较小,主要分布在1~5 t范围内;3轴车和4轴车的车重主要分布在10~50 t范围内;5轴车和6轴车车重主要分布在10~60 t和20~90 t范围内。各车型车重的高斯混合模型分布形式均为三参数高斯混合分布其参数如表 4所示。

|
| 图 6 各车型车辆总重概率密度 Fig. 6 Probability density of gross vehicle weight for each model |
| |
| 车型 | 分布参数 | ||
| 2轴车 | a1=0.908 | μ1=2.325 | σ1=0.512 |
| a2=0.050 | μ2=4.174 | σ2=0.511 | |
| a3=0.042 | μ3=7.956 | σ3=0.648 | |
| 3轴车 | a1=0.162 | μ1=37.846 | σ1=6.465 |
| a2=0.268 | μ2=58.153 | σ2=8.389 | |
| a3=0.570 | μ3=74.942 | σ3=2.197 | |
| 4轴车 | a1=0.162 | μ1=37.846 | σ1=6.465 |
| a2=0.268 | μ2=58.153 | σ2=8.389 | |
| a3=0.570 | μ3=74.942 | σ3=2.197 | |
| 5轴车 | a1=0.269 | μ1=19.785 | σ1=5.465 |
| a2=0.457 | μ2=41.319 | σ2=6.389 | |
| a3=0.274 | μ3=54.622 | σ3=3.197 | |
| 6轴车 | a1=0.570 | μ1=37.846 | σ1=6.465 |
| a2=0.068 | μ2=58.153 | σ2=8.389 | |
| a3=0.362 | μ3=74.942 | σ3=3.197 | |
2.1.4 车辆间距
WIM系统无法直接测得各车辆之间的车间距,因此需根据实测车速计算得到。
| $ S_i=V_i \times\left(T_{i+1}-T_i\right), $ | (6) |
式中,Si为第i辆车通过时的速度;Ti为第i辆车通过时的时刻;Ti+1为第i+1辆车通过时的时刻。
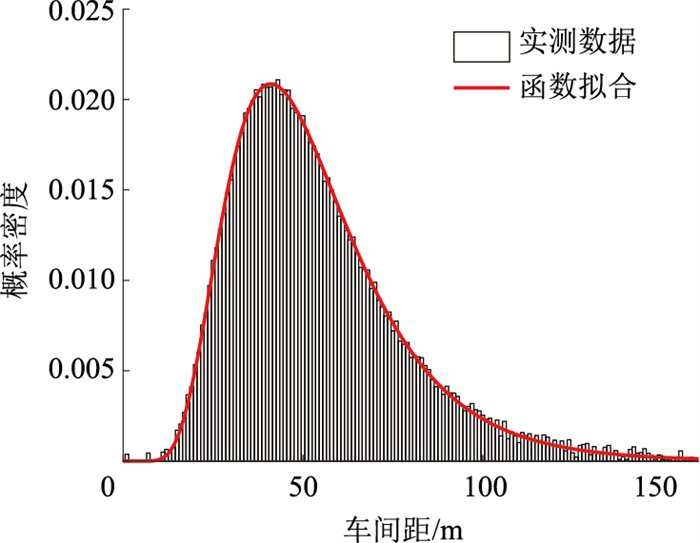
对式(6)得到的车间距拟合,并进行K-S检验,得到其服从对数正态分布,均值和方差分别为3.895和0.426。实测车间距大部分集中在20~120 m,其概率密度峰值约为40 m,如图 7所示。
|
| 图 7 车间距概率密度 Fig. 7 Probability density of vehicle spacing |
| |
2.2 随机车流模拟
基于各车辆参数的统计特性,首先确定使独柱墩桥梁产生最不利倾覆效应的车流工况,随后采用蒙特卡洛法生成随机车流模型。
2.2.1 随机车流下最不利倾覆效应工况分析独柱墩梁桥的桥宽基本介于8~10 m之间,车道布置为双车道。根据2.1.1节中各车道的车型占比发现,绝大多数重载车辆行驶于横桥向最外侧的慢车道,即第1车道和第8车道,其中第1车道的重载车辆数最多,而重载车辆偏载行驶会使独柱墩梁桥产生最不利的倾覆效应,因此模拟随机车流时选用第1车道的各车型数量占比模拟生成随机车流。
2.2.2 随机车流模拟流程及结果独柱墩梁桥的倾覆效应受多个车辆参数的影响。根据各车型占比、轴重、轴距、车辆总重及车辆间距的统计分析结果,采用蒙特卡洛法模拟随机车流。具体分为2个步骤。
步骤1:构造概率统计模型,尽可能准确地描述各随机参数的不确定性。
步骤2:从已知的概率分布抽样产生随机变量。采用舍选法对各车辆参数随机变量进行抽样,对于有限区间[a, b]上的随机变量X,其概率密度函数为fX(x),且fX(x)的上确界为
根据上述步骤,采用Matlab编制随机车流模拟程序,模拟得到365 d的车流量的随机车流,各车型车辆数如表 5所示。
| 车型 | 数量/辆 | 占比/% |
| 2轴车 | 5 064 809 | 32.6 |
| 3轴车 | 994 318 | 6.4 |
| 4轴车 | 1 475 941 | 9.5 |
| 5轴车 | 1 336 115 | 8.6 |
| 6轴车 | 6 665 042 | 42.9 |
| 总计 | 15 536 225 | 100.0 |
3 倾覆效应概率统计分析
超载车辆偏载行驶与规范产生的桥梁倾覆效应并不相同,采用其作为抗倾覆验算荷载无法保证桥梁抗倾覆的安全性。因此,基于第2节的实测车流数据,结合修正倾覆轴法和影响线加载法计算桥梁的倾覆效应并对其进行概率统计分析。
选取单跨跨径分别为20,30,40 m,跨数分别为3,4,5的独柱墩梁桥进行研究。曲率半径取200 m和∞这2种情况,分别代表曲线独柱墩梁桥和直线独柱墩梁桥。采用ANSYS19.2建立各独柱墩梁桥有限元模型,将单位集中力按横向最不利偏载位置加载于桥梁,并根据各桥梁修正倾覆轴的位置得到单位集中力加载于桥梁上各纵向位置(按0.1 m间距)时的倾覆效应,将其连线得到倾覆效应的影响线,以此为基础计算公路-Ⅰ级车道荷载和随机车流荷载下独柱墩梁桥的倾覆效应,并将其比值,即倾覆效应比(随机车流荷载作用产生的倾覆效应与规范车道荷载作用产生的倾覆效应之比)作为统计分析对象,研究规范车道荷载和随机车流荷载下倾覆效应的差异。
3.1 规范车道荷载倾覆效应基于修正倾覆轴法和影响线加载法,计算得到现行规范中公路Ⅰ级车道荷载下不同桥型独柱墩梁桥的倾覆效应,如表 6所示。由表可见,曲线独柱墩梁桥和直线独柱墩梁桥在公路Ⅰ级车道荷载下的倾覆效应变化规律相似;随着跨数和跨径的增加,倾覆效应逐渐增大。
| 桥梁类型 | 曲率半径/m | 集中荷载/kN | 均布荷载/(kN·m-1) | 倾覆效应/(kN·m) |
| 3×20 m | 200 | 300 | 10.5 | 1 007.8 |
| ∞ | 300 | 10.5 | 991.6 | |
| 3×30 m | 200 | 320 | 10.5 | 1 192.8 |
| ∞ | 320 | 10.5 | 1 175.4 | |
| 3×40 m | 200 | 340 | 10.5 | 1 452.3 |
| ∞ | 340 | 10.5 | 1 469.2 | |
| 4×20 m | 200 | 300 | 10.5 | 1 132.4 |
| ∞ | 300 | 10.5 | 1 147.5 | |
| 4×30 m | 200 | 320 | 10.5 | 1 354.1 |
| ∞ | 320 | 10.5 | 1 369.3 | |
| 4×40 m | 200 | 340 | 10.5 | 1 590.6 |
| ∞ | 340 | 10.5 | 1 606.2 | |
| 5×20 m | 200 | 300 | 10.5 | 1 283.2 |
| ∞ | 320 | 10.5 | 1 391.5 | |
| 5×30 m | 200 | 320 | 10.5 | 1 377.3 |
| ∞ | 300 | 10.5 | 1 297.1 | |
| 5×40 m | 200 | 340 | 10.5 | 1 589.1 |
| ∞ | 340 | 10.5 | 1 609.6 |
3.2 随机车流荷载倾覆效应
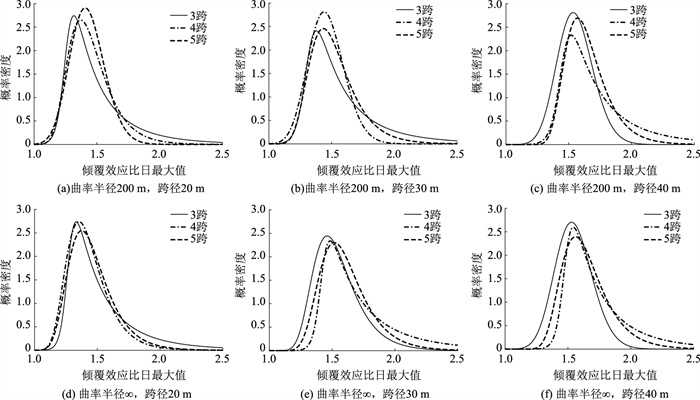
《公路工程结构可靠性设计统一标准》 (JTG 2120—2020)规定取设计基准期内荷载效应的年最大值分布确定其标准值,本研究将模拟的365 d的车流量均分为365份,计算每份产生的倾覆效应并提取其最大值,作为倾覆效应比的日最大值,以代替倾覆效应比的年最大值。倾覆效应比的日最大值概率密度如图 8所示,分布形式及误差如表 7所示。
|
| 图 8 倾覆效应比日最大值概率密度 Fig. 8 Daily maximum probability density of overturning effect ratio |
| |
| 桥梁类型 | 曲率半径/m | 分布形式 | 方差(误差) |
| 3×20 m | 200 | Burr分布 | 0.163 |
| 4×20 m | 200 | 极值分布 | 1.371 |
| 5×20 m | 200 | 对数正态分布 | 0.097 |
| 3×30 m | 200 | Burr分布 | 0.172 |
| 4×30 m | 200 | 对数正态分布 | 0.098 |
| 5×30 m | 200 | 极值分布 | 1.434 |
| 3×40 m | 200 | 对数正态分布 | 0.092 |
| 4×40 m | 200 | Burr分布 | 0.171 |
| 5×40 m | 200 | 极值分布 | 1.570 |
| 3×20 m | ∞ | Burr分布 | 0.135 |
| 4×20 m | ∞ | 极值分布 | 1.354 |
| 5×20 m | ∞ | 极值分布 | 1.376 |
| 3×30 m | ∞ | 极值分布 | 1.460 |
| 4×30 m | ∞ | Burr分布 | 0.116 |
| 5×30 m | ∞ | 极值分布 | 1.517 |
| 3×40 m | ∞ | 对数正态分布 | 0.096 |
| 4×40 m | ∞ | Burr分布 | 0.146 |
| 5×40 m | ∞ | 极值分布 | 1.560 |
由图 8可知,倾覆效应比的日最大值均大于1,即规范车道荷载作用产生的倾覆效应小于随机车流荷载作用产生的倾覆效应;当跨径相同时,随着跨数的增加,倾覆效应比的日最大值逐渐增大;当跨数相同时,随着跨径的增加,倾覆效应比日最大值亦逐渐增大;倾覆效应比的日最大值介于1.0~2.5之间,其峰值约为1.5,且随跨径和跨数的增加逐渐增大。随机车流荷载下独柱墩梁桥的倾覆效应明显大于规范车道荷载下的倾覆效应,这表明采用规范车道荷载进行抗倾覆稳定性分析偏不安全。因此,该大桥所处区域在后续独柱墩梁桥的抗倾覆设计及分析中应适当提高汽车荷载的取值标准。
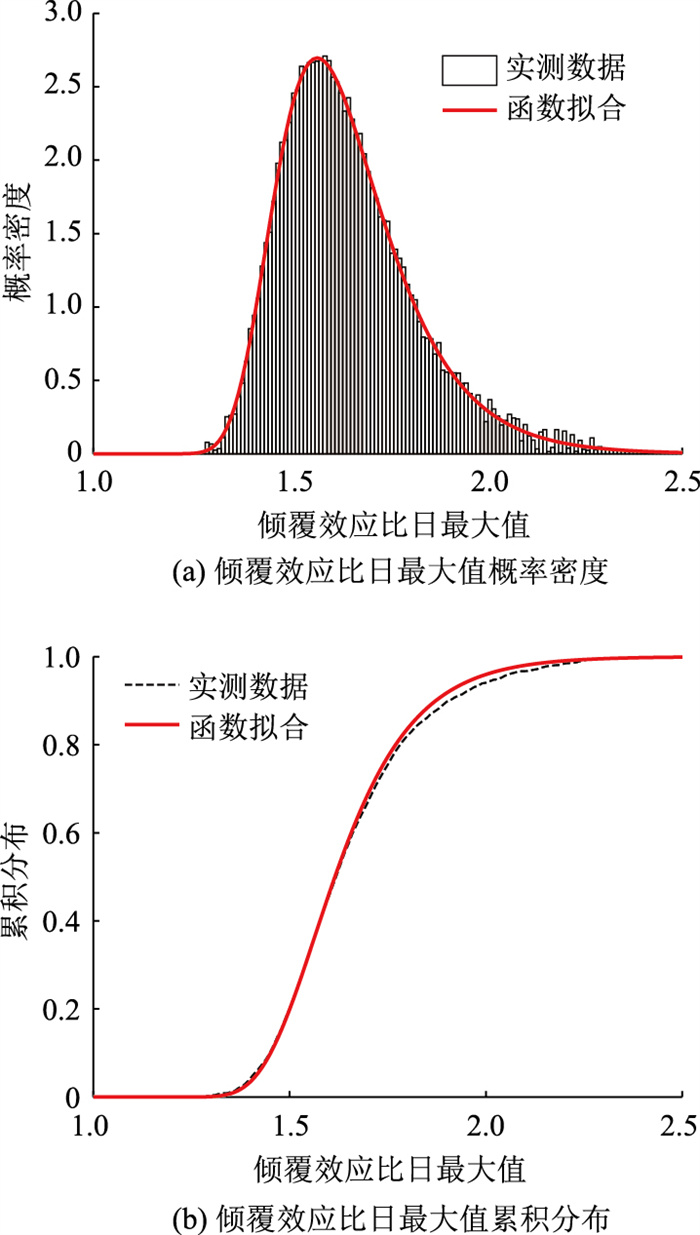
为得到更具代表性的倾覆效应比日最大值概率统计模型,将不同桥型的倾覆效应比进行归并,结果如图 9所示。使用最优函数拟合归并结果并进行K-S检验,确定倾覆效应比日最大值的概率分布为极值分布,其概率密度函数为:
| $ h(x)=7.3289 \mathrm{e}^{-7.3289(x-1.5702)-\mathrm{e}^{-7.3289(x-1.5702)}}, $ | (7) |
|
| 图 9 所有桥型倾覆效应比日最大值概率密度及累积分布 Fig. 9 Daily maximum probability density and cumulative distribution of all bridge overturning effect ratio |
| |
式中x为倾覆效应比。
采用与JTG 2120—2020一致的方法,取倾覆效应比日最大值概率密度函数的0.95分位值,得到根据实测车流数据计算出的倾覆效应标准值。根据式(7)得到倾覆效应比日最大值概率密度函数的0.95分位值为1.98,即大桥所处区域实测汽车荷载产生的倾覆效应为现行规范中公路Ⅰ级车道荷载的1.98倍。
4 基于目标可靠指标的桥梁抗倾覆稳定性分析方法当前研究多采用确定性分析模型计算桥梁的抗倾覆稳定性系数,以评估独柱墩梁桥的抗倾覆稳定性是否满足要求。该方法虽计算过程简便,却忽略了抗倾覆效应和倾覆效应均是随机变量的特性,导致其计算得到的抗倾覆稳定性系数并不能准确地评估独柱墩梁桥的抗倾覆安全储备。因此,本研究在不考虑墩柱强度破坏,界面滑移破坏的假设前提下,基于可靠度理论,根据上述倾覆效应研究,建立目标可靠指标与抗倾覆稳定性系数的联系,提出随机性分析模型并得到基于目标可靠指标的抗倾覆稳定性分析方法,以评估独柱墩梁桥的抗倾覆稳定性。
4.1 桥梁荷载效应随机变量结构的功能函数由结构抗力随机变量和荷载效应随机变量决定。对于桥梁抗倾覆分析,这两者分别为桥梁自重作用产生的抗倾覆效应随机变量和汽车荷载作用产生的倾覆效应随机变量。
4.1.1 抗倾覆效应随机变量桥梁自重因受材料性能和几何参数等不确定因素的影响而并非定值,对其进行统计分析极为困难。因此,采用规范中的桥梁自重概率统计模型,即:
| $ F_{\mathrm{G}}(x)=\frac{1}{\sqrt{2 \pi} \sigma_{\mathrm{G}}} \int_{-\infty}^x \mathrm{e}^{-\frac{\left(x-\mu_{\mathrm{G}}\right)^2}{2 \sigma_{\mathrm{G}}^2}} \mathrm{~d} x, $ | (8) |
| $ \mu_{\mathrm{G}}=K_{\mathrm{G}} G_{\mathrm{K}}, $ | (9) |
| $ \sigma_{\mathrm{G}}=\mu_{\mathrm{G}} \delta_{\mathrm{K}}, $ | (10) |
式中,μG为自重平均值;KG为自重均值系数;GK为自重标准值;σG为自重标准差;δK为自重变异系数。桥梁自重服从正态分布,而桥梁自重由桥面和构件组成,因此规范分别给出了二者的统计参数,如表 8所示。
| 位置 | 均值系数 | 变异系数 |
| 水泥混凝土桥面 | 0.986 5 | 0.098 0 |
| 沥青混凝土桥面 | 0.989 1 | 0.111 4 |
| 构件 | 1.021 2 | 0.046 2 |
JTG 2120—2020将桥梁自重不同组成部分的均值系数和变异系数进行组合,得到桥梁自重的统计参数KG=1.014 8,δK=0.043 1。考虑到桥梁抗倾覆效应由桥梁自重作用产生,因此可近似地将桥梁自重概率统计模型视为抗倾覆效应随机变量的概率统计模型,得到其概率分布函数。
| $ S_{\mathrm{bk}}(x)=\frac{1}{\sqrt{2 \pi} \sigma_{\mathrm{bk}}} \int_{-\infty}^x \mathrm{e}^{-\frac{\left(x-\mu_{\mathrm{bk}}\right)^2}{2 \sigma_{\mathrm{bk}}^2}} \mathrm{~d} x, $ | (11) |
| $ \mu_{\mathrm{bk}}=K_{\mathrm{bk}} S_{\mathrm{bk}}, $ | (12) |
| $ \sigma_{\mathrm{bk}}=\mu_{\mathrm{bk}} \delta_{\mathrm{bk}}, $ | (13) |
式中,μbk为抗倾覆效应平均值;Kbk为抗倾覆效应均值系数;Sbk为抗倾覆效应标准值;σbk为抗倾覆效应标准差;δbk为抗倾覆效应变异系数。由此可得结构抗倾覆效应的均值系数Kbk=KG=1.014 8,变异系数δbk=δK=0.043 1。
4.1.2 倾覆效应随机变量根据倾覆效应日最大值的统计分析结果可知,抗倾覆分析汽车荷载模型作用下的桥梁倾覆效应随机变量的概率分布函数为:
| $ S_{\mathrm{sk}}(x)=\int_{-\infty}^x S_{\mathrm{sk}} \cdot h(x) \mathrm{d} x, $ | (14) |
式中,Ssk为倾覆效应标准值,即公路Ⅰ级车道荷载作用下的倾覆效应;h(x)为倾覆效应比日最大值的概率密度函数。
4.2 桥梁抗倾覆稳定性分析模型 4.2.1 确定性分析模型在确定性分析模型中,采用自重作用产生的抗倾覆效应标准值与汽车荷载产生的倾覆效应标准值进行独柱墩梁桥的抗倾覆稳定性分析。本研究选取桥跨布置均为3×25 m,曲率半径分别为200 m和∞的独柱墩桥梁进行抗倾覆计算分析,结构形式如图 10所示。

|
| 图 10 桥梁结构示意图(单位:cm) Fig. 10 Schematic diagrams of bridge structure (unit: cm) |
| |
根据修正倾覆轴法计算得到2座桥梁的抗倾覆效应标准值、倾覆效应标准值和抗倾覆稳定性系数,计算结果如表 9所示。
| 曲率半径/m | 抗倾覆效应标准值/(kN·m) | 倾覆效应标准值/(kN·m) | 抗倾覆稳定性系数 |
| 200 | 7 877.27 | 2 351.87 | 3.35 |
| ∞ | 4 349.05 | 2 294.21 | 1.89 |
4.2.2 随机性分析模型
确定性分析模型仅取抗倾覆效应标准值和倾覆效应标准值之比作为独柱墩梁桥的抗倾覆稳定性系数,无法考虑各种随机因素对抗倾覆稳定性的影响。因此,根据可靠度理论,将抗倾覆效应当做随机变量,根据独柱墩梁桥倾覆极限状态的功能函数计算特定目标可靠指标β下的抗倾覆稳定性系数,建立抗倾覆稳定性分析的随机性模型。独柱墩梁桥倾覆极限状态的功能函数为:
| $ Z=g\left[S_{\mathrm{bk}}(x), S_{\mathrm{sk}}(x)\right]=S_{\mathrm{bk}}(x)-k_{\mathrm{qf}}^\beta S_{\mathrm{sk}}(x), $ | (15) |
式中,Sbk(x)为抗倾覆效应随机变量;Ssk(x)为倾覆效应随机变量。
式(14)中抗倾覆稳定性系数为待求解参数。基于随机性分析模型中目标可靠指标确定独柱墩梁桥抗倾覆稳定性系数的迭代计算步骤如下:
(1) 给定抗倾覆稳定性系数的初值(本研究取0)和目标可靠指标β,本研究取β=5.2,即对应一级安全等级脆性破坏的目标可靠指标。
(2) 由表 9得到独柱墩梁桥的抗倾覆效应标准值和倾覆效应标准值,利用JC法,结合式(11)~(14),计算功能函数(15)的可靠度指标β(0)。
(3) 若
| 曲率半径/m | 目标可靠性指标 | 抗倾覆稳定性系数kqfβ |
| 200 | 5.2 | 2.29 |
| ∞ | 5.2 | 1.26 |
基于确定性分析模型计算得到的2座桥梁的抗倾覆稳定性系数分别为3.35和1.89。然而,在目标可靠指标为5.2的条件下,基于随机性分析模型计算得到的抗倾覆稳定系数分别为2.29和1.26,相对于确定性分析模型,降幅分别为31.6%和33.3%。由此可见,与确定性分析模型相比,随机性分析模型得到的抗倾覆稳定系数明显较小。这一差异表明,确定性分析模型在计算过程中将倾覆效应和抗倾覆效应当作定值的做法未能充分考虑桥梁在实际运营过程中荷载效应的随机性,计算所得的抗倾覆稳定性系数偏大,从而高估了独柱墩梁桥的抗倾覆稳定性;而随机性分析模型将荷载效应当作随机变量处理,能够较为准确地判断独柱墩梁桥抗倾覆稳定性,其计算得到的抗倾覆稳定性系数可用作评价独柱墩梁桥抗倾覆稳定性的量化指标。因此,应采用随机性分析模型,通过基于目标可靠指标的抗倾覆分析方法评价独柱墩梁桥的抗倾覆稳定性。
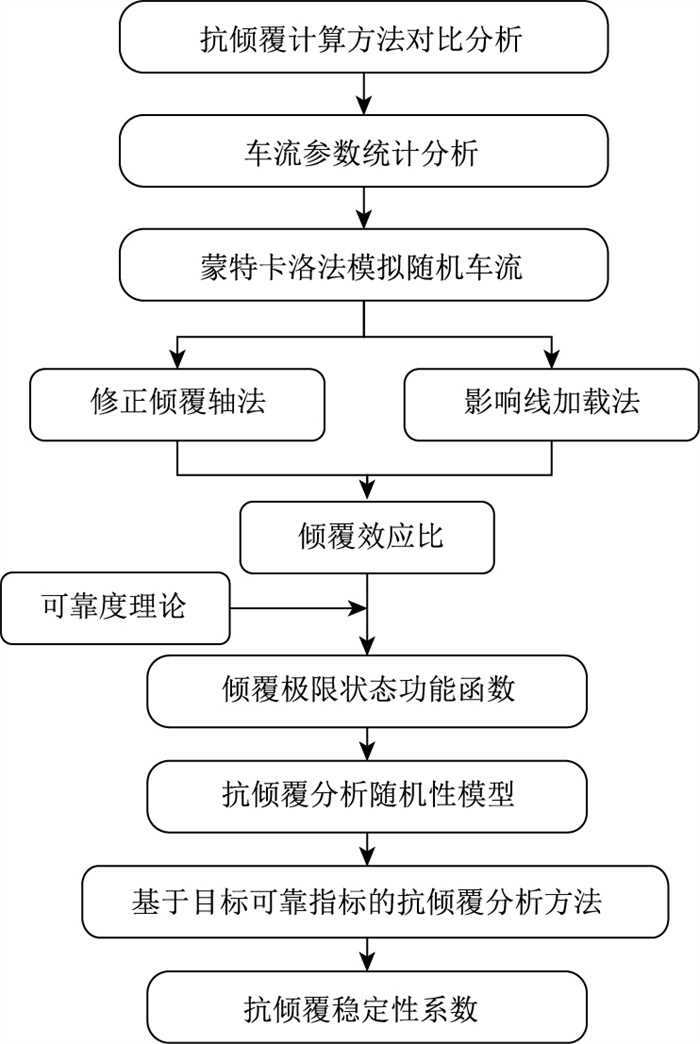
4.3 目标可靠指标下的抗倾覆稳定性分析方法基本框架及研究局限性目标可靠指标下的抗倾覆稳定性分析方法基本框架如图 11所示。本研究对目标可靠指标下的独柱墩梁桥抗倾覆稳定性进行了研究,具有一定的参考价值,但也存在局限性。随机车流受区域经济发展水平等因素影响较大。本研究仅根据广东省某大桥实测车流数据统计了各汽车荷载参数的概率统计分布模型,所建立的随机车流模型也仅能适用于该地区的独柱墩梁桥抗倾覆稳定性分析。其次,独柱墩梁桥的抗倾覆稳定性受桥梁结构和荷载作用2方面的影响,本研究仅针对随机车流荷载对独柱墩梁桥抗倾覆稳定性的影响规律,未来研究可从结构参数入手,进一步探讨其对独柱墩梁桥抗倾覆稳定性的影响规律。
|
| 图 11 目标可靠指标下的抗倾覆稳定性分析方法基本框架 Fig. 11 Basic framework of anti-overturning stability analysis method with target reliable indicators |
| |
5 结论
本研究结合实测随机车流荷载效应,基于目标可靠指标研究了独柱墩梁桥的抗倾覆稳定性,得出如下结论。
(1) 刚性倾覆轴法过高地估算了桥梁的抗倾覆能力,与实际倾覆破坏情况相比,其计算得到的抗倾覆稳定性系数的偏差为58%~119%,而折线倾覆轴法低估了桥梁的抗倾覆承载能力,其偏差为-35%~-29%,基于修正倾覆轴法计算得到的桥梁抗倾覆稳定性系数误差为-12%~-5%,相对较小,因此该方法可较为准确地评估独柱墩梁桥的抗倾覆承载能力。
(2) 独柱墩梁桥的倾覆效应比日最大值具有较大的波动性。针对本研究所研究的跨径及跨数,当独柱墩梁桥的跨径相同时,随着跨数的增加,倾覆效应比逐渐增大;当跨数相同时,随着跨径的增加,倾覆效应比亦逐渐增大。
(3) 不同桥型独柱墩梁桥倾覆效应比的日最大值分布概率统计模型有所差异,将不同桥型的倾覆效应比日最大值进行归并,确定倾覆效应比日最大值的概率分布为极值分布,其0.95分位值为1.98,即该大桥所处区域实测汽车荷载产生的倾覆效应为现行规范中公路Ⅰ级车道荷载的1.98倍。
(4) 在目标可靠指标为5.2的条件下,基于随机性分析模型计算得到的抗倾覆稳定系数分别为2.29和1.26,相对于确定性分析模型,分别减少了1.06和0.63,降幅分别为31.6%和33.3%。
| [1] |
吉伯海, 傅中秋. 近年国内桥梁倒塌事故原因分析[J]. 土木工程学报, 2010, 43(增1): 495-498. JI Bohai, FU Zhongqiu. Analysis of Chinese bridge collapse accident causes in recent years[J]. China Civil Engineering Journal, 2010, 43(S1): 495-498. |
| [2] |
DENG L, WANG W, YU Y. State-of-the-art review on the causes and mechanisms of bridge collapse[J/OL]. Journal of Performance of Constructed Facilities, 2015, 30(2). (2015-01-09)[2025-02-01]. https://doi.org/10.1061/(ASCE)CF.1943-5509.0000731.
|
| [3] |
彭卫兵, 沈佳栋, 唐翔, 等. 近期典型桥梁事故回顾、分析与启示[J]. 中国公路学报, 2019, 32(12): 132-144. PENG Weibing, SHEN Jiadong, TANG Xiang, et al. Review, analysis, and insights on recent typical bridge accidents[J]. China Journal of Highway and Transport, 2019, 32(12): 132-144. |
| [4] |
李会驰, 刘晓娣, 冯苠. 箱梁匝道桥运营期倾覆风险管理[J]. 公路, 2016, 61(7): 88-93. LI Huichi, LIU Xiaodi, FENG Min. Overturning risk management of box-girder ramp bridge in operation period[J]. Highway, 2016, 61(7): 88-93. |
| [5] |
姜爱国, 杨志. 独柱墩曲线梁桥倾覆轴线研究[J]. 世界桥梁, 2013, 41(4): 58-61. JIANG Aiguo, YANG Zhi. Study of overturning axis of curved beam bridge with single-column piers[J]. World Bridges, 2013, 41(4): 58-61. |
| [6] |
周勇军, 王业路, 赵煜, 等. 公路独柱墩桥梁抗倾覆研究综述[J]. 交通运输工程学报, 2022, 22(6): 46-66. ZHOU Yongjun, WANG Yelu, ZHAO Yu, et al. Review on research of anti-overturning of highway bridges with single-column piers[J]. Journal of Traffic and Transportation Engineering, 2022, 22(6): 46-66. |
| [7] |
陈宝春, 黄冀卓, 余印根. 桥梁抗倒塌能力鲁棒性设计研究[J]. 重庆交通大学学报(自然科学版), 2014, 33(1): 1-7. CHEN Baochun, HUANG Jizhuo, YU Ying'en. Robustness design of bridges collapse resistance[J]. Journal of Chongqing Jiaotong University (Natural Sciences), 2014, 33(1): 1-7. |
| [8] |
彭卫兵, 徐文涛, 陈光军, 等. 独柱墩梁桥抗倾覆承载力计算方法[J]. 中国公路学报, 2015, 28(3): 66-72. PENG Weibing, XU Wentao, CHEN Guangjun, et al. Calculation method for anti-overturning capacity of single column pier girder-bridge[J]. China Journal of Highway and Transport, 2015, 28(3): 66-72. |
| [9] |
彭卫兵, 潘若丹, 马俊, 等. 独柱墩梁桥倾覆破坏模式与计算方法研究[J]. 桥梁建设, 2016, 46(2): 25-30. PENG Weibing, PAN Ruodan, MA Jun, et al. Study of overturning failure modes and anti-overturning calculation methods for single-column pier beam bridges[J]. Bridge Construction, 2016, 46(2): 25-30. |
| [10] |
曹景, 刘志才, 冯希训. 箱形截面直线桥及曲线桥抗倾覆稳定性分析[J]. 桥梁建设, 2014, 44(3): 69-74. CAO Jing, LIU Zhicai, FENG Xixun. Analysis of overturning stability of straight and curved bridges with box sections[J]. Bridge Construction, 2014, 44(3): 69-74. |
| [11] |
WANG Y L, ZHOU Y J, XUE Y X, et al. Failure analysis for overall overturning of concrete single-column pier bridges induced by temperature and overloaded vehicles[J/OL]. Materials, 2024; 17(11): 2650. (2024-05-30)[2025-02-01]. https://doi.org/10.3390/ma17112650.
|
| [12] |
MICHALTSOS G T, RAFTOYIANNIS I G. A mathematical model for the rocking, overturning and shifting problems in bridges[J].
Engineering Structures, 2008, 30(12): 3587-3594.
|
| [13] |
庄冬利. 偏载作用下箱梁桥抗倾覆稳定问题的探讨[J]. 桥梁建设, 2014, 44(2): 27-31. ZHUANG Dongli. Study of overturning stability issues of box girder bridges under action of eccentric load[J]. Bridge Construction, 2014, 44(2): 27-31. |
| [14] |
徐亚峰, 付晓, 关波, 等. 基于多目标优化的独柱墩直线梁桥抗倾覆加固[J]. 公路交通科技, 2024, 41(6): 109-118. XU Yafeng, FU Xiao, GUAN Bo, et al. Anti-overturning reinforcement for single-column pier straight beam bridge based on multi-objective optimization[J]. Journal of Highway and Transportation Research and Development, 2024, 41(6): 109-118. DOI:10.3969/j.issn.1002-0268.2024.06.012 |
| [15] |
DENG T F, ZHANG J P, LI S, et al. Anti-overturning stability coefficient of curved girder bridges considering seismic action[J].
Journal of Vibroengineering, 2019, 21(3): 710-725.
|
| [16] |
ZHUANG D L, XIAO R C, JIA L J, et al. Failure analysis for overall stability against sliding and overturning of a girder bridge[J/OL]. Engineering Failure Analysis, 2020, 109: 104271. https://doi.org/10.1016/j.engfailanal.2019.104271.
|
| [17] |
PENG W B, ZHAO H, DAI F, et al. Analytical method for overturning limit analysis of single-column pier bridges[J/OL]. Journal of Performance of Constructed Facilities, 2017, 31(4). https://doi.org/10.1061/(ASCE)CF.1943-5509.0000999.
|
| [18] |
陈水生, 赵辉, 李锦华, 等. 实际车流荷载作用的混凝土梁桥可靠度评估[J]. 振动与冲击, 2022, 41(20): 158-167. CHEN Shuisheng, ZHAO Hui, LI Jinhua, et al. Reliability assessment of a concrete beam bridge under actual traffic load[J]. Journal of Vibration and Shock, 2022, 41(20): 158-167. |
| [19] |
刘健, 晏铖, 方其样, 等. 基于响应面法与JC法结合的大跨度桥梁可靠度分析[J]. 桥梁建设, 2022, 52(4): 32-38. LIU Jian, YAN Cheng, FANG Qiyang, et al. Reliability analysis of long-span bridges based on combination of response surface method and JC method[J]. Bridge Construction, 2022, 52(4): 32-38. |
| [20] |
周勇军, 孙婧, 梁玉照. 公路桥梁设计荷载基本组合的分项系数值及其效应对比[J]. 公路, 2012, 57(1): 103-107. ZHOU Yongjun, SUN Jing, LIANG Yuzhao. Comparison of partial coefficient values and their effects of basic load combinations for highway bridges[J]. Highway, 2012, 57(1): 103-107. |
| [21] |
吴腾, 葛耀君, 熊洁. 现行国内外公路桥梁汽车荷载及其响应的比较[J]. 结构工程师, 2008, 24(5): 130-136. WU Teng, GE Yaojun, XIONG Jie. Live load and its reponse of highway bridges based on international and domestic design codes[J]. Structural Engineers, 2008, 24(5): 130-136. |
| [22] |
杨晓艳, 贡金鑫, 冯云芬. 不同跨径桥梁车辆荷载分项系数及可靠度[J]. 中国公路学报, 2015, 28(6): 59-66. YANG Xiaoyan, GONG Jinxin, FENG Yunfen. Partial factors of vehicle loads and reliability analysis of bridges with different spans[J]. China Journal of Highway and Transport, 2015, 28(6): 59-66. |
| [23] |
王业路. 中墩点支撑公路连续梁桥整体倾覆演化模型及计算方法研究[D]. 西安: 长安大学, 2023. WANG Yelu. Research on the evolution model and calculation method of the overall overturning of the continuous beam bridge supported by the middle pier point[D]. Xi 'an: Chang 'an University, 2023. |
| [24] |
PENG W B, TANG Z W, WANG D Z, et al. A forensic investigation of the Xiaoshan ramp bridge collapse[J/OL]. Engineering Structures, 2020, 224: 111203. (2020-12-01)[2025-02-01]. https://doi.org/10.1016/j.engstruct.2020.111203.
|
| [25] |
彭卫兵, 朱志翔, 谭超, 等. 强倾弱弯梁桥设计准则研究[J]. 中国公路学报, 2021, 34(2): 155-161. PENG Weibing, ZHU Zhixiang, TAN Chao, et al. Strong overturning-weak bending design criterion for girder bridges[J]. China Journal of Highway and Transport, 2021, 34(2): 155-161. |
 2025, Vol. 42
2025, Vol. 42



 ,
,