0 引言

随着经济发展和城市化的需要，城市面积迅速扩大，城市居民和汽车保有量迅速增加。汽车数量激增导致城市产生交通拥堵等一系列问题。准确的交通流预测有助于交通智能诱导、实现道路规划方便智能出行。交通流数据作为复杂的时空数据对其进行准确的建模需要从时间与空间两个维度出发，并把握交通流数据的动态变化模式进行学习，从而实现对城市交通流的精准预测。

早期的交通流预测方法通常是基于统计学理论的方法，例如历史均值模型(Historical Average, HA)^[1]等。该类方法基于线性特征处理时间序列，处理复杂非线性的交通流数据能力有限。为捕获交通流数据中复杂的非线性关系一些机器学习模型^[2]被应用于交通流预测，例如支持向量回归(Support Vector Regression, SVR)^[3]等。

相比于上述传统方法，深度学习在自动捕获特征和学习数据内复杂关系方面具有优势。部分研究者使用循环神经网络的变体(Long Short-Term Memory，LSTM)^[4]和(Gate Recurrent Unit，GRU)^[5]来捕获交通数据中的时间相关性。但上述方法仅考虑交通数据在时间维度的相关性而忽视了交通路网的空间相关性，因此，会导致模型具有局限性。Yao^[6]将交通路网划分为网格，采用卷积神经网络(Convolution Neural Network, CNN)和LSTM捕获交通路网的空间相关性和时间相关性。然而CNN更适用于具有规则网格的欧几里得数据，建模不规则的交通路网不可避免地会丢失路网的拓扑信息。为解决这一问题，研究人员采用处理图数据的图神经网络(Graph Neural Network, GNN)^[7]挖掘复杂交通数据的空间相关性。例如Li^[8]在图数据中使用双向随机游走的扩散模型捕获交通路网的空间相关性。Yu^[9]采用切比雪夫网络泛化的时空图方法捕获交通数据的时空相关性，以低成本计算方式提高预测精度。交通路网图中节点之间的关系是随时间变化的动态体系，前述方法使用预定义的固定图结构捕获空间相关性，在针对长时间步的预测任务下模型性能会降低。为此，Wu^[10]提出的Graph WaveNet设计一种自适应邻接矩阵来捕获复杂动态空间相关性并结合时间卷积网络挖掘时间相关性从而提高模型预测精度。Bai^[11]构造一种结合自适应图结构的循环神经网络，能自适应地挖掘交通路网的时空特征。这些研究在获取交通流动态特征方面取得较好效果，但它们仅依赖于构建的自适应邻接矩阵而没考虑基于节点(传感器)间连接距离的邻接矩阵，即忽略了预定义的固定图结构。Guo^[12]指出相同路网节点的交通流在不同时间尺度下会呈现出高度相似性，利用时间和空间注意力机制对多时间尺度进行时空相关性建模解决交通流长时间步的预测问题。谷振宇^[13]和黄艳国^[14]也通过挖掘交通流序列中潜在的时空性和周期性构建交通流预测模型。交通流预测本质上还是时间序列预测，前述方法多使用循环神经网络(Recurrent Neural Network, RNN)和时间卷积网络(Temporal Convolutional Network, TCN)^[15]提取时间特征，这些方法在长时间步的预测问题上存在缺陷且计算量较大。部分研究方法^[16-17]提出同步捕获时空相关性的观点，表明独立的特征捕获模块无法挖掘交通数据的时间相关性与空间相关性之间存在的因果关系。

基于上述研究存在的问题与启发，本研究提出一种基于多尺度下采样卷积交互的动态图卷积网络(Multi-Scale Downsampling Convolutional Interaction Dynamic Graph Convolution Neural Network, MDDGCNN)来同步捕获时空特性。本研究的主要贡献如下:

(1) 基于交通流数据的周期性特征，以当前相邻时段、上一日同一时段和上一周同一时段作为输入数据表达多尺度下交通流数据的时间相似性，并通过注意力机制解决交通流数据的周期性扰动问题。

(2) 基于邻近节点间的相关性，融合预定义邻接矩阵与自适应邻接矩阵生成动态图结构捕获交通流数据动态变化的空间相关性。

(3) 采用交互式学习策略捕获交通流数据的时间相关性，并将捕获空间特征的动态图模块嵌入其中以同步捕获时空特征。这使每个模块都具有整个序列的局部和全局信息进而提取有用的时空特征。

1 问题定义

交通路网图由交通道路观测点（传感器或路段）所在位置构成，将其定义为图$G=(V, E, A)$。其中$V$为节点集，$V \in \mathbb{R}^N ; E$为边的集合，表示节点间的连通性；图$G$的邻接矩阵为$\boldsymbol{A} \in \mathbb{R}^{\mathrm{N} \times \mathrm{N}}$，其中N为自然数集。交通流预测任务利用历史交通流序列$\left(X_{(t-T+1) G}, X_{(t-T+2) G}, \cdots, X_{(t) G}\right)$，预测未来的交通流序列$\left(X_{(t+1) G}, X_{(t+2) G}, \cdots, X_{\left(t+T^v\right) G}\right)$。其中$X_{(t) G} \in$ $\mathbb{R}^{N \times C}$表示在时间步$t$处对图$G$的观察；$C$为特征通道数量；$T$为给定历史时间序列长度；$T^{\prime}$为待预测时间序列的长度；$f$为学习历史序列信息的函数。交通流预测任务定义如式(1)所示。

$ f:\left[X_G^{(t-T+1)}, \cdots, X_G^{(t)}\right] \rightarrow\left[X_G^{(t+1)}, \cdots, X_G^{\left(t+T^{\prime}\right)}\right]。$

(1)

2 MDDGCNN模型 2.1 总体框架

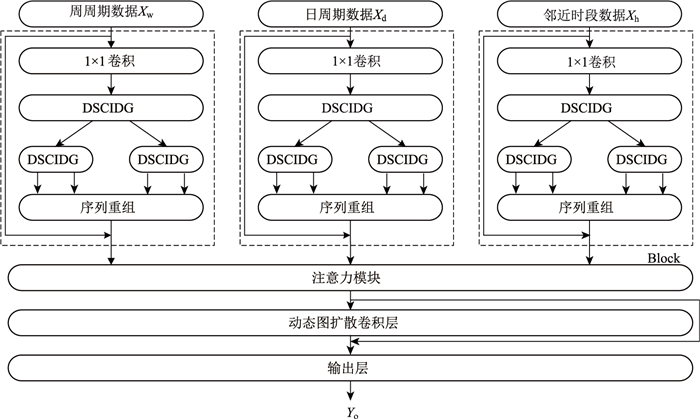
MDDGCNN模型的总体框架如图 1所示，通过树形结构的下采样卷积交互动态图模块(DSCIDG)同步捕获交通流数据在周、日和邻近时段这3个时间尺度下的时空相关性，并引入残差连接^[18]减少训练中的特征损失。

MDDGCNN具体工作流程如下：3个尺度下的原始输入数据($X_{\mathrm{w}} \in \mathbb{R}^{B x 1 \times N \times T}, \quad X_{\mathrm{d}} \in \mathbb{R}^{B x 1 \times N \times T}, \quad X_{\mathrm{h}} \in\mathbb{R}^{B x 1 \times N \times T} $) 都由3个相同的Block进行处理。首先，通过1×1卷积层将特征维数映射到高维空间以捕获更深层次的依赖关系。然后将高维特征数据输入至下采样卷积交互动态图模块(DSCIDG)，通过树形结构总共生成4个子序列(序列长度为T/4)。4个子序列按时间索引顺序进行重组得到新的序列(序列长度为T)。基于注意力机制解决周期性扰动问题以捕获稳定的时空相似性。最后，通过动态图卷积层把控全局时空特征，通过输出层得到预测值Y_o∈$\mathbb{R}^{B x 1 \times N \times T} $，其中B为批次大小；N为节点个数；T为序列长度。

2.2 时间相关性分析

交通流数据受人的出行因素影响表现出一定的相似规律性。通过Pearson相关系数(系数大于0.6为强相关，大于0.8为极强相关)对PeMS数据集中交通流量数据进行时间相关性分析。日周期时间相关性如图 2所示，以多个检测器为例，连续工作日之间交通流呈现高相关性，工作日与非工作日之间也呈现出较高相关性。周周期时间相关性如图 3所示，连续五周相关系数均大于0.8，表现高相关性。图 2与图 3中相关系数为每天同一时刻系数值求和后的平均值，表明交通流数据在时间上表现出较高相关性。

2.3 多尺度特征输入

基于交通流数据多时间尺度上呈现的高度相似性，本研究构建预测所需的相邻时段、上一日同一时段和上一周同一时段的3种时间尺度作为模型的输入数据以捕获路网节点间长短期的时间作用关系。

如图 4所示，设预测的时间序列长度为T_p，相邻时段时间序列长度、上一日同时段时间序列长度和上一周同时段时间序列长度分别为T_h，T_d和T_w，当前时刻为t₀，即用过去1 h(12个连续时间切片数据)的流量数据预测未来1 h流量数据(每5 min为一次数据信息，共12个值)。3个时间尺度的时间序列定义为X_h，X_d，X_w，如式(2)~(4)所示。

$ X_{\mathrm{h}}=\left(X_{t_0-T_{\mathrm{h}}+1}, X_{t_0-T_{\mathrm{h}}+2}, \cdots, X_{t_0}\right) \in \mathbb{R}^{C \times N \times T}, $

(2)

式中，X_h为与预测时段相邻的一段历史时间序列，对应区间为T_h；C为特征通道数量；N为节点数量；T为给定历史时间序列长度。

$ X_{\mathrm{d}}=\left(X_{t_0-q+1}, X_{t_0-q+2}, \cdots, X_{t_0-q+T_{\mathrm{p}}}\right) \in \mathbb{R}^{C \times N \times T}, $

(3)

式中，X_d为与预测时段相同的昨日历史时间序列，对应区间为T_d；q为传感器每天采样频率。

$ X_{\mathrm{w}}=\left(X_{t_0-7 \times q+1}, X_{t_0-7 \times q+2}, \cdots, X_{t_0-7 \times q+T_{\mathrm{p}}}\right) \in \mathbb{R}^{C \times N \times T}, $

(4)

式中，X_w为与预测时段相同的上周历史时间序列，对应区间为T_w。

2.4 下采样卷积交互

SCINet^[19]通过交互式学习策略和CNN处理具有复杂时间动态的时间序列。基于CNN的时间特征捕获方法也用于交通数据，如Graph WaveNet^[10]。经典的时间特征挖掘模型主要为RNN(包含LSTM和GRU)、Transformer和TCN。相比于RNN和Transformer，CNN局部特征提取能力强，且可以并行处理数据降低计算量；相比于TCN，交互式学习结构能捕捉长期依赖关系，且能在不同时间尺度上进行建模。

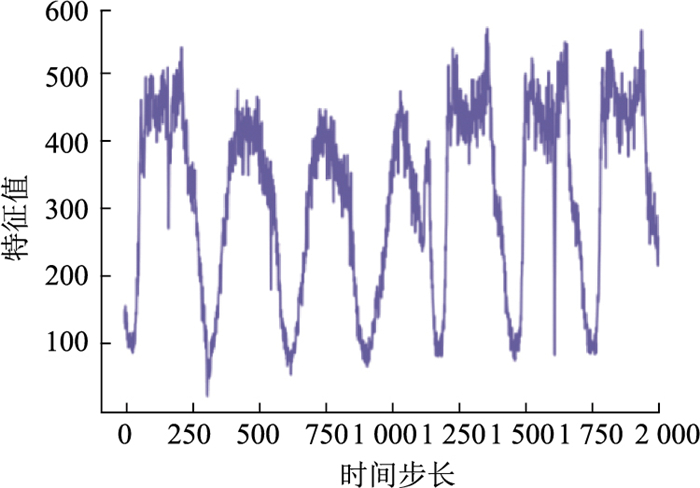
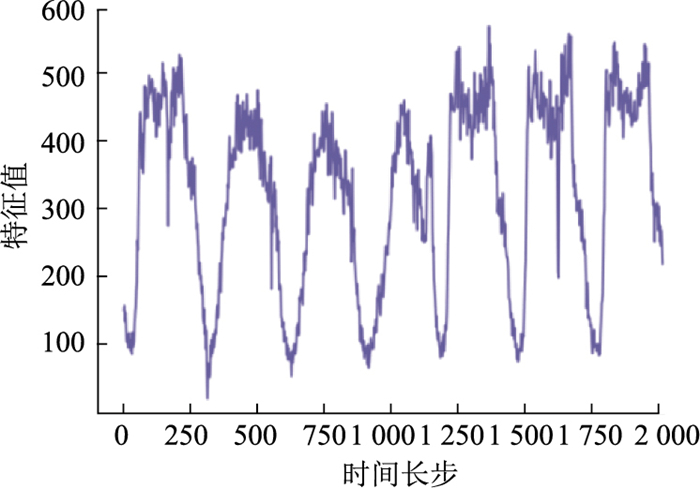
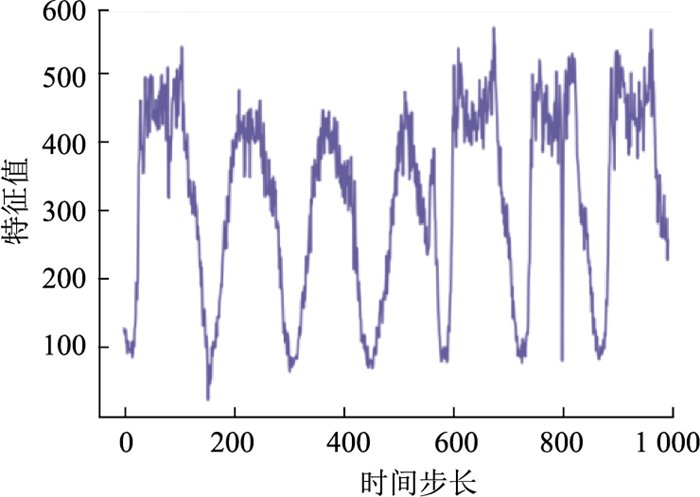
由于时间序列的临近性和特殊性，分割的子序列仍保留原始序列大部分特征趋势，如图 5~7所示。基于该特性，采用下采样卷积交互结构同步捕获时空特征。

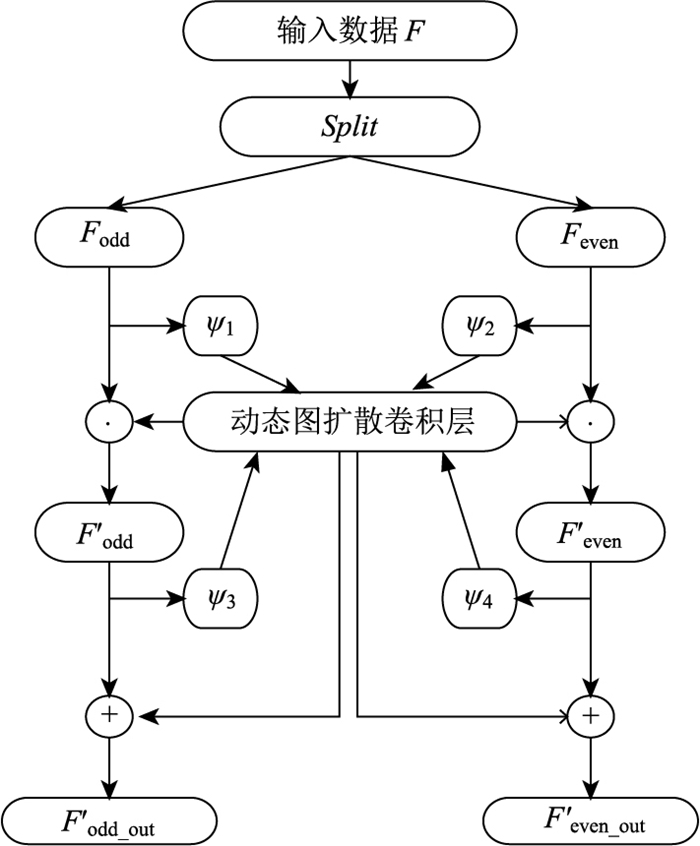
下采样卷积交互结构使得每个DSCIDG模块都具有整个序列的局部和全局信息，具体流程如图 8所示。输入序列F按时间间隔划分下采样为两个长度相等的子序列。随后，两个子序列在交互式学习结构中交互学习，共享学习各自的特征，捕获时间相关性的同时，通过嵌入在交互式学习结构中的扩散图卷积层使两个子序列能够交互学习它们各自的空间相关性。其中独立的卷积模块(ψ₁, ψ₂, ψ₃, ψ₄)提取2个子序列中独有的时间特征，将捕获空间特征的动态图扩散卷积模块嵌入其中可以共享模块中的参数权重，为防止下采样过程中的信息缺失通过交互式学习结构聚合这些时空特征，以同步挖掘复杂的时空动态特征。

图 8中，F∈$\mathbb{R}^{B \times C \times N \times T} $为交互式学习结构的输入序列，其中B为批量大小，C为特征通道数，N为节点数(路网中传感器的数量)，T为时间步长。如式(5)所示，F经序列分割函数Split得到子序列$F_{\text {odd }} \in \mathbb{R}^{B \times C \times N \times T / 2}$和$F_{\text {even }} \in \mathbb{R}^{B \times C \times N \times T / 2} 。F_{\text {odd }}$和$F_{\text {even }}$分别先经两个不同的二维卷积模块$\psi_1$和$\psi_2$以及动态图扩散卷积层进行第一次交互式学习，并与$F_{\text {even }}$和$F_{\text {odd }}$进行乘积相互作用得到$F_{\text {odd }}^{\prime} \in \mathbb{R}^{B \times C \times N \times T / 2}$和$F_{\text {even }}^{\prime} \in$ $\mathbb{R}^{B \times C \times N \times T / 2}$如式(6)~(7)所示。$F_{\text {odd }}^{\prime}$和$F_{\text {even }}^{\prime}$再进行一次交互得到最终子序列$F_{\text {odd＿out }}^{\prime} \in \mathbb{R}^{B \times C \times N \times T / 2}$和$F_{\text {even＿out }}^{\prime} \in \mathbb{R}^{B \times C \times N \times T / 2}$如式(8)~(9)所示。

$ F_{\text {odd }}, F_{\text {even }}=Split(F), $

(5)

$ F_{\text {odd }}^{\prime}=\tanh \left(G D C\left(\psi_1\left(F_{\text {even }}\right)\right)\right) F_{\text {odd }}, $

(6)

$ F_{\text {even }}^{\prime}=\tanh \left(G D C\left(\psi_2\left(F_{\text {odd }}\right)\right)\right) F_{\text {even }}, $

(7)

$ F_{\text {odd_ out }}^{\prime}=\tanh \left(G D C\left(\psi_3\left(F_{\text {even }}^{\prime}\right)\right)\right)+F_{\text {odd }}^{\prime}, $

(8)

$ F_{\text {even_out }}^{\prime}=\tanh \left(G D C\left(\psi_4\left(F_{\text {odd }}^{\prime}\right)\right)\right)+F_{\text {even }}^{\prime}, $

(9)

式中，⊙为Hadamard积，tanh为激活函数；GDC为DSCIDG中的动态图扩散卷积层；ψ₁，ψ₂，ψ₃，ψ₄为4个独立的二维卷积模块，其结构由3个卷积核大小为1×3的卷积层组成。

2.5 动态图扩散卷积层

图卷积神经网络(GCN)通过节点之间交换信息学习节点的特征表示，每个节点通过聚合其邻居节点的信息更新该节点信息，但每个节点只能捕获相邻节点的信息，而扩散图卷积^[20]在GCN中引入K阶双向随机扩散，通过随机扩散过程模拟交通流的随机性，本研究使用扩散图卷积网络替换GCN捕获交通流空间特征。此外，本研究还构建了基于节点(传感器)间连接距离的邻接矩阵A_pre和捕获交通路网动态空间依赖性的自适应邻接矩阵A_adp, 并基于这两个矩阵构造时空动态图。

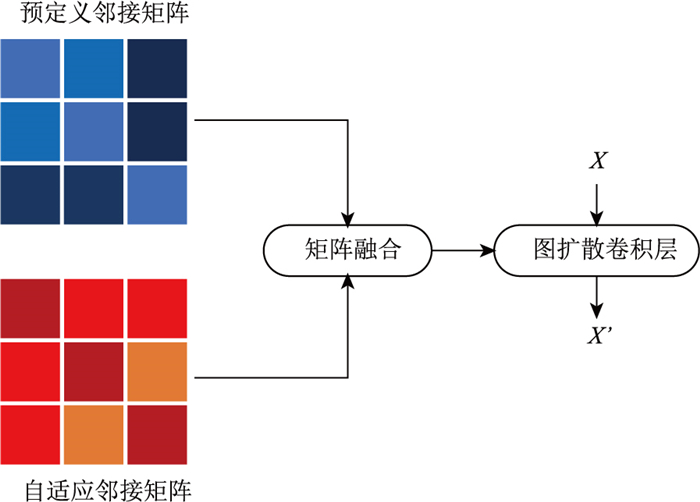
通过节点连接距离关系的预定义邻接矩阵A_pre中的各元素如式(10)所示。路网节点的动态空间依赖性难被预定义的固定图结构表示，针对该问题一些工作(Graph WaveNet^[10]、AGCRN^[11]) 采用自适应邻接矩阵来捕获空间依赖性，如式(11)所示。但这些生成方法与原始路网图结构没有关联，即忽视了预定义图结构。本研究将预定义图结构与自适应图结构相融合，并分配一个可学习的权重参数来捕获动态的空间依赖性，如式(12)所示。图扩散卷积操作定义为式(13)。矩阵融合并进行图扩散卷积的过程如图 9所示，其中$X \in \mathbb{R}^{B \times C \times N \times T} $为输入数据，$X^{\prime} \in\mathbb{R}^{B \times C \times N \times T} $为输出数据。将动态图扩散卷积层嵌于交互式学习结构，以同步捕获交通数据的同质和异构信息。

$ A_{i j}=\left\{\begin{array}{l} \exp \left[-\frac{dist\left(v_i, v_j\right)}{\sigma^2}\right], \left(v_i, v_j\right) \in E \\ \;\;\;\;\text { 且 } dist\left(v_i, v_j\right) \leqslant \lambda \\ 0, \text { otherwise } \end{array}\right. \text {, } $

(10)

式中，A_ij为矩阵A_pre中第i行第j列的元素；(ν_i, ν_j)为节点ν_i与节点ν_j的连接关系；dist (ν_i, ν_j)为节点ν_i到节点ν_j的距离；σ²为所有节点距离的方差值；$E \in \mathbb{R}^{N \times d} $为随机初始化的可学习参数；λ为阈值。

$ \boldsymbol{A}_{\text {apt }}=soft\text{max}\left(\operatorname{ReLU}\left(E E^T\right)\right)+I, $

(11)

式中，d为单个节点维度；I为单位矩阵。该设计通过ReLU激活函数消除路网中的弱连接部分，最后通过归一化得到自适应邻接矩阵。

$ \boldsymbol{A}_{\mathrm{dyn}}=\alpha \boldsymbol{A}_{\mathrm{apt}}+(1-\alpha) \boldsymbol{A}_{\mathrm{pre}}, $

(12)

$ G C N\left(X, A_{\mathrm{dyn}}\right)=\sum\limits_{k=0}^K \boldsymbol{A}_{\mathrm{dyn}}^k X \boldsymbol{W}, $

(13)

式中，α为可学习的自适应参数；$X \in \mathbb{R}^{B \times C \times N \times T} $为输入数据；K为扩散步长；$\boldsymbol{W} \in \mathbb{R}^{N \times N} $为参数矩阵。

2.6 注意力模块

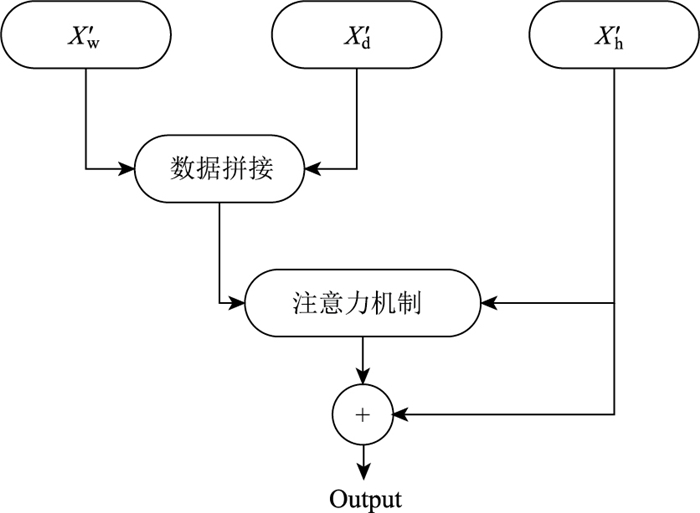
由于周期性的时间转移^[5]，周期性不能仅依赖于前几天的同一时刻。比如昨天的流量高峰出现在早上9：00，但今天的流量高峰可能由于天气等原因出现于9：10，所以用同一时刻的交通流数据进行特征融合存在缺陷，即每星期和每日的周期性并不严格，存在时间偏差。本研究通过注意力机制来解决这种偏差，如图 10所示。其中$X_{\mathrm{w}}^{\prime} \in \mathbb{R}^{B \times C \times N \times T} $, $X_{\mathrm{d}}^{\prime} \in \mathbb{R}^{B \times C \times N \times T} $，$ X_{\mathrm{h}}^{\prime} \in \mathbb{R}^{B \times C \times N \times T}$分别表示经过处理的星期、日和邻近时段的时空特征。流程为：首先将星期的周期数据和日周期数据拼接在一起得到o∈$\mathbb{R}^{B \times C \times N \times T \times 2} $，然后通过注意力机制为每个h_t(h为邻近时段的单个时间步长，总长度为T)分配一个权重w_t，通过加权和得到输出O如式(14)所示，其中w_t如式(15)所示，score函数如式(16)所示。最后通过残差连接得到输出$Output \in \mathbb{R}^{B \times C \times N \times T} $，如式(17)所示。

$ O=\sum\limits_{t=1}^T w_{\mathrm{t}} h_{\mathrm{t}}, $

(14)

$ w_{\mathrm{t}}=\frac{\exp \left(score\left(o, h_{\mathrm{t}}\right)\right)}{\sum\limits_{t=1}^T \exp \left(score\left(o, h_{\mathrm{t}}\right)\right)}, $

(15)

$ score\left(o, h_{\mathrm{t}}\right)=v \cdot \tanh \left(W_1 o+W_2 h_{\mathrm{t}}\right), $

(16)

式中v, W₁, W₂为可学习的参数。

$ Output=O+X_{\mathrm{h}}^{\prime}。$

(17)

如图 1所示，新的时空特征数据从注意力模块出来之后再次通过动态图扩散卷积层，该层的目的是对整个时空数据的特征进行校正，最后通过输出层得到预测的结果。

3 试验设计 3.1 数据集描述

试验采用交通流预测领域的通用数据集PeMS08和PeMS04。所有数据均来自加州运输局绩效测量系统^[21]，每30 s实时收集一次交通数据信息，其中包括交通流量、速度、密度等，这些数据最终汇总成5 min时间的观测，1 h有12次观测，本研究仅针对流量数据进行预测，详情如表 1所示。其中包含节点数量(传感器数量)、边数量、时间间隔、数据长度和时段。在试验中，将数据以6∶2∶2的比例划分为训练集、测试集和验证集，基于这些真实交通道路网络中传感器之间的距离构造图的邻接矩阵并采用Z-Score方法进行数据标准化处理。

3.2 试验参数设置

在试验中，采用Pytorch深度学习框架对模型进行实现，用过去1 h的12个连续时间切片数据预测未来1 h共12个连续时间切片数据。试验环境为15 vCPU Intel(R) Xeon(R) Platinum 8338C CPU @ 2.60 GHz和NVIDIA RTX 3090(24 GB)GPU。为避免随机性，在数据集上使用PyTorch深度学习框架运行模型进行10次评估。

训练过程中批次大小设置为64，epoch设置为500，学习率设置为0.001，初始1×1卷积升维通道数为64，扩散步长K固定为2，优化器为Adam。为防止模型过拟合，采用Early Stopping进行训练，模型在410个epochs左右达到收敛终点。

3.3 基线模型

选用部分经典和前沿交通流预测模型与本研究模型进行对比分析。具体为：传统的数学统计模型HA和机器学习模型、循环神经网络GRU模型和使用因果卷积的TCN模型、构建扩散过程的DCRNN模型、堆叠两个时空卷积模块的STGCN模型、结合自适应邻接矩阵与因果卷积的GWN模型、结合自适应图与GRU的AGCRN模型、基于注意力机制和图卷积的ASTGCN模型、构造局部时空图的STSGCN模型、结合扩散图卷积与时空同步机制STIDGCN模型和考虑时空相似性的STS-DGCN模型。

3.4 模型评价指标

选用3个标准指标来作为试验验证评价指标验证模型有效性: 平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方根误差(RMSE)，分别记为e_MA, e_MAP, e_RMS具体计算公式如下：

$ e_{\mathrm{MA}}=\frac{1}{N} \sum\limits_{i=1}^N\left|y_i-\overline{y_i}\right|, $

(18)

$ e_{\mathrm{MAP}}=\frac{100 \%}{N} \sum\limits_{i=1}^N \frac{\left|y_i-\overline{y_i}\right|}{y_i}, $

(19)

$ e_{\mathrm{RMS}}=\sqrt{\frac{1}{N} \sum\limits_{\text{i}=1}^N\left(y_i-\overline{y_i}\right)^2}, $

(20)

式中，N为样本个数；y_i为真实值；$\overline{y_i} $为预测值。

3.5 试验结果与分析 3.5.1 模型预测性能

基线模型与本研究模型在两个数据集上预测未来1 h(12个值)的平均性能如表 2所示。在3个评价指标中，本研究模型(MDDGCNN)性能均取得最优结果。传统统计模型HA难捕获非线性特征，其结果最差。相比之下，SVR这种机器学习方法对非线性特征的捕获能力使预测性能获得提升。在深度学习模型中，TCN比GRU捕获时间依赖性的能力更强。但上述模型仅考虑交通流数据的时间依赖性，没有考虑空间依赖性。因此，STGCN和DCRNN所代表的时空GCN模型具有较好的性能，这说明图结构有助于挖掘交通路网中的复杂时空关系从而提示模型性能。而相比于固定图结构，采用动态图结构的GWN，STIDGCN和AGCRN模型有更佳的性能，这也说明动态图更适应交通流动态时空变化的特性，对提高预测精度具有重要作用。由于注意力机制捕获长序列时间相关性的优势，基于注意力机制的模型ASTGCN也具有出色的性能。此外，考虑时空相似性的STS-DGCN具有良好的预测结果也表明交通流数据在时空维度上具有高度的相似性。

本研究模型在数据集PeMS08和PeMS04的3个指标上均优于基线模型。这表明：多时间尺度的输入数据能反映时间相似性，有助于挖掘不同时段的时空特性；注意力机制可解决周期性扰动问题，从而提升模型学习能力；下采样卷积与交互式学习策略相结合，能同时把握交通流时间序列的局部和全局特征；预定义图结构与自适应图结构的融合，可捕获动态空间依赖性；在交互式学习结构中嵌入动态图扩散卷积层，能够同步捕获交通路网的动态时空特征，加强序列间的相互作用，进而更好地挖掘交通流数据中的复杂时空相关性。

选择ASTGCN，STSGCN，AGCRN和STIDGCN这4个预测性能较好的模型与本研究模型在不同时间步下的预测性能进行对比分析，预测结果如图 11所示。由图可知，随着时间步长增加模型的预测误差值均有所提高。模型MDDGCNN在3个评价指标上不同预测步长下均优于对比模型且增长幅度不大，验证了所建模型不同预测时长下的一致优越性。

3.5.2 消融试验分析

为进一步评估预测模型中各组件的有效性，在PeMS08数据集上对MDDGCNN模型与如下变体模型进行比较分析，如表 3所示。(1)MDDGCNN-H模型：仅使用邻近时间段的数据作为输入的模型。(2)MDDGCNN-D：移除自适应邻接矩阵使用预定义邻接矩阵的模型。(3)MDDGCNN-S：单独捕获时空特征，将嵌入于交互式结构中的图卷积层置于交互式结构之后的模型。(4)MDDGCNN-R：不使用交互式学习结构的模型。(5)MDDGCNN-C：不使用两个1×3的卷积核替代一个1×5的卷积核的模型(SCINet中卷积模块由大小为1×5卷积核与1×3卷积核的卷积层组成)。

上述试验表明：(1)多时间尺度能获得更多维的时间特征从而提高模型性能。(2)自适应邻接矩阵能捕获复杂的动态空间依赖提高模型效能。(3)同步捕获时空特征能有效捕获时空网络中的异质性。(4)交互式学习结构处理具有长期依赖关系和复杂结构的时间序列数据更有优势。(5)堆叠小尺寸卷积核的卷积层比单个大尺寸的卷积核的卷积层能在保证感受野不变的同时使非线性表达能力更强(非线性函数增加)，并在一定程度上提升网络效果并减少计算量和参数量。

3.5.3 结构配置分析

下采样卷积交互动态图结构(DCIDG)由4个独立的卷积模块和一个权重共享的动态图扩散卷积模块组成。为验证交互式学习结构当前组件配置的合理性，对其结构配置进行修改并进行对比试验分析，如表 4所示。(1)DCIDG-Convx1结构：将4个独立的卷积模块替换为一个共享权重的卷积模块结构。(2)DCIDG-Ix1结构：交互式学习结构中的交互式学习次数由2次变为1次(去掉2个卷积模块和减少1次图卷积运算的结构。(3)DCIDG-Ix4结构：交互式学习结构中的交互式学习次数由两次变为4次结构。(4)DCIDG-Gx2结构：将权重共享的动态图扩散卷积模块替换为两个独立的动态图扩散卷积模块的结构，不同配置下多时间步长下的模型性能如图 12所示。

上述试验表明：相比于权重共享卷积模块，独立卷积模块局部特征捕获能力更强；反之，相比于独立的动态图扩散卷积模块，权重共享图扩散卷积模块使节点间关系更紧密，因此相比于时间维度，空间维度上使用权重共享模块使模型性能更好。MDDGCNN通过交互式学习策略同步捕获时空特征，因而减少交互式学习次数将导致模型时空特征捕获能力下降。然而，试验表明2次交互式学习足以拟合特征，增加交互式学习次数会导致模型特征拟合能力下降。

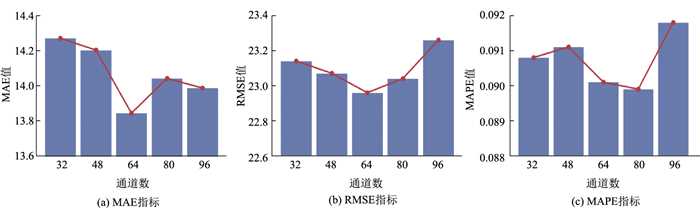
3.5.4 超参数分析

本研究模型并未进行模块堆叠，因此与模型结构相关的超参数是1×1卷积升维的特征通道数。为保证模型学习足够的特征，又不过多地增加模型的参数和计算量，对其特征通道数选取进行对比试验分析，如图 13所示。

上述试验表明：特征通道数对模型性能会产生影响。在3个指标中，MDDGCNN的性能并未随着特征通道数的增加而提高，并在MAE指标和RMSE指标中，通道数为64时模型具有较优的性能，在MAPE指标中通道数为80时模型具有更优的性能。但随着特征通道数增加会导致计算量和过拟合风险的提高。综合上述情况，最终选择MDDGCNN的模型特征通道数为64。

4 结论

本研究针对交通流预测精度低的问题提出一种基于多尺度下采样卷积交互的动态图卷积交通流预测方法。该方法在PeMS08和PeMS04两个公开数据集上均优于目前较为先进的交通流预测模型。得出以下主要结论：(1)基于交通流数据的特性引入周期性数据有助于多维度的时间相关性。(2)构建适用于图扩散卷积神经网络的动态图结构有助于挖掘交通流数据的动态空间相关性。(3)将动态图结构嵌入到下采样-卷积-交互结构中进行时空特征同步捕获助于挖掘隐藏的时空特性。由于交通拓扑图上的一些节点(如传感器)可能存在少量缺失和损坏导致图结构不完整，动态图生成技术在研究中有广泛的应用空间。此外，除了考虑上一日和上一周同时段的时间相似性也能聚合前日和上上周等更多的相似特征。因此，在未来的工作中应考虑图卷积中节点数量的变化以优化动态图的表达能力和多范围的时间相似性从而提高模型的适应能力。