扩展功能
文章信息
- 宁杰钧, 罗资清, 骆俊晖, 尹世平, 刘子瑞.
- NING Jiejun, LUO Ziqing, LUO Junhui, YIN Shiping, LIU Zirui
- TRC复合CFRP筋加固RC梁正截面承载性能
- Normal section bearing capacity of RC beams reinforced with TRC and CFRP bars
- 公路交通科技, 2025, 42(8): 148-157
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(8): 148-157
- 10.3969/j.issn.1002-0268.2025.08.016
-
文章历史
- 收稿日期: 2023-04-06
2. 中国矿业大学 江苏省土木工程灾变与智能防控高校重点实验室, 江苏 徐州 221116;
3. 中国矿业大学 深地工程智能建造与健康运维全国重点实验室, 江苏 徐州 221116
2. Jiangsu Key Laboratory of Disaster Impact and Intelligent Prevention in Civil Engineering, China University of Mining and Technology, Xuzhou, Jiangsu 221116, China;
3. State Key Laboratory of Intelligent Construction and Healthy Operation and Maintenance of Deep Underground Engineering, China University of Mining and Technology, Xuzhou, Jiangsu 221116, China
作为交通网络的关键节点,桥梁的性能直接关系到国家运输效率和经济活力。中国地域广阔,地质与气候条件复杂,许多桥梁长期暴露于恶劣环境,遭受严重侵蚀[1-2]。同时,旧桥因服役时间增长、超载等问题,其设计承载力已难以满足现行标准和交通需求,导致病害频发,甚至成为危桥,安全隐患突出[3-4]。这不仅威胁到公众的生命财产安全,也对交通可持续发展构成挑战。因此,对大量危旧桥梁进行科学处治刻不容缓。通过加固手段提升其耐久性和安全性,延长使用寿命,是缓解交通压力、节约重建资金的有效途径。
织物增强混凝土(Textile Reinforced Concrete,TRC)材料是一种兼具良好力学性能、抗渗、抗碳化和抗冻融性能的新型结构修复材料[5-8],结合纤维增强复合材料(Fiber Reinforced Polymer,FRP)植筋技术,可充分发挥FRP筋的轻质高强与耐腐蚀特性[9-10],有效改善既有钢筋混凝土(Reinforced Concrete,RC)桥梁的开裂、过度变形和承载能力不足,同时综合提升了结构的耐久性。
回顾已往研究,Eljufout[11]以加固后的RC梁为参考试件,在等幅循环应力作用下进行疲劳试验。随后对试件进行NSM-CFRP加固修复,并在与参考试件相同的循环荷载下进行试验。修复后的钢筋混凝土梁的疲劳响应较加固前有明显改善。Haddad[12]研究了表面嵌贴(NSM)碳纤维增强聚合物(CFRP)增强混凝土梁的弯曲性能和破坏模式,研究发现,当NSM-CFRP条带沿横向与主筋保持适当间距布置时,能有效避免端部盖层剥离现象,该加固方式对构件韧性及残余抗弯性能具有增强作用,但会导致加固梁延性的下降。姚杰[13]分别用CFRP筋和BFRP筋嵌入式加固预制裂缝的混凝土梁,比较了2种FRP筋加固效果, 结果表明BFRP筋较CFRP筋加固的梁的极限荷载高。Kamani[14]通过四点弯曲试验研究了配网率、开裂后强化系数和水泥在纤维内的渗透性对梁弯曲性能的影响,提出了加固梁的极限抗弯承载力与纤维性能指标(FPI)间的关系。针对TRC加固RC梁的弯曲力学特性,尹世平[15]和徐世烺[16]结合RC结构抗弯设计原理,系统地构建了纤维编织网与钢筋协同增强混凝土受弯构件的计算模型;进一步,尹世平[17-19]探明了氯盐环境下加固构件的耐久性演变规律,提出了新边界条件下TRC层中氯化物扩散方程,以及TRC加固梁在氯盐侵蚀下极限抗弯承载力的计算公式。盛杰[20-22]研究了TRC厚度、钢筋直径、纤维编织网层数等因素对TRC加固RC梁中钢筋起锈时间和加固梁受弯承载力的影响规律,结果表明在海洋大气腐蚀环境下,TRC加固RC梁的抗弯承载能力随侵蚀时间延长呈非线性衰减特征,但是其劣化速率显著低于普通RC梁。增大TRC加固层厚度既可延缓钢筋锈蚀的发生,又能有效抑制承载力衰减进程;钢筋直径与起锈时间无明显相关性,对裂缝萌生时间的显著性影响也较为有限[23]。
综上,FRP嵌入式加固和TRC加固后的梁抗弯性能在不同环境下有着不同程度的提升,但NSM-CFRP加固和TRC加固分别受梁底尺寸和加固层数的限制。将2种材料复合起来可以弥补加固量受限的问题,提升加固梁力学性能。TRC加固可以有效提高RC梁的耐久性能;NSM-CFRP加固则可以有效增强RC梁的抗疲劳能力;复合加固方法通过整合不同材料的优势特性,形成协同增强效应。当前关于加固构件的研究主要集中在单一材料加固,关于复合加固对梁抗弯性能的影响还鲜有研究成果。由于复合加固可充分发挥不同材料间的优势,弥补单一材料带来的不足,因此有必要对复合加固后梁的抗弯性能进行研究。本研究共设计4组试验梁,探究预应力施加状态和不同加固方式对梁抗弯性能的影响,并基于试验数据,尝试建立复合加固梁承载力计算公式,进而预测其极限承载能力,为TRC复合嵌入式CFRP筋加固RC梁的进一步研究奠定基础。
1 试验概况 1.1 材料性能(1) 混凝土
设计试验梁所用混凝土强度等级为C40,实测150 mm的立方体试块平均抗压强度为46.34 MPa。
(2) 细粒混凝土
试验TRC基体采用细粒混凝土,其配合比参照文献[19],如表 1所示。通过试验测得细粒混凝土28 d抗压强度平均值为52.7 MPa。
| 水泥 | 细砂 | 粗砂 | 粉煤灰 | 硅灰 | 减水剂 | 水 |
| 475 | 460 | 920 | 168 | 35 | 9.1 | 262 |
(3) 钢筋
试验梁采用的受拉纵筋屈服强度为546 MPa,极限抗拉强度为639 MPa。
(4) CFRP筋
CFRP筋力学性能如表 2所示。
| 拉伸模量/GPa | 拉伸强度/MPa | 伸长量/% |
| 121 | 2 015.9 | 1.7 |
(5) 纤维编织网
纤维编织网由玻璃纤维束和碳纤维束编织而成。玻璃纤维束主要起固定作用,而碳纤维束起增强作用,经纬两向相邻纤维束间距为10 mm,网格有效截面积为0.45 mm2,纤维编织网各项参数如表 3所示。
| 纤维类型 | 每束纤维数量/根 | 单丝纤维断裂伸长/ % | 单丝纤维弹性模量/ GPa | 单丝纤维抗拉强度/ MPa |
| T700S | 12 000 | 2.0 | 231 | 4 660 |
| E-glass | 4 000 | 4.5 | 65 | 3 200 |
1.2 试件设计与制作
不同的钢筋配筋率会影响梁的破坏形态和承载力等指标,试验梁在加固前均设计为适筋梁,且梁配筋率均为0.37%。本次试验共设计4根梁,其几何参数和配筋构造均保持一致,如图 1所示。其中,梁有效跨度为1 600 mm,混凝土保护层厚度取20 mm,剪跨段箍筋按80 mm间距布置,纯弯区箍筋间距为200 mm以降低箍筋约束效应。试件编号及加固参数如表 4所示。

|
| 图 1 复合加固梁配筋及截面示意图(单位:mm) Fig. 1 Schematic diagrams of reinforcement and cross- section of composite reinforced beam (unit: mm) |
| |
| 编号 | 名称 | 开槽尺寸 | CFRP配筋率/% | 槽间净距/ mm | 预应力/ kN |
| L1 | 对照梁 | — | — | — | — |
| L2 | TRC加固梁 | — | — | — | — |
| L3 | 复合加固梁 | 2db×2db | 0.13 | 40 | 0 |
| L4 | 预应力复合加固梁 | 2db×2db | 0.13 | 40 | 20×2 |
| 注:db为CFRP筋直径;预应力中20×2表示在梁底植入的CFRP筋材数量为2根,单根紧预应力张拉值为20 kN。 | |||||
加固工艺流程关键工序为:(1)采用开槽机沿梁底顺直开槽;(2)利用除尘设备清理槽内灰尘;(3)向槽内注入黏结剂至开槽深度的1/2,随后在槽正中心放入CFRP筋; (4)在端部用夹具对CFRP筋进行锚固后张拉;(5)26 ℃恒温条件下标准养护72 h,待植筋胶达到要求强度后解除锚固,预留一定的硬化时间开始TRC加固层施工;(6)梁底混凝土表面进行凿毛处理至粗骨料外露;(7)涂抹细粒混凝土并铺设纤维编织网;(8)表面精细找平后,在室温下养护28 d,至此加固完毕,TRC加固试件的加固层数均为1层。
1.3 试件分组与加载方案试验以加固方式和有无预应力作为研究变量,研究在不同因素下加固梁的破坏模式、裂缝分布情况、极限承载力及各测点的应变规律,试验分组如表 4所示。
试验加载装置图中,加载系统采用50 t的液压千斤顶,将50 t量程的压力传感器放置在分配梁与千斤顶顶推端。首先进行预加载, 为消除试件与支座间的间隙,以5 kN荷载水平加载并持载100 s,随后分级卸载至零载状态。然后正式加载。试验采用分级加载模式,其中对照梁分级级差为2 kN,复合加固梁则为5 kN,且每级加载后持载3~5 min。为确保荷载与裂缝等的精准测量与观测,在临近各临界状态时,缩小每级级差。临近破坏时及时撤除位移计等仪器,防止因试件变形过大导致仪器损坏,待卸载后记录最终破坏形态。
2 试验结果分析 2.1 破坏形态分析试件L1呈现适筋破坏模式,即受拉钢筋首先退出工作,随后受压区混凝土被压溃。试件L2在初始加载阶段纯弯段首先产生裂缝;随着荷载递增,梁底部裂纹数量持续增加并向上延伸;受拉钢筋屈服后,碳纤维束部分拉断并伴随有断裂声;随着荷载的进一步增大,裂缝宽度增速显著提升而新生裂缝数量趋缓,主裂缝出现,随后碳纤维被全部撕裂,上部受压区混凝土被压碎。预应力复合梁和非预应力复合加固梁失效模式具有相似性,试件L3在初始受力阶段,试验梁纯弯段率先出现裂缝并伴有界面胶层断裂声;随着纵筋屈服,碳纤维发生断裂并伴有明显的断裂声;裂缝数量随加载继续增速逐渐放缓,但宽度显著增加,最终CFRP筋与纤维编织网均发生断裂并发出剧烈响声,且TRC未出现剥离现象。
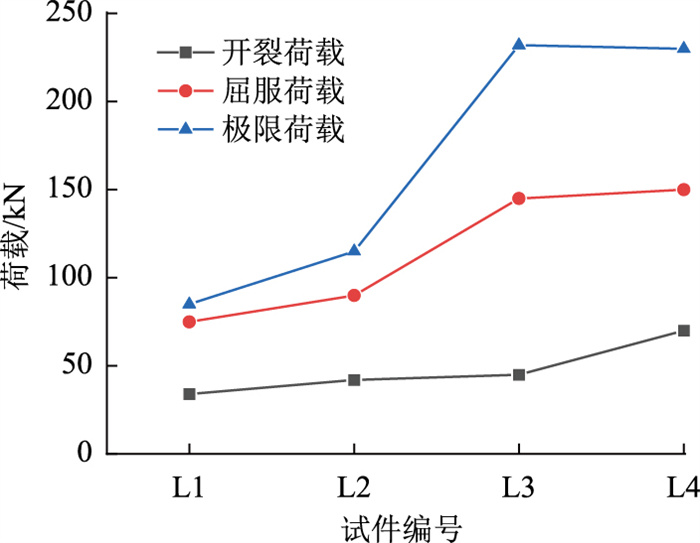
2.2 承载力分析不同加固方式下的荷载对比如图 2所示,采用嵌入式复合加固法后,未施加预应力的复合加固试验梁较未加固试验梁开裂荷载提升了32.35%,施加预应力的复合加固试验梁较未加固试验梁开裂荷载提高了135.29%,较未施加预应力的复合加固试验梁开裂荷载提升了77.78%。可见预应力对开裂荷载提高显著,复合加固试验梁屈服荷载和极限荷载均提升明显,极限承载力较未加固试验梁和TRC加固试验梁分别提升了170.58%和100%。这是由于加载初期,嵌入梁底混凝土内碳纤维筋和梁底部的纤维编制网可以限制混凝土的应变,延缓混凝土开裂,从而一定程度上提高了加固梁的开裂荷载。对于施加预应力的碳纤维筋,其放张后对梁下部的预压力进一步提高了梁的开裂荷载。
|
| 图 2 不同加固方式下的荷载对比 Fig. 2 Comparison of loads with different reinforcement methods |
| |
混凝土开裂后,碳纤维筋和纤维编织网承担了一部分梁底混凝土所受拉力,进一步发挥了碳纤维筋和纤维编织网的作用。受拉区拉力随着荷载的增加而不断增大,但由于碳纤维筋有较大的纵向刚度,对裂缝的开展有较好的限制作用,从而延缓了中和轴的向上移动,通过增大受压区混凝土的面积来平衡下部拉力。这不但使混凝土较高的抗压性能得到充分利用,还有效提高了梁的极限承载力。在加载后期,尤其是钢筋屈服以后,碳纤维筋起到了重要作用,其优异的抗拉性能得到了充分的发挥。
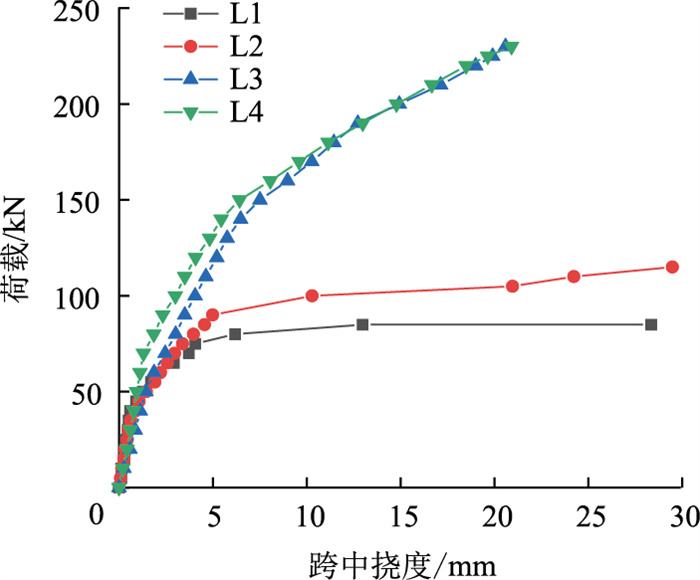
2.3 荷载-挠度分析试验梁的荷载与跨中挠度关系如图 3所示。由图可见,TRC复合碳纤维筋加固能有效提高梁的刚度,施加的力相同时,复合加固梁的跨中挠度较其他梁更小;在梁开裂前,各试验梁的跨中挠度相近且较小;梁开裂后,特别是钢筋屈服后,未加固梁跨中挠度增加十分明显,而加固梁跨中挠度增加速率较小,且随着荷载的增加这种差异有所增大,其中仅TRC加固的梁刚度较未加固梁有小幅提升,但提升明显小于复合加固梁。施加预应力的复合加固梁在加载前中期较未施加预应力的复合加固梁曲线斜率更大,刚度提升更明显,中后期曲线接近重合,提升效果相当。这是由于在梁底部植入碳纤维筋实际上相当于增加了梁受拉钢筋的配筋率,并且碳纤维筋可以有效抑制裂缝的发展,而施加了预应力的碳纤维筋对裂缝发展的抑制效果更好。因此在加载中期,特别是下部受拉钢筋屈服以后,碳纤维筋对梁抗弯刚度的提升更为明显。
|
| 图 3 试验梁的荷载与跨中挠度关系 Fig. 3 Relation between load and mid-span deflection of test beams |
| |
2.4 裂缝分布分析
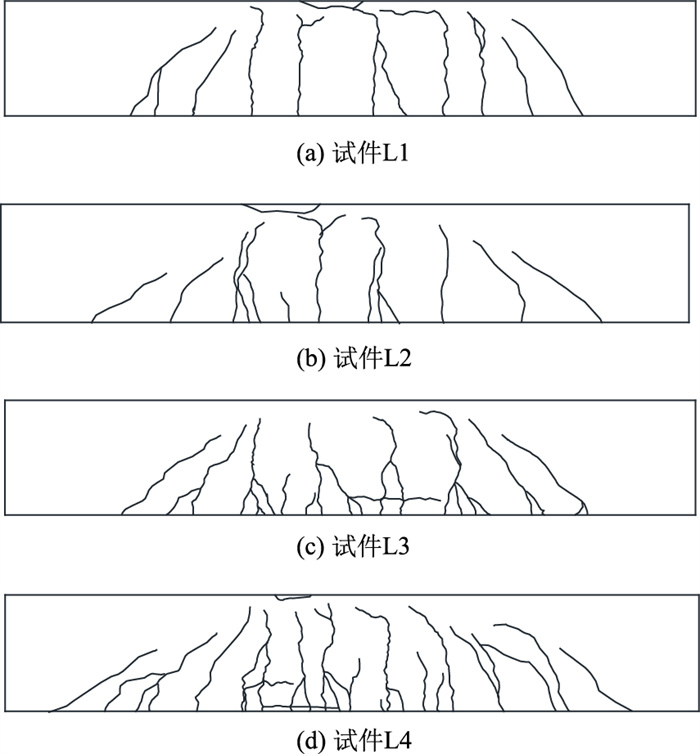
各试件裂缝分布如图 4所示。由图可见,TRC加固梁纯弯曲区段裂缝分布密度相对较低,裂缝间距在100 mm左右,而复合加固试件则相反,其间距在35 mm左右。因此,复合加固对裂缝数量和间距的改善明显优于单一TRC加固。对比试件L3和试件L4的裂缝分布图可以看出,预应力复合加固梁较无预应力复合加固梁纯弯段的裂缝数量略多,裂缝间距略小。由此可见,预应力的应用可以进一步增加梁纯弯段裂缝的数量,减小裂缝间距。
|
| 图 4 裂缝分布图 Fig. 4 Schematic diagrams of fracture distribution |
| |
2.5 裂缝宽度分析
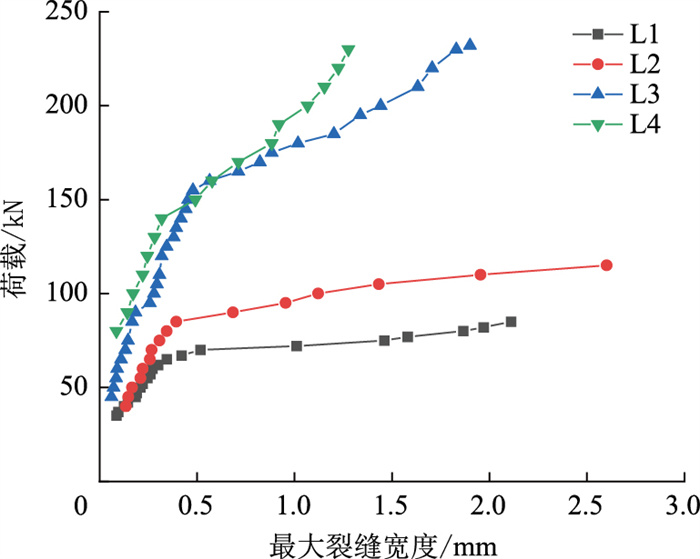
各试件的最大裂缝宽度如图 5所示。TRC加固和复合加固都对裂缝宽度的抑制有影响,复合加固抑制裂缝发展的效果更显著,预应力的施加可以有效抑制裂缝发展。L2和L3在0.3Mu(Mu为极限弯矩)下的最大裂缝宽度相比于L1分别降低了20.1%和66.84%;与L3相比,L4在0.3Mu下的最大裂缝宽度降低了41.1%。这是因为TRC加固和复合加固均提高了梁的抗弯刚度,纤维编制网的碳纤维和CFRP筋限制了梁的变形和裂缝发展,从而减小裂缝宽度。预应力的施加进一步增大了梁的刚度,更充分利用了CFRP筋较高的抗拉强度,更好地限制了裂缝的开展,减小了裂缝宽度。
|
| 图 5 各试件的最大裂缝宽度 Fig. 5 Maximum crack widths of specimens |
| |
2.6 荷载-应变分析 2.6.1 钢筋应变分析
试验梁在各级荷载下的钢筋应变发展规律如图 6所示。应变曲线呈现典型的3阶段特征,分别对应构件开裂前阶段、钢筋屈服前阶段及破坏临界阶段。开裂前各试验梁钢筋应变与应力呈线性比例关系,各曲线斜率相近。试件开裂后阶段应变增速显著高于开裂前水平,该差异特征在所有试验组呈现一致性规律。当未加固梁发生开裂后,曲线斜率降至最低值,当荷载达到75 kN时,下部受拉钢筋屈服,钢筋应变曲线趋于平缓,随后迅速进入破坏阶段。

|
| 图 6 钢筋应变曲线 Fig. 6 Rebar strain curves |
| |
对于L2,由于纤维编织网对构件变形的抑制作用,加载后期,在相同荷载下钢筋的应变低于L1,加载前期钢筋应变接近,原因可能是纤维编织网受力存在滞后性,梁有一定的变形后纤维编制网才开始发挥作用。
L3较L1开裂后应变增长速率较慢,斜率较大,在下部受拉钢筋屈服后,由于CFRP筋和纤维编织网共同承担抑制构件的变形的作用,直至纤维编织网和CFRP筋被拉断,因而试验梁的极限承载力提高明显。
对比L4和L3可以发现,L4的曲线斜率更大,这表明预应力能够有效缓解受拉区钢筋应变的增长速率,原因可能是预应力CFRP筋能承担更多的荷载,从而使钢筋承担的荷载减小。
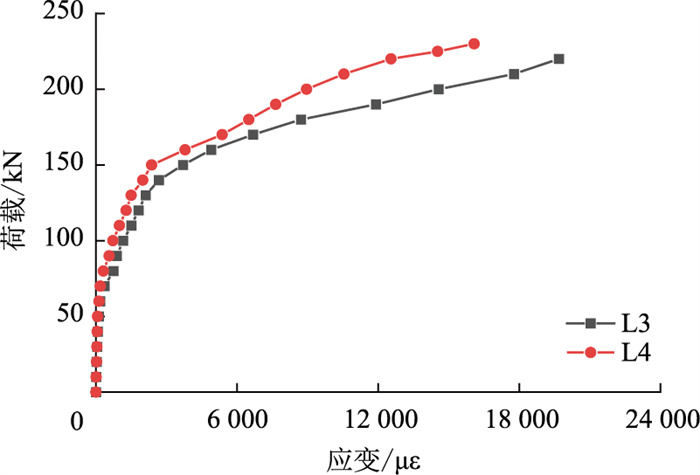
2.6.2 CFRP筋应变分析复合加固梁碳纤维筋荷载-应变曲线如图 7所示。由图可见,钢筋与CFRP筋应变分布趋势具有相似性,梁开裂之前,2条曲线几乎重合,且其斜率也大致相同。梁开裂之后,施加了预应力的复合加固梁L4的碳纤维筋应变值较未施加预应力的加固梁L3小。这可能是因为在梁开裂后,未施加预应力的加固梁对梁变形的限制作用小于施加预应力的加固梁,因此未施加预应力的加固梁的应变发展就更加显著,同时也印证了预应力的施加可以有效地抑制构件中CFRP的应变增长。
|
| 图 7 CFRP筋荷载-应变曲线 Fig. 7 Load-strain curves of CFRP bar |
| |
2.6.3 截面应变分析
复合加固梁与预应力复合加固梁在跨中梁截面高度上的应变分布特征如图 8所示。复合加固梁跨中截面混凝土应变梯度在加载过程中呈线性变化规律,较好地满足了平截面假定。中性轴位置随荷载的持续增加沿梁高方向逐渐上移。

|
| 图 8 跨中截面应变 Fig. 8 Strain of middle-span section |
| |
3 TRC复合嵌入式CFRP加固钢筋混凝土梁承载力计算 3.1 基本假定
(1) 试件梁跨中截面的混凝土应变分布满足平截面假定。
(2) 假定细粒混凝土-梁混凝土界面、CFRP筋-结构胶界面及结构胶-混凝土界面这3个界面均无相对滑移。
(3) 开裂后忽略混凝土抗拉强度对梁的贡献。
(4) 采用《混凝土结构设计标准》 (GB/T 50010—2010)建议的混凝土材料的应力-应变关系式。
(5) 假定复合纤维材料的本构模型为线弹性模型,其拉应力等于弹性模量与拉应变的乘积。
3.2 破坏模式判定最优配网率可由平衡破坏时力的平衡方程求得:
| $ \begin{equation*} \rho_{\mathrm{ot}}=\frac{\alpha_{1} \beta_{1} f_{\mathrm{c}} x_{0}-f_{\mathrm{y}} h_{0} \rho_{\mathrm{s}}-f_{\mathrm{fu}} h \rho_{\mathrm{f}}}{m \sigma_{\mathrm{tu}} t}, \end{equation*} $ | (1) |
式中,ρot为最优配网率;ρt为纤维编织网配网率;ρs为钢筋配筋率;α1为混凝土轴心抗压强度设计值折减系数;β1为等效矩形应力图高度系数;x0为中心轴高度;fc为混凝土轴心抗压强度设计值;fy为钢筋极限抗拉强度;h0为梁截面有效高度;ffu为CFRP筋极限抗拉强度;h为截面高度;m为纤维编织网修正系数;t为加固层厚度;σtu为纤维编织网碳纤维束极限抗拉强度。
可联立变形协调方程和式(1)确定最优配网率,加固梁破坏模式为:(1)受压破坏,实际配网率超过最优值时发生;(2)平衡破坏,实际配网率等于最优值时发生;(3)受拉破坏,实际配网率低于该最优值时出现。
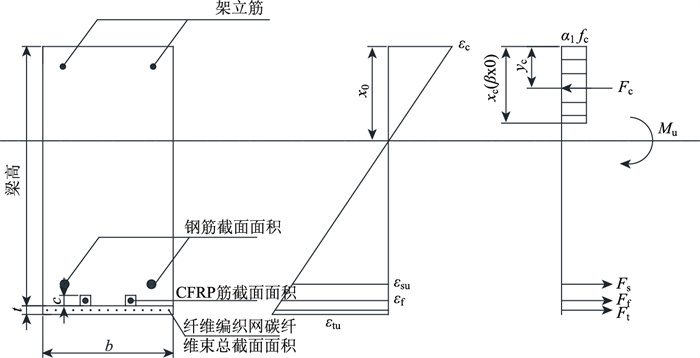
3.3 承载力计算 3.3.1 受拉破坏受拉破坏时复合加固梁截面应力应变如图 9所示。通过结合变形协调条件与静力平衡方程,基于加固RC梁的结构计算简图求得混凝土受压区高度,受拉破坏时中性轴高度x0计算为:
| $ \begin{equation*} \int_{0}^{x_{0}} \sigma_{\mathrm{c}} \varepsilon_{\mathrm{c}} b \mathrm{~d} y=f_{\mathrm{y}} A_{\mathrm{s}}+f_{\mathrm{fu}} A_{\mathrm{f}}+\sigma_{\mathrm{tu}} A_{\mathrm{t}}, \end{equation*} $ | (2) |
|
| 图 9 受拉破坏时复合加固梁截面应力应变图 Fig. 9 Stress-strain diagram of cross-section of composite reinforced beam under tensile failure 注:b为梁面宽度; c为开槽深度; εc为混凝土应变; εsu为钢筋极限应变; εf为CFRP筋应变;εtu为纤维编织网极限应变;Fc为受压区混凝土合力;Fs为受拉钢筋合力;Ff为CFRP筋合力;Ft为纤维编织网碳纤维束合力;Mu为极限弯矩。 |
| |
式中,σ为混凝土应力;As为钢筋截面面积;A6为纤维束总截面面积;At为纤维束总截面面积;Af为CFRP筋截面面积。
联立变形协调方程和混凝土本构模型可得:
| $ \left\{\begin{array}{ll} A_{1} x_{0}^{3}+B_{1} x_{0}^{2}+C_{1} x_{0}+D_{1}=0 & \left(0 \leqslant \varepsilon_{\mathrm{c}} \leqslant \varepsilon_{0}\right) \\ A_{1}^{\prime} x_{0}^{2}+B_{1}^{\prime} x_{0}+C_{1}^{\prime}=0 & \left(\varepsilon_{0} \leqslant \varepsilon_{\mathrm{c}} \leqslant \varepsilon_{\mathrm{c}}\right) \end{array}, \right. $ | (3) |
式中,A,B,C,D均为系数;ε0为混凝土的峰值压应变。
受压区混凝土合力至其边缘的距离yc可由x0代入式(4)求得。极限弯矩如式(5)所示。
| $ y_{\mathrm{c}}=\left\{\begin{array}{ll} \frac{4 \varepsilon_{0}-\varepsilon_{\mathrm{c}}}{4\left(3 \varepsilon_{0}-\varepsilon_{\mathrm{c}}\right)} x_{0} & \left(0 \leqslant \varepsilon_{\mathrm{c}} \leqslant \varepsilon_{0}\right) \\ \left(1-\frac{3-\varepsilon_{0}^{2} / 2 \varepsilon_{\mathrm{c}}^{2}}{6-2 \varepsilon_{0} / \varepsilon_{\mathrm{c}}}\right) x_{0} & \left(\varepsilon_{0} \leqslant \varepsilon_{\mathrm{c}} \leqslant \varepsilon_{\mathrm{c}}\right) \end{array}, \right. $ | (4) |
| $ \begin{equation*} M_{\mathrm{u}}=\alpha_{1} \beta_{1} f_{\mathrm{c}} b x_{0}\left(h-\frac{c}{2}-y_{\mathrm{c}}\right) \circ \end{equation*} $ | (5) |
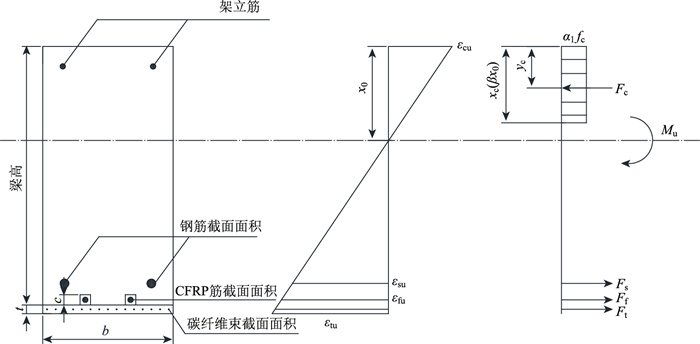
平衡破坏时复合加固梁截面应力应变图如图 10所示。平衡破坏时中性轴高度x0计算为:
| $ \begin{equation*} \alpha_{1} \beta_{1} f_{\mathrm{c}} b x_{0}=f_{\mathrm{y}} A_{\mathrm{s}}+f_{\mathrm{fu}} A_{\mathrm{f}}+\sigma_{\mathrm{tu}} A_{t} 。\end{equation*} $ | (6) |
|
| 图 10 平衡破坏时复合加固梁截面应力应变图 Fig. 10 Stress-strain diagram of cross-section of composite reinforced beam under equilibrium failure 注:εcu为混凝土极限应变;εfu为CFRP筋极限应变。 |
| |
复合加固梁的极限弯矩为:
| $ \begin{equation*} M_{\mathrm{u}}=\alpha_{1} \beta_{1} f_{\mathrm{c}} b x_{0}\left(h-\frac{c}{2}-\frac{x_{0}}{2}\right) 。\end{equation*} $ | (7) |
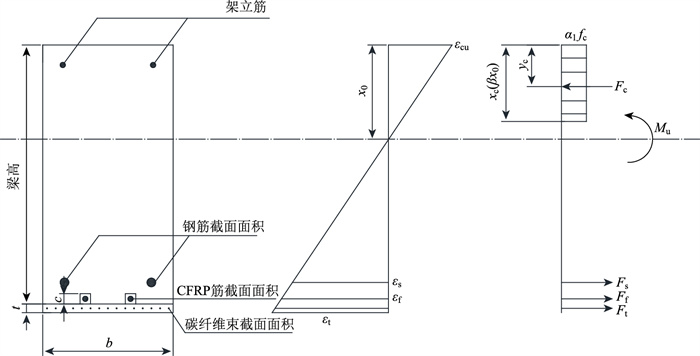
受压破坏时复合加固梁截面应力应变如图 11所示。
|
| 图 11 受压破坏时复合加固梁截面应力应变图 Fig. 11 Stress-strain diagram of cross-section of composite reinforced beam under compressive failure |
| |
受压破坏时中性轴高度x0的计算为:
| $ \begin{equation*} \alpha_{1} \beta_{1} f_{\mathrm{c}} b x_{0}=f_{\mathrm{y}} A_{\mathrm{s}}+\varepsilon_{\mathrm{f}} E_{\mathrm{f}} A_{\mathrm{f}}+\sigma_{\mathrm{tu}} A_{\mathrm{t}}, \end{equation*} $ | (8) |
联立式(8)和变形协调方程可求得x0。极限弯矩为:
| $ \begin{equation*} M_{\mathrm{u}}=\alpha_{1} \beta_{1} f_{\mathrm{c}} b x_{0}\left(h-\frac{c}{2}-\frac{x_{0}}{2}\right) 。\end{equation*} $ | (9) |
加固梁抗弯极限承载力数据对比如表 5所示。复合加固梁极限抗弯承载力理论计算值与实际测量值偏差较小,其误差范围均不超过10%。这验证了采用截面分析法建立的承载力预测模型具有较好的适用性。
| 试件 | 试验值/kN | 预测值/kN | 预测值/试验值 |
| L1 | 85 | 91.89 | 1.081 |
| L2 | 115 | 112.96 | 0.982 |
| L3 | 232 | 226.89 | 0.978 |
| L4 | 230 | 226.89 | 0.986 |
4 结论
本研究研究了加固方式及有无预应力对采用TRC复合嵌入式预应力FRP筋加固RC梁抗弯性能的影响,并对其破坏形态、承载能力及裂缝分布进行了分析,最终构建了TRC复合嵌入式FRP筋加固RC梁的承载力计算公式并进行了验证,得出主要结论如下。
(1) 相较于对照梁和TRC加固梁,复合加固梁的开裂、屈服和极限荷载均提升明显。同时,预应力复合加固梁较无预应力复合加固梁开裂荷载提升明显。
(2) 复合加固梁的抗弯刚度明显高于未加固梁和TRC加固梁,钢筋屈服后预应力对复合加固梁抗弯刚度的影响较钢筋屈服前有所减小。
(3) 复合加固梁裂缝数量明显多于对照梁和TRC加固梁,但有无预应力对复合加固梁裂缝分布和裂缝数量影响较小。
(4) 纤维编织网和碳纤维筋可有效分担复合加固梁受拉钢筋中的应力。
(5) 采用截面分析方法构建了TRC复合嵌入式FRP筋加固RC梁的承载力计算公式,其极限承载能力与实测值的偏差均小于10%,这说明了该模型具有良好的适用性。
| [1] |
缑永涛, 尼颖升, 张永昌, 等. 劣化混凝土小箱梁混合加固抗弯承载力计算方法[J]. 公路交通科技, 2025, 42(5): 148-155. GOU Yongtao, NI Yingsheng, ZHANG Yongchang, et al. Calculation method for bending capacity of deteriorated concrete small box girder strengthened with hybrid reinforcement methods[J]. Journal of Highway and Transportation Research and Development, 2025, 42(5): 148-155. DOI:10.3969/j.issn.1002-0268.2025.05.016 |
| [2] |
任戈, 刘俊芳, 刘鸿飞, 等. 基于Eshelby夹杂理论高温冻土累积塑性应变修正模型[J]. 内蒙古工业大学学报(自然科学版), 2024, 43(4): 368-372. REN Ge, LIU Junfang, LIU Hongfei, et al. Modified model for cumulative plastic deformation in high-temperature permafrost based on Eshelby inclusions theory[J]. Journal of Inner Mongolia University of Technology (Natural Science Edition), 2024, 43(4): 368-372. |
| [3] |
黄建云, 尼颖升, 张永昌, 等. 开裂小箱梁承载力混合加固方法试验研究[J]. 公路交通科技, 2025, 42(4): 131-138. HUANG Jianyun, NI Yingsheng, ZHANG Yongchang, et al. Experimental study on bearing capacity hybrid reinforcement methods for cracked small box girder[J]. Journal of Highway and Transportation Research and Development, 2025, 42(4): 131-138. |
| [4] |
孙悦, 朱伟庆, 贾金青, 等. 型钢高强混凝土柱破坏模式与变形特征研究[J]. 内蒙古工业大学学报(自然科学版), 2024, 43(4): 351-359. SUN Yue, ZHU Weiqing, JIA Jinqing, et al. Failure modes and deformation characteristics of steel reinforced high-strength concrete columns[J]. Journal of Inner Mongolia University of Technology (Natural Science Edition), 2024, 43(4): 351-359. |
| [5] |
VERBRUGGEN S, TYSMANS T, WASTIELS J. TRC or CFRP strengthening for reinforced concrete beams: An experimental study of the cracking behaviour[J].
Engineering Structures, 2014, 77: 49-56.
DOI:10.1016/j.engstruct.2014.07.040 |
| [6] |
RAMPINI M C, ZANI G, COLOMBO M, et al. Mechanical behaviour of TRC composites: Experimental and analytical approaches[J/OL]. Applied Sciences, 2019, 9(7): 23. (2019-04-10) [2023-03-01]. https://doi.org/10.3390/app9071492.
|
| [7] |
尹世平, 王璐晨, 王聪聪, 等. 不同尺寸对TRC永久性模板叠合钢筋混凝土梁弯曲性能影响研究[J]. 建筑结构学报, 2021, 42(增1): 291-301. YIN Shiping, WANG Luchen, WANG Congcong, et al. Flexural performance of TRC permanent formwork reinforced concrete beams with different dimensions[J]. Journal of Building Structures, 2021, 42(S1): 291-301. |
| [8] |
CALABRESE A S, D'ANTINO T, COLOMBI P, et al. Low-and high-cycle fatigue behavior of FRCM composites[J/OL]. Materials, 2021, 14(18): 5412. (2021-09-18) [2023-03-01]. https://doi.org/10.3390/ma14185412.
|
| [9] |
郭嘉欢, 王伯昕, 张添奇, 等. 纤维编织网增强混凝土抗渗性能研究[J]. 东北大学学报(自然科学版), 2022, 43(9): 1354-1360. GUO Jiahuan, WANG Boxin, ZHANG Tianqi, et al. Study on impermeability of textile reinforced concrete[J]. Journal of Northeastern University (Natural Science), 2022, 43(9): 1354-1360. |
| [10] |
李雨珊, 尹世平, 刘运超. FRP筋与全珊瑚骨料海水混凝土界面粘结-滑移本构关系[J]. 复合材料学报, 2022, 39(8): 3950-3964. LI Yushan, YIN Shiping, LIU Yunchao. Bond-slip constitutive relation between FRP bars and coral aggregate seawater concrete[J]. Acta Materiae Compositae Sinica, 2022, 39(8): 3950-3964. |
| [11] |
ELJUFOUT T, TOUTANJI H. Fatigue behavior of prefatigued reinforced concrete beams rehabilitated with near surface mounted carbon fiber reinforced polymer reinforcement[J].
Structural Concrete, 2020, 21(2): 533-547.
DOI:10.1002/suco.201900131 |
| [12] |
HADDAD R H, ALMOMANI O A. Flexural performance and failure modes of NSM CFRP-strengthened concrete beams: A parametric study[J].
International Journal of Civil Engineering, 2019, 17: 935-948.
DOI:10.1007/s40999-018-0342-8 |
| [13] |
姚杰, 杨树桐, 张贤舜. FRP嵌入式加固带裂缝混凝土梁力学性能研究[J]. 混凝土, 2020(12): 35-37. YAO Jie, YANG Shutong, ZHANG Xianshun. Study on mechanical properties of FRP embedded reinforced concrete beams[J]. Concrete, 2020(12): 35-37. DOI:10.3969/j.issn.1002-3550.2020.12.008 |
| [14] |
KAMANI R, DOLATABADI M K, NASROLLAHZADEH K, et al. Bending load capacity of carbon fiber reinforced concrete beams as a function of fiber performance index (FPI)[J].
Journal of the Textile Institute, 2019, 110(4): 581-589.
DOI:10.1080/00405000.2018.1498625 |
| [15] |
尹世平, 盛杰, 徐世烺. 疲劳荷载下纤维编织网增强混凝土加固RC梁的弯曲性能[J]. 水利学报, 2014, 45(12): 1481-1486. YIN Shiping, SHENG Jie, XU Shilang. Experimental research of flexural performance of RC beams strengthened with TRC under fatigue load[J]. Journal of Hydraulic Engineering, 2014, 45(12): 1481-1486. |
| [16] |
徐世烺, 沈玲华, 王激扬, 等. 纤维编织网增强混凝土薄板的高温力学性能与微观界面粘结破坏分析[C]//中国力学学会, 《工程力学》杂志社. 第22届全国结构工程学术会议论文集第Ⅱ册. 北京: 人民交通出版社, 2013: 165-172. XU Shilang, SHEN Linghua, WANG Jiyang, et al. High-temperature mechanical property and microcosmic bonding failure of textile reinforced concrete slab [C] //The Chinese Society of Theoretical and Applied Mechanics, Journal of Engineering Mechanics. Proceedings of the 22nd National Conference on Structural Engineering(Vol Ⅱ). Beijing: China Communications Press; 2013: 165-172. |
| [17] |
YIN S P, HUA Y T, YU Y L. Flexural durability and chloride diffusion equation of TRC-strengthened beams under a chloride environment[J].
KSCE Journal of Civil Engineering, 2020, 24: 1868-1880.
DOI:10.1007/s12205-020-1640-7 |
| [18] |
尹世平, 余玉琳, 那明望. 氯盐侵蚀下TRC加固承载RC受弯梁抗裂性能[J]. 水利学报, 2018, 49(7): 886-891. YIN Shiping, YU Yulin, NA Mingwang. Crack resistance of loaded flexural TRC-strengthened beams under chloride erosion[J]. Journal of Hydraulic Engineering, 2018, 49(7): 886-891. |
| [19] |
尹世平, 余玉琳, 那明望. 氯盐侵蚀作用下TRC加固梁的受弯性能分析[J]. 华中科技大学学报(自然科学版), 2019, 47(2): 7-13. YIN Shiping, YU Yulin, NA Mingwang. Flexural performances analysis of TRC-strengthened beams under chloride corrosion[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(2): 7-13. |
| [20] |
盛杰. 海洋大气环境下TRC加固RC梁受弯时变性能[J]. 建筑结构学报, 2021, 42(增1): 284-290. SHEN Jie. Time-dependent behavior of RC beams strengthened with TRC in marine atmosphere environment[J]. Journal of Building Structures, 2021, 42(S1): 284-290. |
| [21] |
SHENG J, YU Z J, DOU G T, et al. Fatigue damage behaviors of TRC-strengthened RC beams[J].
Materials, 2022, 15(15): 5113.
DOI:10.3390/ma15155113 |
| [22] |
SHENG J, WANG L C, YIN S P. Study on the mechanical performance of TRC-strengthened RC beams under a salt freeze-thaw environment[J/OL]. Cold Regions Science and Technology, 2021, 192: 103384. https://doi.org/10.1016/j.coldregions.2021.103384.
|
| [23] |
尹世平. TRC基本力学性能及其增强钢筋混凝土梁受弯性能研究[D]. 大连: 大连理工大学, 2010. YIN Shiping. Study on basic mechanical properties of TRC and flexural behavior of reinforced concrete beams[D]. Dalian: Dalian University of Technology, 2010. |
 2025, Vol. 42
2025, Vol. 42



 ,
,