扩展功能
文章信息
- 李海, 陈嘉祺, 谭明, 汤铭锋.
- LI Hai, CHEN Jiaqi, TAN Ming, TANG Mingfeng
- 高速公路超高渐变段汇水路径及积水分布特性
- Catchment path and water log distribution at expressway superelevation transition sections
- 公路交通科技, 2025, 42(8): 90-102
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(8): 90-102
- 10.3969/j.issn.1002-0268.2025.08.010
-
文章历史
- 收稿日期: 2025-03-31
2. 中南大学 土木工程学院, 湖南 长沙 410075;
3. 广西交投科技有限公司, 广西 南宁 530028;
4. 广西高速公路养护工程技术研究中心, 广西 南宁 530028;
5. 广西交投科技有限公司 广西交通运输行业道路智慧养护重点实验室, 广西 南宁 530028
2. School of Civil Engineering, Central South University, Changsha, Hunan 410075, China;
3. Guangxi Jiaotou Science and Technology Co., Ltd., Nanning, Guangxi 530028, China;
4. Guangxi Expressway Maintenance Engineering Technology Research Centre, Nanning, Guangxi 530028, China;
5. Guangxi Transportation Industry Key Laboratory of Road Smart Maintenance, Guangxi Communications Investment Science and Technology Co., Ltd., Nanning, Guangxi 530028, China
路面积水是影响公路交通安全的重要问题之一。在设计中通常会合理设置横纵坡并布设相应的排水设施以解决积水问题。由于独特的横纵坡变化特点,超高渐变段汇水路径和水膜厚度的分布更加复杂,易产生积水[1-3]。积水的形成不仅增加了车辆行驶阻力,还会显著降低轮胎与路面之间的附着力[4],增加滑水事故的风险。在超高渐变段设计过程中,路面积水的汇集路径受到道路横坡、纵坡、路幅宽度等几何参数的共同影响[5-6]。深入分析路面几何参数对汇水路径及积水分布特性的影响,对改善超高渐变段的积水情况具有重要意义。
针对超高渐变段汇水路径与几何设计之间的相互作用机制已有一定的研究基础。管朝鹏[7]运用Fluent软件对路表水的形成、流动及水膜厚度的汇聚进行模拟,对超高渐变段路面的积水情况进行了深入分析。张卓[8]基于动力学原理和有限差分法,建立了“S”形曲线超高渐变段的水流路径长度计算模型,探讨了纵坡与水流路径长度的关系。Jeong[9]开发了基于扩散波理论的二维有限体积模型,用于模拟在超高渐变段上的雨水汇流过程,研究了超高渐变段几何设计对汇水路径的影响。耿艳芬[10]基于二维浅水方程,研究了降雨条件和道路几何特性对路面径流及行车安全的影响。张燕飞[11]利用纬地交通工程与安全设施CAD软件,结合计算流体动力学仿真方法,建立了超高渐变段水膜厚度与道路纵坡、超高渐变率、降雨强度和水流路径长度之间的回归模型。现有研究虽然揭示了在特定阈值范围内几何参数对汇水路径的影响规律,但在真实道路环境中,几何参数的整体作用机制尚未得到充分解析,难以准确反映最大汇水路径的变化特征。
对超高渐变段路面积水的分析主要采用试验标定、理论推演与数值仿真等方法进行研究。罗京[12]通过室内大型降雨模拟试验标定了路面水膜厚度计算公式,提出了一种定量化的水膜厚度检验评价方法。Wang[13]构建了无明显汇水阶段、自由排水阶段和受阻排水阶段的水膜厚度理论模型,通过理论和数值方法预测了积水分布及水膜厚度。张驰[14]引入流体力学中的圣维南方程组和曼宁公式,结合有限元分析方法,构建了超高渐变段积水深度分布模型。孙毅凯[15]利用Fluent软件建立了水流仿真模型,采用RNGk-ε湍流模型、离散相模型和欧拉壁膜模型,耦合实现降雨和水流路径的计算。现有研究多集中于以水膜厚度、汇水路径等参数作为超高渐变段研究指标,但对水膜厚度的分布情况与汇水路径之间的交互关系缺乏系统性解析。
为深入探究超高渐变段汇水路径与水膜厚度分布的交互关系,揭示道路几何参数对二者的影响规律。本研究基于最大合成坡度原理创建超高渐变段最大汇水路径长度计算方法,基于离散相模型与欧拉壁膜模型进行路面降雨分析,系统研究了不同几何参数对超高渐变段汇水路径及积水分布特性的影响,为超高渐变段路面的排水设计与交通安全提供依据。
1 模型参数确定本研究主要针对高速公路超高渐变段进行建模研究,系统分析不同几何参数下的最大汇水路径变化规律及积水分布特性。考虑到线路的对称性,选取高速公路的右侧路幅进行分析。模型中路面宽度参照双向四车道、双向六车道及双向八车道的标准路幅构成,分别为11.25,15.0,18.75 m。依据《公路路线设计规范》(JTG D20—2017)中纵坡与超高渐变率的技术要求,超高渐变段模型的关键几何参数取值如表 1所示。
| 路幅宽度/m | 路面纵坡/% | 超高渐变率 | 路面整体长度/m |
| 11.25,15.0,18.75 | 0.3~3.0 | 1/330~1/200 | 90.0~247.5 |
2 最大汇水路径分析 2.1 最大汇水路径计算方法
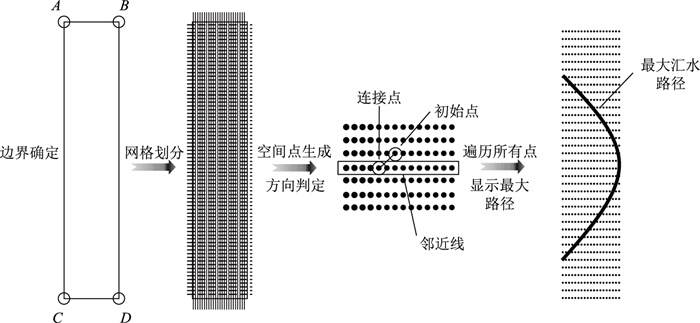
相关研究表明,在重力作用下,水流主要沿道路合成坡度方向汇集,直至排出路表[10, 16]。在特定道路线形条件下, 行车道范围内水流汇集形成点至其流出点的最大几何长度称为最大汇水路径长度[17]。本研究基于以上原理进行特定几何参数下的超高渐变段最大汇水路径计算,计算流程如图 1所示。基于Matlab编程计算最大汇水路径,整体过程如下。
|
| 图 1 最大汇水路径计算流程示意图 Fig. 1 Schematic diagram of maximum catchment path calculation process |
| |
(1) 依据超高渐变段的纵坡、超高渐变率及路幅宽度,确定路段长度与左右路幅边界起始点和终止点坐标,即图 1中A,B,C,D这4个点,确保路径计算能够覆盖整个超高渐变段区域。
(2) 划分网格如图 1所示。所有网格点生成完整的离散坐标点集,组成路面整体的三维空间点模型,准确反映超高渐变段的几何形态及其变化特征。
(3) 从三维路面空间点模型中选取路径初始点,根据该点的纵坡判断路线的下坡方向。计算初始点与下坡方向邻近线上各点连线的坡度,选取坡度最大的线路作为初始点的合成坡度方向。将初始点沿合成坡度方向与下一个点进行连接以实现汇水路径的延伸。
(4) 以连接点作为新的初始点,继续进行汇水路经计算。每次水流延伸时计算2点之间的距离并更新路径长度,当汇水路经延伸至道路边界时,可视为该条汇水路径已排出路面外,停止计算。
(5) 通过遍历所有点,计算每个点作为初始点的汇水路径,选择最长的路径作为该几何参数下的超高渐变段最大汇水路径,输出该路径所经过的所有点的坐标。
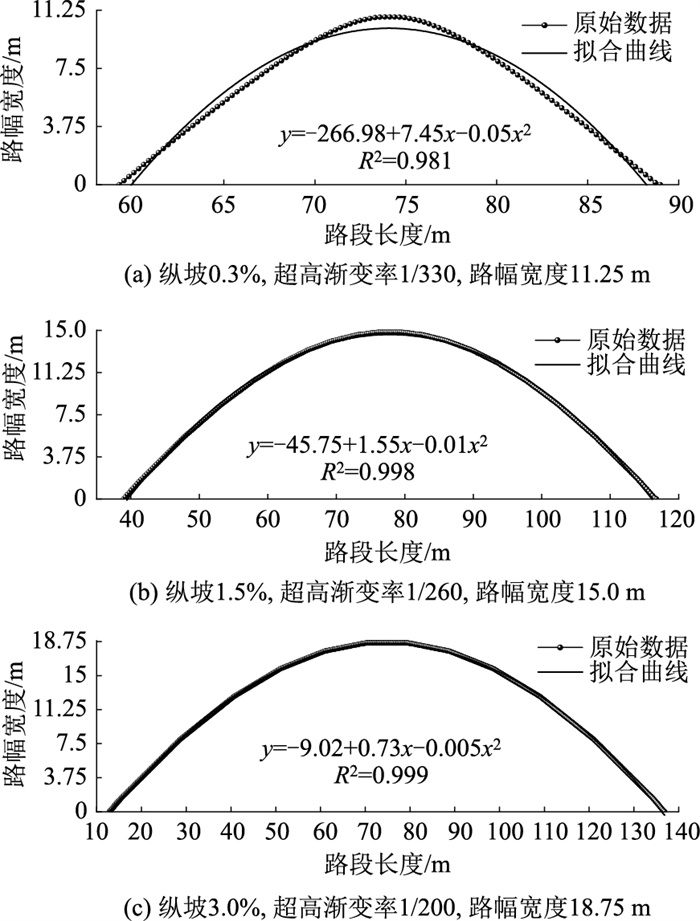
2.2 最大汇水路径形态及方向分析为研究最大汇水路径的具体形态,基于路径点坐标数据对最大汇水路径进行曲线回归分析,如图 2所示。由于工况较多,选取参数下限组合(纵坡0.3%,超高渐变率1/330,路幅宽度11.25 m)、中间参数组合(纵坡1.5%,超高渐变率1/260,路幅宽度15 m)及参数上限组合(纵坡3.0%,超高渐变率1/200,路幅宽度18.75 m)进行分析。分析结果表明,最大汇水路径曲线高度符合抛物线分布特征,上述3种组合的R2分别为0.981,0.998,0.999,可以认为超高渐变段最大汇水路径的形状呈抛物线形。超高渐变段在超高渐进变化的过程中会出现横坡为0的截面,该截面与最大汇水路径的中线相重合,截面与最大汇水路径的交点处为抛物线顶点。
|
| 图 2 最大汇水路径曲线回归分析 Fig. 2 Regression analysis on maximum catchment path curves |
| |
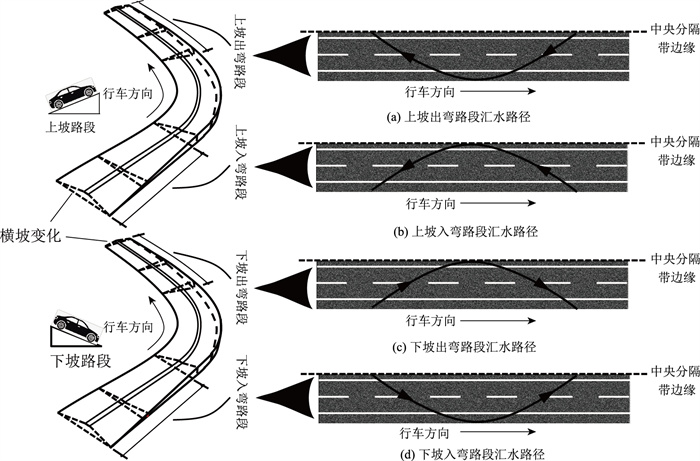
最大汇水路径方向如图 3所示,路面内箭头代表水流汇聚方向,根据起始点位置的不同将方向分为2种情况。情况1为水流由中央分隔带流向硬路肩边缘,再由硬路肩边缘返回至中央分隔带。该情况主要出现在上坡出弯路段或下坡入弯路段,如图 3(a)和图 3(d)所示。情况2为水流由硬路肩边缘流向中央分隔带,再由中央分隔带返回至硬路肩边缘。该情况主要出现在上坡入弯路段或下坡出弯路段,如图 3(b)和图 3(c)所示。
|
| 图 3 最大汇水路径方向 Fig. 3 Maximum catchment path directions |
| |
2.3 最大汇水路径长度分析 2.3.1 纵坡对最大汇水路径的影响分析
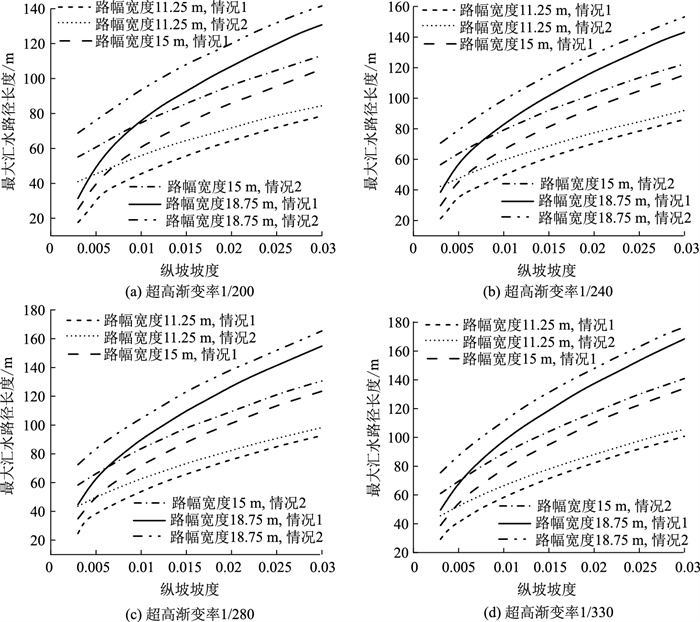
基于2.1节最大汇水路径计算结果,情况1和情况2的最大汇水路径长度与路面纵坡坡度的关系如图 4所示。图 4(a)表示超高渐变率1/200时的情况,其他超高渐变率下的关系规律基本一致。当超高渐变率一定时,随着路面纵坡坡度的增大,最大汇水路径长度逐渐增加。这主要是由于较大的纵坡促使水流沿路段纵向持续、稳定地扩展,进而延长了最大汇水路径长度。此外,在超高渐变率、纵坡坡度、路幅宽度均固定的情况下,情况2的最大汇水路径长度始终大于情况1。当纵坡坡度较小时,情况1的最大汇水路径长度增长速率明显高于情况2,在纵坡小于超高渐变率时,这种现象尤为明显。
|
| 图 4 最大汇水路径长度与纵坡关系 Fig. 4 Relation of maximum catchment path length and longitudinal gradient |
| |
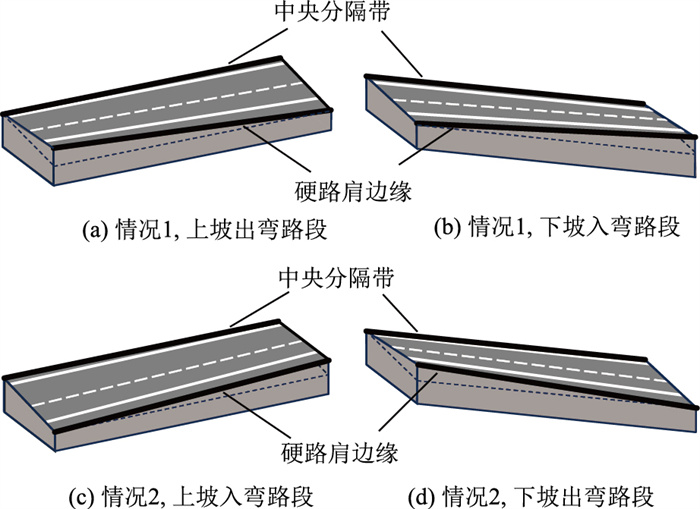
为进一步分析2种情况汇水路径变化的原因,绘制超高渐变前后情况1与情况2的路面示意图,如图 5所示。图中虚线表示超高渐变前的硬路肩边缘。当路段属于情况1时,如图 5(a)和图 5(b)所示,超高渐变后硬路肩边缘处沿路线方向的纵向坡度小于中央分隔带沿路线方向的纵向坡度。硬路肩边缘区域相对更加平缓,水流在该区域的纵向流速相对减缓,限制水流沿纵向的延伸,进而缩短了最大汇水路径的长度。而当路段属于情况2时,如图 5(c)和图 5(d)所示,超高渐变后硬路肩边缘处沿路线方向的纵向坡度大于中央分隔带沿路线方向的纵向坡度。硬路肩边缘区域相对更加陡峭,水流在该区域的纵向流速相对加快,增强了水流沿纵向的延伸能力。因此情况2的最大汇水路径长度总是大于相同条件下情况1的最大汇水路径长度。
|
| 图 5 超高渐变后的路面示意图 Fig. 5 Schematic diagram of pavement after superelevation transition |
| |
取情况1中路幅宽度为11.25 m,超高渐变率为1/200时的最大汇水路径计算结果进一步分析,如图 6所示。当纵坡小于超高渐变率时,最大汇水路径的顶点并未到达硬路肩边缘线附近,而是在行车道中部,如图 6(a)和图 6(b)所示。随着纵坡的增大,顶点逐渐向硬路肩边缘线移动,直至纵坡与超高渐变率相等时,中点到达硬路肩边缘线,如图 6(c)所示。当纵坡小于超高渐变率时,由于纵坡过小且超高渐变后硬路肩边缘较为平缓,最大汇水路径的纵向与横向扩展同时受到抑制。随着纵坡增大,最大汇水路径的顶点逐渐由行车道中部向硬路肩边缘移动,路径在横向和纵向同时扩展,此时路径长度增长速率较快。当纵坡与超高渐变率相等后,路径顶点到达硬路肩边缘,路径只能在纵向继续扩展,增长速率随之放缓。

|
| 图 6 最大汇水路径计算结果 Fig. 6 Calculation result for maximum catchment path |
| |
2.3.2 超高渐变率对最大汇水路径的影响分析
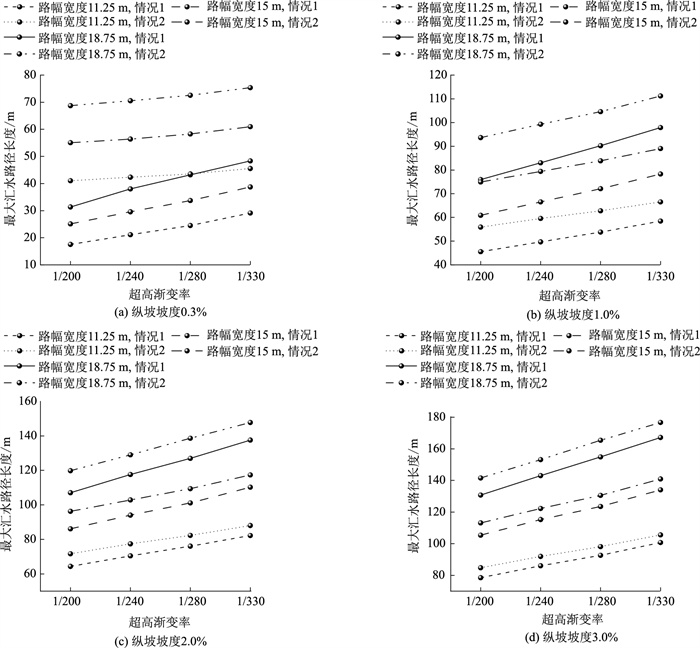
情况1和情况2的最大汇水路径长度与超高渐变率的关系如图 7所示。在纵坡坡度与路幅宽度一定时,随着超高渐变率的减小,路段的最大汇水路径长度逐渐增加。这是由于较小的超高渐变率(即横坡变化更加平缓)对水流横向汇集的引导能力较弱,导致水流倾向于沿纵坡方向进行汇聚。而较大的超高渐变率由于横坡的坡度较陡,对水流的横向引导能力更强,水流更容易快速排出,导致汇水路径较短。
|
| 图 7 最大汇水路径与超高渐变率关系 Fig. 7 Relation of maximum catchment path and superelevation runoff |
| |
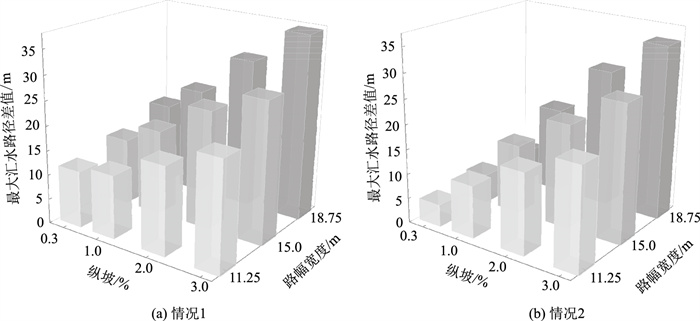
基于图 7结果,计算超高渐变率为1/330与1/200时的最大汇水路径长度差值,如图 8所示。由图可知,无论对于哪种路幅宽度,当路段纵坡坡度较小时最大汇水路径差值较小,即最大汇水路径长度随超高渐变率的变化较小。随着纵坡坡度的增大,最大汇水路径长度随超高渐变率的变化显著增强。这是因为当纵坡较小时,水流汇集主要受横坡影响,而最大汇水路径长度增加主要依靠纵向的延伸。此时即使调整超高渐变率,由于纵坡的影响较弱,水流沿纵向的延伸有限,水流路径的变化仍然不会显著。当纵坡增大时,水流的纵向流动增强,此时如果超高渐变率小(横坡变化缓慢),水流更倾向于沿纵向持续流动,导致路径长度增加,进而导致不同超高渐变率下的路径长度差值变大。
|
| 图 8 最大汇水路径差值变化 Fig. 8 Variation of maximum catchment path differentials |
| |
2.3.3 路幅宽度对最大汇水路径的影响分析
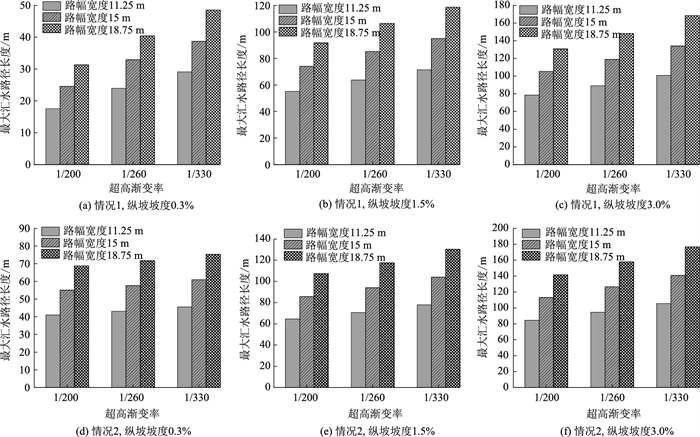
基于2.1节最大汇水路径计算结果,情况1和情况2的最大汇水路径长度与路幅宽度的关系如图 9所示。由图可见,在纵坡与超高渐变率固定的条件下,最大汇水路径长度与路幅宽度呈正相关。
|
| 图 9 最大汇水路径与路幅宽度关系 Fig. 9 Relation of maximum catchment path and road width |
| |
经计算,路幅宽度为15 m时的最大汇水路径长度约为11.25 m时的1.33倍,路幅宽度为18.75 m时约为11.25 m时的1.67倍,与路幅宽度的几何比例一致。为验证这一结论,分析最大汇水路径估计值与计算值的关系,如图 10所示。图中横坐标表示路幅宽度为11.25 m时各工况下的最大汇水路径数据乘以1.33得到的估计值,纵坐标表示路幅宽度为15 m时各工况下的最大汇水路径计算值。灰色直线代表函数y=x,数据点越接近该线,表明计算值与估计值越吻合。可以发现,无论是情况1还是情况2,路幅宽度为15 m时各工况下的最大汇水路径均接近路幅宽度为11.25 m时最大汇水路径的1.33倍。当路幅宽度为18.75 m时各工况下的最大汇水路径均接近路幅宽度为11.25 m时最大汇水路径的1.67倍。

|
| 图 10 最大汇水路径估计值与计算值关系 Fig. 10 Estimated values v.s. calculated values of maximum catchment path |
| |
3 积水分布特性分析 3.1 路面降雨模型建立
降雨后路表形成积水是一个复杂的两相过程,涉及雨滴的形成与下落、雨滴与路面接触形成水膜、以及水膜的汇聚与流动等多个环节。雨水与路面的相互作用不仅受到降雨强度、路面结构等因素的影响,还受到重力、水的表面张力及其他参数的作用,精确模拟这一过程对于提高超高渐变段排水设计的可靠性至关重要。本研究采用ANSYS Fluent 2022中流体模块针对超高渐变段路面积水问题进行数值模拟与计算。采用离散相模型与欧拉壁膜模型进行路面积水分析。离散相模型将离散相与连续相进行耦合,能够详细描述雨滴在空气中的运动轨迹,包括雨滴的下落、碰撞,通过模拟雨滴的轨迹和与路面的相互作用,分析不同降水强度、路面构造等因素对积水现象的影响。欧拉壁膜模型被广泛应用于模拟三维壁面薄液膜的形成与流动,能够准确分析降雨后路面水膜的形成与汇聚情况。
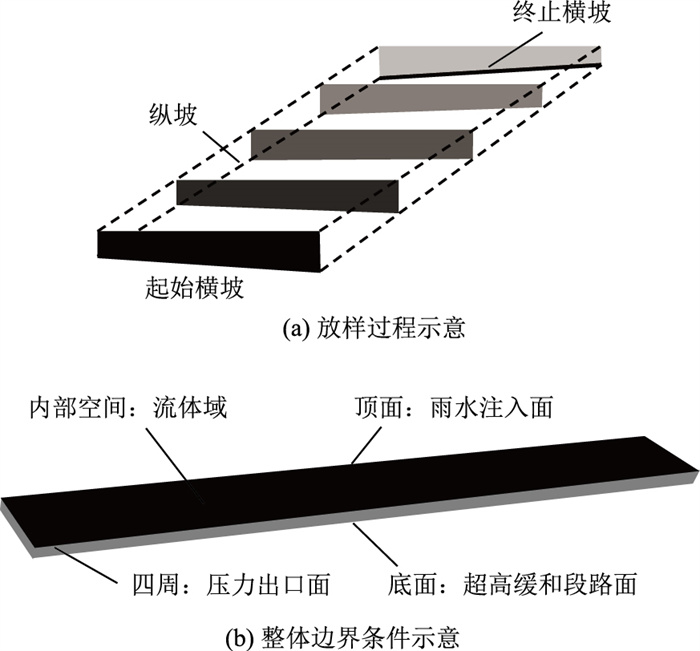
路面降雨模型示意图如图 11所示, 模型实体采用放样方式进行建立,包括顶部规则降雨平面、内部流体域、底部不规则超高渐变段路面,如图 11(a)所示。网格划分从规则的上表面开始,使用边长0.25 m的正方体网格单元。随着网格向下划分至不规则的超高渐变面时,通过自适应调整层高,确保网格贴合不规则底面。
|
| 图 11 路面降雨模型示意图 Fig. 11 Schematic diagrams of surface rainfall model |
| |
整体边界条件如图 11(b)所示。模型实体顶面设置为雨水注入面,在该面添加注射源。降雨强度设置为2 mm/min,属于特大暴雨等级,以模拟短时强降雨条件下超高渐变段的积水动态变化特征。在该降雨条件下,驾驶员视距尚在200 m左右[18],视觉感知并未完全丧失,通常不会立即采取制动或减速等主动避险行为,仍保持较高车速行驶,从而显著增加发生水滑等交通事故的风险。雨滴的直径、持续时间和总流量等参数如表 2所示。
| 入射速度/(m·s―1) | 雨滴直径/mm | 持续时间/s | 总流量/(kg·s―1) |
| 6 | 2.75 | 300 | 33.75~154.69 |
模型实体内部空间为流体域,雨水可以存在于该空间中并进行运动。模型实体的四周设置为压力出口面,采用分散式排水方式,一旦路面表面的水流出路幅范围,便不再考虑其对表面水流的影响。模型实体底面为超高渐变段路面,设置为壁面,雨水可以在该面进行汇聚与流动。依据《公路路基路面现场测试规程》(JTG 3450—2019) 对路面构造深度及摩擦系数的规定,设置壁面的路面构造深度为1 mm,摩擦系数为0.5。在仿真过程中,雨水从注入面进入模型,在流体域中模拟降水过程中的雨滴下落,降落在超高渐变段路面后逐渐积累形成水膜,在重力、水的表面张力作用下进行汇聚与流动,最终通过压力出口面进行排出,随着时间推移,路表水膜厚度会趋近于稳定状态。
3.2 积水分布特性影响因素分析 3.2.1 纵坡对积水分布特性的影响分析基于模型的计算结果,确定固定超高渐变率为1/200,路幅宽度11.25 m,情况1与情况2沿最大汇水路径的积水分布随纵坡的变化如图 12所示。图中横坐标为归一化汇水路径长度,数值为计算位置与整条路经的相对比例,0代表路径起点,0.5代表路径顶点,1.0代表路径终点。分析可得,随着纵坡增加,情况1沿最大汇水路径的积水变化趋势主要呈现为3种曲线形式。形式1,如图 12(a)中纵坡0.3%时所示。路面水膜厚度随着路径的延伸呈现单峰值状态,最大水膜厚度处位于最大汇水路径顶点附近。形式2,如图 12(a)中纵坡1.0%时所示。路面水膜厚度随着路径的延伸呈现双峰值状态,第1峰值出现在路径进度的25%附近,第2峰值出现在路径进度的80%附近。形式3,如图 12(a)中纵坡2.0%时所示。路面水膜厚度随着路径的延伸呈现持续增长状态,水膜厚度峰值位于最大汇水路径末尾段。其中,形式1的最大水膜厚度为三者中的最大值,相较形式2和形式3分别高出20.5%和8.6%。情况2最大汇水路径上的水膜厚度变化趋势只有双峰值状态和持续增长状态,而未出现单峰值状态。后续主要针对情况1分析产生上述3种形式的原因。

|
| 图 12 积水分布情况与纵坡关系 Fig. 12 Relation of water log distribution and longitudinal gradient |
| |
为直观分析3种形式的积水变化趋势,超高渐变率为1/200,纵坡设置为0.3%,1.0%,2.0%时情况1的积水分布示意如图 13所示。依据图中积水变化趋势,可以分析不同几何参数的超高渐变路段最大水膜厚度出现的位置。图中水膜厚度为红色的区域代表厚度相对较大,更易影响交通安全,在超高渐变段路面排水设施布置时应重点关注。针对积水分布的3种曲线形式分析如下。

|
| 图 13 路面积水的3种分布形式 Fig. 13 Three patterns of water log distribution |
| |
(1) 如图 13(a)所示,当路面纵坡小于超高渐变率时,最大汇水路径的顶点位于行车道中部。该处附近的横坡与纵坡较小,横坡不足以将水流分散至道路两侧,纵坡的排泄驱动力也不足以有效推动水流向下游方向排泄。水流持续积聚,导致路面水膜厚度呈现单一峰值状态,峰值位置集中在最大汇水路径的顶点附近。
(2) 如图 13(b)所示,随着纵坡增大,最大汇水路径的顶点逐渐到达道路边缘。此时水流已经能在横纵坡共同作用下沿着最大汇水路径汇聚,整体的水膜厚度呈现上升趋势。但靠近道路边缘处的部分,水的重力横向扩散排出道路的能力强于横纵坡的引导作用,因此道路边缘处的水膜厚度出现一定程度的降低,导致整条路径水膜厚度分布出现双峰值的状态。
(3) 如图 13(c)所示,当纵坡足够大时,路面的排水能力显著增强,此时最大汇水路径较长。水流在横坡与纵坡的共同作用下沿最大汇水路径持续汇聚,水膜厚度持续增长,最大水膜厚度出现在最大汇水路径的末尾段。
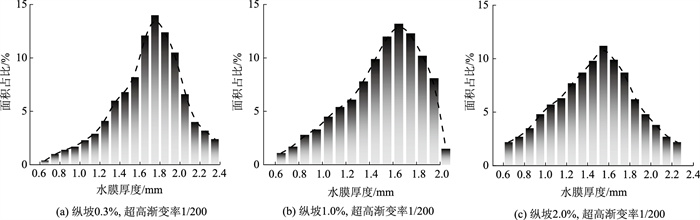
基于模型计算得到的水膜厚度分布结果,对固定超高渐变率1/200,纵坡坡度分别为0.3%,1.0%,2.0%时整个路面不同水膜厚度区间的面积占比进行统计分析,如图 14所示。当路面纵坡较小时(见图 14(a)),由于道路纵向排水能力有限,路面整体的水膜厚度偏大。水膜厚度超过1.6 mm的区域占比达到65.2%,水膜厚度超过2 mm的区间主要集中分布于超高渐变段中部横坡较缓的区域。随着纵坡增大,道路排水能力增强,整体水膜厚度呈下降趋势,水膜厚度低于1.6 mm的区域面积占比不断上升。当路面纵坡为2.0%时(见图 14(c)),水膜厚度低于1.6 mm的区域占比达到62.6%,存在少部分水膜厚度超过2 mm的区域,主要集中于最大汇水路径的末尾段。
|
| 图 14 路面水膜厚度区间的面积占比 Fig. 14 Area ratios of various intervals with different pavement water film thicknesses |
| |
3.2.2 超高渐变率对积水分布特性的影响分析
固定路幅宽度为11.25 m,纵坡坡度分别为0.3%,1.0%,2.0%,沿最大汇水路径上的积水分布情况与超高渐变率的关系如图 15所示。当纵坡为0.3%时,随着超高渐变率的减小,积水的分布逐渐由单峰值状态向双峰值状态过渡。这是由于随着超高渐变率减小,最大汇水路径的顶点由行车道中部逐渐向道路边缘移动,从而改变了水流的排泄路径。当纵坡坡度为1.0%和2.0%时,最大汇水路径上的水膜厚度整体随着超高渐变率的降低而增大,但其沿最大汇水路径的分布趋势基本保持不变。具体而言,当纵坡坡度为1.0%和2.0%时,超高渐变率为1/330的路面最大水膜厚度值相较于1/200分别提高了11.5%和18.0%。

|
| 图 15 积水分布情况与超高渐变率关系 Fig. 15 Relation of water log distribution and superelevation runoff |
| |
综合分析可知,当纵坡小于超高渐变率时,超高渐变率对水膜厚度的影响主要体现在沿最大汇水路径的分布趋势。当纵坡大于超高渐变率后,超高渐变率对水膜厚度的影响主要体现在厚度的绝对值上,随着超高渐变率的减小,水膜厚度数值持续增长。
3.2.3 路幅宽度对积水分布特性的影响分析固定超高渐变率为1/200,纵坡坡度分别为0.3%,1.0%,2.0%时,最大汇水路径上的积水分布情况与路幅宽度的关系如图 16所示。分析结果表明,在超高渐变率和纵坡一致的条件下,不同路幅宽度的水膜厚度沿最大汇水路径的分布趋势基本保持一致,路幅宽度主要影响水膜厚度的绝对值。随着路幅宽度的增大,水膜厚度整体呈现出增加的趋势。具体而言,在3种纵坡条件下,路幅宽度为18.75 m的路面最大水膜厚度值相较于11.25 m分别提高了26.6%,20.6%,18.6%。路幅宽度的增大显著加剧了水膜的堆积效应, 由于路幅宽度的增加导致汇水路径变长,宽幅道路的水流更难快速排出,从而形成更厚的水膜。

|
| 图 16 积水分布情况与路幅宽度关系 Fig. 16 Relation of water log distribution and road width |
| |
3.3 工程应用
综合3.2节分析结果,不同类型的积水分布形式对应不同的积水集中区域和排水风险点,针对性地提出排水措施对于提升超高渐变段的排水效率和道路通行安全具有重要意义。当积水分布呈单峰值状态时,水膜厚度峰值通常位于行车道中部。该区域由于横纵坡引导能力有限,水流易于聚集且排出缓慢,积水深度相对较大。在实际道路设计与养护中,建议铣刨原有面层并重铺结构透水性较强的排水沥青混合料,以增强路面的渗排能力,从根源上减少水膜积聚。当积水分布呈双峰值状态时,积水主要集中于最大汇水路径顶点的两侧。针对这种积水模式,建议在路径顶点两侧布设横向刻槽或浅沟槽结构。通过增强横向排水路径的引导能力,加速水膜向两侧排出,减少两侧峰值区域的水膜厚度。当积水分布呈持续增长状态时,积水往往沿最大汇水路径逐渐累积,并最终聚集于路径的末端区域,形成稳定性差、易诱发滑水的高风险积水点。针对该类型,应重点强化末端区域的排水能力。建议在最大汇水路径末端设置集中式排水口或横向集水井,并结合排水井设置相应的盲沟或透水基层引流结构,确保末端积水能够快速排除,减少在短时强降雨条件下的超限积水风险。
4 结论基于本研究提出的最大汇水路径长度计算方法及路面降雨模型,对不同几何参数下超高渐变段的最大汇水路径长度及积水分布情况进行了详细分析,揭示了纵坡、超高渐变率及路幅宽度3种几何参数的影响规律,主要结论如下。
(1) 超高渐变段的最大汇水路径整体呈抛物线形,抛物线顶点位于横坡为0的截面。路径分布可归纳为2种情况:情况1为水流由中央分隔带流向硬路肩边缘,再从硬路肩边缘返回至中央分隔带,主要出现在上坡出弯路段或下坡入弯路段。情况2为水流由硬路肩边缘流向中央分隔带,再从中央分隔带返回至硬路肩边缘,主要出现在上坡入弯路段或下坡出弯路段。设计时应结合坡度与行车方向识别路径类型,优化排水坡度与设施布设策略。
(2) 最大汇水路径长度随纵坡的增大逐渐增加,情况1当纵坡小于超高渐变率时,路径长度随纵坡的增长速率较快,其他情况下路径长度增长速率趋于平稳。最大汇水路径长度随超高渐变率的减小逐渐增长,在较大纵坡条件下超高渐变率的影响更为显著。在同一纵坡与超高渐变率条件下,15 m和18.75 m路幅宽度下的路径长度分别约为11.25 m路幅下的1.33倍与1.67倍,与其宽度几何比例高度一致。
(3) 在情况1中,沿最大汇水路径的积水分布形式随纵坡的增大依次呈现为单峰型、双峰型和持续增长型;而在情况2中,仅表现为双峰型和持续增长型。其中,单峰型分布对应的水膜厚度相对较大,水膜厚度超过1.6 mm的区域面积占比超过60%,对行车安全影响显著。随着纵坡的增加,超高渐变率对水膜厚度的作用机制发生转变:从主要影响其沿路径的分布趋势,逐渐过渡为影响水膜厚度的绝对值。当纵坡为1.0%和2.0%时,当超高渐变率由1/200减小至1/330,最大水膜厚度分别增加11.5%和18.0%。此外,路幅宽度的增加显著加剧了水膜的堆积效应。在纵坡坡度为0.3%,1.0%,2.0%这3种条件下,路幅宽度由11.25 m增至18.75 m时,最大水膜厚度分别提升了26.6%,20.6%,18.6%。尽管厚度有所增加,但其沿最大汇水路径的分布趋势基本保持一致。
(4) 在不同几何参数条件下,超高渐变段汇水路径上最大水膜厚度的位置存在差异。为提升排水设计的精准性与有效性,工程实践中应重点关注水膜厚度显著区域的布设与处理。此外,道路的构造深度及降雨强度等因素会对路面的整体积水情况造成一定的影响,本研究固定了上述参数,未对其进行深入探讨,未来研究可通过调整这些参数进行仿真模拟,进一步揭示超高渐变段最大汇水路径及其积水分布规律。
| [1] |
贾兴利, 陈星澎, 黄平明, 等. 高速公路超高过渡段几何线形对小型客车滑水速度的影响[J]. 交通运输工程学报, 2022, 22(4): 140-147. JIA Xingli, CHEN Xingpeng, HUANG Pingming, et al. Influence of geometric alignment of expressway superelevation transition section on hydroplaning speed of minibus[J]. Journal of Traffic and Transportation Engineering, 2022, 22(4): 140-147. |
| [2] |
张驰, 向宇杰, 林宣财, 等. 考虑坡面排水的公路超高缓和段坡度组合设计[J]. 铁道科学与工程学报, 2022, 19(8): 2278-2286. ZHANG Chi, XIANG Yujie, DU Xuancai, et al. Slope combination design of highway superelevation transition section considering slope drainage[J]. Journal of Railway Science and Engineering, 2022, 19(8): 2278-2286. |
| [3] |
王贵山, 胡昌亮, 白浩晨, 等. 高速公路圆曲线超高及过渡段设计研究[J]. 公路交通科技, 2021, 38(12): 47-55. WANG Guishan, HU Changliang, BAI Haochen, et al. Study on design of expressway circular curve superelevation and transition section[J]. Journal of Highway and Transportation Research and Development, 2021, 38(12): 47-55. DOI:10.3969/j.issn.1002-0268.2021.12.006 |
| [4] |
高雪池, 毕玉峰, 季晓歌, 等. 考虑路面-轮胎-径流耦合作用的高速公路超宽路面排水设计[J]. 公路交通科技, 2024, 41(11): 94-103. GAO Xuechi, BI Yufeng, JI Xiaoge, et al. Super-wide expressway pavement drainage design considering road-tire-runoff coupling effect[J]. Journal of Highway and Transportation Research and Development, 2024, 41(11): 94-103. DOI:10.3969/j.issn.1002-0268.2024.11.011 |
| [5] |
程正刚. 纵坡和超高渐变率对超高过渡段水膜影响分析[J]. 城市道桥与防洪, 2024(11): 87-90, 22. CHENG Zhenggang. Analysis on influence of longitudinal slope and ultra-high gradient on water film in ultra-high transition section[J]. Urban Roads Bridges & Flood Control, 2024(11): 87-90, 22. |
| [6] |
屈强, 李星, 吴明先, 等. 基于行车稳定性的高速公路超高过渡方式对比研究[J]. 公路交通科技, 2021, 38(9): 15-24. QU Qiang, LI Xing, WU Mingxian, et al. Comparative study on expressway super-elevation transition modes based on driving stability[J]. Journal of Highway and Transportation Research and Development, 2021, 38(9): 15-24. DOI:10.3969/j.issn.1002-0268.2021.09.003 |
| [7] |
管朝鹏. 基于DPM及EWF模型的积水分布研究[D]. 重庆: 重庆交通大学, 2015. GUAN Zhaopeng. Study on the distribution of ponding water based on DPM and EWF[D]. Chongqing: Chongqing Jiaotong University, 2015. |
| [8] |
张卓, 高建平. 考虑水流路径长度的S型曲线超高段纵坡研究[J]. 重庆交通大学学报(自然科学版), 2013, 32(4): 594-596, 691. ZHANG Zhuo, GAO Jianping. Longitudinal slope at super-elevation sections of S curve considering flow path length[J]. Journal of Chongqing Jiaotong University (Natural Science), 2013, 32(4): 594-596, 691. |
| [9] |
JEONG J, CHARBENEAU R J. Diffusion wave model for simulating storm-water runoff on highway pavement surfaces at superelevation transition[J].
Journal of Hydraulic Engineering, 2010, 136(10): 819-828.
|
| [10] |
耿艳芬, 陈先华, 陈悦, 等. 基于二维浅水方程的直线段沥青路面径流特性[J]. 交通运输工程学报, 2019, 19(1): 9-16. GENG Yanfen, CHEN Xianhua, CHEN Yue, et al. Runoff characteristics for straightline segment asphalt pavement based on two-dimensional shallow water equations[J]. Journal of Traffic and Transportation Engineering, 2019, 19(1): 9-16. |
| [11] |
张燕飞. 降雨条件下多车道高速公路超高过渡段交通安全保障技术研究[D]. 西安: 长安大学, 2020. ZHANG Yanfei. Study on traffic safety assurance technology for superelevation transition section of multi-lane expressway under rainy condition[D]. Xi'an: Chang'an University, 2020. |
| [12] |
罗京, 刘建蓓, 戈普塔, 等. 路面水膜厚度检验评价方法[J]. 交通信息与安全, 2016, 34(6): 54-59, 82. LUO Jing, LIU Jianbei, GUPTA Pramod Kumar, et al. An inspection and evaluation method of thickness of water film on road surface[J]. Journal of Transport Information and Safety, 2016, 34(6): 54-59, 82. |
| [13] |
WANG K N, LI P L, AI Q, et al. Study on water distribution characteristics of surface gathered water and water film thickness model[J].
Alexandria Engineering Journal, 2022, 61(4): 3293-3302.
|
| [14] |
张驰, 周郁茗, 张昆仑, 等. 暴雨条件下高速公路超高缓和段积水深度分布模型构建[J]. 重庆交通大学学报(自然科学版), 2023, 42(6): 32-39. ZHANG Chi, ZHOU Yuming, ZHANG Kunlun, et al. The accumulated water depth distribution model of superelevation runoff of highway under rainstorm conditions[J]. Journal of Chongqing Jiaotong University (Natural Sciences), 2023, 42(6): 32-39. |
| [15] |
孙毅凯, 邹静蓉, 罗大天, 等. 降雨条件下高速公路超高段水流特性仿真研究[J]. 计算机仿真, 2023, 40(12): 186-192. SUN Yikai, ZOU Jingrong, LUO Datian, et al. Study on water flow characteristics of superelevation transition section of freeway under rainfall conditions[J]. Computer Simulation, 2023, 40(12): 186-192. |
| [16] |
MONTGOMERY D R. Road surface drainage, channel initiation, and slope instability[J].
Water Resources Research, 1994, 30(6): 1925-1932.
|
| [17] |
骆保国, 陈旭, 李旭华, 等. 基于Fluent仿真的宽幅路面排水路径长度与水膜厚度研究[J]. 广东公路交通, 2024, 50(3): 1-8, 14. LUO Baoguo, CHEN Xu, LI Xuhua, et al. Study on drainage path length and water film thickness of wide pavement based on fluent simulation[J]. Guangdong Highway Communications, 2024, 50(3): 1-8, 14. |
| [18] |
吴建军, 袁成松, 周曾奎, 等. 短时强降雨对能见度的影响[J]. 气象科学, 2010, 30(2): 274-278. WU Jianjun, YUAN Chengsong, ZHOU Zengkui, et al. Impact of short term heavy rainfall on the monitoring and forecast of sudden visibility descent[J]. Scientia Meteorologica Sinica, 2010, 30(2): 274-278. |
 2025, Vol. 42
2025, Vol. 42



 ,
,