扩展功能
文章信息
- 武凝雨, 高桂云, 苏海燕, 王澳.
- WU Ningyu, GAO Guiyun, SU Haiyan, WANG Ao
- 公路边坡滚石灾害的复合致灾因素分析
- Composite causes analysis on highway slope rockfall hazards
- 公路交通科技, 2025, 42(8): 61-71
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(8): 61-71
- 10.3969/j.issn.1002-0268.2025.08.007
-
文章历史
- 收稿日期: 2024-10-21
近年来,随着基础设施建设的不断推进,山区采石场数量逐渐增加,采石活动频繁,直接导致周边公路边坡的地质环境不断恶化,滚石灾害的发生呈现出高频次、强突发性的特点。部分采石场在靠近交通主干道或乡村公路的地段开展露天开采,受地形、地质及人为扰动等因素的共同作用,边坡稳定性明显下降,严重威胁道路通行安全与沿线居民生命财产安全[1]。
滚石灾害是指岩体或岩块在重力作用下脱离母体后沿坡面滚落的过程,常以崩塌、滑移等形式伴随发生。该类灾害具有突发性强、运动路径不可控、破坏力大等特点,对山区公路尤其危险[2]。在雨季、地震或强烈人类活动(如采石爆破)影响下,滚石灾害更易发生。滚石一旦进入道路区域,轻则阻断交通,重则造成车辆损毁甚至人员伤亡。因此,科学地评估滚石灾害的致灾风险,对于道路沿线的防灾减灾与风险预警具有重要意义[3]。滚石致灾风险的形成通常是多种因素耦合作用的结果。这些致灾因素包括地形地貌、岩体结构、气象水文、植被状况及人为活动等,彼此之间存在复杂的交互关系。目前,滚石危险性评价已从传统的定性研究逐步发展为集成多源信息的定量化分析。研究表明,评价结果的科学性与所选评价单元、指标体系和方法密切相关[4]。叶四桥[5]基于AHP-Fuzzy法,选择地形地貌、地层岩性、气象水文等5个指标作为评价因素,对危岩体的危险性进行了评价。高永才[6]基于层次分析法对云台山景区危岩体和边坡的危险性进行分析,确定影响落石致灾可能性的6种主要因素为:坡度、坡长、落石形状、落石质量和距离。林镇[7]设置危石条件、地形条件、坡表条件4个上层评价指标,采用层次分析法对公路边坡滚石灾害进行风险评估。曾文俊[8]选定自然环境条件、作业环境条件以及管理环境条件3项指标对广西地区露天采石场的风险分级进行了研究。王琦[9]对贵州省松桃县和平社区长冲组危岩体进行了稳定性分析和危害性预测。凌斯祥[10]对上木江坪高陡斜坡危岩体的崩塌落石对都四铁路和G350国道的危险性与定量风险进行了研究。
与此同时,国外许多学者也对滚石进行了相关研究。Stoffel[11]对长时间序列数据进行分析,探究了气候变暖与滚石灾害发生频率和规模的关系。Tiranti[12]提出了一种基于统计交叉分析环境因素的方法,绘制了区域易感性地图,进而应用于初步的滚石风险评估。Silveira[13]通过对高陡斜坡危岩体进行研究,实现了对斜坡崩塌落石运动轨迹的模拟、危害范围与危险性分区的定量评估,以及对道路车辆遇到落石风险的评估,但研究未提供具体的案例数据或实施效果,对于系统的实际应用和效果展示有所欠缺。
目前,关于滚石的研究虽然有很多,但大多集中于滚石本身运动特性的研究,研究强调滚石的形状、体积、数量和运动轨迹等[14]。对于滚石运动造成的地质灾害则往往与崩塌、滑坡等灾害混合研究,滚石灾害单体带来的人员伤亡与造成的财产损失常常被忽视。因此,采用合适的方式对滚石复合因素危险性进行分析存在一定的价值与困难[15-16]。
综上所述,本研究采用层次分析法结合能客观反映各指标致灾贡献的灾害熵模型,对龙响山采石场进行滚石危险性评价。评价体系包括危石条件、坡表条件、坡体条件和其他条件4项上层指标,危石粒径、危石形状、危石坚硬程度等13项下层指标。基于龙响山采石场滚石灾害背景,提出了滚石灾害的复合致灾因素,并对其危险性进行系统分析。设置了红、橙、黄、蓝4个危险性等级,通过灾害现场模拟还原,评估了等级划分的可行性,为复合因素滚石灾害的危险性分析提供了一种有效方法。
1 复合致灾因素敏感性分析根据研究区相关资料分析,滚石灾害的危险性受多种因素共同影响,选择4个上层评价指标:危石条件、坡表条件、坡体条件和其他条件。具体下层评价指标包括:危石粒径、危石形状、危石坚硬程度、危石密度、坡表植被覆盖程度、坡表起伏程度、坡表组成材质、边坡坡度、边坡高度、边坡长度、不良地质现象、不良天气现象和人类工程扰动,共计13项。
1.1 危石条件危石的相关特征直接影响其运动状态,进而对公路的安全产生重大影响。危石的粒径与其体积密切相关,不同体积的危石具有不同的初始动能和在运动过程中受到阻碍的程度。当危石体积较大且处于公路上方时,其动能增加,滚落过程中可能对公路设施、车辆和行人造成更大的威胁。
危石的形状也显著影响其运动状态。近似球状和长棱状的危石在坡表运动时主要表现为弹跳和滚动,受到的坡表阻力较小,这意味着它们更容易越过障碍并到达公路表面。而长柱状和片状的危石则主要以滑动方式运动,受到的坡表阻力较大,尽管这种形状的危石可能较难长距离滚动,但一旦发生滚动,仍然可能在道路附近造成显著破坏[17]。
此外,危石的坚硬程度直接影响其在运动过程中的完整性。硬度较低的危石容易在运动中解体分散,导致动能急剧减小,从而降低对公路的威胁;然而,硬度较高的危石不易破碎,具有较强的反弹能力,更容易越过防护设施直接威胁公路的安全,增加了滚石灾害发生的风险[18]。
危石的密度也是一个关键因素,直接影响其质量。相同体积下,密度越大的危石其重量和获得的动能也会增加。一旦滚落,这些高密度的危石可能对公路及其附属设施产生更大的冲击力,特别是在下坡段或转弯处,这些区域常是公路滚石灾害的高发地段[19]。因此,在设计公路防护措施时,必须充分考虑危石的特征,以减少其对公路安全的潜在威胁。
根据调查,龙响山石场为一座露天开采石灰岩的采石场,造成本次灾害的滚石主要源自采石场内部的一块石料,该石料密度约为2.66 g/cm3,长约1.6 m,宽约1.2 m,厚度约0.8 m,整体呈长棱状。
1.2 坡表条件坡表植被覆盖程度的不同会显著改变坡表的摩擦系数,不同摩擦系数对滚石能量消耗产生明显影响。植被稀少的区域摩擦系数较低,滚石在这种区域内容易保持较高的动能,增加了滚石到达公路的可能性,从而对公路安全构成更大威胁。相反,植被覆盖较好的区域摩擦系数较高,滚石动能消耗更大,可能在到达公路之前就停止运动,这种情况对公路的影响相对较小。
此外,坡表起伏程度会改变滚石的运动状态。较为平坦的坡表使滚石在运动时能够维持更稳定的速度,增加了对公路设施的冲击力。而坡表起伏较大时,滚石的运动路径不稳定,可能导致滚石提前停止或改变方向,从而影响其最终是否会到达公路。坡表的不同组成成分,如岩石、土壤或沙砾,也会影响滚石的运动冲击强度和运动距离。坚硬的岩石坡表可能导致滚石反弹并延长其运动距离,而松软的土壤坡表则有助于减缓滚石的速度,降低对公路的冲击[20]。
采石场各区域植被覆盖情况如表 1所示,通过分析这些区域的植被覆盖和坡表特征,可以更好地预测滚石灾害对公路的潜在威胁,并为公路沿线的防护措施提供科学依据。在植被覆盖较少且坡表起伏较大的区域,公路更易受到滚石的威胁,因而需要加强防护设计,如增加防护网或设置缓冲台阶,以确保公路的安全通行。
| 区域名称 | 占地面积/hm2 | 植被覆盖情况 |
| 采矿区 | 17.70 | 灌木林地、裸地 |
| 工业场地 | 0.50 | 旱地、灌木林地 |
| 临时堆土场 | 0.10 | 裸地 |
| 生活区 | 0.03 | 旱地 |
| 道路 | 0.30 | 旱地、灌木林地 |
| 空地 | 0.01 | 绿地 |
采矿区大部分裸露,对少量表土剥离后即可进行开采。裸露矿区地表对植被影响较大,严重加剧了水土流失。
1.3 坡体条件较大的边坡坡度和边坡高度会增加滚石获得的向下速度分量,从而显著增强其冲击力。当滚石从高陡的边坡上滚落时,其速度迅速增加,导致其动能和冲击力显著提升。这种情况下,如果滚石最终到达公路,其对公路设施、车辆和行人的破坏力将极大增强,增加了公路灾害的风险。
此外,较长的边坡长度会加大滚石运动中的能量损耗。当滚石沿着长边坡运动时,尽管其初速度可能较高,但由于与坡表的持续摩擦和起伏不平的地形,滚石的能量会逐步减少。这意味着在较长的边坡区域内,滚石到达公路时的动能可能会有所降低,从而减少对公路的冲击力。然而,较长边坡也可能导致滚石轨迹的复杂化,增加滚石不规则运动的可能性,使得其轨迹难以预测[21]。
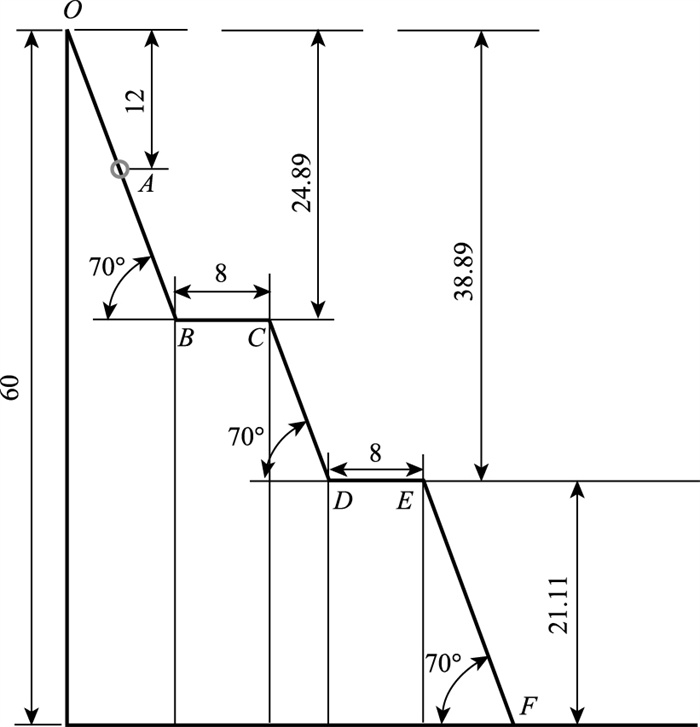
根据现场勘查数据,本次灾害发生于采石场西南工作面的第二台阶处(如图 2,DE段),距离山顶约40 m,距离第一平台(如图 2,BC段)垂直高度约为14 m,距离山脚约为20 m,平台宽8 m,坡脚约70°,如图 2所示。
|
| 图 2 采石场平台示意图(单位:m) Fig. 2 Schematic diagram of quarry platform(unit: m) |
| |
1.4 其他条件
其他地质灾害如滑坡、崩塌等的发生常常会触发滚石运动。这些灾害在公路沿线尤其危险,因为它们不仅会直接破坏道路结构,还可能引发大规模的滚石运动,进一步威胁道路安全。降雨引发的渗流、软化和冲刷作用会不同程度地影响边坡上潜在的危岩和危石,使其更加不稳定[22]。持续的或短期集中的降雨均可能导致滚石灾害的发生,尤其是在降雨量大的山区公路,边坡上的岩石在饱和状态下更容易脱离原位,滚落至公路上,造成交通中断和事故。
此外,人类的开挖和爆破活动往往会加剧危岩和危石的不稳定性,最终引发滚石灾害。在公路建设或维护过程中,若未能充分考虑边坡稳定性,开挖和爆破作业可能削弱岩体的稳定性,导致原本稳固的岩石结构变得脆弱,增加滚石灾害的风险。
根据国际知名气象网站Weather Underground历史天气数据查询统计,南宁市2020年12月整月未发生降雨,武鸣区历年降水量位于广西壮族自治区末位,处在1 500 mm以下。矿区附近近年来未发生过地震。12月5日因挖机发生故障,自下午起石场停止一切生产经营活动。12月5日前石场均正常开挖生产,人类工程活动频繁。
2 复合致灾因素危险性评价 2.1 参量统一性处理各指标具有不同的概念和基本单位,因此它们的重要性无法直接进行比较。为了进行综合评估,需要进行定量转换,将具有不同单位和性质的指标转换为同一数值系统下的评价体系[7]。将各指标划分为4个等级,并对每个等级标准化赋值,具体赋值如表 2所示。
| 评价指标 | 标准化赋值 | |||
| 1 | 2 | 3 | 4 | |
| 危石粒径/m | < 0.05 | [0.05, 0.25) | [0.25, 1) | ≥1 |
| 危石形状 | 片状 | 长柱状 | 长棱状 | 近球状 |
| 危石坚硬程度 | 软岩 | 较软岩 | 较坚硬岩 | 坚硬岩 |
| 危石密度/(g·cm―3) | < 2.25 | [2.25, 2.45) | [2.45, 2.65) | ≥2.65 |
| 坡表植被覆盖程度 | 灌木丛生、乔木发育 | 灌木丛生、少乔木 | 植被稀少、以草为主 | 无植被覆盖 |
| 坡表起伏程度/m | < 0.1 | [0.1, 0.4) | [0.4, 0.7) | ≥0.7 |
| 坡表组成材质 | 黏土性 | 砂土性 | 碎石性 | 岩石性 |
| 边坡坡度/(°) | [0,15) | [15,30) | [30,60) | ≥60 |
| 边坡高度/m | < 3 | [3, 20) | [20, 35) | ≥35 |
| 边坡长度/m | ≥300 | [200,300) | [100,200) | < 100 |
| 不良地质现象发生频次 | 很少发生 | 偶尔发生 | 可能发生 | 频繁发生 |
| 不良天气现象发生频次 | 很少发生 | 偶尔发生 | 可能发生 | 频繁发生 |
| 人类工程扰动发生频次 | 没有或有少量的人类活动 | 少量人类活动且规模小 | 有一定的人类活动 | 大量人类活动,完全直接影响滚石灾害的发生 |
2.2 层次分析法
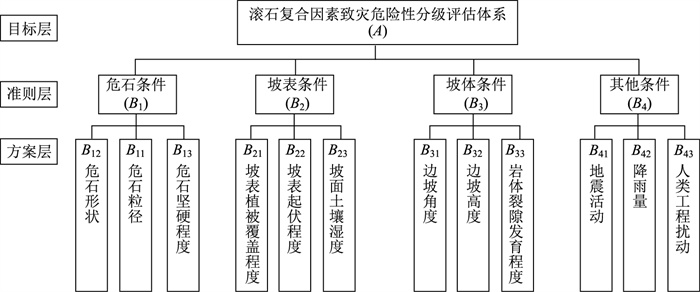
在多层次模型中,目标层A为各指标权重,准则层包含B1~B4共4个指标。其中,准则层B1包括C1~C4共4个下层指标,准则层B2包括C5~C7共3个下层指标,准则层B3包括C8~C10边坡长度,准则层B4包括C11~C13共3个下层指标,如图 3所示。
|
| 图 3 滚石复合因素致灾危险性分级评估体系 Fig. 3 Hierarchical analysis of rockfall composite disaster causes |
| |
采用专家打分法,按1~9标度法构建各指标判断矩阵。
判断矩阵A1,如表 3所示,CR1=0.060 < 0.1,通过一致性检验。
| Ⅰ类评价指标(上层指标) | 危石条件(B1) | 坡表条件(B2) | 坡体条件(B3) | 其他条件(B4) | 权重 |
| B1危石条件 | 1 | 4 | 2 | 5 | 0.447 4 |
| B2坡表条件 | 0.25 | 1 | 0.2 | 2 | 0.112 4 |
| B3坡体条件 | 0.5 | 5 | 1 | 3 | 0.323 5 |
| B4其他条件 | 0.2 | 0.5 | 0.33 | 1 | 0.116 7 |
判断矩阵A2,如表 4所示,CR2=0.044 < 0.1,通过一致性检验。
| Ⅱ类评价指标(危石条件) | 危石粒径(C1) | 危石形状(C2) | 危石坚硬程度(C3) | 危石密度(C4) | 权重 |
| C1危石粒径 | 1 | 4 | 4 | 3 | 0.257 5 |
| C2危石形状 | 0.25 | 1 | 1 | 2 | 0.083 0 |
| C3危石坚硬程度 | 0.25 | 1 | 1 | 2 | 0.083 0 |
| C4危石密度 | 0.33 | 0.5 | 0.5 | 1 | 0.054 9 |
判断矩阵A3,如表 5所示,CR3=0.073 < 0.1,通过一致性检验。
| Ⅲ类评价指标(坡表条件) | 坡表植被覆盖程度(C5) | 坡表起伏程度(C6) | 坡表组成材质(C7) | 权重 |
| C5坡表植被覆盖程度 | 1 | 0.33 | 0.2 | 0.011 9 |
| C6坡表起伏程度 | 3 | 1 | 0.25 | 0.026 6 |
| C7坡表组成材质 | 5 | 4 | 1 | 0.076 8 |
判断矩阵A4,如表 6所示,CR4=0.063 < 0.1,通过一致性检验。
| Ⅳ类评价指标(坡体条件) | 边坡坡度(C8) | 边坡高度(C9) | 边坡长度(C10) | 权重 |
| C8边坡坡度 | 1 | 6 | 8 | 0.242 6 |
| C9边坡高度 | 0.167 | 1 | 3 | 0.055 3 |
| C10边坡长度 | 0.125 | 0.33 | 1 | 0.024 1 |
判断矩阵A5,如表 7所示,CR5=0.047 < 0.1,通过一致性检验。
| Ⅴ类评价指标(其他条件) | 不良地质现象发生频次(C11) | 不良天气现象发生频次(C12) | 人类工程扰动发生频次(C13) | 权重 |
| C11不良地质现象 | 1 | 5 | 7 | 0.060 5 |
| C12不良天气现象 | 0.2 | 1 | 3 | 0.016 1 |
| C13人类工程扰动 | 0.14 | 0.33 | 1 | 0.006 9 |
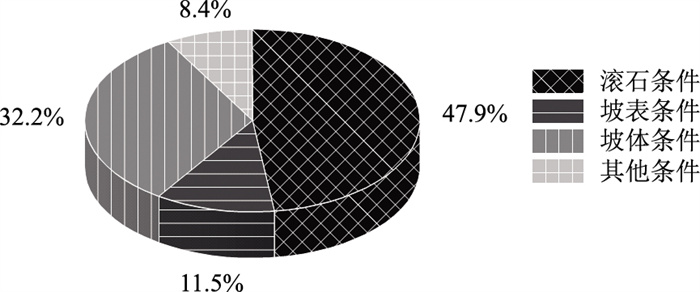
综上,依据层次分析法,各指标权重分布如表 8所示。其中,危石条件对滚石危险性影响最大;坡体条件位于第2;坡表条件权重约占总体的12%,处于第3位;其他条件仅占比8%,位于最后。权重分布如图 4所示。
| 评价指标 | 危石粒径 | 危石形状 | 危石坚硬程度 | 危石密度 | 坡表植被覆盖程度 | 坡表起伏程度 | 坡表组成材质 | 边坡坡度 | 边坡高度 | 边坡长度 | 不良地质现象发生频次 | 不良天气现象发生频次 | 人类工程扰动发生频次 |
| 灾害熵 | 0.736 0 | 0.622 8 | 0.622 8 | 0.736 0 | 0.736 0 | 0.485 5 | 0.736 0 | 0.552 1 | 0.485 5 | 0.736 0 | 0.297 7 | 0.297 7 | 0.622 8 |
| 指标效用值 | 0.263 9 | 0.377 1 | 0.377 1 | 0.263 9 | 0.263 9 | 0.514 4 | 0.263 9 | 0.447 8 | 0.514 4 | 0.263 9 | 0.702 2 | 0.702 2 | 0.377 1 |
| 权重 | 0.049 4 | 0.070 7 | 0.070 7 | 0.049 4 | 0.049 4 | 0.096 4 | 0.049 4 | 0.083 9 | 0.096 4 | 0.049 4 | 0.131 7 | 0.131 7 | 0.070 7 |
|
| 图 4 层次分析法各指标权重占比 Fig. 4 Weight ratio of each indicator with hierarchical analysis method |
| |
计算各区域危险性得分S,计算公式如下:
| $ S=\sum\limits_{i=1}^n W_i \times X_i $ | (1) |
式中,Wi为第i个指标的权重;Xi为第i个指标的得分;n为总的评价指标数。
2.3 灾害熵模型层次分析法提供了一个系统化的框架,通过将复杂问题分解成层次结构,使得问题更加清晰和易于处理。各层次间的相互关系和重要性得以明确,从而便于决策和分析。
熵能反映一个系统的混乱程度,熵越大,系统越混乱。灾害熵模型可以量化各指标的致灾贡献,通过熵的计算,综合考虑多种致灾因素的影响。结合层次分析法,各指标的权重计算和灾害熵模型的应用,可以更全面地反映系统的复杂性和多样性。提高整体评价的精度和准确性, 使得评价结果更具直观性和可解释性。综上所述,层次分析法结合灾害熵模型在复杂系统评价中具有系统性强、定性与定量结合、综合考虑多重因素、提高评价精度、适应性强、结果易于解释和动态分析能力等显著优点。这种组合方法在实际应用中能够有效提升评价的科学性和准确性,为滚石灾害的风险评估提供有力支持。
运用灾害熵对滚石灾害进行危险评价,建立无量纲矩阵M:
| $ \boldsymbol{M}=\left[\begin{array}{cccc} m_{11} & m_{12} & \cdots & m_{1 n} \\ m_{21} & m_{22} & \cdots & m_{2 n} \\ \cdots & \cdots & & \cdots \\ m_{k 1} & m_{k 2} & \cdots & m_{k n} \end{array}\right], $ | (2) |
式中,mij为第i段坡的第j项评价指标标准化的值。
根据式(3)和式(4)确定灾害熵:
| $ F_{i j}=m_{i j} / \sum\limits_{j=1}^n m_{i j}, $ | (3) |
| $ E_j=-\frac{1}{\ln k} \sum\limits_{i=1}^k F_{i j} \ln F_{i j}, $ | (4) |
式中,Fij为第i段坡的第j项评价指标在滚石灾害形成过程中出现的频率;Ej为第j项评价指标的灾害熵,其值越小,表示该指标在滚石灾害形成过程中的贡献越大。
| $ V_j=1-E_j, $ | (5) |
式中,Vj为第j项评价指标的指标效用值,其值越大,表示该指标越重要。
| $ W_j=\frac{V_j}{\sum\limits_{j=1}^k V_j}, $ | (6) |
| $ P_i=\sum\limits_{j=1}^n W_j m_{i j}, $ | (7) |
式中,Pi代表危险性,其值越大,表示该段发生滚石灾害的可能性越大;Wj为第j项评价指标的权重。
根据实际情况结合表 2,得出
| $ \boldsymbol{M}=\left[\begin{array}{lllllllllllll} 4 & 3 & 3 & 4 & 4 & 3 & 4 & 4 & 3 & 4 & 1 & 1 & 3 \\ 4 & 3 & 3 & 4 & 4 & 1 & 4 & 1 & 1 & 4 & 1 & 1 & 3 \\ 4 & 3 & 3 & 4 & 4 & 3 & 4 & 4 & 3 & 4 & 1 & 1 & 3 \\ 4 & 3 & 3 & 4 & 4 & 1 & 4 & 1 & 1 & 4 & 1 & 1 & 3 \\ 4 & 3 & 3 & 4 & 4 & 3 & 4 & 4 & 3 & 4 & 1 & 1 & 3 \end{array}\right] \text { 。} $ |
计算可得Ej、Wj实际值如下(小数点后保留2位):
| $ \begin{array}{l} {E_j} = [\begin{array}{*{20}{c}} {0.74}&{0.62}&{0.62}&{\begin{array}{*{20}{c}} {0.74}&{0.74}&{0.49}&{0.74} \end{array}} \end{array}\\ \begin{array}{*{20}{c}} {}&{}&{0.55}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {0.49}&{0.74} \end{array}}&{0.30}&{0.30}&{0.62} \end{array}} \end{array}], \end{array} $ |
| $ \begin{array}{l} {E_j} = [\begin{array}{*{20}{c}} {0.05}&{0.07}&{0.07}&{\begin{array}{*{20}{c}} {0.05}&{0.05}&{0.10}&{0.05} \end{array}} \end{array}\\ \begin{array}{*{20}{c}} {}&{}&{0.0}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {0.10}&{0.05} \end{array}}&{0.13}&{0.13}&{0.07} \end{array}} \end{array}]。\end{array} $ |
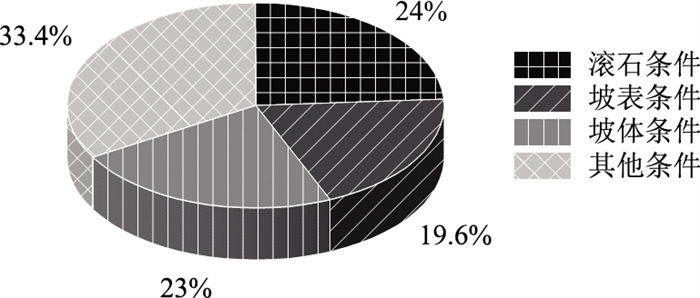
具体数据如表 8所示,其中其他条件权重占比最大,滚石条件和坡体条件次之,坡表条件占比最小,如图 5所示。
|
| 图 5 灾害熵模型各指标权重占比 Fig. 5 Weight ratio of each indicator with disaster entropy model |
| |
2.4 危险性评价结果对比
风险等级的划分需要避免主观判断,自然断点法通过算法自动确定断点位置,减少了人为选择分类标准所带来的主观偏差。这使得分类结果更加客观和一致。自然断点法是一种旨在将一组数值优化排列为“自然”类的分级方法,目前常用于统计地理空间中各类要素的自然分界[23]。该方法基于聚类分析中的单变量分类原理,在分级数确定的情况下,通过迭代计算类间的数据断点,使类中的差异最小化,类间的差异最大化,从而对数据中的相似值进行最恰当的分组。
利用层次分析法计算得出,龙响山采石场滚石灾害危险性数值为2.622 7~3.514 6,基于自然断点法,将危险性分为4个等级,分别对应蓝、黄、橙、红4个等级,危险性逐级递增。
利用灾害熵模型得出,龙响山采石场滚石灾害危险性数值为2.166 7~2.804 6,利用自然断点法,将危险性分为4个等级如表 9所示。
| 等级划分 | 致灾危险性评估 | 层次分析法危险指数 | 灾害熵模型危险指数 |
| 蓝色 | 在该区域滚石灾害基本不可能发生,危险性低,不必采取额外技术和预防措施 | 2.62≤Pi<2.87 | 2.17≤Pi<2.33 |
| 黄色 | 在该区域滚石灾害有可能发生,危险性较低,需进行监控,对相关地区采取一定措施 | 2.87≤Pi<3.10 | 2.33≤Pi<2.51 |
| 橙色 | 在该区域滚石灾害很有可能发生,危险高,需高度重视,建议规避,采取有效措施 | 3.10≤Pi<3.37 | 2.51≤Pi<2.67 |
| 红色 | 在该区域滚石灾害极有可能发生,危险极高,必须高度重视且规避,必须采取有效措施 | 3.37≤Pi≤3.51 | 2.67≤Pi≤2.88 |
这些评估结果的适用性主要局限于龙响山采石场的特定地理和环境条件。自然断点法在这种背景下能够有效减少人为判断的主观性,使分级更加客观和一致,但其结果主要反映了龙响山区域内的滚石灾害风险特征,适用于当地的风险管理。因此,在其他区域应用这些评估方法时,仍需结合当地的实际情况和地质特征进行调整和补充,以确保风险评估的准确性和针对性。
综合层次分析法和灾害熵模型,得到最终危险性分级标准如表 10所示。
| 灾害熵模型危险性等级 | 层次分析危险性等级 | |||
| 红色 | 橙色 | 黄色 | 蓝色 | |
| 红色 | 红色 | 橙色 | 黄色 | 蓝色 |
| 橙色 | 橙色 | 橙色 | 黄色 | 蓝色 |
| 黄色 | 黄色 | 黄色 | 黄色 | 蓝色 |
| 蓝色 | 蓝色 | 蓝色 | 蓝色 | 蓝色 |
表 11为各段(OB段、CD段、EF段、BC段、DE段)的评分(0~1分)。
| 指标 | OB段评分 | CD段评分 | EF段评分 | BC段评分 | DE段评分 |
| 危石粒径/m | 0.70 | 0.75 | 0.72 | 0.65 | 0.68 |
| 危石形状 | 0.60 | 0.65 | 0.62 | 0.58 | 0.60 |
| 危石坚硬程度 | 0.65 | 0.68 | 0.64 | 0.62 | 0.63 |
| 危石密度/(g·cm―3) | 0.55 | 0.60 | 0.57 | 0.54 | 0.56 |
| 坡表植被覆盖程度 | 0.60 | 0.62 | 0.61 | 0.57 | 0.58 |
| 坡表起伏程度/m | 0.52 | 0.55 | 0.54 | 0.50 | 0.51 |
| 坡表组成材质 | 0.50 | 0.52 | 0.51 | 0.48 | 0.49 |
| 边坡坡度/(°) | 0.45 | 0.47 | 0.46 | 0.44 | 0.45 |
| 边坡高度/m | 0.50 | 0.53 | 0.51 | 0.49 | 0.50 |
| 边坡长度/m | 0.55 | 0.58 | 0.56 | 0.53 | 0.54 |
| 不良地质现象发生频次 | 0.40 | 0.42 | 0.41 | 0.38 | 0.39 |
| 不良天气现象发生频次 | 0.45 | 0.46 | 0.44 | 0.42 | 0.43 |
| 人类工程扰动发生频次 | 0.50 | 0.52 | 0.51 | 0.48 | 0.49 |
将每个指标的效用值计算如下。效用值是根据指标的评分与最大评分的比值计算的:
| $ U=\frac{S}{S_{\max }}, $ | (8) |
式中,U为效用值;S为评分;最大评分Smax为1。
层次分析法危险性指数是通过将每个指标的效用值与权重相乘并求和得到的:
| $ R I=\sum(U \times \omega), $ | (9) |
式中,RI为危险性指数;ω为权重。根据每个分段的效用值和权重,可以计算出每个分段的层次分析法(AHP)危险性指数。如表 12所示。根据灾害熵模型,得出各段的效用值,如表 13所示。
| 分段 | 层次分析法危险性指数 |
| OB段 | 3.45 |
| CD段 | 3.40 |
| EF段 | 3.37 |
| BC段 | 3.15 |
| DE段 | 3.20 |
| 评价指标 | OB段效用值 | CD段效用值 | EF段效用值 | BC段效用值 | DE段效用值 |
| 危石粒径/m | 0.263 9 | 0.289 9 | 0.277 8 | 0.252 1 | 0.268 1 |
| 危石形状 | 0.377 1 | 0.368 4 | 0.381 3 | 0.345 1 | 0.362 3 |
| 危石坚硬程度 | 0.348 5 | 0.352 2 | 0.339 5 | 0.323 5 | 0.351 7 |
| 危石密度/(g·cm―3) | 0.263 9 | 0.291 7 | 0.272 6 | 0.285 3 | 0.270 0 |
| 坡表植被覆盖程度 | 0.285 0 | 0.303 1 | 0.267 5 | 0.296 4 | 0.281 6 |
| 坡表起伏程度/m | 0.514 4 | 0.472 1 | 0.489 4 | 0.490 3 | 0.483 9 |
| 坡表组成材质 | 0.263 9 | 0.291 7 | 0.276 2 | 0.266 9 | 0.274 5 |
| 边坡坡度/(°) | 0.447 8 | 0.455 5 | 0.461 4 | 0.475 9 | 0.464 2 |
| 边坡高度/m | 0.514 4 | 0.497 3 | 0.510 1 | 0.478 2 | 0.492 3 |
| 边坡长度/m | 0.263 9 | 0.288 3 | 0.302 0 | 0.273 4 | 0.262 7 |
| 不良地质现象发生频次 | 0.702 2 | 0.680 5 | 0.698 7 | 0.715 2 | 0.663 9 |
| 不良天气现象发生频次 | 0.702 2 | 0.725 9 | 0.691 5 | 0.732 6 | 0.701 1 |
| 人类工程扰动发生频次 | 0.377 1 | 0.394 3 | 0.406 9 | 0.420 5 | 0.389 7 |
对于每个分段,灾害熵模型危险性指数的计算是通过每个评价指标的灾害熵、效用值和权重的加权求和得到的:
| $ R=\sum\limits_{i=1}^n\left(H_{\mathrm{d} i} \times U_i \times \omega_i\right), $ | (10) |
式中,R为加权结果;Hd为灾害熵。由此计算出灾害熵模型危险性指数,如表 14所示。
| 分段 | 灾害熵模型危险性指数 |
| OB段 | 2.74 |
| CD段 | 2.71 |
| EF段 | 2.68 |
| BC段 | 2.55 |
| DE段 | 2.60 |
综上,各区域滚石灾害危险性指数如表 15所示。
| 分段 | 层次分析法危险性指数 | 灾害熵模型危险性指数 | 危险性等级 |
| OB段 | 3.45 | 2.74 | 红色 |
| CD段 | 3.40 | 2.71 | 红色 |
| EF段 | 3.37 | 2.68 | 红色 |
| BC段 | 3.15 | 2.55 | 橙色 |
| DE段 | 3.20 | 2.60 | 橙色 |
勘察发现距山顶12 m处有塌方迹象。坡面经过工程改造起伏程度较小,矿区整体裸露,水土流失严重。
综上,根据现场事故情况,分析计算得到OB段、CD段、EF段为红色危险等级,BC段、DE段为橙色危险等级,如图 6所示。

|
| 图 6 灾害熵模型危险性分级(单位: m) Fig. 6 Risk classification with disaster entropy model (unit: m) |
| |
3 滚石灾害危险性分析及公路安全评估 3.1 灾害现场地质条件与人类工程活动对滚石灾害的影响
在采石场的勘察过程中,发现山顶附近12 m的坡面处存在明显的塌方迹象。该区域的坡面经过工程改造后,虽然坡度有所减小,起伏程度较小,但整体矿区仍然是裸露的状态,水土流失问题严重。这一地质环境使得岩石和土体易于松动,从而加大了滚石灾害发生的可能性,尤其在极端天气条件或高强度的采石作业下,松动的岩石和土壤极易发生滑移或滚落。
矿区的裸露状态和水土流失现象导致坡面稳定性较差。坡面一旦失去稳定,表土和岩石便会松动并发生滑坡或滚落。在大雨天气条件下,由于雨水渗透作用,土壤含水量增加,导致坡体的抗力降低,从而加剧了滚石的发生频率。在采石活动高峰期,大型机械操作和爆破作业也会对矿区周围的地质结构产生扰动,进一步影响坡面稳定性。因此,采石作业的震动、机械作业的扰动及水土流失的交互作用,形成了滚石灾害发生的机制。
3.2 滚石灾害危险性预警分析根据现场实际情况反馈,灾害发生时,场长正在碎石机大机口位置巡查,听见西南工作面方向传来巨大声响。前去探查发现一石块砸中第2台阶上的一台等待维修的挖掘机,挖掘机驾驶室被砸扁,驾驶员趴在驾驶座位上,头部出血,呼唤无反应。
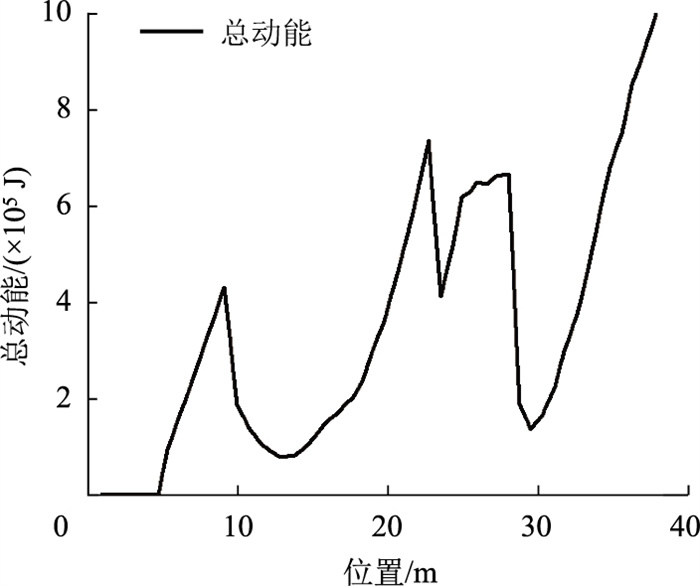
根据前述监测与预警指标的计算分析,边坡的AB段和CD段被划定为滚石灾害红色预警区域,而BC段和DE段则为黄色预警区域。为了进一步验证层次分析法和灾害熵模型的准确性,我们结合矿区的实际数据,通过多次重复试验并借助Rocfall软件对滚石运动进行了数值仿真。仿真结果如图 7所示,从仿真图像中可以清晰地看到,在第1台阶(BC段)和第2台阶(DE段)区域,滚石的动能出现了明显的下降或动能增量减小的趋势。根据这一现象,我们将这些区域的预警等级划定为橙色,表明这些区域相比矿区其他区域的滚石失稳危险性有所降低,滚石的冲击力也相应减小。
|
| 图 7 采石场滚石总动能变化 Fig. 7 Variation of total kinetic energy of rockfall in quarry |
| |
然而,尽管这些区域的滚石动能有所减弱,依然存在沿坡面继续滚落的可能性,特别是在黄色和橙色预警区间的区域。虽然仿真结果表明这些区域的滚石风险相对较低,但其仍然对公路安全带来潜在威胁。仿真显示,部分滚石可能会翻越台阶,继续下滑并滚落至公路上,从而对公路造成影响。这一现象表明,滚石的运动不仅受坡面角度、岩石硬度和土壤湿度等因素影响,还受坡面细节和局部地质结构的影响,因此对这些区域的评估仍需要保持警惕。
3.3 公路安全隐患与防护措施建议根据仿真结果与实际灾害案例,AB段和CD段位于红色预警区域,滚石易失稳发生滚落,且滚石运动带来的冲击力比橙色区间明显增大。这些高风险区域距离公路较近,一旦发生滚石灾害,将对公路交通安全造成严重威胁,甚至可能导致交通中断和重大事故。因此,对于这些高风险区域,必须采取更为严格的防护措施。
(1) 坡面防护措施:在AB段和CD段区域,建议采取更为有效的坡面防护措施,例如:在坡面上安装防护网、加固支撑结构或者设置固定的岩石锚固系统,以防止松动的岩石进一步滚落。
(2) 公路防护设施升级:公路沿线应增设滚石拦截设施,如防石网、防护墙和警示标志等,并在公路沿线的关键部位安装防撞栏杆。这些设施可以有效地拦截或减缓滚石的速度,降低事故发生的概率。
(3) 灾害预警系统提升:基于层次分析法和灾害熵模型的结果,可以进一步提升现有的滚石灾害预警系统。通过结合实时数据监测、气象预测以及采石活动的动态信息,建立更加精确的预警模型,提前识别潜在的滚石危险,并采取应急措施。
(4) 定期巡查与地质监测:建议在高风险区域内进行定期巡查,特别是在采石作业期间或者恶劣天气来临前,加强对矿区周围地质变化的监测,及时发现地质异常并采取应对措施。
对于BC段和DE段,尽管仿真结果显示这些区域的滚石动能有所减小,但由于它们位于黄色预警区间,仍然需要保持适当的防护措施,避免滚石对公路造成潜在威胁。因此,建议定期检查这些区域的防护设施,及时清理坡面杂草,减少雨水渗透。
4 结论本研究通过结合层次分析法和灾害熵模型,系统地评估了广西龙响山采石场的滚石灾害危险性,特别关注了采石场与相邻公路之间的安全隐患。通过数值仿真和实际灾害数据验证了前述模型的有效性,研究的主要结论如下。
(1) 基于层次分析法和灾害熵模型的计算,研究将采石场的边坡分为红色和黄色2种预警区域。AB段和CD段被划定为红色预警区域,具有较高的滚石失稳风险,而BC段和DE段则为黄色预警区域,滚石风险相对较低。这一划分结果与实际监测数据及灾害案例相符,验证了方法在危险性评估中的有效性和可靠性。
(2) 利用Rocfall软件对滚石运动进行了数值仿真,进一步验证了危险性评估结果。在BC段和DE段,仿真结果显示滚石的动能出现明显下降或增量减小的趋势,证实了这2个区域的滚石风险低于其他区域。这表明,尽管这些区域滚石的动能有所减弱,但依然存在潜在的威胁,特别是对矿区公路的安全影响不容忽视。
(3) 本研究的创新之处在于将层次分析法与灾害熵模型相结合,综合考虑了多种影响滚石灾害的因素,提出了一种基于多因素综合评价的滚石灾害危险性分析方法。该方法不仅适用于矿区内的滚石风险评估,还能根据不同地质条件和采石活动的特点灵活调整评估指标和权重,具有较强的适用性和可操作性。此外,结合数值仿真与实际灾害案例的分析,为矿区公路的安全防护提供了切实可行的建议,并为类似地区的滚石灾害评估提供了参考。
(4) 本研究成果为矿区滚石灾害的预警和防护提供了科学依据,尤其是在考虑到矿区与公路相邻的地理背景下,提出的防护措施具有较高的实用价值。研究表明,即使在滚石动能较低的区域,滚石依然可能对公路安全构成威胁,强调了综合防护措施的重要性。该方法可为类似地区的滚石灾害评估与防护规划提供借鉴,并对促进灾害管理与风险控制有着积极的推动作用。
| [1] |
解开华, 唐可, 吴谦, 等. 戈壁盐渍土地区水泥稳定碎石材料宏微观特性分析[J]. 公路交通科技, 2025, 42(2): 68-77. XIE Kaihua, TANG Ke, WU Qian, et al. Macro and micro characteristics of cement stabilized macadam in gobi saline soil area[J]. Journal of Highway and Transportation Research and Development, 2025, 42(2): 68-77. DOI:10.3969/j.issn.1002-0268.2025.02.008 |
| [2] |
KARWOWSKI W, MITAL A. Applications of fuzzy set theory in human factors[M].
Amsterdam: Elsevier, 1986.
|
| [3] |
胡厚田. 成昆线共和—尼日岩质边坡崩塌落石强度等级预测的研究[J]. 西南交通大学学报, 1989, 2(1): 52-59. HU Houtian. The study of prediction ot landfalls and rockfalls of rock slopes from Gonghe to Niri on Chengdu-Kunming railway[J]. Journal of Southwest Jiaotong University, 1989, 2(1): 52-59. |
| [4] |
KROESE D P, BRERETON T, TAIMRE T, et al. Why the monte carlo method is so important today[J].
WIREs Computational Statistics, 2014, 6(6): 386-392.
DOI:10.1002/wics.1314 |
| [5] |
叶四桥, 唐红梅, 祝辉. 基于AHP-Fuzzy方法的危岩危险度评价[J]. 武汉理工大学学报(交通科学与工程版), 2006, 30(5): 800-803. YE Siqiao, TANG Hongmei, ZHU Hui. Dangerous degree estimation of perilous rock based on AHP-Fuzzy method[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2006, 30(5): 800-803. DOI:10.3963/j.issn.2095-3844.2006.05.016 |
| [6] |
高永才. 云台山景区危岩体、边坡风险性评价及预警研究[D]. 焦作: 河南理工大学, 2014. GAO Yongcai. Risk assessment and early warning study of perilous rocks and slopes in Yuntai Mountain scenic region [D]. Jiaozuo: Henan Polytechnic University, 2014. |
| [7] |
林镇. 公路边坡滚石灾害运动特征模拟及风险评估[D]. 福州: 福州大学, 2015. LIN Zhen. Motion characteristic simulation and risk assessment for rockfall disaster of highway slope [D]. Fuzhou: Fuzhou University, 2015. |
| [8] |
曾文俊. 广西地区中小型露天采石场风险分级管控实践研究[D]. 南宁: 广西大学, 2017. ZENG Wenjun. Research on the security status of small and medium-sized outdoor quarry in Guangxi Region and the practice of risk grading and control [D]. Nanning: Guangxi University, 2017. |
| [9] |
王琦, 胡亚净, 宋伟利, 等. 岩溶山区危岩稳定性分析及危害性预测: 以贵州松桃县长冲危岩体为例[J]. 中国地质灾害与防治学报, 2023, 34(1): 75-84. WANG Qi, HU Yajing, SONG Weili, et al. Stability analysis and hazard prediction of dangerous rock masses in karst mountainous area: A case study of Changchong dangerous rock mass in Songtao County, Guizhou Province[J]. The Chinese Journal of Geological Hazard and Control, 2023, 34(1): 75-84. |
| [10] |
凌斯祥, 李乐, 石奥博, 等. 上木江坪高陡斜坡危岩特征与定量风险评估[J]. 工程地质学报, 2024, 32(3): 1083-1097. LING Sixiang, LI Le, SHI Aobo, et al. Development characteristics and quantitative risk assessment of dangerous rocks exit high-steep Shangmujiangping hillslope at mountain transportation corridor[J]. Journal of Engineering Geology, 2024, 32(3): 1083-1097. |
| [11] |
STOFFEL M, TRAPPMANN D G, COULLIE M I, et al. Rockfall from an increasingly unstable mountain slope driven by climate warming[J].
Nature Geoscience, 2024, 17(3): 249-254.
DOI:10.1038/s41561-024-01390-9 |
| [12] |
TIRANTI D, MALLEN L, NICOLÒ G. Rockfall hazard estimation and related applications for a preliminary risk assessment at regional scale: An example from northwestern Italian Alps[J].
Landslides, 2023, 20(8): 1691-1704.
DOI:10.1007/s10346-023-02060-4 |
| [13] |
SILVEIRA L R C, LANA M S, DOS SANTOS T B. A quantitative rockfall risk analysis system for highway rock slopes[J].
Geotechnical and Geological Engineering, 2024, 42(2): 1131-1152.
DOI:10.1007/s10706-023-02609-z |
| [14] |
JABOYEDOFF M, LABIOUSE V. Preliminary assessment of rockfall hazard based on GIS data [C]// Proceedings of 10th International Congress on Rock Mechanics. Lisbon: ISRM, 2003: 575-578.
|
| [15] |
AZZONI A, LA BARBERA G, ZANINETTI A. Analysis and prediction of rockfalls using a mathematical model[J].
International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1995, 32(7): 709-724.
|
| [16] |
赵勇, 张锐, 邢学敏, 等. 基于SBAS-InSAR技术的膨胀土边坡变形失稳特征[J]. 公路交通科技, 2024, 41(8): 22-30. ZHAO Yong, ZHANG Rui, XING Xuemin, et al. Deformation instability characteristics of expansive soil slope based on SBAS-InSAR technique[J]. Journal of Highway and Transportation Research and Development, 2024, 41(8): 22-30. DOI:10.3969/j.issn.1002-0268.2024.08.003 |
| [17] |
丁浩江, 张广泽, 岳志勤. 坪上隧道口危岩落石失稳模式及运动特征分析[J]. 铁道工程学报, 2015, 32(12): 7-11, 29. DING Haojiang, ZHANG Guangze, YUE Zhiqin. Analysis of unstable models and movement characteristics of unstable rockfall at Pingshang tunnel entrance[J]. Journal of Railway Engineering Society, 2015, 32(12): 7-11, 29. |
| [18] |
刘伟鹏, 毛邦燕. 基于发生概率和致灾性的危岩落石灾害风险评价[J]. 铁道勘察, 2018, 44(6): 47-53. LIU Weipeng, MAO Bangyan. Risk assessment of rockfall disaster based on probability of occurrence and catastrophic characteristics[J]. Railway Investigation and Surveying, 2018, 44(6): 47-53. |
| [19] |
赵秋林. 兰渝铁路范家坪隧道出口危岩落石分析及防护设计[J]. 铁道标准设计, 2017, 61(10): 137-140. ZHAO Qiulin. Analysis and protection design of Fanjiaping tunnel exit rockfall on Lanzhou-Chongqing railway[J]. Railway Standard Design, 2017, 61(10): 137-140. |
| [20] |
相志强. 高陡边坡隧道洞口段危岩落石灾害防护技术[D]. 成都: 西南交通大学, 2013. XIANG Zhiqiang. Preventive technology of unstable rock and rockfall hazard at tunnel entrance in high and steep slope [D]. Chengdu: Southwest Jiaotong University, 2013. |
| [21] |
郭书云. 石太线路基边坡危岩落石整治方案研究[J]. 铁道标准设计, 2014, 58(2): 4-7. GUO Shuyun. Research on treatment scheme of perilous rocks and falling rocks for protecting subgrade slope of Shijiazhuang-Taiyuan railway[J]. Railway Standard Design, 2014, 58(2): 4-7. |
| [22] |
苏永攀, 郑佳乐, 陈飞, 等. 降雨条件下双层滑面滑坡时程稳定性分析[J]. 公路交通科技, 2024, 41(8): 96-105. SU Yongpan, ZHENG Jiale, CHEN Fei, et al. Time-history stability analysis on double-layer sliding surface landslide under rainfall[J]. Journal of Highway and Transportation Research and Development, 2024, 41(8): 96-105. DOI:10.3969/j.issn.1002-0268.2024.08.010 |
| [23] |
黄起, 李敬平, 郑峥, 等. 自然断点法在材料设备分类分级管理评价体系中的应用[J]. 住宅与房地产, 2023(11): 44-48. HUANG Qi, LI Jingping, ZHENG Zheng, et al. Application of natural breakpoint method in classification and grading management evaluation system of materials and equipment[J]. Housing and Real Estate, 2023(11): 44-48. |
 2025, Vol. 42
2025, Vol. 42



 ,
,