扩展功能
文章信息
- 尚晶, 闫学东, 向韵巧, 陈立峰, 何庆.
- SHANG Jing, YAN Xuedong, XIANG Yunqiao, CHEN Lifeng, HE Qing
- 考虑乘客路径分配的模块化公交运行线路优化设计
- Optimal design on modular bus operating lines considering passenger paths assignment
- 公路交通科技, 2025, 42(8): 27-34
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(8): 27-34
- 10.3969/j.issn.1002-0268.2025.08.003
-
文章历史
- 收稿日期: 2023-10-12
2. 北京交通大学 交通运输学院, 北京 100044
2. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China
交通运输作为人和货物联系的纽带,实现了社会和经济的互动[1]。然而,机动化的快速发展致使汽车拥有量迅速增长、出行需求日益增多、交通拥堵状况不断加重。促进以公共交通为导向的城市发展战略、推动城市交通与土地利用优化整合,是改善上述问题的有效手段[2-3]。2020年《中国交通的可持续发展》白皮书指出,发展公共交通是加强城市交通治理、提升城市居民生活品质的有效措施[4]。Ceder[5]在全球17个城市开展对比测试发现,使用公共交通代替私家车出行能够使道路车辆减少近50%。由此可见,发展公共交通是应对城市机动化负面效应的良策。
根据中国交通运输部发布的《2024年交通运输行业发展统计公报》显示,在2024年全国城市客运量按照运输方式的统计中,公共汽电车运输的客运量占比为74.1%[6]。由此可见,公交在公共交通系统中占据重要地位[7]。然而,当前传统公交存在载运设备分配不合理导致供求不匹配、直达率低导致换乘增多、换乘等待时间过长影响出行总时间等问题,这些问题共同导致了公交运营成本和乘客的广义旅行成本增加。模块化公交的诞生为解决上述问题、促进公交可持续发展提供了新思路。模块化公交的拆分组合特性使其能够在运行线重合段实现途中无缝换乘。该换乘模式消除了传统公交站内换乘所需的换乘等待时间。
模块化公交是近年提出的公交新形式,现阶段主要从其运载工具资源分配角度开展研究。Mahmassani[8]开发了宏观基本图,又名网络基本图(MFD);Dakic[9]将模块化公交优化模型与3D-MFD结合,最终确定了模块化公交的模块最佳组合数量和调度模块的最佳频率;Zhang[10]将模块化公交系统表述为一个整数规划,探究乘客最大化被匹配和网络中车辆行驶总里程最小化;Tian[11]确定了各站点可容纳的模块化单元最大数量。近年来,模块化公交的研究已从理论转移至实践。某运输企业研发的模块化公交实体在运行中的对接性能测试于2018年在迪拜完成,进而验证了途中无缝换乘的可行性。
城市公共交通的路径优化研究起步较早,成果颇丰,为模块化公交的路径优化提供了理论支持。就公交路径优化而言,管德永[12]针对高度分散和随机的客流研究了需求响应型公交车辆调度及路径优化。何民[13]建立了同时考虑响应式定制公交运营商成本最小和乘客出行可靠性、舒适性要求的公交线路设计模型。吴红波[14]提出了基于GIS路径分析和多目标规划的公交车路网优化方法。姚佼[15]提出了考虑不同类型应急车辆调度和最优路径选择的双层规划集成优化模型。奇格奇[16]提出了面向出行者异质化需求的无人驾驶电动公交接驳路径优化方法。就路径优化方法而言,有2种方式出现较早: (1)从一个完整的线路配置中依次删除线路,被淘汰的线路上的乘客被分配到其他线路, (2)在没有线路配置的情景下连续添加在最短路径上的出行线路。
与上述方法不同,Guan[17]在给定公共交通网络、出行需求和运行线路候选集的情景下,根据特定标准在运行线路候选集中筛选运行线路,最终确定公交运行线网。当前针对模块化公交的研究多倾向于模块的配置调度优化,较少从路径优化角度思考模块化公交的运行线路设计和乘客路径分配优化。此外,传统公交的运行线路设计较少考虑乘客路径分配这一因素。然而,为实现途中无缝换乘,模块化公交对运行线路设计提出了路径可达的新要求,因此在进行其运行线路设计时需要考虑乘客路径分配。本研究正是对模块化公交的运行线路设计研究进行了补充,提出了考虑乘客路径分配因素的模块化公交运行线路设计模型,在既定的运行线路候选集中筛选运行线路设计方案,在既定的路径候选集中为已知起讫点对(以下简称“OD对”)选择乘客路径分配方案。本研究中的运行线路和路径均由连续的物理路段组成,由运行线路集储存各条公交运行线,由路径集储存各OD对的路径,一条路径的运输任务可由直达运行线或换乘多条运行线实现。
与传统公交相比,模块化公交不仅能够灵活调配运载工具容量以适应出行需求差异,更通过途中无缝换乘消除了换乘等待时间。本研究针对模块化公交的运行线路设计和路径分配问题,以降低运营成本和乘客广义旅行成本为目标,结合途中无缝换乘特性,构造了考虑乘客路径分配的模块化公交运行线路设计模型,获得了模块化公交的运行线路设计和乘客路径分配方案。
1 问题描述本研究在已知模块化公交网络的物理路段集、乘客路径候选集、运行线路候选集和OD对条件下,基于无缝换乘特性构建考虑乘客路径分配的模块化公交运行线路设计模型,从候选集中筛选符合要求的运行线路集,并确定对应的乘客路径集。
1.1 乘客路径分配客运线路选择可分为路径选择和运行线选择。路径选择方面,每个OD对对应的可选择路径可能有多条,而每位乘客仅可选择一条路径出行,所选路径将决定其绕行情况和车内出行时间。运行线路选择方面,一条路径对应的运行线组合可存在多种,每位乘客仅选择一个运行线组合,所选组合将决定其换乘次数、换乘及换乘等待时间。因此,乘客路径分配问题的目标为减少车内出行时间、换乘及换乘等待时间。
假设模块运行速度、所需换乘及换乘等待时间相同,则车内总出行时间用所有OD对选择的路径总长度表达,换乘及换乘等待时间用所有OD对所选运行线路组合的换乘总数表达。若一个运行线组合包含n条运行线,则换乘次数为n-1,故换乘及换乘等待时间可表达为各OD对所选运行线数目的总和。
1.2 模块化公交运行线路设计方法重点模块化公交可以实现无缝换乘,由此总结传统公交站内换乘和模块化公交途中无缝换乘的区别如下。
(1) 站内换乘由乘客移动实现换乘。途中无缝换乘由运行途中模块组合与拆分实现换乘。
(2) 站内换乘在换乘站进行,要求乘客在换乘站内步行至换乘线路。途中无缝换乘在换乘路段进行,要求乘客由原模块穿越至换乘运行线对应模块。
(3) 站内换乘通常采用双向运行线。途中无缝换乘要求多个模块必须是同向行驶,故采用单向运行线。
提出模块化公交运行线路设计方法重点如下。
(1) 交通网络连通性
模块化公交运行线路设计的关键集合为路段集、运行线路集和路径集。运行线和路径的最小组成单元均是路段。交通网络连通性要求所得运行线路集覆盖所有路段,即每个路段至少被一条运行线经过。
(2) 路径可达性
为确保所有OD对需求均被满足,运行线路要保证所有已被选择的路径均可达。一条路径的候选运行线可能存在多条,故每条路径拥有一个候选运行线路集。为保证每个OD对可达,被选择路径的候选运行线路集要覆盖路径中的全部路段,即路径中的每个路段至少被候选运行线路集中的一条运行线经过。
(3) 途中无缝换乘特性
由于途中无缝换乘在运行线重合路段进行,故每条已被选择路径所选的多条运行线路需要共同覆盖足够数量的换乘路段,即运行线路重合路段数目足够。2种换乘路段构成情况如图 1所示。图 1(a)中的换乘路段组为(1)—(2)和(3)—(4);图 1(b)中的换乘路段组为(1)—(2)—(3)和(4)—(5)。2种情况的运行线路重合路段数目均足够。

|
| 图 1 2种换乘路段构成情况 Fig. 1 Two types of transfer lines |
| |
2 考虑乘客路径分配的模块化公交运行线路设计模型
结合图 1进行运行线路设计和乘客路径分配问题的模型构建,采用Python语言和Gurobi求解器,使用割平面法将模型运用于算例。首先介绍模型的符号定义、描述运行线路设计和乘客路径分配子问题,随后得到完整模型。模型旨在确定给定公交网络上的模块化公交运行线路配置和乘客路径分配。为便于模型公式化,制定假设为:(1)假设OD对需求固定;(2)进一步假设从预先确定的运行线路候选集中选择最佳运行线路配置计划;(3)每个OD对的乘客将从给定的一组候选路径中选择一条路径。
2.1 符号定义本研究决策变量为xm,yrsm,zkrs,均为0-1变量。其中,xm决定了运行线m是否被运行线路网络选择;yrsm决定了运行线m是否被ODrs对选择;zkrs决定了路径k是否被ODrs对选择。符号定义如表 1所示。
| 符号 | 定义 |
| A | 规定路网中的路段集合 |
| M | 规定路网中可行的运行线集合 |
| N | 规定路网中的站点集合 |
| Krs | 从站点r到站点s的可选路径集合 |
| xm | 0-1变量,运行线m是否被运行线路网络选择 |
| yrsm | 0-1变量,运行线m是否被ODrs对选择 |
| zrsk | 0-1变量,路径k是否被ODrs对选择 |
| Δmaij | 0-1矩阵,运行线m是否通过路段aij |
| δrsaijk | 0-1矩阵,ODrs对可选路径k是否通过路段aij; |
| aij | 连接站点i和站点j的路段 |
| laij | 路段aij的长度 |
| drs | 从站点r到站点s的出行需求 |
| α, β, γ | 目标函数的权重因子 |
| fm | 运行线m的频率 |
| Caij | 路段a的单向道路通过能力 |
| Lmax | 运行线的最大长度 |
| Lmin | 运行线的最小长度 |
| T | ODrs对的最大换乘总次数 |
2.2 运行线路设计
双目标中的第1部分为运行线路设计问题,该问题的目标是运营成本最小化。线路设计分析中,公交运营成本主要取决于运行线总长度,运营成本与运行线总长度呈正相关。因此本研究假设各条运行线的服务水平一致,将降低运营成本目标表达为最小化运行线总长度。同时,运行线路设计还要确保交通网络连通性,由此保证任意2个站点之间可达。
2.3 乘客路径分配双目标中的第2部分为乘客路径分配问题,该问题的目标是降低乘客的广义旅行成本。客运线路选择可分为路径选择和运行线选择。乘客所选路径将决定其绕行情况和车内出行时间。乘客所选运行线组合将决定其换乘次数、换乘时间及换乘等待时间。乘客路径分配需要确保路径可达性。同时,要求乘客在运行线路候选集中选择运行线路,且一个OD对的乘客仅选择一条路径。
2.4 考虑乘客路径分配的模块化公交运行线路设计模型运行线路设计子问题和乘客路径分配子问题通过约束条件式(5)耦合,共同构成模型。在式(1)中,
| $ \begin{gather*} \min F(x, y, z)=\alpha \sum\limits_{m \in M} \sum\limits_{a_{i j} \in A} \Delta_{m}^{a_{i j}} l_{a_{i j}} x_{m}+ \\ \beta \sum\limits_{r \in N} \sum\limits_{s \in N} \sum\limits_{m \in M} d_{\mathrm{rs}} y_{\mathrm{rs}}^{m}+\gamma \sum\limits_{r \in N} \sum\limits_{s \in N} \sum\limits_{i \in N} \sum\limits_{j \in N} \sum\limits_{k \in K_{\mathrm{rs}}} \sum\limits_{a_{i j \in A}} d_{\mathrm{rs}} \boldsymbol{\delta}_{\mathrm{rs}}^{a_{i j}{ }^{k}} l_{a_{i j}} z_{\mathrm{rs}}^{k}, \end{gather*} $ | (1) |
| $ \text { s. t. } \quad \sum\limits_{m \in M} \Delta_{m}^{a_{i j}} x_{m} \geqslant 1 \quad \forall a_{i j} \in A, i, j \in N, $ | (2) |
| $ \sum\limits_{m \in M} \Delta_{m}^{a_{i j}} y_{\mathrm{rs}}^{m} \geqslant \boldsymbol{\delta}_{\mathrm{rs}}^{a_{i j} k} z_{\mathrm{rs}}^{k} \quad \forall a_{i j} \in A, k \in K_{\mathrm{rs}}, i, j, r, s \in N, $ | (3) |
| $ \sum\limits_{k \in K_{\mathrm{rs}} a_{i j} \in A} \sum\limits_{m \in M} z_{\mathrm{rs}}^{k} \boldsymbol{\delta}_{\mathrm{rs}}^{a_{i j}{ }^{k}} \Delta_{m}^{a_{i j}} y_{\mathrm{rs}}^{m} \geqslant \sum\limits_{m \in M} y_{\mathrm{rs}}^{m}-1+ \\ \;\;\;\;\sum\limits_{k \in K_{\mathrm{rs}}} \boldsymbol{\delta}_{\mathrm{rs}}^{a_{i}{ }^{k}} z_{\mathrm{rs}}^{k} \quad \forall i, j, r, s \in N, $ | (4) |
| $ x_{m}-y_{r s}^{m} \geqslant 0 \quad \forall m \in M, r, s \in N, $ | (5) |
| $ \sum\limits_{k \in K_{r s}} z_{r s}^{k}=1 \quad \forall r, s \in N, $ | (6) |
| $ \sum\limits_{m \in M} \Delta_{m}^{a_{i j}} f_{m} x_{m} \leqslant C_{a_{i j}} \quad \forall a_{i j} \in A, r, s \in N, $ | (7) |
| $ \left(\sum\limits_{a_{i j} \in A} \Delta_{m}^{a_{i j}} l_{a_{i j}}-L_{\mathrm{max}}\right) x_{m} \leqslant 0 \quad \forall m \in M, i, j \in N, $ | (8) |
| $ \left(\sum\limits_{a_{i j} \in A} \Delta_{m}^{a_{i j}} l_{a_{i j}}-L_{\mathrm{min}}\right) x_{m} \geqslant 0 \quad \forall m \in M, i, j \in N, $ | (9) |
| $ \sum\limits_{m \in M} y_{r s}^{m} \leqslant T \quad \forall r, s \in N_{\circ} $ | (10) |
式(1)中的α,β,γ之和为1;约束条件式(2)确保了每个路段至少被一条运行线覆盖;约束条件式(3)确保了路径可达性;约束条件式(4)基于路径可达性确保了一条路径所选运行线组合的换乘路段数目足够;约束条件式(5)确保了乘客在可选运行线路集中选择运行线路;约束条件式(6)规定了一个OD对的乘客仅选择一条路径;式(7)限制同一时刻出现在同一路段上的车辆数,从而控制车辆在换乘路段的组合数目上限和车辆数不超过道路通过能力;约束条件式(8)规定了运行线最小长度,避免了终点站频繁车辆周转;式(9)限制了运行线最大长度,降低了线路绕行程度,同时降低了过长运行线沿线乘客数量波动较大导致的模块利用效率低下的可能性;约束条件式(10)考虑了乘客间的公平性,限制了各OD对的换乘次数上限。
3 算例分析 3.1 初始运行线路设计将模型运用于算例,检验其可行性。本研究设计了一个包含9个站点、10条路段的简单网络。网络中各站点的可达方向包含单方向和多方向,路段呈现分枝状和环状,路段均为双向道路,故本研究简单网络的整体结构与实际路网相似。由第2章可知,考虑乘客路径分配的模块化公交运行线路设计模型是基于既定路网和既定OD对出行需求,对运行线路候选集和路径候选集进行筛选,最终得到运行线路设计和乘客路径分配结果。本研究根据简单网络的物理连通关系,将路段作为基础单元,由其组合得到运行线和路径。遵照如下原则将基础单元组合成候选运行线和候选路径,得到运行线路候选集和路径候选集。
(1) 为保证路网的连通性,初始设定的运行线路候选集必须覆盖路网的所有物理路段。
(2) 由途中无缝换乘与站点换乘的区别可知,运行线和路径均需要设置为单方向线路。
(3) 为了避免运行线和路径过长而导致的迂回走行过于严重,本研究基于简单路网结构将候选集中的运行线和路径的最大长度设定为6个路段单元。
(4) 为了简化算例规模,本研究将每个OD对的候选路径控制在3条范围内。
算例分析的目的是对模型进行性能测试,检验模型能否得到合理结果。当前模块化公交尚在试验阶段,无实际数据参考,因此,研究结合简单网络对初始解的参数进行简化设定以完成性能测试。其中,权重因子分别为α=0.33,β=0.33,γ=0.33,后续可将目标函数3部分转换为时间价值,进一步转化为可比较的货币成本,并结合实际数据与换乘惩罚得到权重因子在不同场景中的实际值[18];结合简单网络结构,设定运行线最大长度为4 km,最小长度为2 km;每个OD对的出行需求值为5;道路容量值为2;一次出行的换乘次数上限为3次。将得到的运行线路候选集和路径候选集运用于模型,进而在目标函数和约束条件的共同作用下,从运行线路候选集和路径候选集中分别筛选运行线路和路径,得到运行线路配置结果和乘客路径分配结果。(7,2)OD对的运行线路配置结果如图 2所示,运行线路配置及路径分配部分结果如表 2所示。
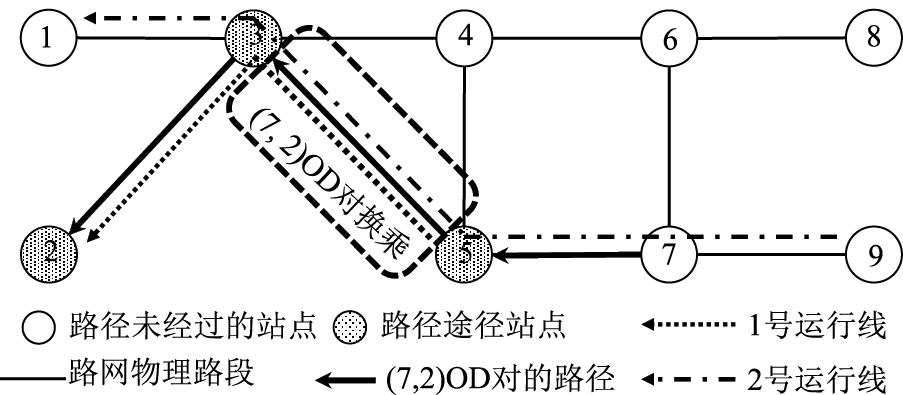
|
| 图 2 (7,2)OD对的运行线路配置结果 Fig. 2 Operating line design result for (7, 2) origin and destination pair |
| |
| OD对 | 换乘次数/次 | 路径 |
| (1, 7) | 0 | ①—③—⑤—⑦ |
| (9, 1) | 0 | ⑨—⑦—⑤—③—① |
| (2, 3) | 0 | ②—③ |
| (2, 5) | 1 | ②—③—④—⑤ |
| (9, 5) | 0 | ⑨—⑦—⑤ |
| (7, 2) | 1 | ⑦—⑤—③—② |
| (8, 9) | 1 | ⑧—⑥—⑦—⑨ |
由图 2和表 2可知,所得运行线路配置及路径分配部分结果符合交通网络连通性、路径可达性和途中无缝换乘要求,满足了约束条件,能够完成OD对运输任务,且运行线在路网上的分布较均衡。因此认为模型的可行性在初始解中得到初步验证。
3.2 灵敏度分析为了从运行线路长度限制和目标函数权重角度对模型进行性能测试,探究二者变化对运行线路长度, 换剩次数的影响。进行灵敏度分析,分析改变运行线路长度限制大小、运营成本权重和乘客的广义旅行成本权重相对大小、换乘次数和路径长度权重相对大小后的运行线路设计和乘客路径分配结果变化。
3.2.1 运行线路长度限制影响为探究运行线路长度限制对运行线路选择、路径选择和换乘次数的影响,本研究确保道路容量、出行需求等其他条件不变,依次改变模型约束条件中最小运行线路长度和最大运行线路长度,得到的变化如表 3所示。
| 线路长度L限制/km | 线路长度/km | 线路数目/条 | 目标函数值 | 运行线路总长度/km | 换乘总次数/次 |
| 4≥L≥1 | 1 | 1 | 215.16 | 32 | 5 |
| 2 | 2 | ||||
| 3 | 5 | ||||
| 4 | 3 | ||||
| 4≥L≥2 | 2 | 2 | 215.16 | 32 | 5 |
| 3 | 4 | ||||
| 4 | 4 | ||||
| 4≥L≥3 | 3 | 6 | 219.12 | 34 | 5 |
| 4 | 4 | ||||
| 4≥L≥4 | 4 | 9 | 224.74 | 36 | 7 |
| 3≥L≥2 | 2 | 3 | 223.74 | 33 | 8(其中1条路径换乘2次) |
| 3 | 9 | ||||
| 5≥L≥2 | 3 | 2 | 208.56 | 32 | 3 |
| 4 | 4 | ||||
| 5 | 2 |
由表 3可知,在运行线路种类方面,种类随长度限制范围的变化而变化。例如,当长度范围为[1, 4]时,运行线路集合中出现了长度为1 km的运行线;当长度范围为[5, 2]时,运行线路集合中出现了长度为5 km的运行线,这与预期相符。目标函数值方面,随着运行线路长度可选范围扩大,运行线路的可选择范围也扩大,目标优化程度加深。运行线路总长度和换乘总次数方面,二者随运行线路长度可选范围的缩小而增大,且总换乘次数在运行线路长度限制为[3, 2]时达到峰值,出现一条路径需要换乘2次的情况。这说明运行线路可选择范围的扩大有利于降低运营成本和广义旅行成本。
3.2.2 目标函数权重影响本研究模型为双目标模型,双目标在目标函数中按照3部分表达,其中运行线路总长度代表运营成本,总换乘次数和路径总长度代表广义旅行成本。在模型中,将上述3部分分别赋予α,β,γ权重因子,α+β+γ=1。为削弱出行需求对双目标倾向性的影响,将出行需求值由5调整为1。道路容量值为4,运行线路长度限制为[3, 2],一条路径的换乘最大次数为2次。
(1) 运营成本和广义旅行成本对比分析
代表运营成本的运行线路总长度对应权重因子α,代表广义旅行成本的换乘总次数、路径总长度分别对应权重因子β和γ。改变2部分权重(α=0.8,β=γ=0.1和α=0.2,β=γ=0.4)获得差异性结果。当权重为α=0.8,β=γ=0.1时,运行线路总长度为30 km,换乘总次数为11次(其中,(1, 8)OD对和(2, 9)OD对需要换乘2次),路径总长度为85 km;当权重为α=0.2,β=γ=0.4时,运行线路总长度为35 km,换乘总次数为6次,其中,需要换乘的OD对均换乘1次,路径总长度为82 km。
对比权重为α=0.8,β=γ=0.1和α=0.2,β=γ=0.4获得的运行线路总长度、换乘总次数和路径总长度结果可得,α因子减小导致运行线路总长度减小,换乘总次数增大幅度明显,路径总长度也同时增大。这说明α因子较大时,目标优化倾向于通过增加换乘和路径绕行以减小运行线总长度,进而降低运营成本;反之,目标优化倾向于尽量减少换乘次数、选择较短路径、实现直达,进而降低广义旅行成本。该结果与预期相符。
(2) 换乘次数和路径长度对比分析
在保证目标倾向于降低广义旅行成本、固定运营成本权重因子的前提下,分别侧重路径选择和换乘次数设置了2组权重(α=0.1,β=0.1,γ=0.8和α=0.1,β=0.8,γ=0.1),选择(2,9)OD对(最短路径为②—③—⑤—⑦—⑨)的2组路径分配结果为例进行比较。当权重为α=0.1,β=0.1,γ=0.8时,选择路径②—③—⑤—⑦—⑨,换乘2次;当权重为α=0.1,β=0.8,γ=0.1时,选择路径②—③—④—⑥—⑦—⑨,换乘1次。
对比2组路径分配结果发现,更注重路径长度时,(2,9)OD对选择最短路径,通过2次换乘完成运输任务;更注重换乘次数时,(2,9)OD对选择较长路径,较前者减少一次换乘即完成运输任务,如图 3所示。路径分配结果共同展现了广义旅行成本2个因素的重要性倾向如何影响运行线路设计和乘客路径分配结果,验证了模型可行性。
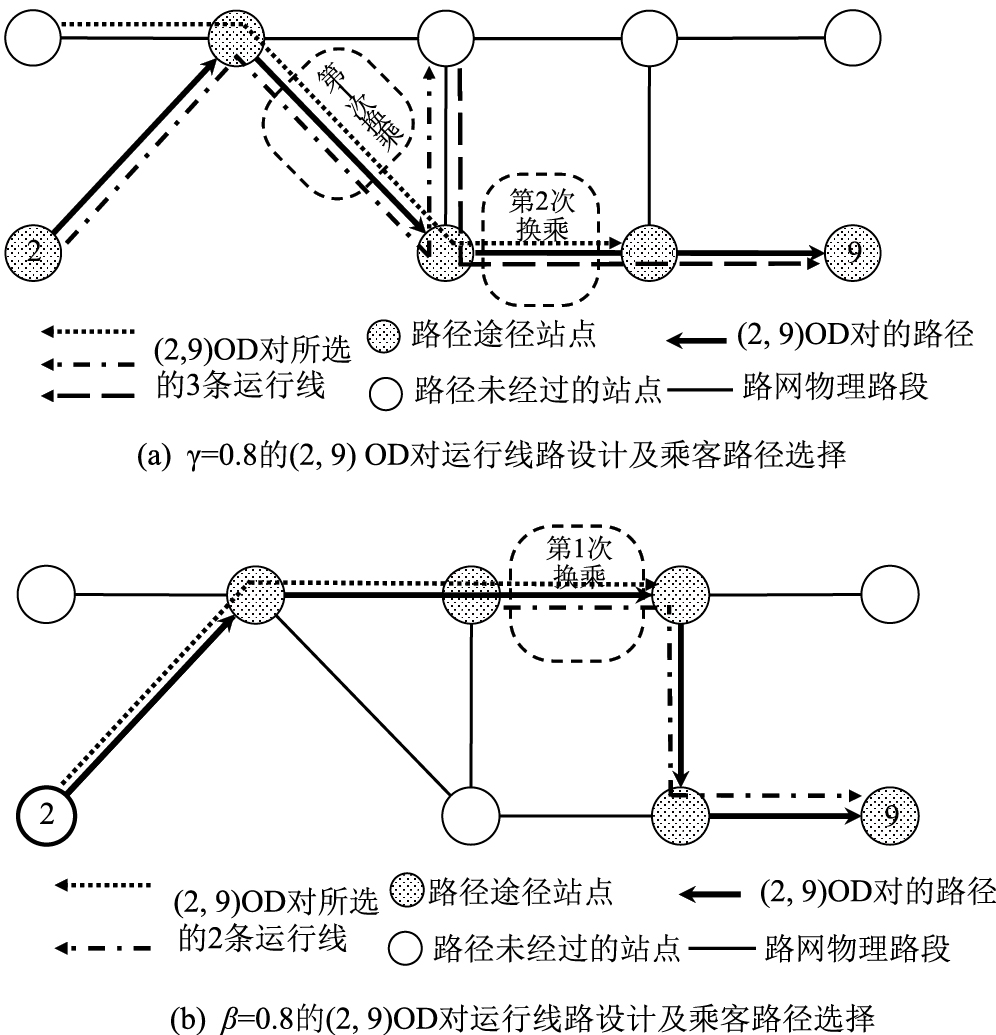
|
| 图 3 运行线路设计及乘客路径选择 Fig. 3 Operating line design and passenger path selection |
| |
4 结论
模块化公交的途中无缝换乘特性能够消除换乘等待时间,减小乘客的广义旅行成本。然而,当前针对模块化公交的研究鲜有思考运行线路设计优化,加之途中无缝换乘特性的实现对公交运行线路设计提出了乘客路径可达的新要求。因此,本研究从运行线路设计角度对模块化公交研究进行了补充。为了实现无缝换乘,围绕乘客路径可达的新要求提出了模块化公交的运行线路设计方法,从而构建了考虑乘客路径分配的模块化公交运行线路设计模型,在既定运行线路候选集、路径候选集和出行需求的条件下,获得了运行线路设计和与之相匹配的乘客路径分配结果。经算例检验,模型产生了合理的运行线路设计和路径分配结果。最后,改变算例运行线路长度限制和目标函数权重因子大小,对模型进行灵敏度分析,再次验证了模型可行性。
本研究对考虑乘客路径分配的模块化公交运行线路设计进行研究,模型所得结果达到了研究预期。然而,该方向尚有巨大研究空间与潜力,可考虑模块化公交的运行线路设计与时刻表协同优化、乘客路径分配方案适应动态需求变化,开发更高效算法以便后续将模型运用于实际大规模公交网络中。
| [1] |
KRUGMAN P. Geography and trade[M].
Cambridge, Massachusetts: The MIT Press, 1991.
|
| [2] |
崔旭川. 北京公共交通导向城市发展战略制定要点浅析[J]. 交通工程, 2021, 21(6): 63-67, 74. CUI Xuchuan. Analysis on the key points of public transport-oriented urban development in Beijing[J]. Journal of Transportation Engineering, 2021, 21(6): 63-67, 74. |
| [3] |
周锦强, 王海林, 杨雄, 等. 动态公交专用道分区控制方法设计及适用性分析[J]. 公路交通科技, 2024, 41(2): 166-172. ZHOU Jinqiang, WANG Hailin, YANG Xiong, et al. Design and applicability analysis on zoning control method for dynamic bus lane[J]. Journal of Highway and Transportation Research and Development, 2024, 41(2): 166-172. DOI:10.3969/j.issn.1002-0268.2024.02.017 |
| [4] |
中华人民共和国国务院新闻办公室. 中国交通的可持续发展[M]. 北京: 人民出版社, 2020. The State Council Information Office of the People 's Republic of China. Sustainable development of transport in China[M]. Beijing: People's Publishing House, 2020. |
| [5] |
CEDER A. Syncing sustainable urban mobility with public transit policy trends based on global data analysis [J/OL]. Scientific Reports, 2021: 14597(2021-07-20) [2023-10-01]. https://doi.org/10.1038/s41598-021-93741-4.
|
| [6] |
交通运输部. 2024年交通运输行业发展统计公报[R]. 北京: 交通运输部, 2025. Ministry of Transport of the People 's Republic of China. Statistical bulletin of transport industry development in 2024 [R]. Beijing: Ministry of Transport, 2025. |
| [7] |
胡立伟, 武加宝, 赵雪亭, 等. 常规公交运营脆弱性评价及发车优化研究[J]. 公路交通科技, 2024, 41(6): 173-181. HU Liwei, WU Jiabao, ZHAO Xueting, et al. Study on vulnerability evaluation of conventional bus operation and departure optimization[J]. Journal of Highway and Transportation Research and Development, 2024, 41(6): 173-181. DOI:10.3969/j.issn.1002-0268.2024.06.019 |
| [8] |
MAHMASSANI H S, SABERI M, ZOCKAIE A. Urban network gridlock: Theory, characteristics, and dynamics[J].
Procedia: Social and Behavioral Sciences, 2013, 80: 79-98.
DOI:10.1016/j.sbspro.2013.05.007 |
| [9] |
DAKIC I, YANG K D, MENENDEZ M, et al. On the design of an optimal flexible bus dispatching system with modular bus units: Using the three-dimensional macroscopic fundamental diagram[J].
Transportation Research Part B: Methodological, 2021, 148: 38-59.
DOI:10.1016/j.trb.2021.04.005 |
| [10] |
ZHANG Z H. TAFRESHIAN A, MASOUD N. Modular transit: Using autonomy and modularity to improve performance in public transportation [J/OL]. Transportation Research Part E: Logistics and Transportation Review, 2020.141: 102033. https://doi.org/10.1016/j.tre.2020.102033.
|
| [11] |
TIAN Q Y, LIN Y H, WANG D Z W, et al. Planning for modular-vehicle transit service system: Model formulation and solution methods [J/OL]. Transportation Research Part C: Emerging Technologies, 2022, 138: 103627. https://doi.org/10.1016/j.trc.2022.103627.
|
| [12] |
管德永, 吴晓芳, 赵杰, 等. 需求响应型公交车辆调度及路径优化[J]. 公路交通科技, 2022, 39(5): 140-148. GUAN Deyong, WU Xiaofang, ZHAO Jie, et al. Dispatch and route optimization of demand-responsive bus[J]. Journal of Highway and Transportation Research and Development, 2022, 39(5): 140-148. DOI:10.3969/j.issn.1002-0268.2022.05.017 |
| [13] |
何民, 李沐轩, 税文兵, 等. 可靠性和舒适性对响应式定制公交线路设计的影响[J]. 公路交通科技, 2019, 36(5): 145-151. HE Min, LI Muxuan, SHUI Wenbing, et al. Influence of reliability and comfort on responsive custom bus route design[J]. Journal of Highway and Transportation Research and Development, 2019, 36(5): 145-151. DOI:10.3969/j.issn.1002-0268.2019.05.020 |
| [14] |
吴红波, 郭敏, 杨肖肖. 基于地图API和GIS路径分析的城市公交车路网优化[J]. 北京交通大学学报, 2022, 46(1): 69-78. WU Hongbo, GUO Min, YANG Xiaoxiao. Optimization of urban bus network based on map API data and GIS path analysis[J]. Journal of Beijing Jiaotong University, 2022, 46(1): 69-78. |
| [15] |
姚佼, 邵楚薇, 鲍雨婕, 等. 基于双层规划模型的应急救援调度与路径选择集成优化[J]. 公路交通科技, 2021, 38(6): 149-158. YAO Jiao, SHAO Chuwei, BAO Yujie, et al. Bi-level programming model based integrated optimization of emergency rescue scheduling and route selection[J]. Journal of Highway and Transportation Research and Development, 2021, 38(6): 149-158. DOI:10.3969/j.issn.1002-0268.2021.06.019 |
| [16] |
奇格奇, 邹恺杰, 邹婕, 等. 面向异质化需求的无人驾驶电动公交接驳路径优化[J]. 清华大学学报(自然科学版), 2022, 62(7): 1178-1185. QI Geqi, ZOU Kaijie, ZOU Jie, et al. Feeder transit routing optimization of driverless electric buses for heterogeneous demands[J]. Journal of Tsinghua University (Science and Technology), 2022, 62(7): 1178-1185. |
| [17] |
GUAN J F, YANG H, WIRASINGHE S C. Simultaneous optimization of transit line configuration and passenger line assignment[J].
Transportation Research Part B: Methodological, 2006, 40(10): 885-902.
|
| [18] |
ZHOU Y, YANG H, WANG Y, et al. Integrated line configuration and frequency determination with passenger path assignment in urban rail transit networks[J].
Transportation Research Part B: Methodological, 2021, 145: 134-151.
|
 2025, Vol. 42
2025, Vol. 42



 ,
,