扩展功能
文章信息
- 桂水荣, 蓝天飞, 何锐.
- GUI Shuirong, LAN Tianfei, HE Rui
- 考虑车辆异质性的单车道入口匝道系统交通流仿真
- Traffic flow simulation on single lane on-ramp systems considering vehicle heterogeneity
- 公路交通科技, 2025, 42(8): 18-26
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(8): 18-26
- 10.3969/j.issn.1002-0268.2025.08.002
-
文章历史
- 收稿日期: 2023-07-28
2. 华东交通大学 土木建筑学院, 江西 南昌 330013;
3. 江西省赣南公路勘察设计院有限公司, 江西 赣州 341000
2. School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang, Jiangxi 330013, China;
3. Jiangxi Province Gannan Highway Survey and Design Institute Co., Ltd., Ganzhou, Jiangxi 341000, China
公路交通网络存在交通瓶颈路段,如进出匝道、收费站、道路维修路段等。大型车辆、车队也会对公路交通的运行产生明显影响,研究瓶颈路段交通流特征有助于了解交通堵塞传播机理,实现对交通流的有效控制。国内外研究人员运用多种理论模型深入探讨这类复杂瓶颈路段交通流。Cantisani[1]运用微观模型研究了道路设计、交通条件和驾驶行为对合流速度和合流位置的影响。Long[2]采用元胞传输模型揭示了交通堵塞的发生及其传播特征。郭海兵[3]利用全速差模型,揭示了合流区常发性瓶颈路段交通拥堵产生及消散机理。
元胞自动机模型能较好地模拟车辆运行状态且能够体现驾驶员驾驶行为特点,交通领域研究人员使用元胞自动机模型来研究瓶颈路段的交通流特征。入口匝道系统为典型的交通瓶颈,入口匝道交通流须与主干道交通流汇合才能通过交通瓶颈路段。在此期间,车辆存在大量变速与换道行为,交通动力学非常复杂。吴文静[4]运用元胞自动机建立了网联环境下合流区可变限速协调控制模型,车流密度较小时控制效果不明显,车流密度适中时控制效果显著,而车流密度较大时控制策略失效。王百里[5]考虑驾驶员行为特性,在NaSch模型基础上引入动态换道概率模拟合流区交通流,该模型可较好反映合流区驾驶员行为特性。马新露[6]考虑驾驶员性格及心理因素,构建了城市多路合流区元胞自动机模型,研究不同形式变速车道对合流区影响。为探究瓶颈路段异质交通流演变规律,吴德华[7]建立了考虑安全距离的NaSch上匝道模型,自动驾驶车辆占比对快速路瓶颈路段交通流影响显著。为研究自适应巡航车辆对上匝道交通流影响,华雪冬[8]考虑自适应巡航车辆影响,建立了上匝道系统异质交通流元胞自动机模型,自适应巡航车辆的加入有效地改善上匝道系统的交通流运行情况。Zeng[9]建立了事故条件下匝道系统的元胞自动机模型,事故引起的拥堵在自由流状态下不会传播到上游,对同步流上游交通产生明显影响。Sun[10]建立了元胞自动机模型,探讨变道管理对匝道口交织区域运营效率影响,使用车道标记强迫驶出匝道的车辆提前换车道可以提高运营效率。邓超[11]考虑连续换道行为的危险性及预测需求,提取11维特征构建宽度学习模型。潘芋燕[12]为更精确估计过饱和状态通行时间,提出基于交通流基本图的新阻抗函数,为拥堵道路阻抗估计及交通规划提供了更可靠工具。
上述研究均集中于研究小型车辆或驾驶人员性格因素对合流区交通影响,然而,入口匝道系统的交通流常为异质交通流,即车辆类型(如小汽车、客车、各种类型货车、特种车)各异的交通流。重型车辆与小汽车的车辆动力性能(如车辆质量、悬架刚度、阻尼等)不同,行驶过程的操作性能(车辆行驶加、减速度,车辆换道安全距离等)要求不同,具有相对较大的质量和载荷,有惯性大、侧倾中心高、轴距长、加速能力差、制动距离长等特点,对周围交通影响明显。本研究依据重型车辆与小汽车的物理特性不同,司机对2种类型车辆安全距离判断也必不相同,建立双车道安全距离模型研究四车道高速公路入口匝道系统的异质交通流特性,分析合流区异质交通流作用时,重载货车占比、主路交通流及匝道交通流对合流区的影响。
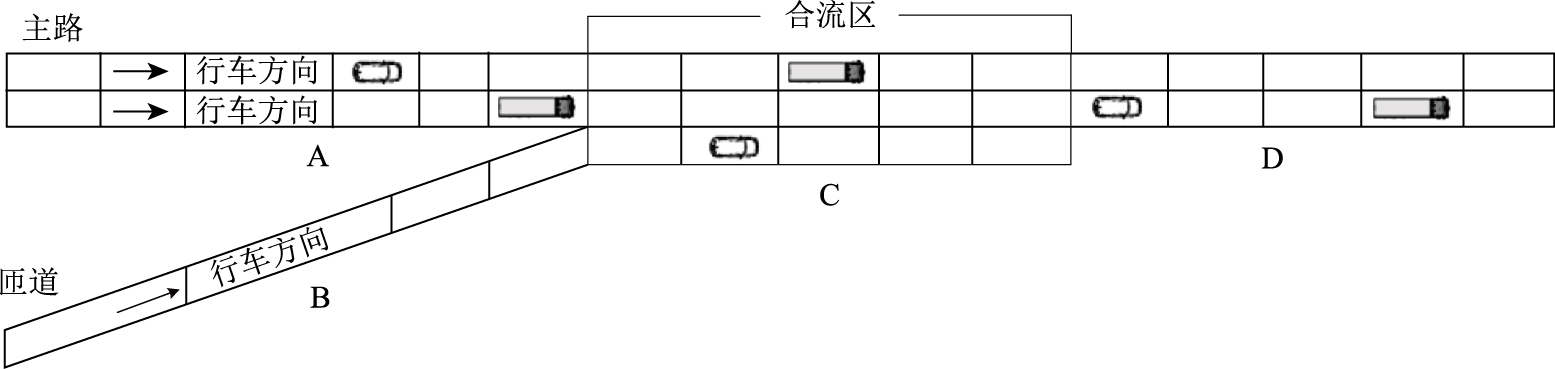
1 入口匝道系统异质交通流模型选取典型的双向四车道高速公路入口为研究对象,入口匝道系统平面布置如图 1所示。图中入口匝道系统分为4个部分:A(合流区上游主路),B(合流区上游匝道),C(合流区),D(合流区下游)。主路为双车道,匝道设计为单车道。匝道入口系统车辆分为2种:一种为主路直行车辆,从合流区上游主路2条车道驶入,从合流区下游驶出;另一种为匝道车辆,从匝道驶入,经过合流区换道驶入主路,最后从合流区下游驶出。
|
| 图 1 入口匝道系统示意图 Fig. 1 Schematic diagram of on-ramp system |
| |
1.1 跟弛规则模型 1.1.1 安全距离计算
双车道安全距离模型是基于单车道安全距离模型[13-15],考虑车辆间距、车辆性能及相邻车辆行驶速度建立起来的双车道元胞自动机模型。在该元胞自动机模型中,单车道划分为N个元胞,道路分为2×N个元胞。模型中,需考虑车辆行驶速度减速至0,每个时间段内两车距离变化。可根据式(1)~ (3)分别计算车辆的加速安全距离、保持当前速度的安全距离及减速安全距离[16]。加速安全距离dnacc (t)的联立表达式为:
| $ \left\{\begin{array}{l} \Delta t_{n, \text { acc }}=\left[v_{n}(t)+a_{n}\right] / a_{n}^{\mathrm{m}} \\ \Delta t_{n-1, \text { acc }}=\left[v_{n-1}(t)-a_{n-1}^{\mathrm{m}}\right] / a_{n-1}^{\mathrm{m}}=\Delta t_{n-1} \\ S_{n, \text { acc }}=\sum\limits_{i=0}^{\left[\Delta t_{n, \text { acc }}\right]}\left\{\left[v_{n}(t)+a_{n}\right]-i \cdot a_{n}^{\mathrm{m}}\right\} \\ S_{n-1, \text { acc }}=\sum\limits_{i=0}^{\left[\Delta t_{n-1}\right]}\left\{\left[v_{n-1}(t)-a_{n-1}^{\mathrm{m}}\right]-i \cdot a_{n-1}^{\mathrm{m}}\right\}=S_{n-1} \\ d_{n}^{\text {acc }}(t)=\max \left(0, S_{n, \text { acc }}-S_{n-1}\right) \end{array}\right., $ | (1) |
式中,vn-1 (t)、vn (t)分别为t时刻前车和后车的行驶速度;an-1和an分别为前车和后车的一般加速度;amn-1和amn分别为前车和后车的紧急制动加速度;[Δtn-1, acc]和[Δtn, acc]分别为前车以当前减速度制动至停止和后车从加速状态开始紧急制动至停止的时间步数(向下取整);Sn, acc和Sn-1, acc分别为前车和后车在制动时间内的累计行驶距离;i为遍历时间步的整数变量,用于累计多个微小时间间隔内的行驶距离。
同理可推测保持当前速度的安全距离dnkeep (t)和减速安全距dndec (t)为:
| $ \left\{\begin{array}{l} \Delta t_{n, \text { keep }}=v_{n}(t) / a_{n}^{\mathrm{m}} \\ \Delta t_{n-1, \text { keep }}=\left[v_{n-1}(t)-a_{n-1}^{\mathrm{m}}\right] / a_{n-1}^{\mathrm{m}}=\Delta t_{n-1} \\ S_{n, \text { keep }}=\sum\limits_{i=0}^{\left[\Delta t_{n, \text { keep }}\right]}\left[v_{n}(t)-i \cdot a_{n}^{\mathrm{m}}\right] \\ S_{n-1, \text { keep }}=\sum\limits_{i=0}^{\left[\Delta t_{n-1}\right]}\left\{\left[v_{n-1}(t)-a_{n-1}^{\mathrm{m}}\right]-i \cdot a_{n-1}^{\mathrm{m}}\right\}=S_{n-1} \\ d_{n}^{\text {keep }}(t)=\max \left(0, S_{n, \text { keep }}-S_{n-1}\right) \end{array}\right., $ | (2) |
| $ \left\{\begin{array}{l} \Delta t_{n, \mathrm{dec}}=\left[v_{n}(t)-a_{n}\right] / a_{n}^{\mathrm{m}} \\ \Delta t_{n-1, \mathrm{dec}}=\left[v_{n-1}(t)-a_{n-1}^{\mathrm{m}}\right] / a_{n-1}^{\mathrm{m}}=\Delta t_{n-1} \\ S_{n, \mathrm{dec}}=\sum\limits_{i=0}^{\left[\Delta t_{n, \mathrm{dec}}\right]}\left\{\left[v_{n}(t)-a_{n}\right]-i \cdot a_{n}^{\mathrm{m}}\right\} \\ S_{n-1, \mathrm{dec}}=\sum\limits_{i=0}^{\left[\Delta t_{n-1}\right]}\left\{\left[v_{n-1}(t)-a_{n-1}^{\mathrm{m}}\right]-i \cdot a_{n-1}^{\mathrm{m}}\right\}=S_{n-1} \\ d_{n}^{\mathrm{dec}}(t)=\max \left(0, S_{n, \mathrm{dec}}-S_{n-1}\right) \end{array}\right.。$ | (3) |
为了后序表述方便,定义函数f (x, y)如式(4)所示。
| $ \begin{gather*} f\left(x_{1}, y_{1} ; x_{2}, y_{2}\right)=\max \cdot \\ \left\{0, \left[\sum\limits_{i=0}^{\left[x_{1} / y_{1}\right]}\left(x_{1}-i \cdot y_{1}\right)-\sum\limits_{i=0}^{\left[x_{2} / y_{2}\right]}\left(x_{2}-i \cdot y_{2}\right)\right]\right\} 。\end{gather*} $ | (4) |
令
| $ d_{n}^{\mathrm{acc}}(t)=f\left[v_{n}(t)+a_{n}, a_{n}^{\mathrm{m}} ; v_{n-1}(t)-a_{n-1}^{\mathrm{m}}, a_{n-1}^{\mathrm{m}}\right] 。$ | (5) |
类比NaSch模型跟弛规则[17],从t至t+1时刻,根据车辆间距dn (t)与3个安全距离之间关系,基于安全距离的元胞自动机模型车辆行驶规律,按如下规则进行位置更新演化。
(1) 加速规则
t时刻,目标车辆与前车车距不小于加速安全距离,且车速小于最大速度vmax,目标车辆加速;目标车辆与前车车距小于加速安全距离,但不小于保持当前速度的安全距离,目标车辆保持当前速度。
| $ v_{n}(t+1)=\left\{\begin{array}{l} \min \left[v_{n}(t)+a_{n}, v_{\max }\right], \text { 若 } d_{n}(t) \geqslant d_{n}^{\mathrm{acc}}(t) \\ v_{n}(t), \quad \text { 若 } d_{n}^{\mathrm{keep}}(t) \leqslant d_{n}(t)<d_{n}^{\mathrm{acc}}(t) \end{array}\right. \text {, } $ | (6) |
式中dn (t)为目标车辆与前车车距。
(2) 减速规则
t时刻,目标车辆与前车车距小于当前速度的安全距离,但不小于减速安全距离时,目标车辆减速;目标车辆与前车车距小于减速安全距离,目标车辆紧急制动。
| $v_n(t+1)=\\ \left\{\begin{array}{l} \max \left[v_{n}(t)-a_{n}, 0\right], \text { 若 } d_{n}^{\mathrm{dec}}(t) \leqslant d_{n}(t)<d_{n}^{\mathrm{keep}}(t) \\ \max \left[v_{n}(t)-a_{n}^{\mathrm{m}}, 0\right], \text { 若 } d_{n}(t)<d_{n}^{\mathrm{dec}}(t) \end{array}\right. \text { 。} $ | (7) |
(3) 随机慢化
未经历减速的车辆,运行过程考虑进行随机慢化。若车辆历经减速再对其进行随机慢化,在同一个时间步内减速达2amn,这超过了车辆的机械性能,不符合实际。预先设定随机慢化概率R,rand随机生成介于0至1区间的慢化随机数Rd。若生成的随机数Rd<R,则车辆进行减速;若Rd>R,则车辆不进行此次随机慢化。
| $ \begin{gather*} v_{n}(t+1)=\max \left[v_{n}(t)-a_{n}, 0\right], \\ \text { 若 }\left\{\begin{array}{l} R_{\mathrm{d}}<R \\ d_{n}(t) \geqslant d_{n}^{\text {keep }}(t)^{\circ} \end{array}\right. \end{gather*} $ | (8) |
(4) 位置更新
t时刻完成循环,按式(9)更新位置。
| $ x_{n}(t+1)=x_{n}(t)+v_{n}(t+1) \cdot \Delta t_{\circ} $ | (9) |
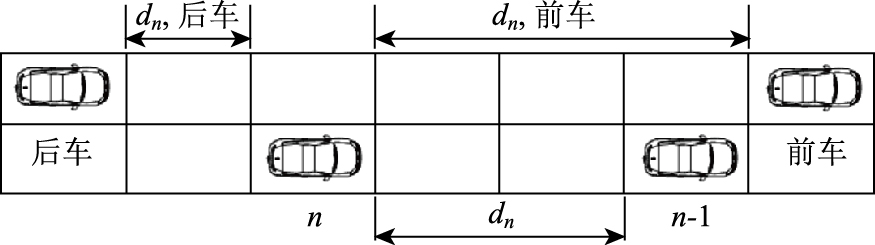
根据换道场景,换道规则分为主路换道规则与合流区匝道换道规则。主路车辆的换道规则可分为自由换道规则及强行换道规则。合流区换道规则可分为自由换道规则、强行换道规则及末端换道规则。自由换道指在不影响目标车道后车前提下,车辆进行换道行为;强行换道指车辆意识到前方有多辆车停止运动,选择强行换到交通情况更好的车道,这种换道行为可能造成目标车道后车减速。换道规则如图 2所示。
|
| 图 2 换道规则示意图 Fig. 2 Schematic diagram of lane-changing rules |
| |
1.2.1 主路换道规则 1.2.1.1 自由换道(1)自由换道动机
当目标车辆不能在当前车道以最大速度行驶,且无法加速行驶时,目标车道有足够安全距离进行加速,则产生自由换道动机为:
| $ \begin{gather*} d_{n}(t)<d_{n}^{\text {acc }}(t) \text { 且 } v_{n}(t)<v_{\text {max }}(t) \text { 且 } \\ d_{n, \text { front }}(t) \geqslant d_{n, \text { front }}^{\text {acc }}(t), \end{gather*} $ | (10) |
式中dn, frontacc (t)为车辆在目标车道上加速行驶的安全距离。
| $ \begin{align*} & d_{n, \text { front }}^{\text {acc }}(t)=f\left[v_{n}(t)+a_{n}, a_{n}^{\mathrm{m}}\right. \\ & \left.v_{n, \text { front }}(t)-a_{n, \text { front }}^{\mathrm{m}}, a_{n, \text { front }}^{\mathrm{m}}\right] 。\end{align*} $ | (11) |
(2) 自由换道安全条件
自由换道不会对目标车道后车产生影响:
| $ \begin{equation*} d_{n, \text { back }}(t) \geqslant d_{n, \text { back }}^{\text {keep }}(t), \end{equation*} $ | (12) |
式中dn, backkeep(t)为目标车道后车保持当前速度行驶的安全距离。
| $ d_{n, \text { back }}^{\text {keep }}(t)=f\left[v_{n, \text { back }}(t), a_{n, \text { back }}^{\mathrm{m}} ; v_{n}(t)-a_{n}^{\mathrm{m}}, a_{n}^{\mathrm{m}}\right] \text { 。} $ | (13) |
(1) 强行换道动机
当目标车辆在本车道上减速至0不能前行,且前方一辆车均处于静止状态,而目标车道有足够的距离进行加速运动,此时产生强行换道动机:
| $ \begin{gather*} d_{n}(t)<d_{n}^{\text {acc }}(t), v_{n}(t)=v_{n-1}(t)=0 \text { 且 } \\ d_{n, \text { front }}(t) \geqslant d_{n, \text { front }}^{\text {acc }}(t) 。\end{gather*} $ | (14) |
(2) 强行换道安全条件
强行换道可能使目标车道后车减速,但不会使其进行紧急制动至停止。
| $ \begin{equation*} d_{n, \text { back }}(t) \geqslant d_{n, \text { back }}^{\text {dec }}(t), \end{equation*} $ | (15) |
式中dn, backdec (t)为目标车道后车减速行驶的安全距离。
| $ \begin{align*} d_{n, \text { back }}^{\text {dec }}(t)= & f\left[v_{n, \text { back }}(t)-a_{n, \text { back }}, a_{n, \text { back }}^{\mathrm{m}} ;\right. \\ & \left.v_{n}(t)-a_{n}^{\mathrm{m}}, a_{n}^{\mathrm{m}}\right] 。\end{align*} $ | (16) |
当合流区匝道车辆不能在当前车道以最大速度行驶,且无法加速行驶,因合流区匝道车辆需进入合流区,当目标车道有足够安全距离保持当前速度行驶时,则产生自由换道动机:
| $ \begin{gather*} d_{n}(t)<d_{n}^{\text {acc }}(t), v_{n}(t)<v_{\max }(t) \text { 且, } \\ d_{n, \text { front }}(t) \geqslant d_{n, \text { front }}^{\text {keep }}(t) \end{gather*} $ | (17) |
式中dn, frontkeep (t)为车辆在目标车道上保持当前速度行驶的安全距离。
| $ d_{n, \text { front }}^{\text {keep }}(t)=f\left[v_{n}(t), a_{n}^{\mathrm{m}} ; v_{n, \text { front }}(t)-a_{n, \text { front }}^{\mathrm{m}}, a_{n, \text { front }}^{\mathrm{m}}\right] \circ $ | (18) |
(2) 自由换道安全条件
| $ d_{n, \text { back }}(t) \geqslant d_{n, \text { back }}^{\text {keep }}(t), $ | (19) |
| $ d_{n, \text { back }}^{\text {keep }}(t)=f\left[v_{n, \text { back }}(t), a_{n, \text { back }}^{\mathrm{m}} ; v_{n}(t)-a_{n}^{\mathrm{m}}, a_{n}^{\mathrm{m}}\right] 。$ | (20) |
当匝道车辆在本车道上减速至0不能前行,而目标车道有足够的距离进行加速运动,此时产生强行换道动机:
| $ d_{n}(t)<d_{n}^{\text {acc }}(t), v_{n}(t)=0 \text { 且 } d_{n, \text { front }}(t) \geqslant d_{n, \text { front }}^{\text {acc }}(t) \text { 。} $ | (21) |
(2) 强行换道的安全条件
强行换道可能使目标车道后车减速,但不会使其进行紧急制动至停止:
| $ d_{n, \text { back }}(t) \geqslant d_{n, \text { back }}^{\mathrm{dec}}(t), $ | (22) |
| $ d_{n, \text { back }}^{\mathrm{dec}}(t)=f\left[v_{n, \text { back }}(t)-a_{n, \text { back }}, a_{n, \text { back }}^{\mathrm{m}} \right. 。\\ \;\;\;\;\;\;\;\;\;\;\;\;\left.v_{n}(t)-a_{n}^{\mathrm{m}}, a_{n}^{\mathrm{m}}\right] $ | (23) |
入口匝道交通模型采用开口边界条件,假设每条车道的入口区域长度为lmc,在每个时间步对模型更新时,均有概率在合流区上游入口处产生车辆驶入入口匝道系统,此概率为进车概率。当道路上的车辆更新完成后,在下一个时间步,如果车道入口区域未被任何车辆占用,则一辆速度为ve的车辆将以概率α进入。当该车辆进入车道时,以概率k设置重载货车。随机产生的每辆新生成车辆的速度ve须对应可能的最大行驶速度,以便新生成车辆与最后一辆车的距离等于保持当前速度的安全距离dkeep,则新生成车辆的位置为min(xlast-llast-lmc, lmc)。其中xlast和llast表示车道上尾车的位置和长度。合流区下游处,若头车位置大于道路长度,则道路尽头的头车以概率β驶出路段,紧跟其后的第2辆车成为新的头车。
2 系统仿真分析基于入口匝道系统异质交通流模型,运用Matlab程序语言,编写开放边界条件下的平行式合流仿真程序,研究重载货车占比、主路交通流及匝道交通流对合流区交通流的影响。
2.1 参数设置本研究基于入口匝道系统的交通运行特点,依据《公路路线设计规范》(JTG D20—2017),参考Yang[18],Feng[19],Li[14]的研究成果,设置模型仿真参数。
(1) 元胞参数:每个元胞长度为0.5 m,合流区上游共3条车道,每条车道元胞数为1 000个;合流区共3条车道,每条车道元胞数为460个;合流区下游共2条车道,每条车道元胞数为1 000个。其中小汽车长度为15个元胞,重载货车长度为30个元胞;小汽车最大速度为67个元胞(约为120 km/h),重载货车最大速度为45个元胞(约为81 km/h);小汽车加速度为5个元胞(2.5 m/s2),重载货车加速度为3个元胞(1.5 m/s2);小汽车一般减速度为5个元胞(2.5 m/s2),重载货车一般减速度为3个元胞(1.5 m/s2);小汽车紧急制动减速度为8个元胞(4 m/s2),重载货车紧急制动减速度为5个元胞(2.5 m/s2);小汽车随机慢化概率取0.2,重载货车随机慢化概率取0.1,道路尽头的头车以概率1驶出路段。
(2) 道路参数:高速公路双车道设计速度为120 km/h,主路最大服务交通量为1 650 pcu/ (h·ln),其中pcu为标准车当量数,h为小时,ln为车道数量。
(3) 仿真参数:每次仿真运行13 600个时间步,选取最后3 600个时间步的车辆数据进行分析。为消除随机性影响,每种情况运行10次,取10次数据平均值。
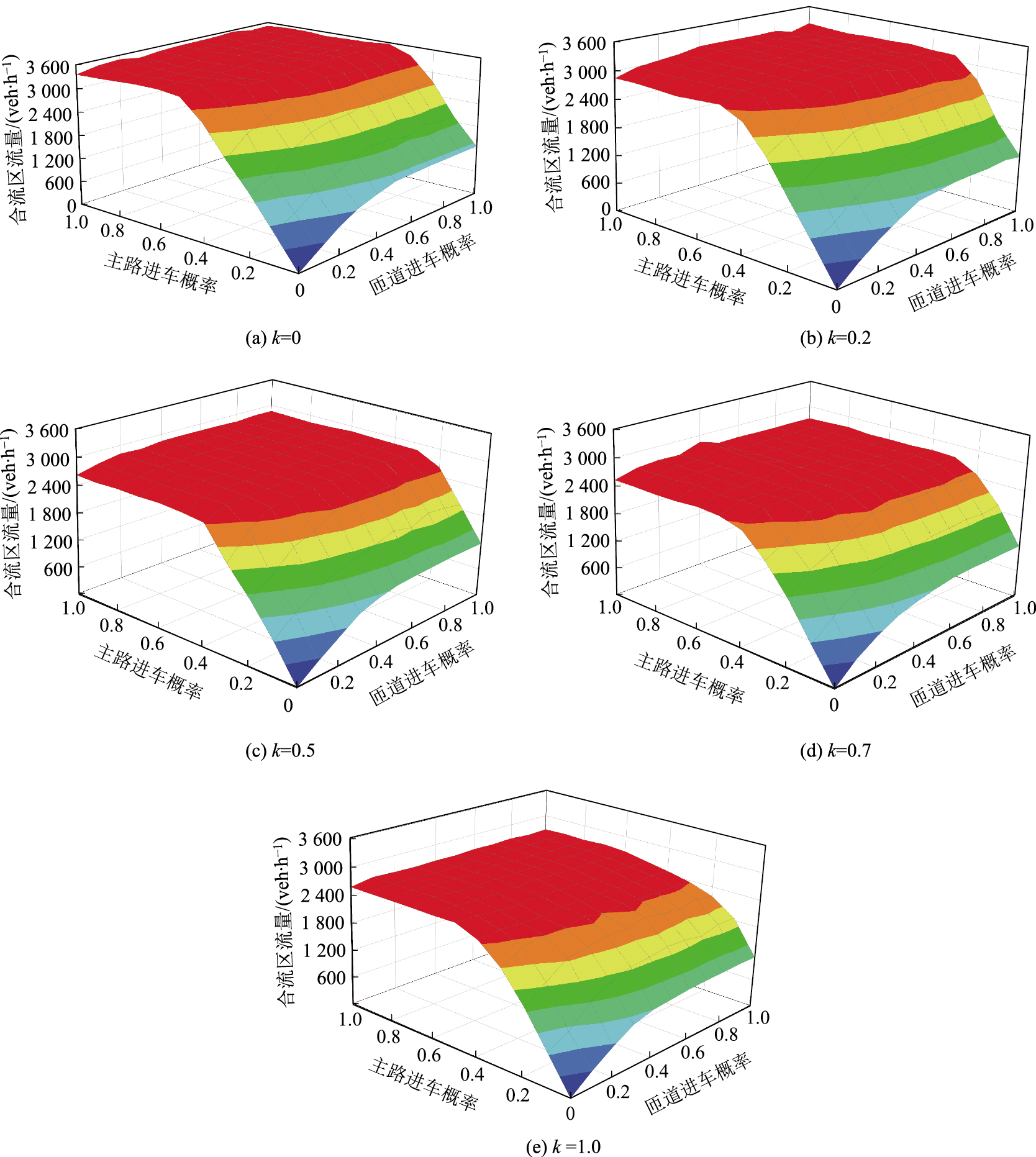
2.2 重载货车比例对合流区影响为研究重载货车占比对合流区车流的影响,设进入入口匝道系统的重载货车概率k[15]为0, 0.2, 0.5, 0.7, 1.0。合流区饱和流量是指单位时间内车辆通过合流区交叉口的最大流量,即排队车辆加速到正常行驶速度时,单位时间内通过合流区交叉口的稳定车流量。重载货车不同占比场景下合流区流量如图 3所示。由图可见,随着重载货车占比增大,合流区饱和流量逐渐减少。这是因为,重载货车占用道路空间较大,车辆行驶灵活性低,重载货车恶化合流区性能。当主路进车概率及匝道进车概率均很小时,合流区流量随着进车概率增大而线性增加,此时主路与匝道的交通流均为自由流。当匝道进车概率为0时,饱和车流量随着重载货车比例增大而减小。当主路进车概率为0时,饱和车流量并没有随着重载货车比例增大而发生明显变化。主路进车概率为0时,合流区主路车辆与合流区匝道车辆之间没有相互作用,饱和车流量的大小完全取决于匝道车流。因模型入口匝道车道数为1,匝道车辆不能通过变道超越前方重载货车。因此,车流量及车速大小完全取决于重载货车性能。
|
| 图 3 不同比例重载货车场景下的合流区流量 Fig. 3 Merging area traffic flow with different proportions of heavy-duty trucks |
| |
2.3 主路交通流对合流区影响
令进入匝道的重载货车概率为0.1,匝道进车概率为0.2,将进入主路车辆为重载货车概率km分别设置为0, 0.2, 0.5, 0.7, 1.0,研究主路交通流变化对合流区交通流的影响。
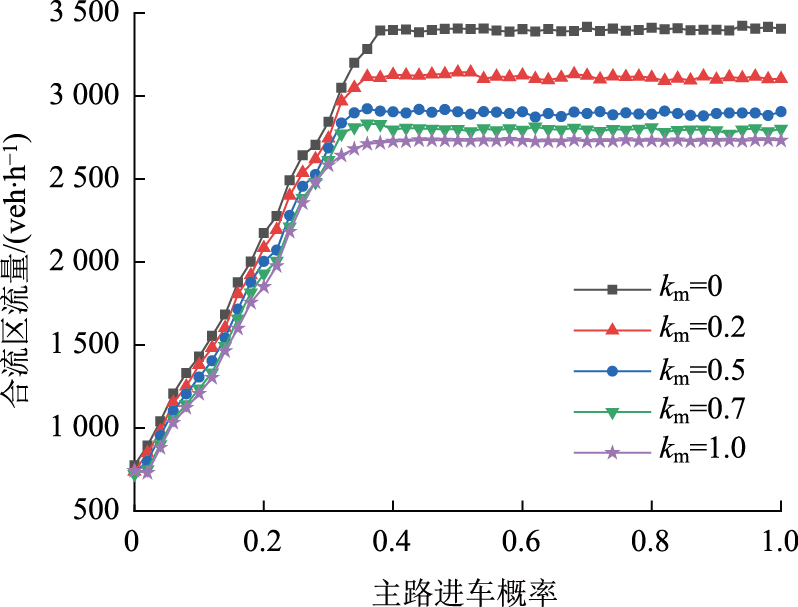
2.3.1 主路交通流对合流区流量影响主路不同的进车概率及重载货车比例下,主路交通流与合流区流量关系如图 4所示。由图可见,车流中仅有小汽车时合流区饱和流量最大,其中最大流量约为3 490 veh/h,而主路车流全为重载货车时合流区饱和流量最小,最大流量约为2 808 veh/h。当主路进车概率小于0.4时,合流区车流为自由流状态,合流区流量随进车概率的增大而增大;当主路进车概率到达临界时,合流区流量达到饱和状态,合流区流量不再随主路进车概率的增大而发生显著变化。主路进车概率临界值随主路重载货车比例的增大而减小,饱和流量随着主路重载货车比例的增大而减少。这是因为重载货车在驾驶过程中更为谨慎,跟车过程中需要更大的安全距离。与同步流相比,饱和流状态下重载货车比例对交通流的影响更为显著。同步流的重载货车速度与小汽车速度相差不大,重载货车瓶颈效应减弱,而在饱和流时,会出现走走停停现象,重载货车加速性能较差,从而影响整个交通流。随着主路重载货车比例的增加,合流区饱和流量之间的差值越来越小,主路重载货车比例对合流区饱和流量的影响越来越小。
|
| 图 4 主路交通流与合流区流量关系 Fig. 4 Relation between main road traffic flow and merging area traffic flow |
| |
2.3.2 主路交通流对合流区速度影响
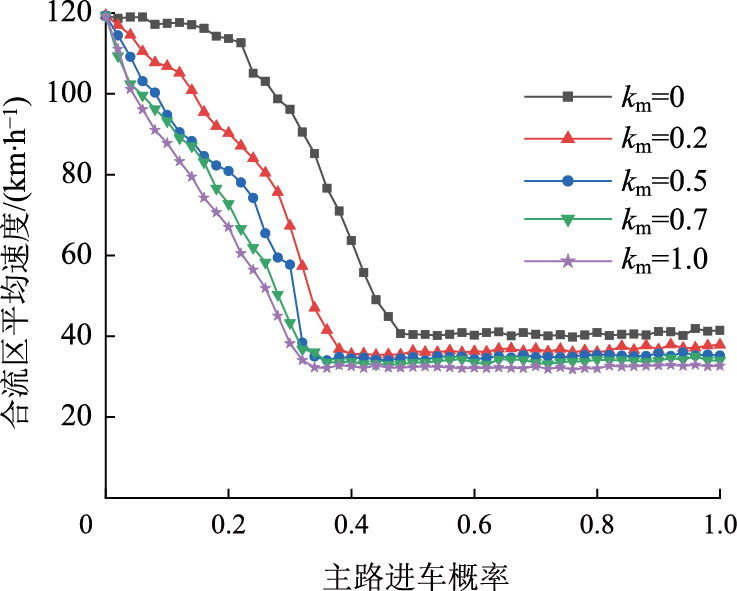
主路不同进车概率及重载货车占比作用下,主路交通流与合流区平均速度关系如图 5所示。由图可见,当主路进车概率较小且车流全为小汽车时,合流区车辆平均速度变化不大且均能以最高速度行驶。这说明主路进车概率对合流区车流影响不大,车辆在合流区可以畅通行驶。当主路车流有重载货车且主路进车概率较小时,合流区车辆平均速度随着主路进车概率的增大而逐渐减小。这说明主路进车概率较低时,重载货车的最大速度略低于小汽车的最大速度,主路重载货车的参与影响了合流区车辆的平均速度。当主路进车概率较大时,合流区车辆平均速度随着主路进车概率的增大基本保持不变,这时主路进车概率对车流影响不大。当主路进车概率大于0且小于0.4时,重载货车的加入对合流区车辆速度产生了明显影响。当主路进车概率大于0.5时,保持相同进车概率、不同重载货车比例对合流区车速影响不大,当主路进车概率较大时,主路重载货车占比对合流区车辆速度影响较小。
|
| 图 5 主路交通流与合流区平均速度关系 Fig. 5 Relation between main road traffic flow and merging area average speed |
| |
2.4 匝道交通流对合流区影响
令进入主路重载货车概率为0.1,主路进车概率为0.2时,将进入匝道的重载货车概率kr设置为0, 0.2, 0.5, 0.7, 1.0,研究匝道交通流变化对合流区交通流的影响。
2.4.1 匝道交通流对合流区流量影响匝道不同进车概率及重载货车占比作用下,匝道交通流与合流区流量关系如图 6所示。由图可见,车流中仅有小汽车时合流区饱和流量最大,其中最大流量约为3 160 veh/h,而匝道车流全为重载货车时合流区饱和流量最小,其中最大流量约为2 752 veh/h。当匝道进车概率较小时,合流区车流为自由流状态,合流区流量随着匝道进车概率的增大而增大;当匝道进车概率较大时,主路车流受匝道车流的干扰,合流区车流量增速减缓;当匝道进车概率继续增大时,合流区流量不再发生明显变化。当匝道进车概率小于0.3时,匝道重载货车的加入对合流区交通流影响较小。当匝道进车概率大于0.5时,合流区车流量为饱和流,匝道重载货车比例的增大对合流区饱和流量影响越来越小,此时匝道重载货车比例超过0.5,匝道重载货车比例的增大对合流区流量影响很小。

|
| 图 6 匝道交通流与合流区流量关系 Fig. 6 Relation between on-ramp traffic flow and merging area traffic flow |
| |
2.4.2 匝道交通流对合流区速度影响
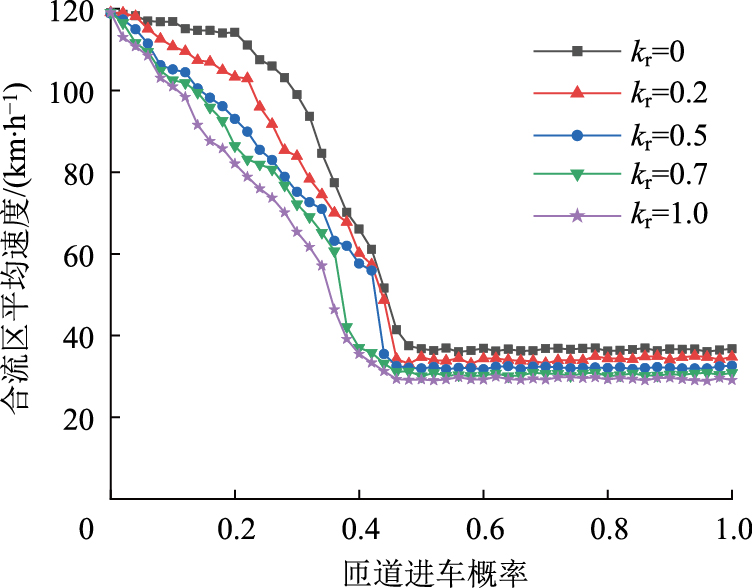
匝道不同进车概率及重载货车占比作用下,匝道交通流与合流区平均速度关系如图 7所示。如图可见,当匝道进车概率较小且车流全为小汽车时,合流区车辆平均速度变化较小且均能以最高速度行驶。此时匝道进车概率对合流区车流影响不大,车辆在合流区可以畅通行驶。当匝道车流有重载货车且匝道进车概率较小时,合流区车辆平均速度随着匝道进车概率的增大而逐渐减小。当匝道进车概率较大时,合流区车辆平均速度随着匝道进车概率的增大基本保持不变,此时匝道进车概率对车流影响不大。当匝道进车概率大于0且小于0.3时,重载货车的加入对合流区车辆速度产生了明显影响。值得注意的是,当匝道进车概率约为0.3时,只要匝道上有重载货车,合流区速度均发生了较大的变化。当匝道进车概率大于0.5,且匝道进车概率相同时,匝道不同重载货车比例对合流区车速的影响不大。
|
| 图 7 匝道交通流与合流区速度关系 Fig. 7 Relation between on-ramp traffic flow and merging area speed |
| |
3 结论
本研究基于双车道安全距离元胞自动机模型,考虑入口匝道系统异质交通流特性,研究异质交通流作用下,重载货车占比、主路交通流及匝道交通流对合流区的影响。
(1) 合流区饱和流量随着重载货车比例增大而逐渐减小。主路进车概率小于0.4,匝道进车概率小于0.3时,合流区交通流为自由流状态,重载货车比例变化对合流区交通流影响较小。
(2) 当主路进车概率小于0.4时,合流区流量随主路进车概率增大而线性增加,合流区速度随主路进车概率增大而减小;主路进车概率超过临界值时,合流区饱和流量随主路重载货车比例的增大而减小。
(3) 当匝道进车概率小于0.3时,合流区流量随着匝道进车概率增大而线性增加,合流区速度随匝道进车概率增大而减小,匝道重载货车比例对速度有较大影响;当匝道进车概率大于0.5时,合流区流量达到饱和,合流区饱和流量随着匝道重载货车比例增大而减小。
(4) 入口匝道异质交通流的交通堵塞传播机理能有效缓解入口匝道合流区交通拥堵,为科学管理入口匝道交通流提供理论依据。
| [1] |
CANTISANI G, DEL S G, DI B G. Calibration and validation of and results from a micro-simulation model to explore drivers ' actual use of acceleration lanes[J].
Simulation Modelling Practice and Theory, 2018, 89: 82-99.
DOI:10.1016/j.simpat.2018.09.007 |
| [2] |
LONG K J, LIN Q, GU J, et al. Exploring traffic congestion on urban expressways considering drivers ' reasonable behavior at merge/diverge sections in China[J/OL]. Sustainability, 2018, 10(12): 4359. (2018-11-22) [2023-07-01]. https://doi.org/10.3390/su10124359.
|
| [3] |
郭海兵, 曲大义, 洪家乐, 等. 基于全速度差模型的城市快速路合流区交通流特性研究[J]. 青岛理工大学学报, 2021, 42(4): 100-107. GUO Haibing, QU Dayi, HONG Jiale, et al. Study on traffic characteristics of expressway confluence area based on full velocity difference model[J]. Journal of Qingdao University of Technology, 2021, 42(4): 100-107. |
| [4] |
吴文静, 战勇斌, 杨丽丽, 等. 考虑安全间距的合流区可变限速协调控制方法[J]. 吉林大学学报(工学版), 2022, 52(6): 1315-1323. WU Wenjing, ZHAN Yongbin, YANG Lili, et al. Coordinated control method of variable speed limit in on-ramp area considering safety distance[J]. Journal of Jilin University (Engineering and Technology Edition), 2022, 52(6): 1315-1323. |
| [5] |
王百里, 杨晓芳, 刘红杏. 道路交通合流区换道行为仿真研究[J]. 计算机仿真, 2016, 33(2): 211-215, 238. WANG Baili, YANG Xiaofang, LIU Hongxing. Lane-changing behavior simulation research in traffic merging area[J]. Computer Simulation, 2016, 33(2): 211-215, 238. |
| [6] |
马新露, 王迪, 胡月豪, 等. 变速车道影响下的城市道路多路合流区域换道交通流特性研究[J]. 重庆交通大学学报(自然科学版), 2018, 37(3): 76-87. MA Xinlu, WANG Di, HU Yuehao, et al. Lane-changing traffic flow characteristics of the urban multi-road merging region affected by speed change ramp[J]. Journal of Chongqing Jiaotong University, 2018, 37(3): 76-87. |
| [7] |
吴德华, 陈家伟, 彭锐, 等. 快速路上匝道瓶颈路段异质交通流演变规律[J]. 贵州大学学报(自然科学版), 2020, 37(4): 99-104. WU Dehua, CHEN Jiawei, PENG Rui, et al. Heterogeneous traffic flow evolution rule in expressway on-ramp bottleneck section[J]. Journal of Guizhou University (Natural Sciences), 2020, 37(4): 99-104. |
| [8] |
华雪东, 王炜, 王昊. 考虑自适应巡航车辆影响的上匝道系统混合交通流模型[J]. 物理学报, 2016, 65(8): 219-231. HUA Xuedong, WANG Wei, WANG Hao. A hybrid traffic flow model with considering the influence of adaptive cruise control vehicles and on-ramps[J]. Acta Physica Sinica, 2016, 65(8): 219-231. |
| [9] |
ZENG J W, QIAN Y S, LV Z W, et al. Expressway traffic flow under the combined bottleneck of accident and on-ramp in framework of Kerner 's three-phase traffic theory[J/OL]. Physica A: Statistical Mechanics and Its Applications, 2021, 574: 125918. (2021-07-15) [2023-07-01]. https://doi.org/10.1016/j.physa. 2021.125918.
|
| [10] |
SUN S C, AN X, ZHAO J, et al. Modeling and simulation of lane-changing management strategies at on-ramp and off-ramp pair areas based on cellular automaton[J].
IEEE Access, 2021, 9: 35034-35044.
|
| [11] |
邓超, 刘港. 智能车辆连续换道模糊宽度学习决策模型[J]. 公路交通科技, 2025, 42(5): 36-42. DENG Chao, LIU Gang. Fuzzy broad learning system decision-making model for intelligent vehicle continuous lane-changing[J]. Journal of Highway and Transportation Research and Development, 2025, 42(5): 36-42. DOI:10.3969/j.issn.1002-0268.2025.05.004 |
| [12] |
潘芋燕, 张斌, 郭继孚, 等. 基于交通流基本图的过饱和交通状态道路阻抗函数[J]. 公路交通科技, 2025, 42(2): 1-12. PAN Yuyan, ZHANG Bin, GUO Jifu, et al. Road impedance function for oversaturated traffic state based on fundamental diagram[J]. Journal of Highway and Transportation Research and Development, 2025, 42(2): 1-12. DOI:10.3969/j.issn.1002-0268.2025.02.001 |
| [13] |
LARRAGA M E, ALVAREZ-ICAZA L. Cellular automaton model for traffic flow based on safe driving policies and human reactions[J].
Physica A: Statistical Mechanics and Its Applications, 2010, 389(23): 5425-5438.
|
| [14] |
LI X, LI X G, XIAO Y, et al. Modeling mechanical restriction differences between car and heavy truck in two-lane cellular automata traffic flow model[J].
Physica A: Statistical Mechanics and its Applications, 2016, 451: 49-62.
|
| [15] |
王凯. 基于元胞自动机的高速公路重载货车移动瓶颈研究[D]. 武汉: 华中科技大学, 2017. WANG Kai. Research on moving bottleneck of heavy trucks driving on freeways based on cellular automata[D]. Wuhan: Huazhong University of Science and Technology, 2017. |
| [16] |
蓝天飞. 基于元胞自动机交通堵塞车辆荷载模拟及在简支梁桥上应用[D]. 南昌: 华东交通大学, 2022. LAN Tianfei. Simulation of vehicle load in traffic jam based on cellular automata and its application in simply-supported beam bridge[D]. Nanchang: East China Jiaotong University, 2022. |
| [17] |
NAGEL K, SCHRECKENBERG M. A cellular automaton model for freeway traffic[J].
Journal de Physique I, 1992, 2(12): 2221-2229.
|
| [18] |
YANG D, QIU X P, YU D, et al. A cellular automata model for car-truck heterogeneous traffic flow considering the car-truck following combination effect[J].
Physica A: Statistical Mechanics and Its Applications, 2015, 424: 62-72.
|
| [19] |
FENG S M, LI J Y, DING N, et al. Traffic paradox on a road segment based on a cellular automaton: Impact of lane-changing behavior[J].
Physica A: Statistical Mechanics and Its Applications, 2015, 428: 90-102.
|
 2025, Vol. 42
2025, Vol. 42



 ,
,