0 引言

高速公路交织区作为连接合流区与分流区的关键过渡区域，通过辅助车道实现车辆路径转换，其动态交通特性直接影响路网通行效率与行车安全^[1-2]。该区域中车辆需在有限长度内完成频繁的车道变换与速度调整，导致车流紊动性显著增强，尤其在合流与分流点，多车协同避让与路径调整形成了高度复杂的交互场景^[3]。这种复杂性不仅使交织区事故率较普通路段高出30%~50%，更使其成为制约高速公路运行效率的核心瓶颈。在人机混合交通背景下，传统基于规则的自动驾驶系统难以应对交织区的动态交互，而人类驾驶员通过经验驱动的拟人化决策展现出的高效预测能力，为结合数据驱动方法优化自动驾驶系统提供了重要启示。深度学习技术通过挖掘海量交通数据中的时空规律，有望为交织区车辆决策提供更强大的支持，推动自动驾驶技术在复杂场景中的应用。

自动驾驶车辆轨迹预测研究主要采用基于规则和基于学习2种技术路线。

基于规则的方法通过物理模型、行为模型和交互感知模型进行预测。物理模型方面，Leu^[4]提出的扩展卡尔曼滤波器通过建立车辆运动学方程实现泊车轨迹的短期预测，能够实现较高精度的即时预测，但难以应对复杂交互场景；Abbas^[5]开发的多模型卡尔曼滤波器通过并行子模型提升突发状况下的鲁棒性；Chen^[6]提出的GPMM-TP算法结合IMM算法，通过高斯混合模型聚类和结构相似性分析，提升自动驾驶变道轨迹预测精度。行为模型关注换道意图识别，Liu^[7]提出了一种混合驱动的轨迹规划方法，结合运动预测与MPC实现安全高效的实时规划，并嵌入安全评估机制；David^[8]改进的HMM方法引入三阶段状态机提升识别率；张海伦^[9]提出基于稀疏表示的驾驶行为感知字典模型和意图识别框架，可识别6类驾驶行为，显著提高分类准确率。交互感知模型聚焦车辆间动态关系建模，Yan^[10]提出基于多车博弈论的交互建模框架，实现自动驾驶车辆的智能决策与路径规划；李文礼^[11]开发的SSA-GAN模型采用生成对抗网络架构，生成器基于五次多项式曲线规划安全行驶路径，判别器则评估轨迹的合理性和安全性，实现了横向和纵向运动的协同优化；Wang^[12]提出两阶段轨迹规划算法，通过交互编码和驾驶风格建模提升高动态路口场景的规划效能；齐龙^[13]融合驾驶风格分类与意图识别，试验表明其能有效提升轨迹预测精度，支撑合流区决策规划。

基于学习的方法利用数据驱动技术实现端到端预测。深度学习方法中，Gao^[14]提出的VectorNet采用层次图网络处理矢量数据避免信息损失；Liang^[15]开发的LaneGCN模型创新性地构建车道-车道拓扑图，通过图卷积网络提取车道级结构特征，再与车辆历史轨迹特征融合处理，显著提升了变道轨迹的预测准确性；Wang^[16]通过结合图注意力机制和多层门控网络的优势，实现了对车辆变道意图和轨迹的端到端学习；Zhao^[17]设计的DenseTNT通过密集采样与最优运输算法实现端到端预测。注意力机制方法方面，Zhou^[18]开发的HiVT框架采用分层Transformer结构，底层处理局部几何特征，高层建模全局交互关系，通过逐步聚合不同尺度的信息，在保持精度的同时将参数量减少40%；Xu^[19]设计的Transformer模型使用自注意力机制，能系统地确定车辆相互作用对目标车辆未来轨迹的影响；Zhang^[20]提出的ASTNAT采用非自回归解码避免误差累积；Wang^[21]提出了一种车道Transformer，用注意力模块取代轨迹预测模型中图卷积网络，在保持准确性的同时大幅降低了时间成本。强化学习方法中，金彦亮^[22]开发的Meta-VWG整合变分自编码器与元学习加速收敛；姚悦^[23]提出的RPPO算法创新性地将LSTM网络与移动翻转瓶颈卷积结合，通过循环策略梯度更新机制，显著提升了智能体对动态环境的适应能力；Lee^[24]设计的SLAC通过潜在行动者-评论家架构，利用潜在变量模型对环境不确定性及复杂观测数据建模，显著提升样本利用效率，达到了在复杂环境下使智能体学习到更具有鲁棒性的策略、获得更高累计奖励且提升策略稳定性与泛化性的效果。

综上，基于规则的运动预测方法具备高可解释性、稳定性和计算简便等优势，适用于快速响应和精确控制，但在复杂性、短时预测、灵活性、维护成本及泛化能力方面存在局限，尤其在处理复杂场景和异常情况时面临瓶颈。高速公路交织区作为交通流耦合核心区域，其轨迹预测面临多主体变道随机性、高密度车流时变性及驾驶行为异质性等挑战。基于学习的方法凭借出色的数据挖掘与特征提取能力，更适应该类复杂场景。传统GNN受限于静态结构，难以应对动态交互；GraphSAGE通过归纳式聚合与分层采样动态构建交互图，有效捕捉多跳空间相关性，适用于大规模混行交通；Transformer因计算复杂限制实时性，Informer通过高效和概率稀疏注意力机制提升长序列处理效率与预测精度，更适用于复杂交通中的轨迹预测任务。

基于GraphSAGE和Informer协同建模，本研究内容聚焦在以下方面：

(1) 针对高速公路交织区复杂场景，提出融合GraphSAGE与图注意力网络(GAT)的换道意图识别模型。通过动态构建无人车与邻近交通车辆间的交互拓扑关系，利用多头注意力机制捕捉车辆间的竞争-协作关系，并结合敏感特征，实现对换道意图的精准识别。该模块为后续轨迹预测提供语义先验知识。

(2) 为适应交织区场景的长时预测需求，对Informer模型进行针对性改进。采用概率稀疏自注意力机制降低计算复杂度，同时引入时序蒸馏模块提取关键运动特征，在保证无人车辆轨迹预测精度的前提下显著提升长时域预测的效率与稳定性。

(3) 设计双向门控融合策略实现意图识别与轨迹预测深度耦合。在空间维度，意图向量动态调节图注意力权重，强化对关键交互车辆的特征提取；在时间维度，将意图概率分布嵌入解码过程，生成符合驾驶行为语义的多模态预测轨迹，实现物理约束与行为合理性的统一。

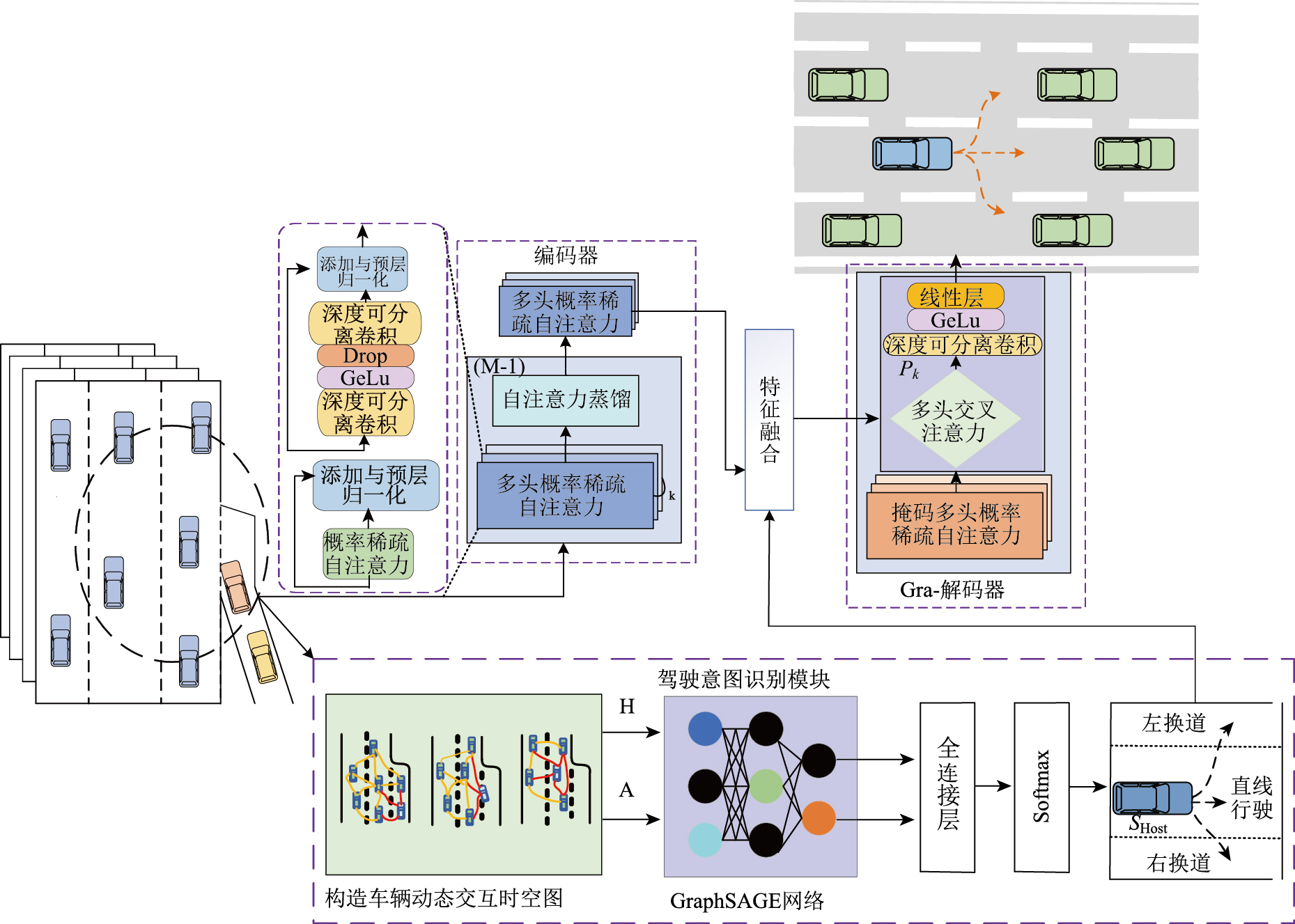
1 Gra-Informer模型框架

在自动驾驶领域，精准的换道意图识别与轨迹预测的协同优化是提升系统性能的核心。本研究提出的Gra-Informer模型(图 1)通过深度融合图神经网络与Informer的互补优势，构建了意图感知的轨迹预测模式。具体而言，GraphSAGE模块生成的换道意图向量并非独立输出，而是作为时空上下文特征被动态注入Informer的编解码流程。当GraphSAGE识别到某车辆存在换道意图时，其输出的高维嵌入表示会通过可学习的特征门控权重矩阵W^(k)与轨迹编码器的时空注意力层交互：在编码阶段，意图向量通过拼接操作与历史轨迹特征融合，并通过概率稀疏自注意力机制动态筛选关键查询向量，重新校准注意力权重，强化对转向、横向位移等意图相关特征的提取；在解码阶段，该向量作为先验知识通过外积操作与交互特征H_interact融合，参与跨步注意力计算，指导模型在生成未来轨迹点时侧重潜在换道方向的概率分布。当右换道概率大于设定的阈值时，门控信号会增强右侧车道邻近车辆的交互权重，并抑制无关车辆特征，驱动解码器生成向右偏转的候选路径。这种耦合机制使得Informer的预测轨迹在物理连续性基础上，进一步体现换道意图的语义合理性。例如当检测到邻车强烈的右换道意图时，预测轨迹会在保持运动学平滑的同时，提前生成向右偏转的候选路径。试验表明，引入意图向量后，预测轨迹与真实轨迹的横向误差在换道临界点有明显改善，验证了两模块通过动态门控与概率稀疏注意力协同实现的交互有效性。

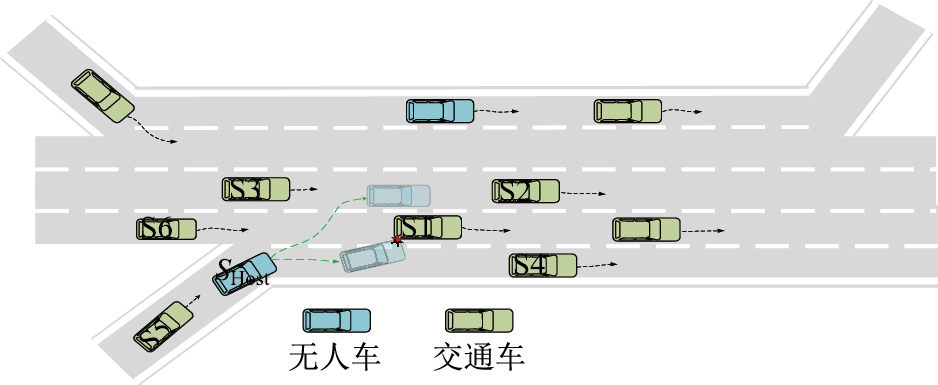
图 2所示为高速公路交织区无人车与交通车辆混行场景，在这一过程中，目标车辆(无人车)S_Host的换道意图和轨迹预测不仅受到其自身的状态影响，还直接受到其邻近交通车辆的动态交互作用的影响。因此，本研究提出的模型将综合考虑目标车辆及其邻近交通车辆的状态参数，作为输入数据。这些参数包括速度、加速度、位置、方向等关键动态特征。基于多车交互动态特征输入，本研究采用Gra-Informer模型，通过编码车辆间的拓扑关系与时序依赖性，实现对目标车辆换道意图的识别及其未来轨迹的预测，以此作为车辆决策系统的关键输入，为其运动规划与控制提供可靠的态势感知依据。

令I^(t)为目标车辆及邻近交通车辆的历史状态参数矩阵，如式(1)所示。其中，S_i^(t)为第i辆车的属性，代表t时刻位于不同位置的车辆i的状态信息，其中i的取值分别为1~6，如公式(2)所示。这些状态信息包括车辆在t时刻的横坐标x^(t)、纵坐标y^(t)、绝对速度v^(t)以及加速度a^(t)，此外，L、W和θ_i^(t)分别代表车辆的长度、宽度和航向角。T示历史时域的最后时刻，T_p代表历史时域，如式(3)所示。对于预测部分，公式(4)所示，O^(t')是在未来t'时刻预测的轨迹坐标，而X^(t')和Y^(t')分别代表在未来t'时刻预测的横坐标和纵坐标。T_d表示预测时域。

$ I^{(t)}=\left(S_{\text {Host }}^{t}, S_{1}^{(t)}, S_{2}^{(t)}, S_{3}^{(t)}, S_{4}^{(t)}, S_{5}^{(t)}, S_{6}^{(t)}\right), \\ $

(1)

$ S_{i}^{(t)}=\left(x^{(t)}, y^{(t)}, v^{(t)}, a^{(t)}, L, W, \theta_{i}^{(t)}\right), i \in[0, 6], $

(2)

$ t=\left(T-T_{\mathrm{p}}, \cdots, T-1, T\right), $

(3)

$ O^{\left(t^{\prime}\right)}=\left(X^{\left(t^{\prime}\right)}, Y^{\left(t^{\prime}\right)}\right), t^{\prime}=\left(T+1, T+2, \cdots, T+T_{\mathrm{d}}\right)。$

(4)

为提升模型在复杂交通场景下的泛化能力，本文提出多层级鲁棒性保障机制。针对邻域车辆缺失的稀疏交互场景，构建可微分虚拟节点集合S_∅^(t)=[x_inf, y_inf, 0, 0, 0, 0]，其中x_inf=y_inf=10⁴，其与目标车辆S_Host的交互边权重e_Hφ^(t)通过距离敏感函数式(5)动态计算。

$ e_{H \varphi}^{(t)}=\exp \left(-\gamma\left\|\Delta p_{H \varphi}^{(t)}\right\|_{2}\right) \cdot \Pi\left(\left\|\Delta p_{H \varphi}^{(t)}\right\|_{2} \leqslant \tau\right), $

(5)

式中，$\gamma$为衰减函数；$\Delta p_{H \varphi}^{(t)}$为$t$时刻目标车辆位置$\left(x_{H}^{(t)}, y_{H}^{(t)}\right)$与虚拟节点($x_{\mathrm{inf}} y_{x \mathrm{inf}}$)的相对位置差，即$\Delta p_{H \varphi}^{(t)}=\left[x_{H}^{(t)}-x_{\mathrm{inf}}, y_{H}^{(t)}-y_{\mathrm{inf}}\right], \|\cdot\|_{2}$为计算二者平面距离的欧几里德范数；П(·)为指示函数，当$\left\|\Delta p_{H \varphi}^{(t)}\right\|_{2} \leqslant \tau$成立时输出1，否则为0；$\tau$为自适应距离阈值，定义为历史时刻邻域车辆距离的$95 \%$分位数，即$\tau=$ Quantil $e_{0.95}\left(\left\{\left\|\Delta p_{H i}^{(t)}\right\|_{2}\right\}_{i=1}^{6}\right)$。在此引入梯度门控掩码$m_{i j}^{(t)}=\Pi\left(\left|\frac{\partial L}{\partial e_{i j}^{(t)}} \cdot e_{i j}^{(t)}\right|>\eta\right)$实现无效边的自适应剪枝，其中，$m_{i j}^{(t)} \in\{0, 1\}$用于标记边$e_{i j}^{(t)}$是否保留，$e_{i j}^{(t)}$为车辆$S_{i}$与$S_{j}$在时刻$t$的交互权重。最终通过复合损失函数$L_{\text {robust }}= 0.2\left\|\boldsymbol{H}^{(t)}{ }_{\text {intent }}-\boldsymbol{H}_{\text {intent }}^{(t-1)}\right\|_{\mathrm{F}}^{2}+0.1 \operatorname{Var}\left(\left\{e_{i j}^{(t)}\right\}_{i j}\right)$约束特征平滑性与交互稳定性，其中$\boldsymbol{H}_{\text {intent }}^{(t)}$为$t$时刻的意图特征向量，由换道意图识别模块输出。

2 换道意图识别预测模块

高速公路交织区呈现高动态、高风险特性，其交通流具有多源汇聚、时空压缩的显著特征。该区域多车流在有限空间内需同步完成速度协同与车道切换，形成复杂的博弈决策场景：驾驶员需实时解析周边车辆轨迹意图并进行动态交互，而合流瓶颈、速度差干扰及认知负荷叠加效应进一步加剧了事故风险。在此环境下，无人车需依托长时域轨迹预测能力，在极短时间内完成多模态风险评估与安全轨迹生成。此时，对无人车换道意图的长时域预测能力显得尤为重要。

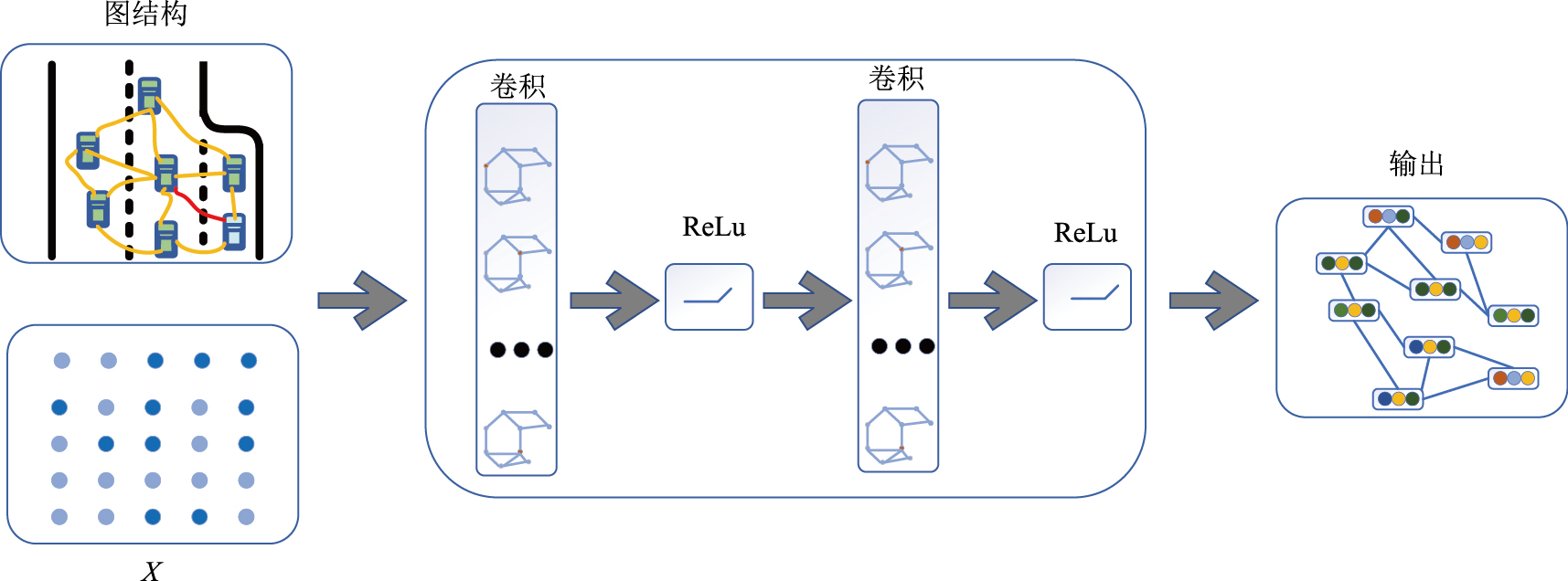
2.1 图神经网络工作原理

图神经网络通过节点间信息聚合机制在图结构数据建模中展现出显著优势，但其全图遍历模式在大规模场景下存在计算效率瓶颈，资源消耗随节点规模呈指数级增长，图神经网络的工作原理如图 3所示。本研究针对高速公路交织区动态交通场景的实时性需求，采用GraphSAGE框架实现高效拓扑特征提取。该模型通过可扩展的车辆间的邻居采样与层次化聚合策略，在降低计算复杂度的同时保持空间依赖建模能力，摒弃传统全图计算范式，以局部子图采样构建动态交互表征，为混行交织区车辆换道意图预测提供轻量化的边缘计算解决方案。

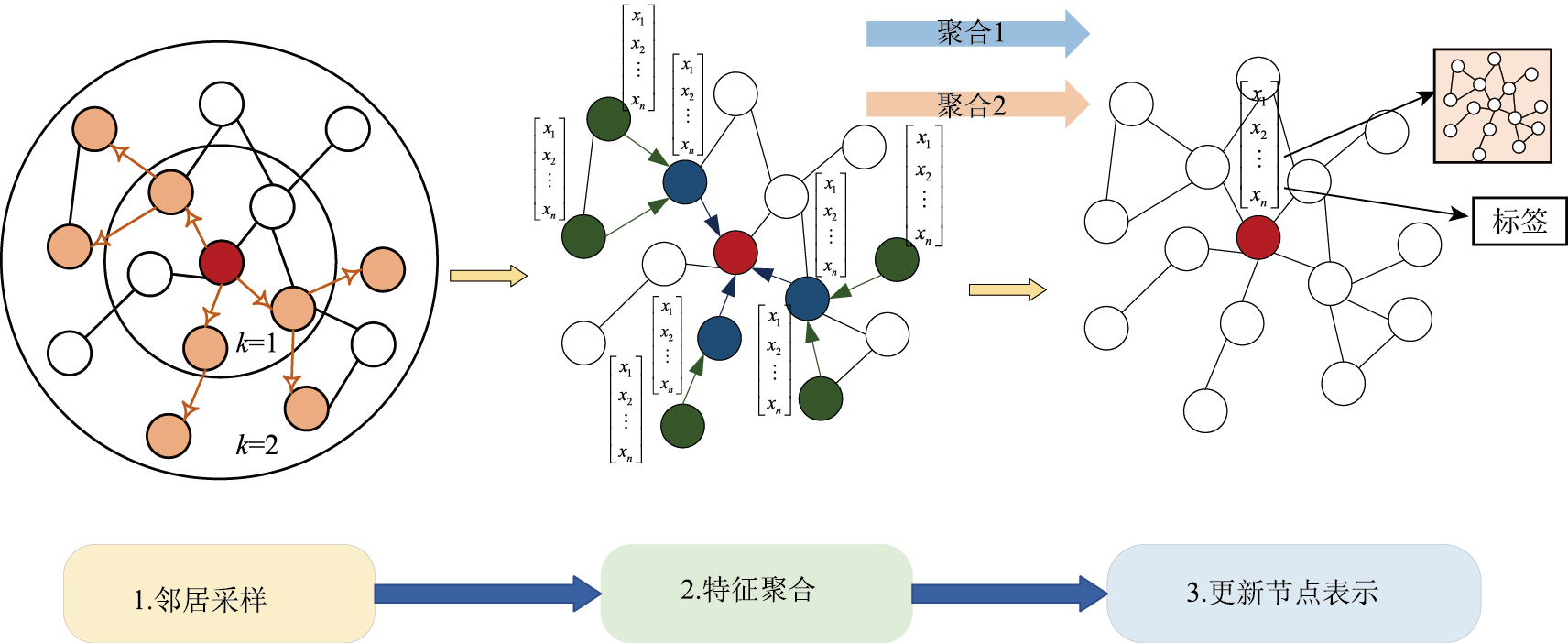
GraphSAGE算法通过迭代聚合局部邻居信息实现节点表示学习，如图 4所示，其核心流程包含以下3部分：邻居车辆节点采样、车辆特征聚合及邻居车辆节点表示更新。

在高速公路交织区的交通流建模中，邻居采样阶段可类比为对目标车辆周围的邻近交通车车流状态进行局部感知。针对目标车辆，从其邻居节点(设为n)中随机采样固定数量的车辆作为交互对象；若邻近车辆数量不足，采用有放回抽样补足样本，否则通过无放回抽样减少冗余计算。特征聚合阶段则通过均值或最大池化操作整合邻居车辆的运动特征(如速度、加速度)，其中均值聚合如式(6)所示，计算目标车辆与邻近交通车特征的加权平均，以刻画车流协同性：

$ \begin{gather*} \boldsymbol{h}_{v}^{(k)}=\sigma\left\{\boldsymbol { W } ^ { ( k ) } \cdot \operatorname { M E A N } \left[( \boldsymbol { h } _ { v } ^ { ( k - 1 ) } ) \cup \left(\boldsymbol{h}_{v}^{(k-1)}, \right.\right.\right. \\ \forall u \in N(v))]\}, \end{gather*} $

(6)

式中，h_v^(k)为第k层车辆v的嵌入向量; σ为激活函数; N (v)涵盖目标车辆在交织区的有效邻域范围。最大池化聚合则提取邻近交通车辆特征的逐维度极值(式7)，并与目标车辆特征拼接后经非线性变换(式8)生成融合表征：

$ h_{N(v)}^{(k)}=\operatorname{MAX}\left\{\left[\sigma\left(W_{\text {pool }} h_{u}^{k-1}+b\right)\right], \quad \forall u \in N(v)\right\}, $

(7)

$ h_{v}^{(k)}=\sigma\left[\boldsymbol{W}^{(K)} \cdot\left(h_{v}^{(k-1)} \| h_{N(v)}^{(k)}\right)\right], $

(8)

其中，MAX操作可捕捉交织区车流的冲突特征(如急刹行为)，而向量拼接‖保留了目标车辆的个体属性。最终，通过参数矩阵W^(k)与激活函数σ动态更新车辆表示，该机制在保证计算效率的同时，实现了对交织区复杂交互的层次化建模，为交通流预测与管控提供可微分的嵌入表达。

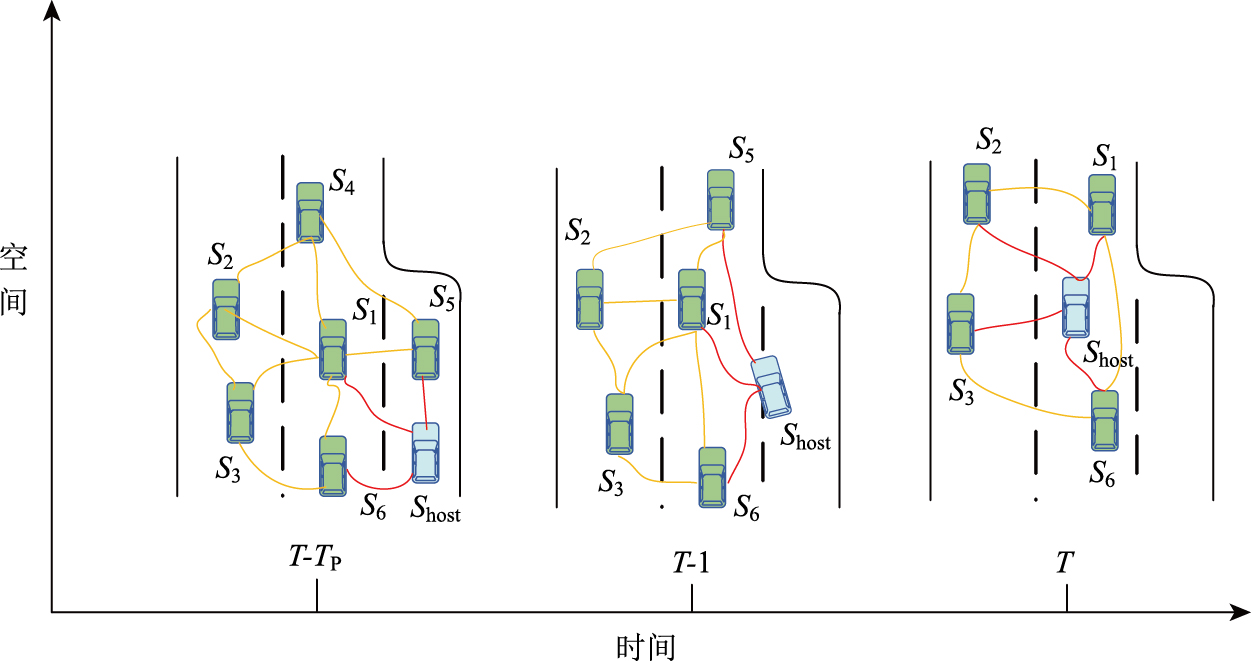
2.2 车辆动态交互时空关联关系

依据图 3能够清晰观测到，车与车间的动态交互特性呈现出时空关联的特性。结合图 2的复杂场景，可以建立描述多车间交互关系的时空关联图，如图 5所示。目标车辆及其邻近车辆之间的相互关系可以通过一个无向图G=(V, E)来表示。其中V={S₁^t, S₂^t, …, S₅^t, S₆^t}代表车辆节点的集合；E= {E_S0^tS1^t, E_S0^tS2^t, E_S0^tS3^t, …, E_S5^tS6^t} 代表车车关系之间的集合，其每条边E_Si^tSj^t的权重由邻接矩阵A量化。

在给定的t时刻，将目标车辆的特征矩阵H以及目标车辆与邻近交通车之间的邻接关系矩阵作为输入数据。其中特征矩阵的变量S_i^(t)为交互车辆的位置(x^(t), y^(t))、速度v (t)、加速度a (t)、长度L、宽度W和航向角θ等动静态特征变量。交互规律特征由图神经网络编码获得。

$ \begin{gather*} \boldsymbol{H}^{0}=\left[\begin{array}{l} S_{\text {Host }}^{\left(T-T_{\mathrm{P}}\right)} \\ S_{1}^{\left(T-T_{\mathrm{P}}\right)} \\ \vdots \\ S_{5}^{(T)} \\ S_{6}^{(T)} \end{array}\right]=\left[\begin{array}{ccccccc} x_{S_{\text {Host }}^{\left(T-T_{\mathrm{P}}\right)}} & y_{S_{\text {Host }}^{\left(T-T_{\mathrm{P}}\right)}} & v_{S_{\text {Host }}^{\left(T-T_{\mathrm{P}}\right)}} & a_{S_{\text {Host }}^{\left(T-T_{\mathrm{P}}\right)}} & L_{S_{\text {Host }}^{\left(T-T_{\mathrm{P}}\right)}} & W_{S_{\text {Host }}^{\left(T-T_{\mathrm{P}}\right)}}^{\left(T-T_{\mathrm{P}}\right)} & \theta_{S_{\text {Host }}^{\left(T-T_{\mathrm{P}}\right)}}^{\left(T-T_{\mathrm{P}}\right)} \\ x_{S_{1}}^{\left(T-T_{\mathrm{P}}\right)} & y_{S_{1}}^{\left(T-T_{\mathrm{P}}\right)} & v_{S_{1}}^{\left(T-T_{\mathrm{P}}\right)} & a_{S_{1}}^{\left(T-T_{\mathrm{P}}\right)} & L_{S_{1}}^{\left(T-T_{\mathrm{P}}\right)} & W_{S_{1}}^{\left(T-T_{\mathrm{P}}\right)} & \theta_{S_{1}}^{\left(T-T_{\mathrm{P}}\right)} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_{S_{5}}^{(T)} & y_{S_{5}}^{(T)} & v_{S_{5}}^{(T)} & a_{S_{5}}^{(T)} & L_{S_{5}}^{(T)} & W_{S_{5}}^{(T)} & \theta_{S_{5}}^{(T)} \\ x_{S_{6}}^{(T)} & y_{S_{6}}^{(T)} & v_{S_{6}}^{(T)} & a_{S_{6}}^{(T)} & L_{S_{6}}^{(T)} & W_{S_{6}}^{(T)} & \theta_{S_{6}}^{(T)} \end{array}\right] \end{gather*} $

(9)

$ \begin{gather*} \boldsymbol{A}=\left[\begin{array}{cccccc} a_{S_{\text {Host }}^{\left(T-T_{\mathrm{P})}\right.} {S_{\text {Host }}^{\left(T-T_{\mathrm{P}}\right)}}} & a_{S_{\text {Host }}^{\left(T-T_{\mathrm{P})}\right.} S_{1}^{\left(T-T_{\mathrm{P}}\right)}} & \cdots & a_{S_{\text {Host }}^{(T-1)} S_{6}^{(T)}} & \cdots & a_{S_{\text {Host }}^{(T)} S_{6}^{(T)}} \\ a_{S_{1}^{\left(T-T_{\mathrm{P})}\right.} S_{\text {Host }}^{\left(T-T_{\mathrm{P}}\right)}} & a_{S_{1}^{\left(T-T_{\mathrm{P})}\right.} S_{1}^{\left(T-T_{\mathrm{P}}\right)}} & \cdots & a_{S_{1}^{(T-1)} S_{6}^{(T)}} & \cdots & a_{S_{1}^{(T)} S_{6}^{(T)}} \\ \vdots & \vdots & & & \vdots \\ a_{S_{6}^{(T-1)} S_{\text {Host }}^{(T)}} & a_{S_{6}^{(T-1)} S_{1}^{(T)}} & & & \vdots \\ \vdots & \vdots & & & \vdots \\ a_{S_{6}^{(T)} S_{\text {Host }}^{\left(T-T_{\mathrm{P}})\right.}} & a_{S_{6}^{(T)} S_{1}^{\left(T-T_{\mathrm{P}})\right.}} & \cdots & \cdots & \cdots & a_{S_{6}^{(T)} S_{6}^{(T)}} \end{array}\right] \end{gather*} $

(10)

$ \begin{gather*}a_{S_{i}^{(n)} S_{j}^{(n)}}==\left\{\begin{array}{cc} \exp \left(-\frac{d_{i j}(t)}{\gamma}\right) & \text { 若 } d_{i j}(t) \leqslant \theta_{\mathrm{th}} \text { 且 } i \neq j \\ 0 & \text { 则 } \end{array}\right\} \end{gather*}。$

(11)

邻接矩阵A每一项的具体计算过程如公式(10)所示，式中d_ij (t)为同一时刻两辆车的欧式距离，θ_th为交互距离阈值，本文设置为50 m，为了筛选有效交互邻居；为衰减系数，控制交互强度的空间敏感度。为显示时空演化机制，车辆位置通过运动学方程$x_i^{(t+\Delta t)}=x_i^{(t+\Delta t)}+v_i^{(t)} \Delta t+\frac{1}{2} a_i^{(t)}(\Delta t)^2$更新，驱动邻接矩阵A实时调整。近距离车辆权重趋近1，远距离趋近0，模型通过动态图拓扑捕捉交织区车流博弈与协作行为，为自动驾驶决策提供可解释的交互建模框架。

2.3 换道意图预测算法流程

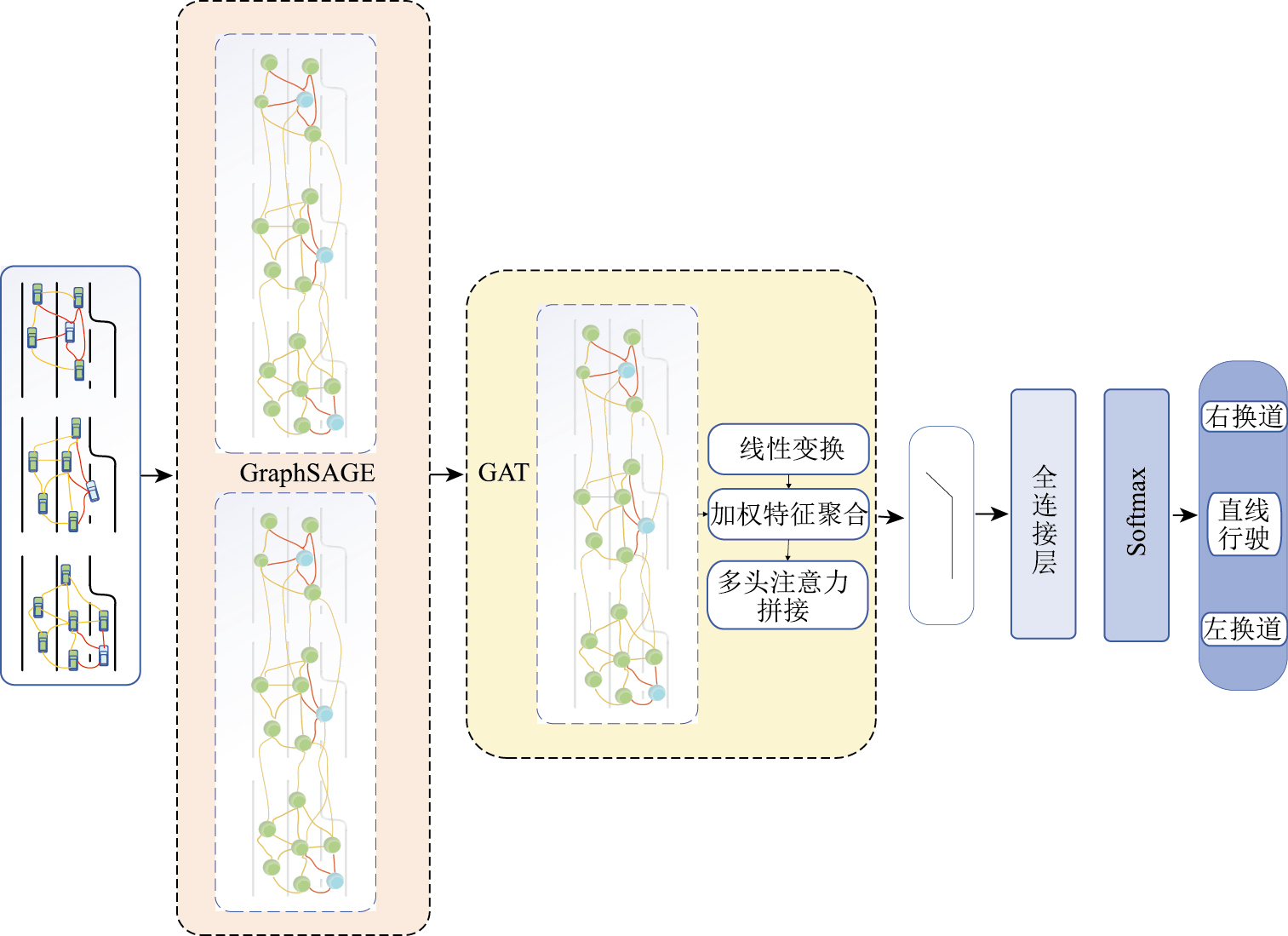
针对高速公路交织区车辆频繁变道、合流分流导致的动态交互特性与空间异质性，本研究构建了时空交互图模型，将特征矩阵H⁰和邻接矩阵A输入至融合GAT的GraphSAGE网络，实现对复杂车辆交互关系的自适应表征。该场景下GraphSAGE的归纳式学习能力可有效处理动态变化的道路拓扑结构，其基于采样的邻居聚合机制不仅能降低高密度车流环境下的计算复杂度，更通过注意力加权策略捕捉变道意图传导、跟驰行为传递等关键交互模式，为交织区特有的冲突博弈关系建模提供可解释的图表示基础，改进后的模型结构如图 6所示。

具体而言，在经过第1层GraphSAGE的邻居特征聚合和节点特征更新之后，对于第2层及之后的每一层，使用GAT的多头注意力机制。对于第i个注意力头，计算节点v与邻居节点u的注意力系数的计算过程如式(12)所示。其中Wⁱ为第e_jvⁱ个注意力头的科学系权重矩阵，aⁱ为第i个注意力头的注意力向量，‖表示特征拼接操作，LeakyReLU为激活函数。

$ e_{u v}^{i}=\operatorname{LeakyReLU}\left[\boldsymbol{a}_{i}^{\mathrm{T}}\left(\boldsymbol{W}^{i} h_{v}^{k-1} \| \boldsymbol{W}^{i} h_{u}^{k-1}\right)\right] 。$

(12)

归一化后的注意力权重α_uvⁱ如式(13)所示。

$ \alpha_{u v}^{i}=\frac{\exp \left\{\operatorname{LeakyReLU}\left[\boldsymbol{a}_{i}^{\mathrm{T}}\left(\boldsymbol{W}^{i} h_{v}^{k-1} \| \boldsymbol{W}^{i} h_{u}^{k-1}\right)\right]\right\}}{\sum\nolimits_{u^{\prime} \in N(v)} \operatorname{LeakyReLU}\left(\boldsymbol{a}_{m}^{\mathrm{T}}\left[\boldsymbol{W}^{i} h_{v}^{k-1} \| \boldsymbol{W}^{i} h_{u}^{k-1}\right]\right)} 。$

(13)

通过注意力权重加权聚合邻居节点特征，得到节点v在第k层的特征如式(14)所示：

$ h_{v}^{i, (k)}=\sigma\left(\sum\nolimits_{u \in N(v)} \boldsymbol{a}_{v u}^{i} \cdot \boldsymbol{W}^{i} h_{u}^{k-1}\right), $

(14)

其中，σ为非线性激活函数，最终节点v的多头注意力特征为所有注意力特征的拼接。

$ h_{v}^{(k)}=\operatorname{concat}\left(h_{v}^{1, (k)}, \cdots, h_{v}^{H, (k)}\right) \text {, } $

(15)

式中，concat(·)为拼接操作；H为注意力头数。全连接网络函数f_FC将多头注意力层的输出特征h_v^(k)映射到更高维空间，用于区分不同的换道意图。设全连接层的权重矩阵为W_FC，偏置为b_FC，则全连接层的输出z如式(16)所示。

$ z=f_{\mathrm{FC}}\left(h_{v}^{(k)}\right)=\boldsymbol{W}_{\mathrm{FC}} \cdot h_{v}^{(k)}+\boldsymbol{b}_{\mathrm{FC} } 。$

(16)

最后将式(16)中全连接层映射的信息z转换为式(17)中的输出概率矩阵P，其中z₁, z₂, z₃分别对应左换道、直行、右换道的得分；p_k(k=1, 2, 3)分别代表目标车辆左换道、直行、右换道的概率。

$ \begin{gather*} \boldsymbol{P}=\left(P_{k}\right)=\operatorname{Softmax}(z)= \\ {\left[\frac{\exp \left(z_{1}\right)}{\sum\limits_{j=1}^{3} \exp \left(z_{j}\right)}, \frac{\exp \left(z_{2}\right)}{\sum\limits_{j=1}^{3} \exp \left(z_{j}\right)}, \frac{\exp \left(z_{3}\right)}{\sum\limits_{j=1}^{3} \exp \left(z_{j}\right)}\right] }。\end{gather*} $

(17)

3 轨迹预测模块

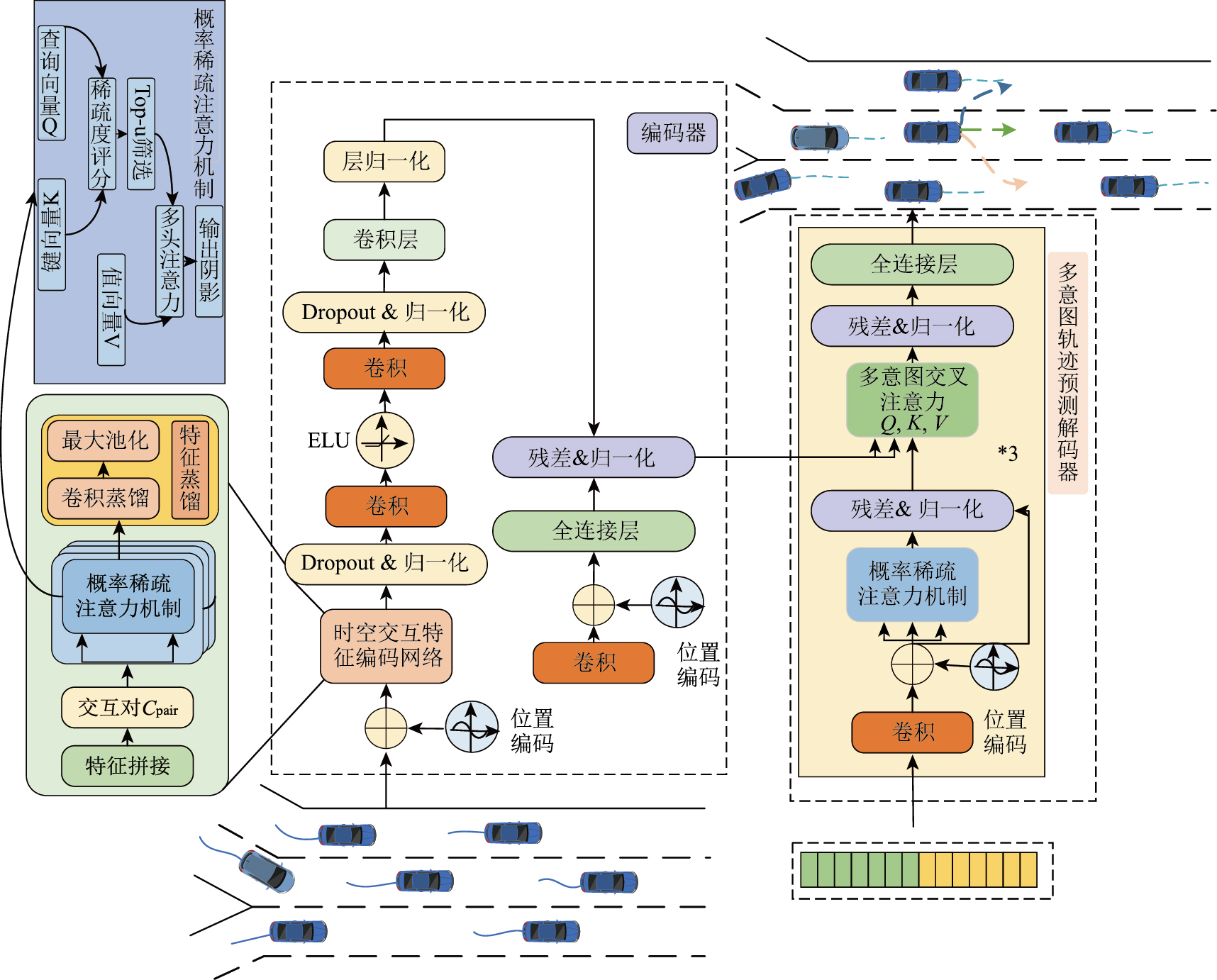
Informer模型基于Transformer编码器-解码器架构，针对长序列车辆轨迹预测任务，提出概率稀疏自注意力机制与自注意力蒸馏技术，显著降低计算复杂度并提升建模效率。进一步地，通过多意图轨迹解码器融合换道意图与交互信息，实现复杂交通场景下的多模态预测。模型框架如图 7所示，核心改进如下。

3.1 概率稀疏自注意力机制

在高速公路交织区，车辆频繁变道、合流分流导致动态交互复杂，传统自注意力机制需计算所有查询向量(Q)与键向量(K)之间的注意力权重，计算复杂度高O (L²)(L为序列长度)难以实时处理长序列轨迹数据。概率稀疏自注意力机制通过动态筛选关键查询向量，仅对部分查询进行完整计算，将复杂度降至O (Llog L)，同时保持预测精度。其核心步骤包括：(1) $\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}$向量生成：在高速公路交织区，目标车辆的查询向量$\left(q_{i} \in \boldsymbol{Q}\right)$可能包含其横向偏移和加速度信息，而邻近交通车($k_{i} \in \boldsymbol{K}$)的键向量则反映其相对速度和车道位置。通过式(18)的映射，模型将原始特征转化为可量化的交互关系表示，为后续稀疏篮选提供基础；(2)稀疏性度量：利用$K L$散度(式19)量化查询向量$\boldsymbol{Q}$的信息量。在合流区，若目标车辆($q$)的横向速度突变(如($\Delta V_{x}>0.5 \mathrm{~m} / \mathrm{s}$))，其与切人车辆($k_{j}$)的交互强度$\frac{q_{i} k_{j}^{\mathrm{T}}}{\sqrt{d}}$显著高于其他车辆，导致$K L$散度$M\left(q_{i}, \boldsymbol{K}\right)$增大，该查询向量被保留为关键向量；(3)Top-$u$采样：筛选$K L$散度最高的前$u=c \cdot \ln L_{Q}$个查询向量，构建稀疏矩阵$\tilde{\boldsymbol{Q}}$；(4)稀疏注意力计算：在交织区，式(20)仅计算目标车辆与关键邻近交通车(如正在变道的车辆)的注意力权重，忽略远离车道或匀速行驶的车辆。例如，若$\tilde{\boldsymbol{Q}}$中仅保留1个关键查询(对应切入车辆)，则输出注意力权重集中反映该车辆的威胁程度，指导模型预测目标车辆的制动或加速意图。

$ \boldsymbol{Q}=X W_{Q}, \boldsymbol{K}=X W_{K}, \boldsymbol{V}=X W_{V}, $

(18)

$ M\left(q_{i}, K\right)=\ln \sum\limits_{j=1}^{L_{k}} \mathrm{e}^{\frac{q_{i} k_{j}{ }^{T}}{\sqrt{d}}}-\frac{1}{L_{k}} \sum\limits_{j=1}^{L_{K}} \frac{q_{i} k_{j}^{T}}{\sqrt{d}}, $

(19)

$ \operatorname{Attention}(\tilde{\boldsymbol{Q}}, \boldsymbol{K}, \boldsymbol{V})=\operatorname{Softmax}\left(\frac{\tilde{\boldsymbol{Q}}, \boldsymbol{K}^{T}}{\sqrt{d}}\right) \boldsymbol{V}(20) $

(20)

$ \begin{gather*} \boldsymbol{X}=\left[\begin{array}{cccccccccc} x_{1} & y_{1} & v_{1} & a_{1} & v_{x_{1}} & v_{y_{1}} & a_{x_{1}} & a_{y_{1}} & l_{i d 1} & \theta_{1} \\ x_{2} & y_{2} & v_{2} & a_{2} & v_{x_{2}} & v_{y_{2}} & a_{x_{2}} & a_{y_{2}} & l_{i d 2} & \theta_{2} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ x_{L} & y_{L} & v_{L} & a_{L} & v_{x_{L}} & v_{y_{L}} & a_{x_{L}} & a_{y_{L}} & l_{i d L} & \theta_{L} \end{array}\right] . \end{gather*} $

(21)

其中特征矩阵X∈R^L×d(L为序列长度，d含位置、速度、加速度等特征)表示历史时间步内所有车辆的状态信息，q_i∈Q为第i个查询向量，对应目标车辆在某一时间步的状态；k_i∈K表示第j个键向量，对应邻近交通车的状态；L_K为键向量的数量；$\sqrt{d}$表示缩放因子，防止点积值过大导致梯度不稳定；Q为筛选后的稀疏查询矩阵，仅包含KL散度最高的前u个查询向量。

3.2 时空交互特征编码网络

在高速公路交织区场景中，车辆频繁变道与合流行为导致交互关系高度动态化。在Informer模型的编码器中，时空交互特征编码网络通过概率稀疏自注意力机制与自注意力蒸馏技术协同建模车辆动态交互关系。输入为历史车辆状态矩阵X，对目标车辆v_ego，将其序列X_ego与每辆邻近交通车v_nearⁱ的序列X_nearⁱ沿特征维度拼接，生成交互对C_pairⁱ= [X_ego, X_nearⁱ]i∈ [1, N]，共构建N组交互对(N为邻近交通车数量)，表征目标车辆与所有邻近交通车的潜在交互关系。交互对通过可学习参数映射为Q/K/V向量，并基于KL散度筛选关键查询向量，抑制低交互强度噪声。稀疏注意力计算后，所有邻近交通车的输出经拼接与MLP融合为的交互特征向量H_interact。

为进一步压缩长序列并保留关键特征，编码器引入自注意力蒸馏技术：每层输出z^l通过一维卷积(核大小=3)与最大池化(步长=2)压缩序列长度，如式(22)所示，同时利用式(23)残差连接融合低层细粒度运动特征，防止信息丢失。最终输出的交互特征向量H_interact作为解码器核心输入，驱动多模态轨迹预测。其中，z^l+1为第l层编码器输出；Conv1D为一维卷积。

$ Z^{l+1}=\operatorname{Max} \operatorname{Pool}\left\{\operatorname{Conv} 1 \mathrm{D}\left[\operatorname{ELU}\left(Z^{l}\right)\right]\right\}+Z^{l}, $

(22)

$ H_{\text {interact }}=M L P\left[\text { Concat }\left(\text { Attention }{ }^1, \cdots, \text { Attention }{ }^n\right)\right]。$

(23)

3.3 多意图轨迹预测解码器

为应对高速公路交织区车辆的左转、直行及右转意图的多样性，设计的多意图轨迹预测解码器通过动态融合换道意图与交互特征实现多模态轨迹生成。解码器输入为编码器输出的交互特征向量H_interact及GraphSAGE生成的3类意图概率分布p_k, (k=1, 2, 3)。首先，如式(24)，通过可学习参数动态加权融合意图与交互信息：

$ F=\lambda \cdot P \otimes H_{\text {interact }}+(1-\lambda) \cdot H_{\text {interact }}, $

(24)

式中，⊗为外积操作，首先将3维意图概率扩展至交互特征空间，增强意图与场景的关联性。其次，融合后的特征F_adj经卷积与嵌入操作，并注入时序位置编码，生成适配解码器的输入特征F_adj。解码器包含左转、直行、右转3个独立子网络，共享编码器特征以减少计算冗余。每个子网络采用两级注意力架构：第1层通过概率稀疏自注意力机制筛选关键时间步(如左转意图中横向加速度突变的时间帧)，生成中间特征Y_mid；第2层以Y_mid为Query，编码器压缩特征H^T为Key/Value，通过交叉注意力融合全局上下文信息：

$ Y_{\mathrm{pred}}=\operatorname{Softmax}\left(\frac{Y_{\mathrm{mid}} H_{\mathrm{enc}}^{T}}{\sqrt{d}}\right) 。$

(25)

最终，通过全连接层将Y_pred映射为未来50步的轨迹坐标(k=1, 2, 3分别对应左转、直行、右转)，每步包含横向与纵向位置：

$ \hat{Y}_{k}=W_{\text {traj }} Y_{\text {pred }}+b_{\text {traj }} \quad(k=1, 2, 3), $

(26)

式中，W_traj为可学习参数矩阵；b_traj为偏置项。为同时优化多模态轨迹预测的多样性和意图一致性，设计了联合损失函数，核心由2部分组成：首先，多模态轨迹损失采用负对数似然(NLL)形式，通过高斯核相似度评估预测质量，如式(27)所示。

$ L_{\text {main }}=-\log \sum\limits_{k=1}^{3} p_{k} \exp \left(-\frac{\left\|\hat{Y}_{k}-Y_{g t}\right\|_{2}^{2}}{2 \eta^{2}}\right), $

(27)

式中，Y_gt为真实轨迹(含T步的x, y坐标)；$\hat{Y}_{k}$为第k类意图(左转/直行/右转)的预测轨迹；p_k是GraphSAGE输出的意图概率；η为温度系数。该损失通过概率加权(p_k)和高斯核exp(·)的联合设计，鼓励至少一个模态的轨迹接近真实值，同时平衡多模态竞争。其次，意图一致性约束损失强制预测轨迹与意图标签的空间对齐，如式(28)所示：

$ L_{\text {aux }}=\alpha \sum\limits_{k=1}^{3} \prod(k=g t) \cdot\left\|\hat{Y}_{k}-Y_{g t}\right\|_{2}^{2}, $

(28)

这里∏(k=gt)为示性函数(真实意图匹配时为1)，确保模型在特定意图分支上精准优化。总损失为加权和L=L_main+L_aux，通过平衡系数α调节意图约束的强度；‖·‖₂表示L范数，用于量化轨迹误差。

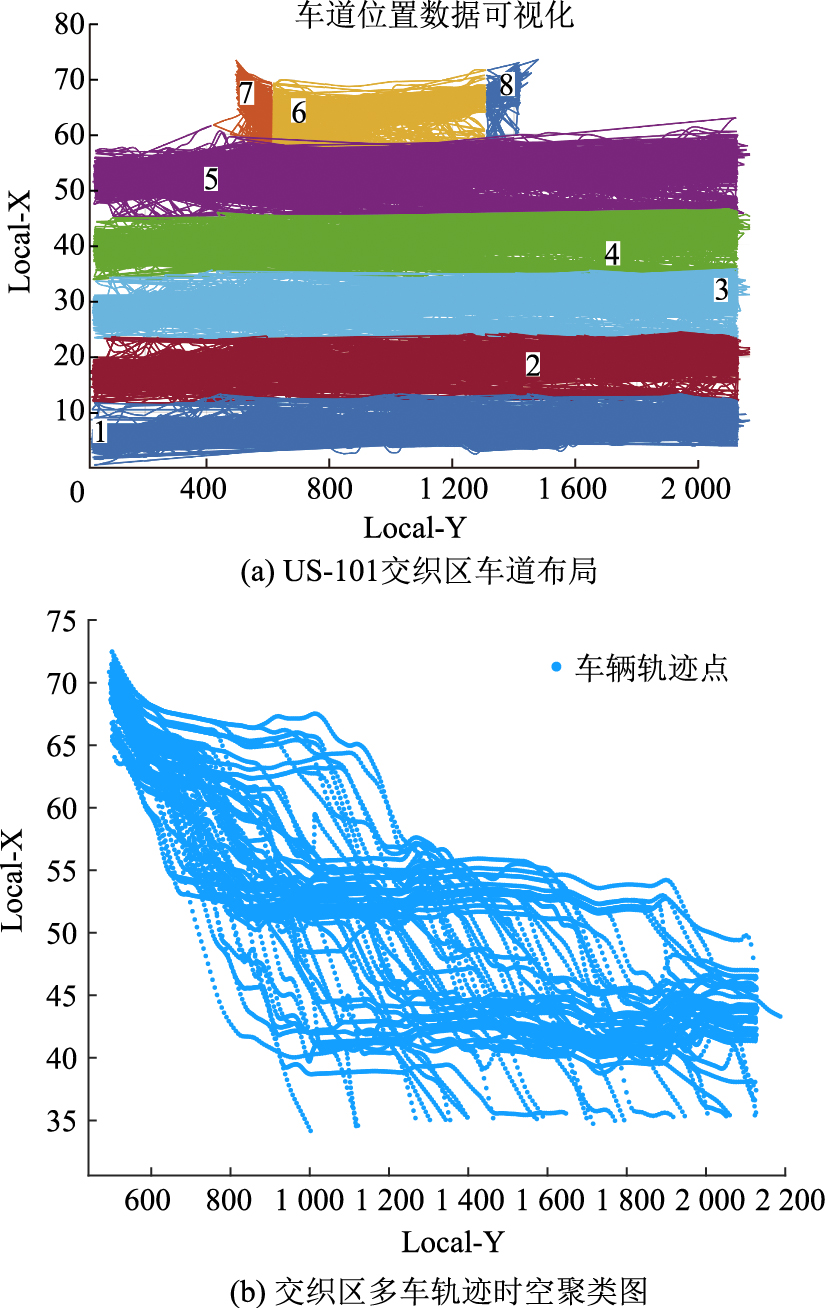
4 自然数据集处理与片段提取 4.1 NGSIM\US-101数据集

本研究采用NGSIM\US-101路段数据集，采集自洛杉矶高速公路南向5条主线车道及交织区，数据采样频率为10 Hz，涵盖15 min内交通流从畅通至拥堵的动态演变过程，如图 8所示。数据集包含丰富的车辆运动参数，为研究交织区复杂驾驶行为提供了可靠的数据基础。

在数据预处理阶段，首先对原始数据进行筛选和清洗。考虑到研究目标是小型乘用车的驾驶行为，我们剔除了摩托车和大型车辆的数据。同时，为聚焦交织区的典型驾驶行为，特别选取了主线车道5与加速车道6之间的并线区域，以及匝道7车辆汇入加速车道6的关键路段数据。筛选后的部分数据集如表 1所示。

4.2 数据误差分析

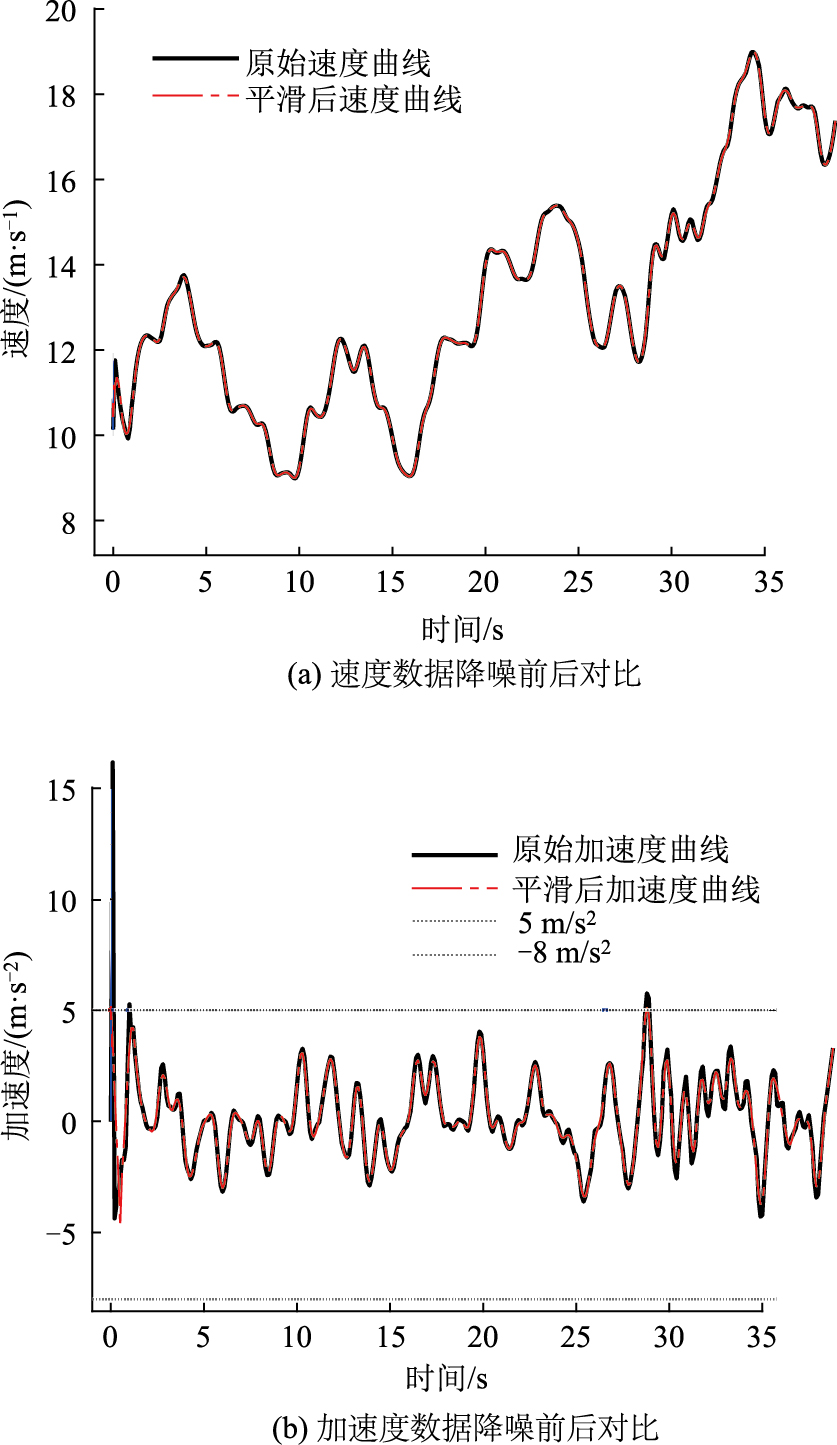
数据分析发现原始数据存在明显的噪声干扰，主要体现在2个方面：一是轨迹数据中的位置坐标抖动，特别是在车辆变道过程中横向位移出现不连续跳变；二是运动学参数的物理不合理性，包括速度的瞬时突变和加速度超出正常驾驶范围(如超过[― 8 m/s², 5 m/s²]的合理阈值^[25])。为消除这些噪声影响，采用S-G滤波器进行数据平滑处理，如图 9所示。该方法基于局部多项式最小二乘拟合，能够在保持信号主要特征的同时有效抑制随机噪声。为评估S-G滤波对车辆加速度特征的保留能力，本文建立了量化评价指标体系。S-G滤波的有效性通过系统的量化评价得到验证。基于峰值检测算法^[26]，采用滑动时间窗口宽度为9的3次多项式S-G滤波在抑制高频噪声的同时，较好地保持了速度、加速度信号的物理真实性与动态特征，其加速度突变事件的峰值保留率达到(92.3%±4.7)%，典型急刹车工况的正向峰值从5.78 m/s²保留为4.78 m/s² (保持率82.7%)。通过一阶导数分析进一步证实，信号动态变化率的平均保留率为(85.6±6.2)%，表明算法对加速度变化趋势具有良好保真度。

4.3 换道数据轨迹提取

在轨迹意图识别系统中，为实现驾驶行为的多模态分类(左换道、右换道、直线行驶)，提出基于运动学特征融合的变道行为时空联合检测方法。设轨迹片段为时间序列T={p(t)|t∈[t₀, t_n]}，其中p(t)=(x(t), y(t))表示时刻车辆在笛卡尔坐标系中的位置，该方法首先通过航向动力学模型建立运动学特征与变道行为的关联。具体地，航向角θ(t)由式(29)计算得到；其变化率κ (t)由式(30)得到，表征转向强度，定义为轨迹曲率。

$ \theta(t)=\arctan \left(\frac{\mathrm{d} y / \mathrm{d} t}{\mathrm{~d} x / \mathrm{d} t}\right) , $

(29)

$ \kappa(t)=\frac{\mathrm{d} \theta}{\mathrm{~d} t}=\frac{\ddot{y} \dot{x}-\dot{x} \dot{y}}{\dot{x}^{2}+\dot{y}^{2}}, $

(30)

式中，$\dot{x}=\mathrm{d} x / \mathrm{d} t, \quad \ddot{x}=d^{2} x / \mathrm{d} t^{2}$分别为位置的一阶和二阶运动学导数。基于此，变道行为的起止判定采用双约束条件：时序约束要求变道时长$\Delta T=t_{\mathrm{e}}-t_{\mathrm{s}} \leqslant T_{\text {max }}$，其中$T_{\text {max }}$为最大允许变道时长。而航向约束则要求$\exists \tau \in\left[t_{\mathrm{e}}-t_{\mathrm{s}}\right]$，使得累积转向量满足$\int_{t_{\mathrm{s}}}^{t_{\mathrm{e}}}|\kappa(t)| \cdot \mathrm{d} t \geqslant \theta_{\psi}$，同时式(31)曲率符号$\operatorname{sgn}(\kappa(t))$区分左换道与右换道。

$ \operatorname{sgn}(\kappa(t))= \begin{cases}+1 & \text { 左换道 } \\ -1 & \text { 右换道 }^{\circ}\end{cases} $

(31)

该方法通过自适应时间窗修正机制和多模态决策函数，当检测到变道持续时间超过阈值ΔT>T_max时，系统通过优化目标函数式(32)。动态调整时间窗口范围t' _s, t' _e，其中第1项惩罚窗口内曲率的整体偏离，第2项约束窗口长度以避免极端值。最终的分类决策函数由式(33)得到。

$ \min _{t_{\mathrm{s}}^{\prime}, t_{\mathrm{e}}^{\prime}}\left\|\frac{1}{t_{\mathrm{e}}^{\prime}-t_{\mathrm{s}}^{\prime}} \int_{t_{\mathrm{ss}}^{\prime}}^{t_{\mathrm{e}}^{\prime}} \kappa(t) \mathrm{d} t\right\|_{2}^{2}+\lambda\left(t_{\mathrm{e}}^{\prime}-t_{\mathrm{s}}^{\prime}\right), $

(32)

$ f(T)=\left\{\begin{array}{l} +1 \quad \text { if } \quad \mu_{k}>\theta_{+} \text {and } \sigma(k)<\zeta \\ -1 \quad \text { if } \quad \mu_{k}<\theta_{-} \text {and } \sigma(k)<\zeta, \\ 0 \quad \text { otherwise } \end{array}\right. $

(33)

式中，μ_k和σ (k)分别表示曲率的均值和标准差；θ₊、θ_-为方向阈值；ζ为运动平稳性阈值。该模型通过融合微分几何特征与统计模式分析，不仅增强了运动学解释性，还通过复合约束条件和优化理论方法显著提高了检测精度和自适应能力。

5 试验及数据分析 5.1 试验环境配置与模型参数

本研究提出的高速公路交织区车辆换道意图预测模型和车辆轨迹预测模型均基于PyTorch框架开发，在PyCharm集成开发环境下实现。实验平台配置为Windows 10操作系统，CPU为Intel Xeon W-2295，GPU为NVIDIA RTX A2000，利用CUDA 11.7加速计算。

本研究提出的意图识别模型采用GraphSAGE-GAT混合网络，通过3层GraphSAGE(256维)提取局部特征，3层GAT(8头注意力)建模车辆交互，使用Adam优化器(lr=0.001)和OneCycleLR调度，配合0.2 Dropout与混合精度训练，在300轮训练中达到较高准确率。轨迹预测部分使用Adam优化器，学习率lr=0.001，Batchsize=256，确保长时序预测的稳定性。这些超参数均经贝叶斯优化调参确定，在计算资源与模型性能间取得最优权衡。

5.2 换道意图识别试验及数据分析

为了验证本研究提出的基于GraphSAGE图神经网络的目标车辆换道意图识别模型的有效性，我们设计了对比试验，选取了30 229个历史驾驶样本数据，涵盖左转、直行和右转3种典型换道意图。试验采用五折交叉验证方法，将所提模型与CNN-LSTM、Bi-LSTM以及Mm-Transformer共3类主流换道意图识别的基准模型进行系统对比。各模型的识别性能指标如表 2所示，具体包括准确率、精确率、召回率和F1分数等关键评价指标，以全面评估模型的识别效果。试验结果表明，本研究提出的模型在各项指标上均展现出显著优势，特别是在处理复杂交互场景下的意图识别任务时表现出更强的鲁棒性和泛化能力。

本研究提出的改进GraphSAGE模型在换道意图识别中表现最优，整体准确率达到91.54%，相比Bi-LSTM提升8.86%，这得益于其图神经网络结构对车辆交互关系的有效建模；尽管CNN-LSTM在直行任务中取得最高精确率(97.27%)，但其综合性能仍不及GraphSAGE，而Mm-Transformer通过自注意力机制以89.45%的准确率超越CNN-LSTM，进一步验证了交互与时序特征融合对提升换道意图识别性能的关键作用。

混淆矩阵以矩阵形式直观呈现分类模型的预测结果与真实标签的对应关系，为评估模型在不同类别上的分类性能提供重要依据。如图 10所示，本研究提及的换道意图识别模型在左转、右转及直行3类任务中的分类效果通过混淆矩阵进行量化分析，其中矩阵列向量表示样本的真实类别，行向量对应于模型的预测类别分布。

精准且及时地识别目标车辆的换道意图并预测其未来运动轨迹，尤其在车辆实施变道行为前完成有效预判，可为决策规划提供关键的时间裕度，对于提升无人车智能决策系统的安全性能与可靠性具有关键意义。为验证模型性能，本研究从测试集中选取了一段左换道场景的车辆行驶数据，对其换道意图识别和轨迹预测结果进行了深入分析。如图 11所示，实时输出了车辆在接近车道线过程中3类换道意图的概率分布，这一动态识别结果为驾驶行为预测提供了重要依据。

如图 11所示，基于GraphSAGE网络的换道意图识别模型输出的左转概率起初仅为12.3%(直行概率为85.4%，右转概率为2.3%)，此时换道意图以直线行驶为主导。随着车辆靠近车道线，左转概率逐渐上升，当时距缩短至2 s时，左转概率增至58.7%(直行概率降至39.1%，右转概率为2.2%)。当车辆与车道线时距约为1.5 s时，左转意图概率突破阈值(设定为60%)，达到63.5%，系统判定车辆具有明确的左车道变换意图。车辆抵达车道线时，左转概率升至最高，而其他两类意图概率均降至最低。结果表明，基于Graph-SAGE网络的换道意图识别模型能够动态响应车辆行为变化，准确性高，可精准识别换道意图。

5.3 轨迹预测模型试验及性能对比

在水平方向预测评估中，本研究选取了BiLSTM、CNN-LSTM和Mm-Transformer这3种轨迹预测模型与模型Gra-Informer对比。这些深度学习模型均能通过非线性建模捕捉时序数据动态特征，并建立长期依赖关系。CNN-LSTM通过卷积层提取车辆空间拓扑特征结合LSTM捕捉时序的依赖，为轨迹预测提供时空联合表征；Bi-LSTM利用双向循环结构同步建模前后向时序特征，有效捕捉车辆运动惯性与趋势；Mm-Transformer基于多头注意力机制实现车辆间的动态交互，在复杂交通场景下的车辆协同轨迹预测表现优异。而Gra-Informer凭借概率稀疏自注意力机制与自注意力蒸馏策略，可有效解决长时序预测瓶颈，降低计算复杂度，提升长序列建模效率。本研究选择Informer作为核心对比模型，旨在验证其在超长序列场景下相较于传统混合模型与复杂多模态架构的优越性，特别是在保持预测精度的前提下解决内存消耗与计算效率的平衡问题。

如图 12所示，以换道点为参考点，向车辆行驶的反方向依次选取了3.0，2.4，1.8，1.2，0.6和0.0 s 6种不同的提前预测时域(t_pred)，以观察算法在不同tpred时的预测效果。试验结果表明，Gra-Informer在时空预测性能上具有明显优势。通过三维轨迹可视化分析可见，该模型在6种t_pred时对目标车辆的轨迹分布预测能有效逼近真实轨迹，尤其在换道点附近展现出更高的集中度和同步性。结合换道意图识别结果(图 10)进一步验证，Gra-Informer能够准确捕捉车辆运动中的时空关联特性，为复杂交通场景下的轨迹预测提供了更可靠的解决方案。

如图 13所示，通过雷达图对比分析各模型在不同预测时域的横纵向位置误差(MSE)，并结合表 3中的量化指标数据，可以得出以下结论：在短期预测中，各模型表现差异不显著，其中CNN-LSTM模型凭借其独特的卷积网络与LSTM协同架构，在1 s预测时取得0.41 m的ADE最优值；Bi-LSTM模型则通过双向时序建模展现其优势，1 s ADE为0.44 m；而Mm-Transformer模型依赖其多头注意力机制，1 s ADE达到0.39 m，接近Gra-Informer模型的0.32 m。

随着预测时域延长至3~5 s，如表 3所示，各模型性能出现明显分化：传统模型的预测误差显著上升，其中Bi-LSTM模型在5 s预测时的ADE高达3.18 m，CNN-LSTM模型为2.62 m；Mm-Transformer模型虽展现出一定的长期建模能力，5 s ADE为2.57 m，但其O (N²)的计算复杂度限制了实际应用。相比之下，Gra-Informer模型通过创新的概率稀疏自注意力机制将计算复杂度降至O (Nlog N)，并融合动态图拓扑建模技术，在5 s长时域预测中仍保持最优性能，较Bi-LSTM模型误差降低达33.3%。这些结果充分验证了Gra-Informer模型在复杂交通场景下的优越性能。

为了验证本文模型中的稀疏注意力机制相较于全注意力机制的优势，对比了2种方法在训练损失和验证损失上的表现。如图 14所示，稀疏注意力机制在训练损失14(a)和验证损失14(b)上均显著低于全注意力机制。这一结果说明，稀疏注意力机制通过减少冗余计算，能够在保持模型表达能力的同时，有效降低过拟合风险，从而在训练和验证集上均表现出更优的性能。因此，稀疏注意力机制在提升模型训练效率和泛化能力方面均优于全注意力机制，验证了其在减少计算复杂度和优化模型性能方面的显著优势。

本研究模型的推理时间如图 15所示，尽管Gra-Informer模型在换道意图预测任务中的推理时间比传统时序模型长约20%~35%，但其通过概率稀疏自注意力机制与GraphSAGE图神经网络的深度融合，在性能上展现出显著优势。这种结合不仅使模型能够有效捕捉长序列依赖和复杂的交通实体拓扑关系，还通过图结构的动态特征聚合增强了模型对噪声数据和未知场景的鲁棒性。Gra-Informer提供的注意力权重可视化和不确定性量化为自动驾驶系统的安全验证提供了可靠依据，使其在精度与安全性上的提升远超计算延迟带来的代价。未来可通过模型压缩技术进一步优化其计算效率，而不牺牲其核心性能优势。

6 结论

本研究构建的基于动态时空融合的无人车换道意图识别与轨迹预测模型，在高速公路交织区复杂场景的分析中彰显出卓越效能。该模型有机融合GraphSAGE强大的图结构建模能力与Informer出色的长序列时序预测能力，在目标车辆意图分类和轨迹预测任务中达成了高精度与强鲁棒性的良好平衡。试验数据有力佐证，在5 s预测时域内，模型的平均位移误差(ADE)相较于传统方法显著降低23.6%，终点预测误差(FDE)减少18.4%，换道意图识别准确率高达91.54%，相较于现有基准模型展现出显著优势。概率稀疏自注意力机制成功将长序列建模的计算复杂度从O (N²)优化至O (Nlog N)，同时动态交互特征的图结构建模进一步强化了模型对复杂交通场景的适应能力。然而，本研究模型的局限性主要体现在对特定交通场景的依赖性和跨地域适应性上，且在密集交叉路口等场景中预测性能可能存在下降；尽管通过概率稀疏注意力机制降低了计算复杂度，但在超大规模实时交通流中，模型的计算效率仍需进一步优化，以满足自动驾驶系统对低延迟的严苛需求。

后续研究将聚焦模型轻量化设计，借助知识蒸馏或模型剪枝技术在维持模型性能的同时有效降低计算负载；引入增量学习机制，通过在线学习使模型能够动态适应不断变化的交通场景和驾驶行为模式；拓展至多智能体协同领域，融入车路协同框架并整合基础设施数据，以增强模型的全局预测能力。