扩展功能
文章信息
- 武启宇, 闫亚杰, 郭昱, 王时贵, 武海全.
- WU Qiyu, YAN Yajie, GUO Yu, WANG Shigui, WU Haiquan
- 考虑初始缺陷的轴心受压杆件整体稳定承载力
- Overall stability bearing capacity of axially compressive strut considering initial defects
- 公路交通科技, 2025, 42(6): 133-142
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(6): 133-142
- 10.3969/j.issn.1002-0268.2025.06.014
-
文章历史
- 收稿日期: 2023-02-17
2. 山西电子科技学院, 山西 临汾 041099;
3. 山西五建集团有限公司, 山西 太原 030025
2. Shanxi Institute of Electronic Science and Technology, Linfen, Shanxi 041099, China;
3. Shanxi Fifth Construction Group Co., Ltd., Taiyuan, Shanxi 030025, China
随着材料、加工制作及安装技术的不断发展,木、钢-木、混凝土、钢等材料都曾被应用于桁架结构中。在城市建设速度加快、建设标准不断提高的背景下,人行天桥的建设节奏也随之加快,而其中采用桁架作为承重结构的人行天桥所占比例最高。当前钢结构人行天桥仍是主流选择,然而传统钢筋混凝土结构和钢结构在材料生产、结构加工、现场安装等环节存在耗能高的问题,而且桥梁服役环境条件较差,导致其在全寿命周期内的维护成本较高。
由于铝合金材料具有轻质高强、耐腐蚀性能好、维护成本低等特点,其在人行天桥中的应用逐渐增加。中国国内已建成的小跨径铝合金人行天桥多采用半开放式桁架结构,其上弦杆间无横向联系杆件。其中广泛使用的6061-T6铝合金材料有着与传统Q235钢材相近的屈服强度[1],但弹性模量却只有1/3,这使得铝合金桥梁易发生桁架面外的整体失稳[2]。近年来有学者对工字形、箱形截面的整体稳定进行了研究,得出了截面宽厚比对承载力的影响与合理的有限元模拟方法[3-4], 但就杆件的初始缺陷对整体稳定承载力的影响尚无系统性的分析。本研究对9种不同截面、11种杆件长度,进行4种初始弯矩和6种初始偏心下的有限元计算与稳定承载力理论分析。
1 桁架杆件 1.1 材料桁架杆件材质为铝合金6061-T6,根据《铝合金结构设计规范》(GB 50429—2007),取弹性模量为7×104 MPa,比例极限(即名义屈服强度)为240 MPa,小于抗拉屈服强度275 MPa[5]。因在实际使用过程中允许杆件部分进入塑性,为方便开展初始缺陷分析,本研究取杆件的最大应力上限为材料的屈服强度,采用线性应力-应变曲线进行分析计算。
1.2 构件参数工字形截面属于开敞式截面,便于通过螺栓、铆钉等连接件与其他构件进行连接。因此本研究分析的桁架杆件采用热挤压成型的工字形截面,如图 1所示。具体规格参考《热轧H型钢和剖分T型钢》(GB/T 11263—2024)中宽翼缘H型钢,选定9种方便节点连接且为桁架结构常用截面,构件截面参数取值如表 1所示。
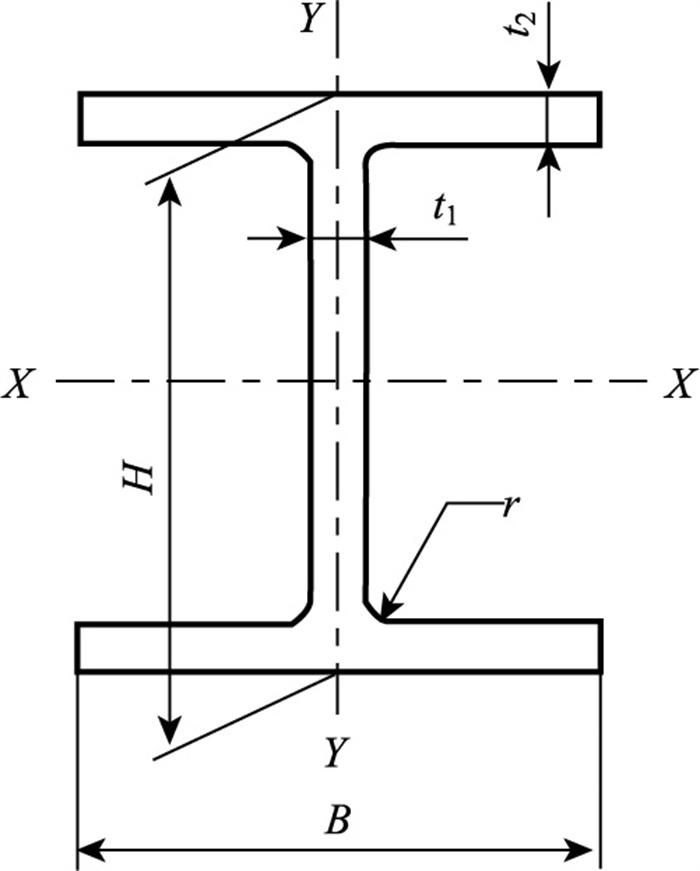
|
| 图 1 工字形截面参数 Fig. 1 Parameters of Ⅰ-shaped section 注:H为高度;B为宽度;t1为腹板厚度;t2为翼缘厚度;r为圆角半径;X-X为重心横向轴线;Y-Y为重心纵向轴线。 |
| |
| 型号 | 截面尺寸 | ||||
| B | H | t1 | t2 | r | |
| HW100 | 100 | 100 | 6.0 | 8 | 8 |
| HW125 | 125 | 125 | 6.5 | 9 | 8 |
| HW150 | 150 | 150 | 7.0 | 10 | 8 |
| HW175 | 175 | 175 | 7.5 | 11 | 13 |
| HW200 | 200 | 200 | 8.0 | 12 | 13 |
| HW250 | 250 | 250 | 9.0 | 14 | 13 |
| HW300 | 300 | 300 | 10.0 | 15 | 13 |
| HW350 | 350 | 350 | 12.0 | 19 | 13 |
| HW400 | 400 | 400 | 13.0 | 21 | 22 |
根据桁架受压杆件平面内外的计算长度,取杆件总长分别为1.0,1.5,2.0,2.5,3.0,3.5,4.0,4.5,5.0,5.5,6.0 m进行分析。铝合金构件加工方法主要为热挤压成型工艺,截面类型丰富,无焊接缺陷,材质均匀[6]。上述截面及长度基本涵盖小跨径铝合金人行天桥的杆件。
2 计算假定 2.1 失效标准桁架结构中工字形截面轴心受压杆件丧失承载能力的表现主要有位移超限和应力超限。其中位移限制采用GB 50429—2007给出的值,对于主体结构构件挠度的允许值不宜大于杆件总长的1/250;应力限制应当不超过6061-T6铝合金材料的抗拉、抗压和抗弯强度设计值200 MPa。因此,当轴心受压杆件的挠度或应力超过限制值时便被认为失效。
2.2 初始缺陷轴心受压杆件的初始缺陷主要包括构件安装前的初弯曲和在安装过程中的初偏心[7]。根据《铝及铝合金挤压棒材》(GB/T 3191—2019)规定,杆件的初弯曲不应大于0.001 5倍杆件长度,即0.15%。在本研究分析中取0.05%,0.10%,0.15%,0.20%。根据《铝合金结构工程施工质量验收规范》(GB 50576—2010),杆件的初偏心不应超过4 mm。实测值介于0.05%~0.20%之间,少数初偏心>0.20%[3]。因此在本研究分析时,取初偏心为0.05%,0.10%,0.15%,0.20%,0.25%。
2.3 边界条件已有相关研究结果[8]指出将杆件两端的连接忽略刚度,假定为铰接对桁架结构受力影响很小。特别是对于细长杆件, 节点处铰接连接形成的杵架与节点处刚接形成的桁架在除节点连接形式外的所有条件均相同的情况下, 2种桁架中杆件应力仅相差0.2%, 再者铝合金工字形截面杆件的桁架节点一般采用板式节点,弱轴方向的转动刚度为强轴方向转动刚度的0.095倍[9]。节点对弱轴方向的约束非常小,因此在本研究分析中假定杆件两端均为铰接。在满足上述计算假定前提下的计算简图如图 2所示。图中ΔL为初弯曲或初偏心[10],L为杆件实际长度,F为轴向施加于杆端的集中力。
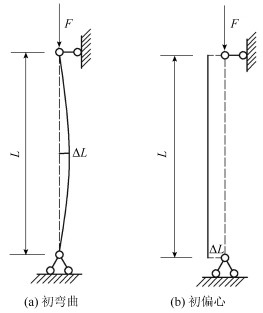
|
| 图 2 杆件轴心受力计算简图 Fig. 2 Calculation diagrams of axially compressive strut |
| |
3 有限元分析 3.1 杆件模型
采用有限元软件ABAQUS分析工字形截面轴心受压杆件的有限元计算模拟。为避免在模型计算过程中单元类型可能造成的不利影响,在分析中选取精度最高的C3D20单元[11]。工字形截面轴心受压杆件为整体建模,翼缘与腹板交汇处按表 1参数设置圆角。模型的初始弯曲取0.10%和0.15%。材料性能参数与构件尺寸参数分别参照1.1节和1.2节中的数据。边界条件设置为杆件一端约束杆件轴线方向和与杆件轴线垂直的2个方向的位移, 另一端约束与杆件轴线垂直的2个方向的位移,形成如图 2所示的铰接体系。
3.2 荷载作用工字形截面轴心受压杆件有限元模型的外力与初始弯曲均通过荷载作用的形式引入。首先建立无初始弯矩的计算模型,进行特征值分析,将得到的第1阶屈曲模态作为杆件的初始缺陷,屈曲特征值作为外荷载进行受力分析[12]。在计算过程中开启非线性分析,考虑变形对杆件承载能力的影响[13]。分析过程采用固定步长0.05,将轴心受压构件的应力与挠度达到限值时所对应外荷载中的较小值作为该杆件所能承受的极限外荷载。
3.3 分析结果具有0.10%初始弯曲和0.15%初始弯曲的HW100截面、6.0 m长杆件在弯曲过程中挠曲线内侧应力、挠曲线外侧应力、位移随外部荷载变化的曲线如图 3所示。

|
| 图 3 加载过程应力、挠度变化 Fig. 3 Stress and deflection variations during loading |
| |
由图 3可见,具有不同初始弯曲的杆件在应力、挠度方面均呈现如下规律。
(1) 在相对临界荷载小于0.8的情况下,应力与挠度均随着相对临界荷载的增大缓慢线性增大;在相对临界荷载大于0.8的情况下,随着相对临界荷载的增大,应力挠度快速增加且很快超过了材料设计强度200 MPa。应力快速增加是因侧向挠度所导致的高阶弯矩产生的弯曲应力所致。内侧与外侧的Mises应力不断增大反映出了在整个受力过程中内侧材料受压,外侧材料受拉,整个杆的受力状态更偏向于受弯而不是受压。
(2) 在相对临界荷载小于0.8的阶段,初始弯曲为0.10%的曲线比初始弯曲为0.15%的曲线要更平缓,斜率小;在相对临界荷载大于0.8的阶段,初始弯曲为0.10 %的曲线比初始弯曲为0.15%的曲线要更陡,斜率更大。初始缺陷越小,工字形截面轴心受压杆件的整体受力越呈现出脆性特征,在达到某一点时会迅速破坏。初始缺陷越大,杆件的整体受力会越呈现出延性的特征,变形趋向于在整个变形阶段内更加均匀,也更易在小外力时达到挠度限制条件。
此外,图 3也反映出杆件失效标准确定的合理性。对轴心受压杆件的挠度与应力同时进行控制可以使杆件有足够的安全储备,不易发生突然破坏。有限元分析结果还表明,具有初始缺陷的工字形截面轴心受压杆件的最大应力与最大弯矩均发生在杆件延长度方向的中点截面,其中最大应力点在发生弯曲后杆件的内侧边缘处。在后续分析过程中只需关注这一点。
4 轴心受压杆件承载力 4.1 理论方法在求解轴心受压杆件承载力时考虑非线性对结构承载力影响的方法一般包括增量法、迭代法、混合法、弧长法[14]。本研究计算承载力只需求得最终结果,无需考虑整个加载过程。因此综合各种方法的特点后最终选用迭代法计算。欧拉临界力计算公式[15]为:
| $ F_{\text {cr }}=\frac{\pi^2 E I}{L^2}, $ | (1) |
式中,Fcr为欧拉临界力;I为截面最小惯性矩;E为材料的弹性模量。
在3.1节中选取的所有杆件中,欧拉临界力最小为25.76 kN,如将外力精度控制为0.10 kN,相对误差已经小于0.39%,对于承载能力更大的杆件误差只会更小,所以将外力精度控制为0.10 kN已经能够满足分析要求。因此迭代法计算的过程中外力的控制精度确定为0.10 kN。
终止迭代计算的控制指标确定为:当前迭代计算所得应力除以当前计算所得总应力小于某一值时停止计算,此时认为计算所得总应力为准确值。通过试算发现,当该值控制为0.10%时与控制为0.01%时结果没有差别,此时每一步的增量已经很小,可认为已经计算完毕。所以终止迭代计算的控制指标确定为当前迭代计算所得应力除以当前计算所得总应力小于0.10%。
4.2 初始弯曲迭代分析在轴心受力杆件中定义距离杆端为x的截面挠度为y,则该截面的弯矩为:
| $ M(x)=F y, $ | (2) |
式中F为作用在杆件上的轴力(见图 2)。对于小变形,可得到挠曲线微分方程为:
| $ E I y^{\prime \prime}=-M(x)=-F y_{\circ} $ | (3) |
计算可得挠曲线方程为:
| $ y=A \sin \frac{\pi x}{L}, $ | (4) |
式中A为杆件挠度最大值。此时由于挠度而产生的弯矩为:
| $ M(x)=F y=F A \sin \frac{\pi x}{L} 。$ | (5) |
采用图乘法可以得出在此弯矩作用下杆件中点最大挠度为:
| $ y=\frac{M L^2}{\pi^2 E I}{ }^{\circ} $ | (6) |
在变形比较小的情况下,仍然可以认为其符合初始的挠曲线方程,只是最大挠度有所改变,此时挠曲线公式为:
| $ y=\frac{F A \sin ^2 \frac{\pi x}{L} L^2}{\pi^2 E I} 。$ | (7) |
重复以上步骤即可完成迭代计算。初始弯曲取值参考2.2节。利用Python建立上述过程的迭代计算程序[16]。计算结果中型号HW100、长度为6 m的杆件最终承载力为20.5 kN,该值与欧拉公式所得承载力的比值为79.72%。在Abaqus与Midas有限元计算中得到的承载力与欧拉公式所得承载力的比值为80.0%,二者比值相差0.28%,误差非常小。据此可认为工字形截面轴心受压杆件在应力、挠度二者限制下的变形符合小变形假设,且上述计算步骤所建立的程序可靠性良好。
将所分析的9×11共99种杆件尺寸信息统一为长细比,可得杆件中最大应力、最大挠度随长细比变化的曲线图。初始偏心为0.05%情况下工字形截面轴心受压杆件中的最大应力和最大挠度如图 4所示。

|
| 图 4 0.05%初始弯曲情况下的最大应力和最大挠度 Fig. 4 Maximum stress and deflection with initial bending of 0.05% |
| |
在长细比较小的阶段(长细比小于70),杆件首先在受压一侧的最大压应力达到了200 MPa,此时挠度偏小且挠度会随着长细比的增加而快速增加。此阶段的杆件稳定承载力的控制性因素为压杆的最大应力。对于长细比相差不大的杆件,长度较长的杆件在应力达到200 MPa限制值的情况下挠度偏大。
在长细比较大的阶段(长细比大于70),杆件稳定承载力的控制性因素就变为了压杆的侧向挠度,图 4中所示的挠度都已经达到了各自的限值,这种情况下杆件承载力取决于材料弹性模量等相关参数。因为杆件长度本身会有区别,从而图中挠度曲线会显示为锯齿形。随着长细比的增大,杆件可承受的最大应力会先迅速降低然后逐渐放缓,趋势类似于欧拉临界应力总图中的小柔度杆,这一降低的趋势与实际的杆长没有关系,仅取决于长细比。
在0.05%,0.10%,0.15%,0.20%这4种杆件初始弯曲下,2个阶段分界点对应的长细比分别为70.0,68.5,66.2,64.0。
因迭代计算较为繁琐,在设计阶段通常无法直接得出杆件在轴力作用下所产生的高阶应力。所以设计时的主要依据为外力除以总截面面积得出的名义应力,即迭代计算所得的临界应力。将杆件的迭代临界应力、欧拉临界应力、迭代临界应力÷欧拉临界应力所得的比例绘制到一幅图中(图中简称为比例),如图 5所示。为了三者能够较好地进行比较,欧拉临界应力在不是大柔度杆时偏安全,统一取200 MPa。由图可见,在长细比趋于0时,由迭代计算所得的临界应力趋于与欧拉临界应力相同。
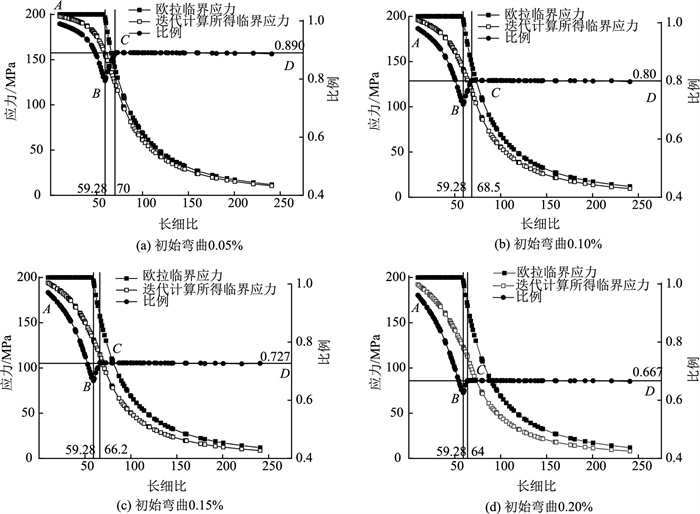
|
| 图 5 初始弯曲下的临界应力 Fig. 5 Critical stress with initial bending |
| |
如图 5(a)所示,在AB阶段杆件长细比小于59.28时,欧拉临界应力保持在200 MPa不变,但由迭代计算所得的临界应力会持续减小,并且曲线的斜率绝对值不断增大。
BC段杆件长细比超过了大柔度杆的界限,迭代计算所得的临界应力曲线没有明显的改变,仍然沿着原来的趋势在变化,但欧拉临界应力会因为适用公式的不同而快速降低。这样就导致了二者的比例反而有所增加,比例曲线在这一增加阶段较短,可视为线性。当长细比为B点值时,初始弯曲对承载力的影响最大,这一发现与相关研究结果[5]相同。
C点处杆件所对应长细比值即应力控制与挠度控制的分界点。CD段曲线中,迭代计算所得的临界应力曲线凹凸性发生了改变,下降的速率不再增加,而是在不断减小。CD段中2个应力的比值基本为一定值,并不会随着长细比的增加而明显改变。所以在这一阶段中迭代临界应力可以由欧拉临界应力公式计算值乘以一比例常数求得,如图 5所示。在杆件初始弯曲为0.05%,0.10%,0.15%,0.20%的情况下,这一比例常数分别为0.890,0.80,0.727,0.667。
由图 5可见,迭代计算所得的临界应力随着初始缺陷的增大在不断减小,而且随着初始缺陷的增大,BC段长度在不断降低。AB段比例曲线可以较好地用三次曲线进行拟合, 将这一段的比例设定为K1。
| $ K_1=A_1 x^3+B_1 x^2+C_1 x+D_1, $ | (8) |
式中,A1,B1,C1,D1为拟合参数(见表 2);λ为构件的长细比,x=0.01λ。
| 初始弯曲/% | A1 | B1 | C1 | D1 | R2 |
| 0.05 | -2.461 | 1.534 | -0.440 | 1.023 | 0.999 |
| 0.10 | -1.521 | 0.527 | -0.273 | 1.003 | 0.999 |
| 0.15 | -0.757 | -0.165 | -0.201 | 0.991 | 0.999 |
| 0.20 | -0.212 | -0.591 | -0.197 | 0.985 | 0.999 |
对于BC段比例曲线,可以在已知B点和C点对应长细比及比例值后线性插值得到。B点和C点的长细比及比例值见表 3。C点以后比例曲线可取定值。在计算不同杆件初始弯曲情况下的比例常数时可由上述数据计算所得的比例常数线性插值得出。
| 初始弯曲/% | B点 | C点 | |||
| 长细比 | 比例 | 长细比 | 比例 | ||
| 0.05 | 59.28 | 0.795 | 70.0 | 0.890 | |
| 0.10 | 59.28 | 0.719 | 68.50 | 0.80 | |
| 0.15 | 59.28 | 0.667 | 66.20 | 0.727 | |
| 0.20 | 59.28 | 0.626 | 64.0 | 0.667 | |
4.3 初始偏心迭代分析
在研究工字形截面轴心受压杆件时, 其稳定承载力受初始偏心的影响分析需考虑工况为: 杆件两侧支撑点均沿垂直于轴线方向产生等距偏移(见图 2(b))。此时杆件在沿长度方向内受一轴向力荷载与一均匀弯矩作用。对于这种情况下,杆件中每个截面的弯矩相同,则每个截面的曲率则应该相同,挠曲线的形式为一段圆弧,但通过挠曲线微分方程解得该挠曲线为一条抛物线。相关研究指出[17],在挠度为杆件长度1/100时,抛物线所对应的近似挠曲线与圆弧所对应的精确挠曲线仅相差0.01%。在本研究分析中杆件挠度最大取值为1/250,远小于示例中的1/100,因此采用抛物线作为挠曲线进行分析可以保证精度。
当在偏心荷载下的挠曲线为二次抛物线时,此时由弯曲所产生的二阶弯矩图为抛物线形式。由挠曲线微分方程可以得出在该弯矩作用下经过2次对x积分,挠曲线为四次抛物线。以此类推高阶挠曲线分别为2次曲线、4次曲线、6次曲线,高阶抛物线的面积及形心位置可通过积分求得。
同样按照4.2节迭代分析思路可建立Python程序。在Abaqus与Midas有限元计算中、施加相同外力情况下计算所得的承载力与程序计算所得的承载力差值为0.16%,证明所建立的程序可靠性良好。杆件初始偏心为0.05%下的最大应力和最大挠度如图 6所示。
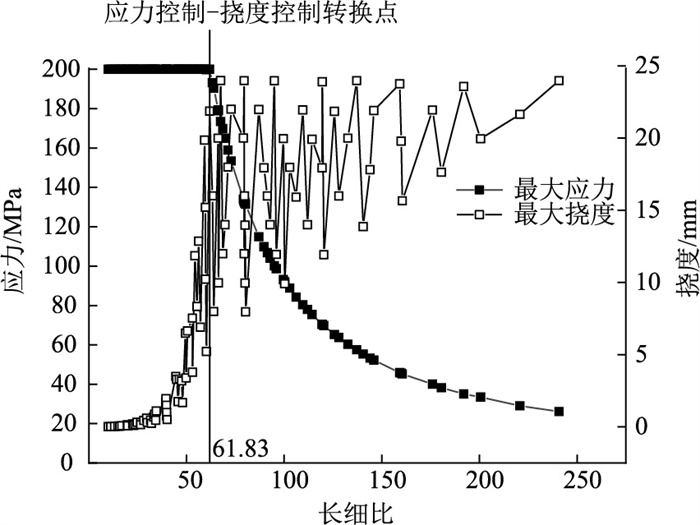
|
| 图 6 0.05%初始偏心情况下最大应力和最大挠度 Fig. 6 Maximum stress and deflection with initial eccentricity of 0.05% |
| |
杆件初始偏心情况下的图形基本与杆件初始弯曲情况下的图形(见图 4)规律相同。在长细比较小的阶段,杆件稳定承载力的控制因素为最大应力;在长细比较大的阶段,杆件稳定承载力的控制因素转变为杆件的侧向挠度。杆件初始偏心越大,应力控制与挠度控制的转换点所对应的长细比越小。杆件在0.05%,0.10%,0.15%,0.20%,0.25%共5种初始偏心情况下转换点对应的长细比分别为61.83,57.15,56.21,54.35,53.0。除了杆件初始偏心为0.05%时转换点对应长细比大于欧拉临界应力开始下降点对应的长细比59.28外,其余均低于59.28。为了设计阶段的应力选取,将杆件的迭代临界应力、欧拉临界应力、迭代临界应力÷欧拉临界应力所得的比例绘制到一幅图中,如图 7所示。
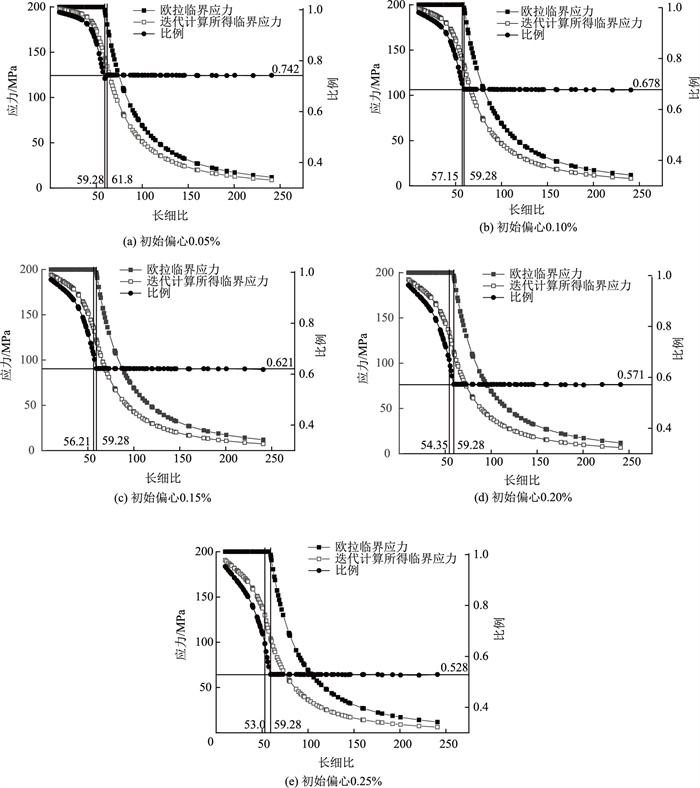
|
| 图 7 初始偏心临界应力图 Fig. 7 Diagrams of critical stress with initial eccentricity |
| |
在杆件初始偏心较小的阶段,欧拉临界应力开始发生变化点与杆件稳定承载力的应力、挠度控制变化点非常接近,使得长细比小于59.28时比例曲线呈现为平滑的曲线,且曲线上的值随着长细比的增加在不断减小。随着杆件初始偏心的增大,杆件稳定承载力的应力、挠度控制变化点在不断向左移动,使得这一点对应长细比接近或小于59.28,从而导致了在长细比超过59.28后比例曲线并不会有一段明显的上升段(见图 5),而是直接进入了平直阶段。下降段曲线可以同样较好地用三次曲线来进行拟合:
| $ K_2=A_2 x^3+B_2 x^2+C_2 x+D_2, $ | (9) |
式中A2,B2,C2,D2为拟合参数(见表 4)。
| 初始偏心/% | A2 | B2 | C2 | D2 | R2 |
| 0.05 | -5.372 | 3.867 | -0.976 | 1.060 | 0.999 |
| 0.10 | -3.791 | 2.295 | -0.635 | 1.026 | 0.999 |
| 0.15 | -3.282 | 1.857 | -0.618 | 1.018 | 0.999 |
| 0.20 | -3.578 | 2.184 | -0.802 | 1.026 | 0.999 |
| 0.25 | -4.122 | 2.726 | -1.030 | 1.037 | 0.999 |
在平直阶段,迭代临界应力可以由欧拉临界应力公式计算值乘以一比例常数求得,这一比例关系在图 8中比例曲线平直段标出,并可参照表 5。当杆件初始偏心介于0.05%,0.10%,0.15%,0.20%,0.25%时,可以按线性插值选取比例常数或偏安全地选取较大杆件初始偏心所对应比例常数。将表 3中C点比例与表 5中比例对比可发现在杆件具有相同的初始最大缺陷值下,初始偏心情况下的比例值将为初始弯曲情况下比例值的0.85倍左右,这说明初始偏心对于杆件的承载能力会更不利,应在实际工程应特别注意加以限制。
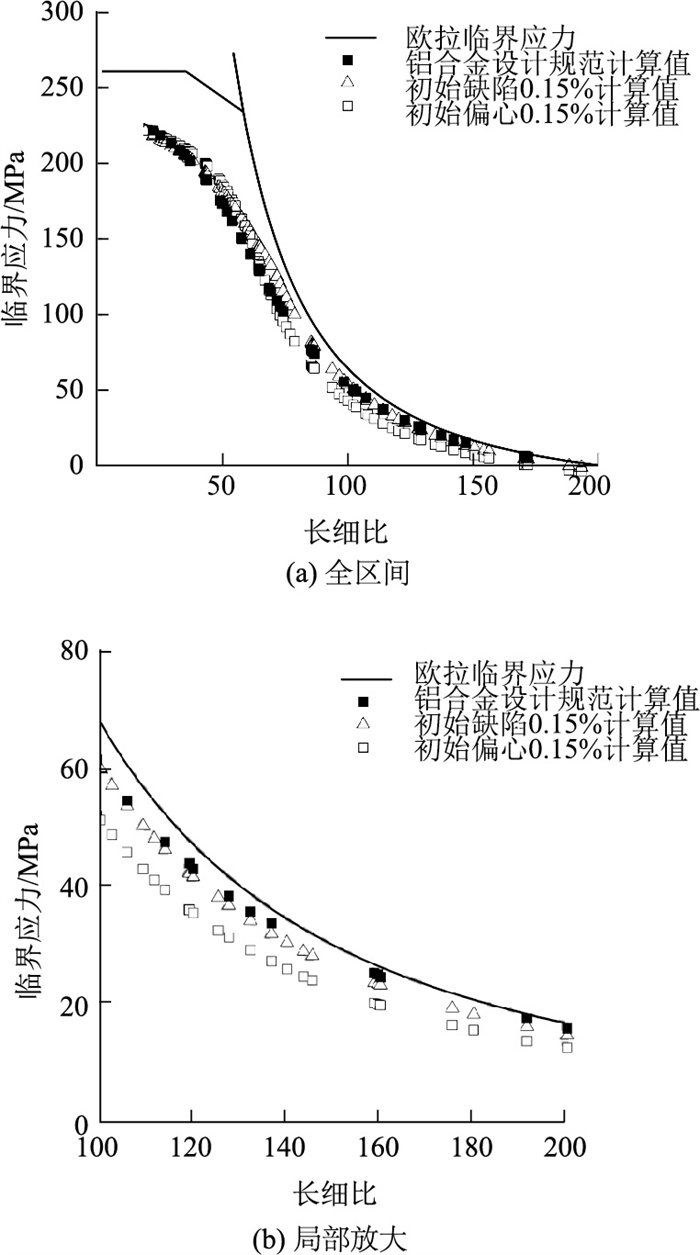
|
| 图 8 轴心受压稳定承载力对比 Fig. 8 Comparison of stability bearing capacity under axial load |
| |
| 初始偏心/% | 长细比 | 比例 |
| 0.05 | >59.28 | 0.742 |
| 0.10 | >59.28 | 0.678 |
| 0.15 | >59.28 | 0.621 |
| 0.20 | >59.28 | 0.571 |
| 0.25 | >59.28 | 0.528 |
5 与现行规范的比较 5.1 比较对象
GB 50429—2007对轴心受压杆件的稳定系数取值为:
| $ \varphi=\frac{1}{2 \bar{\lambda}^2}\left\{\left(1+\eta+\bar{\lambda}^2\right)-\left[\left(1+\eta+\bar{\lambda}^2\right)^2-4 \bar{\lambda}^2\right]^{\frac{1}{2}}\right\}, $ | (10) |
式中,φ为按照公式计算所得的稳定系数;λ为正则化长细比,λ =(λ/π)
按照式(10)可计算出规范规定下不考虑局部屈曲的轴心构件受压承载力。规范计算数据、迭代法计算数据因为考虑了抗力分项系数,取材料强度设计值为200 MPa。在单考虑材料性能的情况下比较时,将计算所得临界应力乘以抗力分项系数,得到它们在比例极限240 MPa下的承载力。依照相关规范限制值[10],取对比杆件的初始弯曲为0.15%;在试验研究[4]中测得初始偏心多位于0.15%附近,该值具有代表性,因此取初始弯曲为0.15%的杆件临界应力、初始偏心为0.15%的杆件临界应力与现行规范值所计算的临界应力进行比较,并将三者所有的数据转化为临界应力与长细比。
5.2 结果分析欧拉临界应力曲线、规范计算值、0.15%初始弯曲计算值、0.15%初始偏心计算值的比较情况如图 8所示[18]。从总体上看,规范计算值与初始弯曲、初始偏心下迭代法计算值较为接近,三者变化趋势相同,在全区间内计算值均小于欧拉临界应力总图的曲线。
长细比小于30时,由于规范计算值考虑了局部屈曲,而本研究未考虑这一部分,因此规范计算值偏安全;长细比为30~95时,初始弯曲为0.15%的杆件临界应力、初始偏心为0.15%的杆件临界应力与现行规范值所计算的临界应力计算结果相近,未出现规范值均大于二者的情况,规范值比较安全;长细比大于95后,规范计算所得临界应力比初始弯曲为0.15%的杆件临界应力与初始偏心为0.15%的杆件的临界应力大,且随着长细比的增大,这一差值也会逐渐增大;长细比为200时,规范值比杆件0.15%初始弯曲下计算值偏大7.50%,比杆件0.15%初始偏心计算值偏大25.72%,此时构件会出现过大的横向挠度,已不满足正常使用的要求。规范未综合限制杆件承载力计算中的横向挠度,此部分本研究计算方法偏安全。
同时注意到在长细比较大的阶段,初始偏心计算值较初始弯曲计算值、规范计算值偏差较大。这说明初始偏心对承载力影响较大,应对其严格限制。
6 结论随着铝合金材料在桥梁结构中的应用不断增加,结构安全成为工程关注的重要目标,其中受压杆件的稳定性成为制约设计的关键性因素。通过采用ABAQUS软件与迭代程序对多种截面、长度的铝合金轴心受压杆件进行分析,并开展参数化研究,同时与现行规范进行对比。
(1) 得出了在4种初始弯曲影响下杆件临界应力与欧拉临界应力比值的3个阶段及其分值点,给出了此比值曲线3个阶段的拟合公式。此公式适用于具有不同初始弯曲的轴压杆件安全承载力计算。
(2) 得出了在6种初始偏心影响下杆件临界应力与欧拉临界应力比值的2个阶段及其分值点,给出了此比值曲线2个阶段的拟合公式。此公式适用于由安装误差造成具有不同小初始荷载偏心的轴压杆件安全承载力计算。
(3) 相对于在常见初始缺陷下的计算值而言,长细比较小的情况下,规范计算值考虑了局部屈曲,偏安全;长细比较大的情况下,杆件都是因为横向挠度较大失效,规范未加考虑,因此本研究计算方法偏安全。
(4) 初始偏心对承载力影响较大,应对其严格限制。长细杆件的极限承载力多由挠度控制,实际工程中应对其进行监控。
| [1] |
曹少成, 闫亚杰, 武启宇, 等. 铝合金网壳中不锈钢螺栓连接的抗剪性能研究与应用[J]. 太原理工大学学报, 2022, 53(2): 315-322. CAO Shaocheng, YAN Yajie, WU Qiyu, et al. Research and application of shear resistance of stainless steel bolted connection in aluminum alloy reticulated shell[J]. Journal of Taiyuan University of Technology, 2022, 53(2): 315-322. |
| [2] |
徐业飞. 铝合金人行天桥结构分析[D]. 杭州: 浙江大学, 2007. XU Yefei. Structural analysis of aluminum alloy pedestrian overpass[D]. Hangzhou: Zhejiang University, 2007. |
| [3] |
王元清, 常婷, 石永久, 等. 铝合金轴心受压构件局部整体相关稳定试验研究[J]. 土木工程学报, 2016, 49(1): 14-22. WANG Yuanqing, CHANG Ting, SHI Yongjiu, et al. Experimental study on local-overall interactive buckling behaviors of aluminum alloy columns under axial compression[J]. China Civil Engineering Journal, 2016, 49(1): 14-22. |
| [4] |
翟希梅, 吴海, 王誉瑾, 等. 铝合金轴心受压构件的稳定性研究与数值模拟[J]. 哈尔滨工业大学学报, 2011, 43(12): 1-6. ZHAI Ximei, WU Hai, WANG Yujin, et al. Stability research and numerical simulation of high-strength aluminum alloy column in compression[J]. Journal of Harbin Institute of Technology, 2011, 43(12): 1-6. |
| [5] |
黄海林, 何培根, 周福林, 等. 粘铝合金板加固RC梁抗弯性能试验及正截面承载力[J]. 公路交通科技, 2024, 41(1): 105-115, 125. HUANG Hailin, HE Peigen, ZHOU Fulin, et al. Flexural behavior test and normal section bearing capacity of RC beam strengthened with aluminum alloy plate[J]. Journal of Highway and Transportation Research and Development, 2024, 41(1): 105-115, 125. DOI:10.3969/j.issn.1002-0268.2024.01.013 |
| [6] |
原国森, 杨占尧. 热挤压对粉末冶金6061铝合金显微组织和抗拉强度的影响[J]. 机械工程材料, 2018, 42(1): 68-71. YUAN Guosen, YANG Zhanyao. Effect of hot extrusion on microstructure and tensile strength of powder metallurgy 6061 aluminum alloy[J]. Materials for Mechanical Engineering, 2018, 42(1): 68-71. |
| [7] |
班慧勇. 高强度钢材轴心受压构件整体稳定性能与设计方法研究[D]. 北京: 清华大学, 2012. BAN Huiyong. Research on the overall buckling behavior and design method of high strength steel columns under axial compression[D]. Beijing: Tsinghua University, 2012. |
| [8] |
张景桥, 兰巍, 申昊, 等. 铰接和刚接模型对钢桁梁设计的影响[J]. 水运工程, 2011(增1): 35-38. ZHANG Jingqiao, LAN Wei, SHEN Hao, et al. Influence of hinged and consolidated models on steel truss design[J]. Port & Waterway Engineering, 2011(S1): 35-38. |
| [9] |
RASMUSSEN K J R, HANCOCK G J. Tests of high strength steel columns[J].
Journal of Constructional Steel Research, 1995, 34(1): 27-52.
DOI:10.1016/0143-974X(95)97296-A |
| [10] |
曹少成. 不锈钢螺栓连接下铝合金网壳结构板式节点的静力性能研究[D]. 太原: 太原理工大学, 2022. CAO Shaocheng. Study on static performance of plate joints of aluminum alloy reticulated shell structure with stainless steel bolt connection[D]. Taiyuan: Taiyuan University of Technology, 2022. |
| [11] |
庄茁, 张帆, 岺松. ABAQUS非线性有限元分析与实例[M]. 北京: 科学出版社, 2005. ZHUANG Zhuo, ZHANG Fan, CEN Song. ABAQUS nonlinear finite element analysis and examples[M]. Beijing: China Science Publishing, 2005. |
| [12] |
王誉瑾. 6082\|T6铝合金轴心受压构件稳定性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. WANG Yujin. Investigation on the stability of aluminum alloy 6082\|T6 members in axial compression[D]. Harbin: Harbin Institute of Technology, 2015. |
| [13] |
陈丽晖. 高强度铝合金构件弹塑性稳定性分析[D]. 长春: 吉林大学, 2022. CHEN Lihui. Elastoplastic stability analysis of high strength aluminum alloy members[D]. Changchun: Jilin University, 2022. |
| [14] |
王欢, 康玲, 牟廷敏, 等. 空间异形桥塔的稳定极限承载力计算方法[J]. 公路交通科技, 2024, 41(4): 110-119. WANG Huan, KANG Ling, MU Tingmin, et al. Calculation method for stable ultimate bearing capacity of irregular space-shaped bridge pylon[J]. Journal of Highway and Transportation Research and Development, 2024, 41(4): 110-119. DOI:10.3969/j.issn.1002-0268.2024.04.012 |
| [15] |
张涛然, 晁晓洁, 郭丽红. 材料力学[M]. 重庆: 重庆大学出版社, 2018. ZHANG Taoran, CHAO Xiaojie, GUO Lihong. Mechanics of materials[M]. Chongqing: Chongqing University Press, 2018. |
| [16] |
云磊. 牛顿迭代法的MATLAB实现[J]. 信息通信, 2011(6): 20-21. YUN Lei. MATLAB implementation of Newton iteration method[J]. Information & Communications, 2011(6): 20-21. |
| [17] |
游勇, 蒋习伟. 求解纯弯曲梁挠曲线问题的讨论[J]. 湖南科技学院学报, 2009, 30(8): 29-30. YOU Yong, JIANG Xiwei. Discussion on solving deflection curve of pure bending beam[J]. Journal of Hunan University of Science and Technology, 2009, 30(8): 29-30. |
| [18] |
郭小农, 沈祖炎, 李元齐, 等. 铝合金轴心受压构件理论和试验研究[J]. 建筑结构学报, 2007, 28(6): 118-128. GUO Xiaonong, SHEN Zuyan, LI Yuanqi, et al. Theoretical and experimental research on aluminum alloy members under axial compression[J]. Journal of Building Structures, 2007, 28(6): 118-128. |
 2025, Vol. 42
2025, Vol. 42



 ,
,