扩展功能
文章信息
- 许红胜, 杨盈, 颜东煌, 曾懿, 赵明富, 邹飘.
- XU Hongsheng, YANG Ying, YAN Donghuang, ZENG Yi, ZHAO Mingfu, ZOU Piao
- 高强钢丝双裂纹屏蔽效应的疲劳试验研究
- Experimental study on fatigue performance of high strength steel wire double cracks shielding effect
- 公路交通科技, 2025, 42(6): 123-132
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(6): 123-132
- 10.3969/j.issn.1002-0268.2025.06.013
-
文章历史
- 收稿日期: 2023-06-20
2. 贵州省公路工程集团有限公司, 贵州 贵阳 550008
2. Guizhou Highway Engineering Group Co., Ltd., Guiyang, Guizhou 550008, China
经过多年对交通基础设施建设的持续投入,中国已建成的索支承桥梁数量居于国际前列。作为索支承桥梁的关键受力构件,索构件的使用寿命直接与内部钢丝的腐蚀情况相关[1-3]。锈蚀坑是钢丝表面腐蚀损伤的常见形式,钢丝的疲劳应力幅和蚀坑会导致钢丝表面裂纹形成和加速扩展并引起断裂,从而对拉索钢丝的运营安全构成重大威胁[4-6]。尽管有一些研究为腐蚀拉索钢丝静态强度评估提供了参考[7],但仍缺乏对具有复杂腐蚀坑分布的劣化钢丝疲劳性能的有效试验和理论研究,故难以对腐蚀拉索的剩余疲劳寿命进行精细化评估。
关于金属部件腐蚀疲劳寿命预测的研究,不少学者提出将腐蚀缺陷假设为表面上初始裂纹的等效初始缺陷尺寸, 来预测腐蚀金属结构的疲劳寿命,且认为等效初始缺陷尺寸方法是在疲劳设计中定量评估腐蚀损伤的有效假设[8-11]。多个针对腐蚀钢丝的疲劳试验测试均显示,疲劳微裂纹萌生于钢丝点蚀坑并发展形成长裂纹[12-13],且由于对蚀坑形状尺寸无法准确定量,大部分研究通过等效缺陷尺寸方法对腐蚀钢丝的疲劳行为进行分析和评估。Jiang[14]采用预制裂纹的高强度镀锌钢丝来模拟钢丝腐蚀疲劳行为,进行了不同应力比下的疲劳试验研究。Jiang[15]对桥梁用高强度腐蚀钢丝的疲劳性能进行了试验研究,通过对腐蚀丝试件的形貌表征和疲劳性能分析,假定腐蚀坑最大深度处为半椭圆表面裂纹,并利用AFGROW软件和三维测量技术,提出了一种腐蚀钢丝剩余疲劳寿命的预测方法。Wang[16]基于3D扫描技术提出了蚀坑深度与腐蚀程度的定量关系,并基于等效初始裂纹尺寸评估锈蚀钢丝的疲劳寿命。郑祥隆[17]总结了不同屈服强度和应力比下钢丝裂纹扩展的经验模型,并运用到基于等效裂纹假定的预腐蚀钢丝疲劳寿命预测方法中,发现钢丝裂纹扩展经验模型和等效初始裂纹深度的假定能够更好地模拟腐蚀钢丝的疲劳特性。
对腐蚀钢丝表面蚀坑形态及分布的研究表明,腐蚀钢丝的表面点蚀坑分布位置和蚀坑形态具有典型的随机特性[3, 12]。因此较合理的腐蚀钢丝剩余疲劳寿命评估理论研究需要考虑随机分布的相邻点蚀坑的相互影响问题。Miao[18]预制具有不同特征参数双凹坑的钢丝,通过疲劳试验研究了凹坑深度、宽度、位置和应力振幅对钢丝疲劳寿命的影响。结果表明双凹坑的叠加作用会稍微延长钢丝的疲劳寿命。Ye[19]基于将半个椭圆形裂纹代替实际蚀坑的简化规则,系统地研究了轴向载荷下钢丝中双共面半椭圆表面裂纹的形状扩展和相互作用效应。张洪[20]获取了旧钢绞线拉索的钢丝腐蚀图像,针对腐蚀钢丝的疲劳试验表明,腐蚀程度的加深(多个凹坑)会大幅降低钢丝的疲劳寿命。叶华文[21]以不同缺口形状模拟单蚀坑和双蚀坑,同时基于临界域法预测钢丝疲劳寿命。
从国内外多裂纹构件疲劳寿命的相关理论研究来看,2条相同且平行的微裂纹周围的空间可以分为所谓的“增强”区域和“屏蔽”区域。“屏蔽”指的是裂纹尖端应力强度因子被削弱,即正屏蔽效应,“增强”为负屏蔽效应;多裂纹对应力强度因子的屏蔽或增强效应会导致多裂纹构件的疲劳寿命与单裂纹构件有明显差异[22-24]。由于拉索钢丝的结构形态特异性,针对平板的多裂纹屏蔽效应的研究成果不能完全有效适用腐蚀钢丝[25],故有必要针对拉索腐蚀钢丝进行系统的多裂纹屏蔽效应的相关试验和理论研究。
本研究在将高强钢丝的相邻点蚀坑假设为双长裂纹的基础上,结合高强钢丝双裂纹应力场相互影响的理论分析研究成果,考虑双裂纹在高强钢丝中的不同位置分布和双裂纹的尺寸差异变化,进行了预制双裂纹的高强钢丝疲劳试验研究。探讨了高强钢丝双裂纹屏蔽效应的试验规律,并将疲劳仿真分析软件给出的计算结果与试验结果进行了比较。
1 疲劳试验设计 1.1 试件取材桥梁索结构的内部钢丝常采用直径为5~7 mm的高强度钢丝。为了保证试验钢丝试件的代表性,本研究采用曾用于2010年建成实桥,并于2021年拆解的旧拉索内部未锈蚀钢丝(直径为7 mm的1 670 MPa级别高强钢丝)作为试验测试试件。选取材料时确定钢丝表面光滑,无明显腐蚀和缺陷,尽量减少钢丝试件材料初始缺陷的影响。
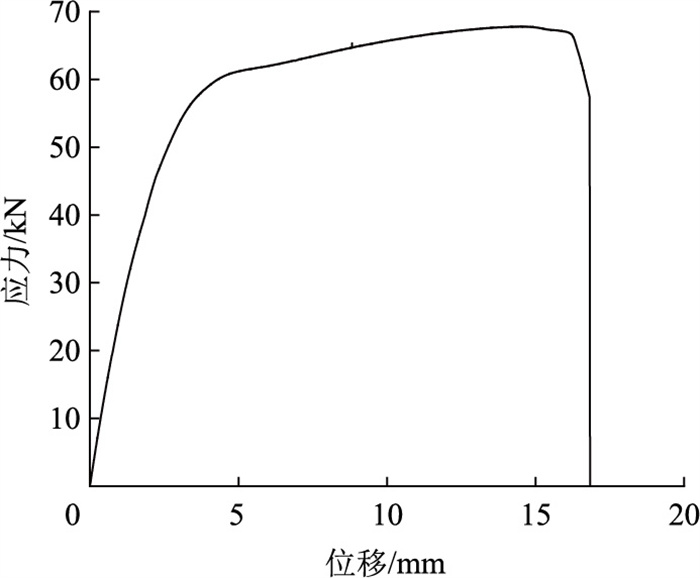
为了检验该高强钢丝材料静力承载能力和性能的情况,依据规范《桥梁缆索用热镀锌钢丝》(GT/T 17101—2019)取部分钢丝试件进行了拉伸试验和疲劳试验,钢丝试样拉伸试验的力-位移曲线如图 1所示,高强度钢丝试件力学指标测试值如表 1所示。无预制裂纹的钢丝试件360 MPa应力下加载200万次未断裂,这说明选取的钢丝试件剩余疲劳寿命满足规范要求。
|
| 图 1 钢丝试样拉伸试验的力 Fig. 1 Force-displacement curve of steel wire specimen for tensile test |
| |
| 力学指标 | 弹性模量/ (×105 MPa) | 抗拉强度/ MPa | 断面收缩率/ % | 断后伸长率/ % |
| 测试值 | 2.01 | 1 704.56 | 30.82 | 4.32 |
| 规范值 | 2.0±0.1 | ≤1 870.0 | ≥30.0 | ≥4.0 |
1.2 试件制备
根据拉索所处的实际环境和受力情况,在疲劳载荷作用下,高强度钢丝点蚀坑会产生应力集中,进而导致裂纹从点蚀坑中迅速萌生。自然萌生的钢丝表面裂纹一般呈现为半椭圆形[26-28]。故许多学者提出将蚀坑简化为半椭圆形平面裂纹来进行研究,并取得了有效性结论[11, 17, 29]。本研究将蚀坑简化为半椭圆平面裂纹,以平面裂纹长短轴等效蚀坑宽度与深度。考虑到实际腐蚀钢丝中点蚀坑随机分布的特性,本研究侧重于研究2个临近的平面裂纹在位置和大小不同的情况下,其间的相互作用对钢丝疲劳寿命的影响。
可将根据锈蚀程度估算的蚀坑深度假定为初始裂纹深度,能较好地模拟腐蚀钢丝恒幅疲劳试验的结果[17],进一步依据锈蚀率和累积概率确定了严重腐蚀钢丝的最大蚀坑深度约为0.6 mm。通过对钢丝上腐蚀坑形状和大小的研究发现[18],深度0.2~0.6 mm蚀坑对疲劳寿命影响较大。故本研究将蚀坑深度0.6 mm假定为试件主裂纹特征参数,取蚀坑深度0.2,0.4,0.6 mm作为从裂纹特征参数;经过对多种预制裂纹加工技术的比选,最终采用不会破坏钢丝材料特性的机床铣削加工方法。
试验采用的钢丝试样直径和长度分别为7 mm和410 mm,预先对钢丝试样加工出不同深度和分布的预制表面主、从裂纹,预制裂纹垂直于钢丝试样轴线分布于试样中段。试件预制裂纹设计如图 2所示。图中C1为主裂纹,C2为从裂纹;d为同轴平行双裂纹试样的主、从裂纹间的轴向间距;b为单裂纹试样的主裂纹长度,b1为双裂纹试样的主裂纹长度,b2为双裂纹试样的从裂纹长度;H为单裂纹试样的主裂纹深度,H1为双裂纹试样的主裂纹深度,H2为双裂纹试样的从裂纹深度;θ为同轴共面双裂纹试样的主、从裂纹间的周向夹角。

|
| 图 2 试件预制裂纹设计(单位:mm) Fig. 2 Prefabricated cracks design for specimen (unit: mm) |
| |
1.3 试验加载设计
疲劳试验加载设备为MTS电子万能试验机,采用载荷控制,按正弦波加载。根据相关文献[30]的研究结果,试验频率在10~64 Hz范围内对于试验结果并无显著影响;结合加载设备的实操性,采取循环加载频率为6 Hz。每个钢丝试样布置一个应变片,位于主裂纹上部80 mm的位置,同步利用动态应变测试仪进行加载应力幅的监测。疲劳试验加载方案参照标准(GB/T 17101—2019)要求,考虑缆索钢丝使用中容许应力小于0.5倍的抗拉强度,参照文献[31]的实际拉索工作应力幅的分析结果,偏安全取钢丝试样的最大加载应力值为420 MPa。同时结合加载设备的荷载控制条件,确定应力级差为30 MPa,则试验设计加载应力幅(ΔS)可取390,360,330 MPa。
2 试验结果与数据分析本研究试验设置分为A,B,C组,如表 2所示。其中A组为1#的单裂纹钢丝试样疲劳试验,B组为2#~10#的同轴平行双裂纹钢丝试样疲劳试验,C组为11#~16#的同轴共面双裂纹钢丝试样批量试验。A组24根试件,分为2类裂纹深度、4种应力幅,每种3根钢丝试件;B组中,每种编号12根试件,分为4种应力幅,每种3根钢丝试件;C组中,每种编号12根试件,分为4种应力幅,每种3根钢丝试件。为了研究裂纹深度、裂纹间的相对位置和加载应力幅值的变化对双裂纹钢丝试件疲劳寿命的屏蔽效应,需要选取单裂纹钢丝试样作为对照组,所以先期进行单裂纹钢丝试样的疲劳试验。本研究中,各钢丝试样组的疲劳寿命取3根钢丝试样的平均寿命。
| 组别 | 裂纹类型 | 编号 | 平面裂纹尺寸的控制参数数值/mm | 周向角度θ/(°) |
| A | 单裂纹 | 1# | H=0.6,b=2.84 H=0.4,b=2.34 |
|
| B | 平行双裂纹 | 2# | H1=0.6,b1=2.84,H2=0.6,b2=2.84,d=0.5 | 0° |
| 3# | H1=0.6,b1=2.84,H2=0.6,b2=2.84,d=1.0 | 0° | ||
| 4# | H1=0.6,b1=2.84,H2=0.6,b2=2.84,d=1.5 | 0° | ||
| 5# | H1=0.6,b1=2.84,H2=0.4,b2=2.34,d=0.5 | 0° | ||
| 6# | H1=0.6,b1=2.84,H2=0.4,b2=2.34,d=1.0 | 0° | ||
| 7# | H1=0.6,b1=2.84,H2=0.4,b2=2.34,d=1.5 | 0° | ||
| 8# | H1=0.6,b1=2.84,H2=0.2,b2=1.66,d=0.5 | 0° | ||
| 9# | H1=0.6,b1=2.84,H2=0.2,b2=1.66,d=1.0 | 0° | ||
| 10# | H1=0.6,b1=2.84,H2=0.2,b2=1.66,d=1.5 | 0° | ||
| C | 共线双裂纹 | 11# | H1=0.6,b1=2.84,H2=0.6,b2=2.84,d=0 | 90° |
| 12# | H1=0.6,b1=2.84,H2=0.6,b2=2.84,d=0 | 180° | ||
| 13# | H1=0.6,b1=2.84,H2=0.4,b2=2.34,d=0 | 90° | ||
| 14# | H1=0.6,b1=2.84,H2=0.4,b2=2.34,d=0 | 180° | ||
| 15# | H1=0.6,b1=2.84,H2=0.2,b2=1.66,d=0 | 90° | ||
| 16# | H1=0.6,b1=2.84,H2=0.2,b2=1.66,d=0 | 180° |
2.1 裂纹深度对单裂纹疲劳寿命影响分析
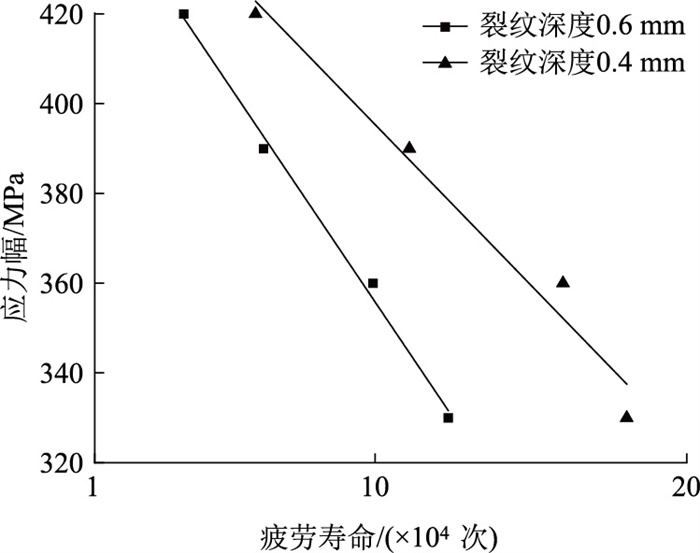
单裂纹钢丝试样的加载应力幅-疲劳寿命曲线如图 3所示。由图可见,不同裂纹深度单裂纹钢丝试件的加载应力幅-疲劳寿命(以下简写为ΔS-N) 曲线具有明显的规律性。随着裂纹深度和应力幅的增加,单裂纹钢丝试件的疲劳寿命快速下降,同时,不同裂纹深度单裂纹钢丝试件的ΔS-N曲线斜率存在明显差异。这表明随着裂纹深度的增加,疲劳裂纹扩展速率有明显的增加,会使疲劳寿命降低数倍甚至10倍,因此应注意高应力幅值钢丝的腐蚀和长裂纹的扩展。
|
| 图 3 单裂纹钢丝试样的加载应力幅-疲劳寿命曲线 Fig. 3 Curves of loading stress amplitude and fatigue life of single-crack steel wire |
| |
2.2 同轴平行双裂纹屏蔽效应分析
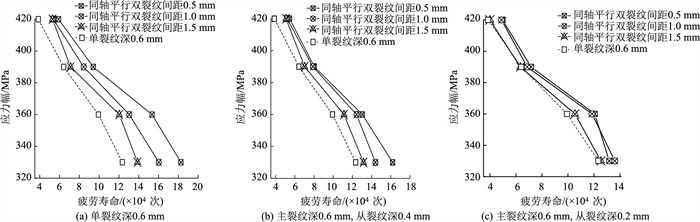
不同主-从裂纹深度及不同裂纹间距的同轴平行双裂纹钢丝试样的加载应力幅-疲劳寿命曲线如图 4所示。由图可见,同轴平行双裂纹钢丝试件的疲劳寿命均高于单裂纹钢丝试件疲劳寿命,这表现出明显的正屏蔽效应;双裂纹间的正屏蔽效应随双裂纹轴向间距的减小而增强,随双裂纹轴向间距的增大而减弱。同轴平行双裂纹钢丝试样比单裂纹钢丝试样疲劳寿命的增加比例如表 3所示。可以看出从裂纹深度越大,双裂纹间的屏蔽效应越显著;从裂纹深度大于0.2 mm,主-从裂纹间轴向间距较小时,仍存在明显的屏蔽效应;同时,当双裂纹轴向间距大于3倍主裂纹深度时,屏蔽效应也相对不明显。
|
| 图 4 不同裂纹间距的同轴平行双裂纹钢丝试样的加载应力幅-疲劳寿命曲线 Fig. 4 Curves of loading stress amplitude and fatigue life of coaxial parallel double cracks with different crack spacings |
| |
| 同轴平行双裂纹间距/mm | 不同深度(mm)主-从裂纹疲劳寿命增加比例/% | ||
| 0.6 | 主0.6,从0.4 | 主0.6,从0.2 | |
| 0.5 | 100 | 50 | 15 |
| 1.0 | 50 | 25 | 10 |
| 1.5 | 20 | 10 | 3 |
2.3 同轴共面双裂纹屏蔽效应分析
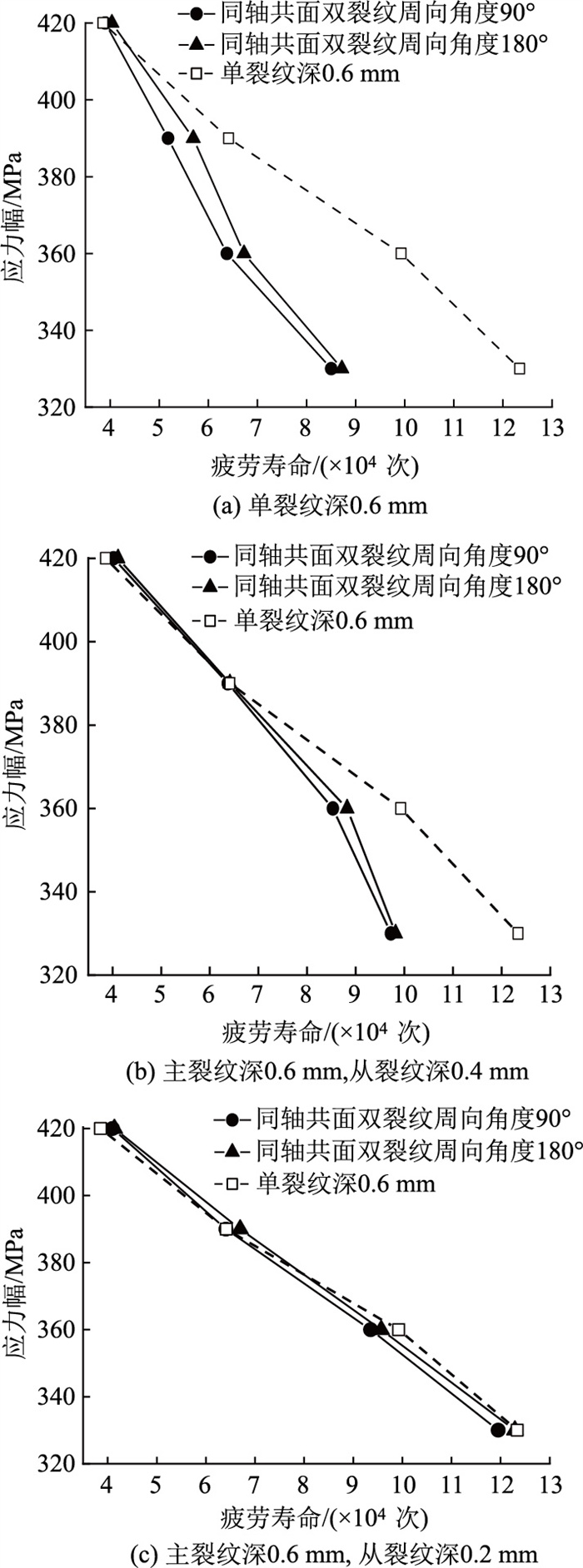
不同主-从裂纹深度及不同周向角度的同轴共面双裂纹的加载应力幅-疲劳寿命曲线如图 5所示。由图可见,对于同轴共面双裂纹钢丝试件,当主-从裂纹尺寸接近时,双裂纹试样疲劳寿命明显低于单裂纹试样,表现出明显的负屏蔽效应;主-从裂纹尺寸越接近,双裂纹间的负屏蔽效应随双裂纹轴向夹角的减小而增强的趋势越明显;当主-从裂纹尺寸相差较大时,双裂纹间负屏蔽效应与双裂纹轴向夹角的关联性相对减弱。同轴共面双裂纹钢丝试样比单裂纹钢丝试样的疲劳寿命减小比例如表 4所示,可以看出从裂纹深度越大,双裂纹间的负屏蔽效应越显著。当从裂纹深度小于0.2 mm时,双裂纹试样疲劳寿命与单裂纹试样基本相同,从裂纹对主裂纹的疲劳寿命已基本无影响。
|
| 图 5 不同周向角度的同轴共面双裂纹的加载应力幅- 疲劳寿命曲线 Fig. 5 Curves of loading amplitude and fatigue life of coaxial coplanar double cracks with different circumferential angles |
| |
| 周向角度/ (°) | 不同深度(mm)主-从裂纹疲劳寿命减小比例/% | ||
| 0.6 | 主0.6,从0.4 | 主0.6,从0.2 | |
| 90 | 30 | 15 | 5 |
| 180 | 25 | 11 | 3 |
3 数值模拟分析 3.1 有限元分析模型的建立
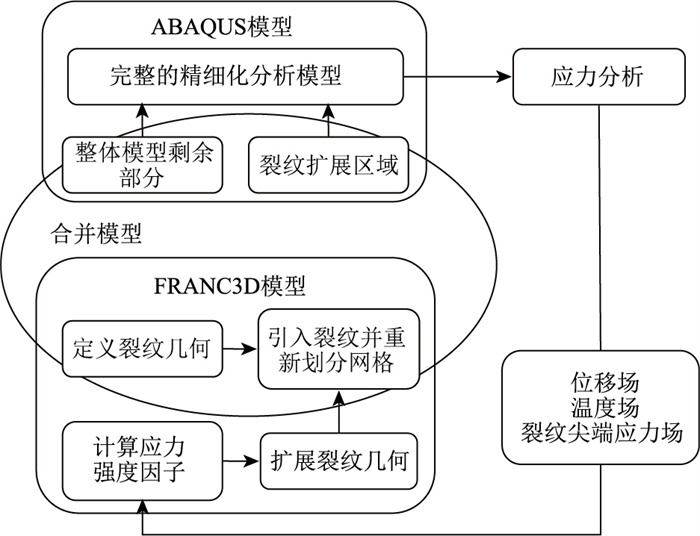
带裂纹构件疲劳寿命的仿真计算方法多面向单裂纹构件,对多裂纹钢丝疲劳寿命的计算方法还缺乏系统研究。本研究采用FRANC3D和ABAQUS联合仿真计算方法,对带初始预制双裂纹的钢丝试件进行疲劳裂纹扩展寿命的预测分析。双裂纹钢丝试样疲劳裂纹扩展模拟联合仿真计算分析流程如图 6所示。本研究给出的联合仿真计算方法的特点为:结合了ABAQUS软件对多裂纹钢丝应力应变场和应力强度因子计算的可靠性和FRANC3D对含裂纹钢丝裂纹扩展模拟的精确性;将FRANC3D带裂纹细化局部模型导入ABAQUS整体模型中,整合得到合并模型;实现了ABAQUS模型与FRANC3D模型间的有效数据交换和分析传递;解决了ABAQUS软件疲劳寿命评估中对ΔS-N曲线的依赖问题和FRANC3D软件自身无法准确计算应力强度因子的问题。
|
| 图 6 疲劳裂纹扩展模拟流程 Fig. 6 Fatigue crack propagation simulation flow |
| |
在ABAQUS模型建立时,钢丝试样的长度为260 mm,直径为7 mm;预制裂纹建模形状为椭圆形,长半轴为
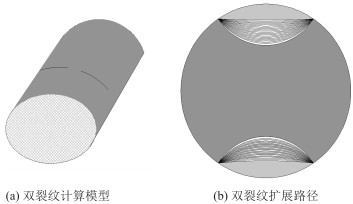
进行FRANC3D裂纹扩展分析时,裂纹扩展步从0~15分为15个扩展分析步,计算扩展路径如图 7所示。钢丝疲劳裂纹扩展性能的基本参数C=4.63e-11,m=1.993;断裂韧性KIC=65.7
|
| 图 7 双裂纹计算模型及扩展路径 Fig. 7 Calculation model and expansion path for double cracks |
| |
3.2 仿真计算与试验疲劳寿命结果比较
利用3.1节联合仿真计算分析方法,计算得到与试验同等条件下16组钢丝的剩余疲劳寿命。通过比较试验下和数值模拟的双裂纹钢丝疲劳寿命二者的数据,评估FRANC3D和ABAQUS联合仿真能否较好地模拟分析双裂纹钢丝疲劳寿命。为了直观地对比理论计算与试验结果的差异,定义偏差系数j。
| $ j=\frac{(\text { 试验值 }- \text { 数值模拟值 })}{\text { 数值模拟值 }} \times 100 \% \text { 。} $ | (1) |
(1) 单裂纹数值模拟比较
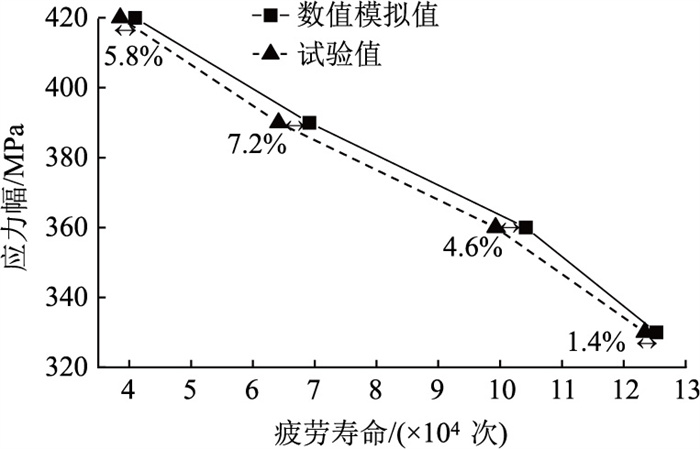
深度0.6 mm单裂纹试验结果与数值计算结果的对比如图 8所示。由图可见,FRANC3D和ABAQUS联合数值仿真模拟的预测寿命与试验结果的最大误差仅为7.2%,且预测值均大于试验值。这说明采用FRANC3D计算的单裂纹钢丝预测疲劳寿命具有良好的拟合度,可以作为单裂纹高强钢丝试验疲劳寿命评估的依据。
|
| 图 8 单裂纹试验结果与数值计算结果对比 Fig. 8 Single crack test result v.s. numerical simulation result |
| |
(2) 同轴平行双裂纹数值模拟比较
同轴平行双裂纹钢丝试样的疲劳寿命试验结果与数值模拟结果的对比如图 9所示。由图可见,随着试验加载应力幅的增大,仿真预测值与试验值的误差存在增大趋势。应力幅较小时,仿真预测值与试验值吻合度较好。不同裂纹间距情况下同轴平行双裂纹试验值与数值模拟值最大偏差比例如表 5所示,可以看出同轴平行双裂纹的从裂纹深度和裂纹轴向间距变化对仿真预测值的准确性无明显影响规律。

|
| 图 9 同轴平行双裂纹疲劳寿命试验结果与数值模拟结果对比 Fig. 9 Coaxial parallel double cracks fatigue life test results v.s. numerical simulation results |
| |
| 同轴平行双裂纹间距/mm | 不同深度(mm)主、从裂纹的同轴平行双裂纹的最大偏差/% | ||
| 0.6 | 主0.6,从0.4 | 主0.6,从0.2 | |
| 0.5 | 32.5 | 30.0 | 29.6 |
| 1.0 | 37.7 | 32.2 | 23.2 |
| 1.5 | 33.9 | 25.2 | 27.0 |
(3) 同轴共面双裂纹数值模拟比较
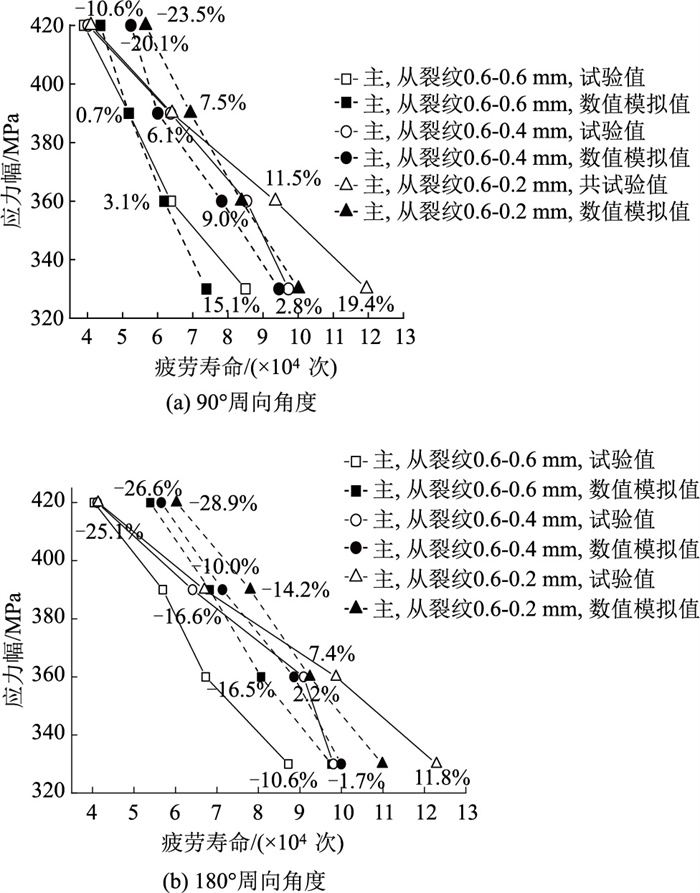
同轴共面双裂纹疲劳钢丝试样的疲劳寿命试验结果与数值模拟结果对比如图 10所示。由图可见,试验结果与数字模拟结果的差异与试验加载应力幅无明显关联性;仿真预测值部分低于试验值,部分高于试验值,无显著规律。这表明数值仿真方法难以有效精确评估同轴共面双裂纹间负屏蔽效应的影响。不同周向角度下同轴共线双裂纹钢丝试样试验值与数值模拟值最大偏差比例如表 6所示。可以看出同轴共面双裂纹的从裂纹深度和裂纹周向角度变化对仿真预测值的准确性无明显影响。
|
| 图 10 同轴共面双裂纹疲劳寿命试验结果与数值模拟结果对比 Fig. 10 Coaxial coplanar double cracks fatigue life test results v.s. numerical simulation results |
| |
| 周向角度/ (°) | 不同深度(mm)主、从裂纹的同轴共线双裂纹的最大偏差/% | ||
| 0.6 | 主0.6,从0.4 | 主0.6,从0.2 | |
| 90 | 15.1 | ―20.1 | ―23.5 |
| 180 | ―25.1 | ―26.6 | ―28.9 |
3.3 计算结果偏差分析
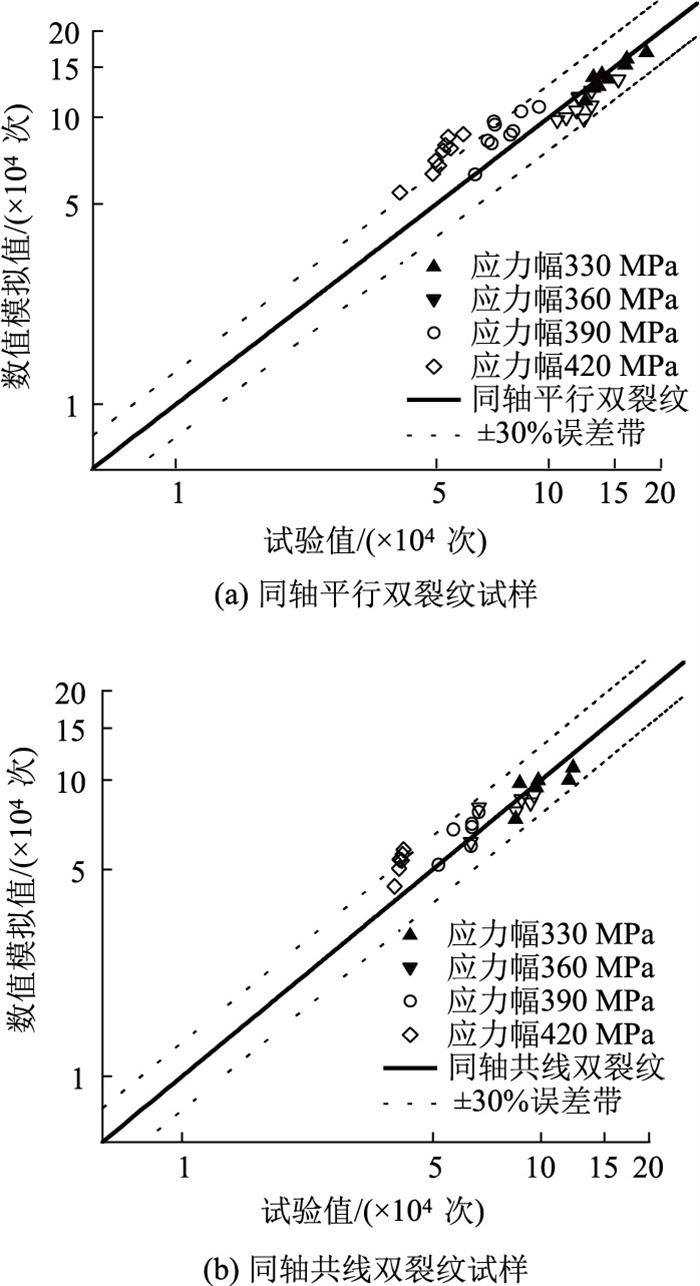
双裂纹钢丝试样的疲劳寿命模拟值与试验值的误差分布如图 11所示。图中x轴表示钢丝试验疲劳寿命,y轴表示所采用的数值模拟预测疲劳寿命。由图可见,2种模型预测的疲劳寿命随着应力范围的减小而趋近于试验值。在低应力范围下(ΔS≤360 MPa),2种双裂纹的数值模拟预测寿命与试验结果相对误差较小,且较为均匀地分布在对角线两侧;但对于在高应力范围下(ΔS >360 MPa)的平行双裂纹试样,数值模拟计算出来的疲劳寿命与试验数据之间存在较大偏差。误差出现的主要原因是所提出的疲劳寿命数值模拟模型未考虑预制缺口三维深宽比的影响,直接将缺口等效成二维初始裂纹尺寸。
|
| 图 11 疲劳寿命模拟值与试验值对比 Fig. 11 Fatigue life simulation values v.s. experimental values |
| |
此外,偏差原因也源于FRANC3D软件对于主-从裂纹扩展采用等比例扩展的假定,即从裂纹的扩展尺寸由主裂纹扩展决定,这与实际情况存在显著差异。当应力幅较大时,这种偏差导致的影响也可能较大。总体来说,数值模拟值与试验值存在偏差的原因在于实际预制裂纹及裂纹扩展情况与数值仿真模拟情况均存在明显的不同。
虽然在高应力幅下数值模拟值与试验值有一定的偏差,但平行双裂纹试样和共线双裂纹试样有超过95%的预测值仍然落在±30%误差带内(图 11中虚线所示)。在工程应用中,较好的偏差范围为±15%。整体来看,对比Liu[13]的预测值与试验值所取的±2倍误差带,利用FRANC3D和ABAQUS对钢丝疲劳寿命进行模拟具有较好的适用性。
4 结论本研究进行了预制双裂纹钢丝试样的疲劳试验和疲劳寿命数值仿真计算研究,主要结论如下。
(1) 同轴平行双裂纹钢丝试样的疲劳寿命要高于单裂纹钢丝试样,同轴平行双裂纹间的间距减小和从裂纹尺寸增大会提升正屏蔽效应。
(2) 同轴共面双裂纹钢丝试样的疲劳寿命要低于单裂纹钢丝试样,同轴共面双裂纹钢丝的负屏蔽效应随着裂纹间周向角度的减小和从裂纹尺寸的增大而增强。
(3) 利用ABAQUS和FRANC3D联合仿真计算所得到的单裂纹钢丝疲劳寿命仿真计算值与试验疲劳寿命值具有良好的拟合度,而双裂纹钢丝试样疲劳寿命仿真计算值与试验值的拟合度相对不理想。
(4) 同轴平行双裂纹钢丝试样的疲劳寿命可采用单裂纹假定利用仿真方法进行评估,同轴共面双裂纹钢丝试样的疲劳寿命须在单裂纹假定仿真分析结果的基础上考虑进行合理折减。
| [1] |
EL-ARISS B. Stiffness of reinforced concrete beams with external tendons[J].
Engineering Structures, 2004, 26(14): 2047-2051.
DOI:10.1016/j.engstruct.2004.04.009 |
| [2] |
王力力, 易伟建. 斜拉索的腐蚀案例与分析[J]. 公路工程, 2007, 32(1): 93-98. WANG Lili, YI Weijian. Cases analysis on cable corrosion of cable-stayed bridges[J]. Highway Engineering, 2007, 32(1): 93-98. DOI:10.3969/j.issn.1674-0610.2007.01.023 |
| [3] |
洪华, 曹素功, 傅俊磊, 等. 悬索桥主缆钢丝在持力状态下的表观腐蚀规律试验研究[J]. 公路交通科技, 2022, 39(6): 97-102. HONG Hua, CAO Sugong, FU Junlei, et al. Experimental study on apparent corrosion rule of main cable steel wires of suspension bridge in holding force state[J]. Journal of Highway and Transportation Research and Development, 2022, 39(6): 97-102. DOI:10.3969/j.issn.1002-0268.2022.06.013 |
| [4] |
BETTI R, WEST A C, VERMAAS G, et al. Corrosion and embrittlement in high-strength wires of suspension bridge cables[J].
Journal of Bridge Engineering, 2005, 10(2): 151-162.
DOI:10.1061/(ASCE)1084-0702(2005)10:2(151) |
| [5] |
BETTI R, YANEV B. Conditions of suspension bridge cables: New York city case study[J].
Transportation Research Record, 1999, 1654(1): 105-112.
DOI:10.3141/1654-12 |
| [6] |
LI H, LAN C M, JU Y, et al. Experimental and numerical study of the fatigue properties of corroded parallel wire cables[J].
Journal of Bridge Engineering, 2012, 17(2): 211-220.
DOI:10.1061/(ASCE)BE.1943-5592.0000235 |
| [7] |
MAYRBAURL R M, CAMO S. Guidelines for inspection and strength evaluation of suspension bridge parallel-wire cables[M].
Washington D.C.: Transportation Research Board, 2004.
|
| [8] |
LI S L, XU Y, ZHU S Y, et al. Probabilistic deterioration model of high-strength steel wires and its application to bridge cables[J].
Structure and Infrastructure Engineering, 2015, 11(9): 1240-1249.
DOI:10.1080/15732479.2014.948462 |
| [9] |
MEDVED J J, BRETON M, IRVING P E. Corrosion pit size distributions and fatigue lives: A study of the EIFS technique for fatigue design in the presence of corrosion[J].
International Journal of Fatigue, 2004, 26(1): 71-80.
DOI:10.1016/S0142-1123(03)00069-0 |
| [10] |
ZHAO T L, LIU Z Y, DU C W, et al. Modeling for corrosion fatigue crack initiation life based on corrosion kinetics and equivalent initial flaw size theory[J].
Corrosion Science, 2018, 142: 277-283.
DOI:10.1016/j.corsci.2018.07.031 |
| [11] |
郁大照, 陈跃良, 柳文林, 等. 服役环境下腐蚀坑等效为表面裂纹的有效性分析[J]. 应用力学学报, 2011, 28(1): 79-84, 112. YU Dazhao, CHEN Yueliang, LIU Wenlin, et al. Analysis of validation of real pit as surface crack under service environment[J]. Chinese Journal of Applied Mechanics, 2011, 28(1): 79-84, 112. |
| [12] |
CHEN J, DIAO B, HE J J, et al. Equivalent surface defect model for fatigue life prediction of steel reinforcing bars with pitting corrosion[J].
International Journal of Fatigue, 2018, 110: 153-161.
DOI:10.1016/j.ijfatigue.2018.01.019 |
| [13] |
LIU Z X, GUO T, YU X M, et al. Corrosion fatigue and electrochemical behaviour of steel wires used in bridge cables[J].
Fatigue & Fracture of Engineering Materials & Structures, 2021, 44(1): 63-73.
|
| [14] |
JIANG J H, MA A B, WENG W F, et al. Corrosion fatigue performance of pre-split steel wires for high strength bridge cables[J].
Fatigue & Fracture of Engineering Materials & Structures, 2009, 32(9): 769-779.
|
| [15] |
JIANG C, WU C, JIANG X. Experimental study on fatigue performance of corroded high-strength steel wires used in bridges[J].
Construction & Building Materials, 2018, 187(3): 681-690.
|
| [16] |
WANG G D, MA Y F, WANG L, et al. Experimental study and residual fatigue life assessment of corroded high-tensile steel wires using 3D scanning technology[J].
Engineering Failure Analysis, 2021, 124: 105335.
DOI:10.1016/j.engfailanal.2021.105335 |
| [17] |
郑祥隆, 谢旭, 李晓章, 等. 钢丝裂纹扩展估算模型及其在预腐蚀疲劳寿命计算中的应用[J]. 土木工程学报, 2017, 50(3): 101-107. ZHENG Xianglong, XIE Xu, LI Xiaozhang, et al. Estimation model for steel wire crack propagation and its application in calculation of pre-corrosion fatigue life[J]. China Civil Engineering Journal, 2017, 50(3): 101-107. |
| [18] |
MIAO C Q, LI R, YU J. Effects of characteristic parameters of corrosion pits on the fatigue life of the steel wires[J].
Journal of Constructional Steel Research, 2020, 168: 105879.
DOI:10.1016/j.jcsr.2019.105879 |
| [19] |
YE H W, DUAN Z C, TANG S Q, et al. Fatigue crack growth and interaction of bridge wire with multiple surface cracks[J].
Engineering Failure Analysis, 2020, 116: 104739.
DOI:10.1016/j.engfailanal.2020.104739 |
| [20] |
张洪, 李明阳, 王良辉, 等. 平行钢绞线拉索剩余承载力计算和疲劳寿命评估[J]. 公路交通科技, 2024, 41(12): 116-127. ZHANG Hong, LI Mingyang, WANG Lianghui, et al. Residual bearing capacity calculation and fatigue life evaluation on parallel steel strand cable[J]. Journal of Highway and Transportation Research and Development, 2024, 41(12): 116-127. DOI:10.3969/j.issn.1002-0268.2024.12.013 |
| [21] |
叶华文, 黄云, 王义强, 等. 基于临界域法的桥梁钢丝腐蚀疲劳寿命[J]. 西南交通大学学报, 2015, 50(2): 294-299. YE Huawen, HUANG Yun, WANG Yiqiang, et al. Fatigue life estimation of corroded bridge wires based on theory of critical distances[J]. Journal of Southwest Jiaotong University, 2015, 50(2): 294-299. DOI:10.3969/j.issn.0258-2724.2015.02.013 |
| [22] |
许红胜, 胡亚斯, 颜东煌. 既有腐蚀拉索钢丝蚀坑形态参数的分布特征[J]. 中外公路, 2020, 40(1): 80-84. XUE Hongsheng, HU Yasi, YAN Donghuang. Distribution character of morphology parameters of pits on existing corroded cable wires[J]. Journal of China and Foreign Highway, 2020, 40(1): 80-84. |
| [23] |
LAM K Y, PHUA S P. Multiple crack interaction and its effect on stress intensity factor[J].
Engineering Fracture Mechanics, 1991, 40(3): 585-592.
DOI:10.1016/0013-7944(91)90152-Q |
| [24] |
JIANG Z D, ZEGHLOUL A, BEZINE G, et al. Stress intensity factors of parallel cracks in a finite width sheet[J].
Engineering Fracture Mechanics, 1990, 35(6): 1073-1079.
DOI:10.1016/0013-7944(90)90135-4 |
| [25] |
HAN Z C, QIAN C F, LI H F. Study of the shielding interactions between double cracks on crack growth behaviors under fatigue loading[J].
Metals, 2020, 10(2): 202.
DOI:10.3390/met10020202 |
| [26] |
彭建新, 方兴, 周亚栋. 随机点蚀对Q550E钢试件抗拉力学性能的影响[J]. 公路交通科技, 2023, 40(8): 79-88. PENG Jianxing, FANG Xing, ZHOU Yadong. Influence of stochastic pitting corrosion on tensile mechanical performance of Q550E steel specimen[J]. Journal of Highway and Transportation Research and Development, 2023, 40(8): 79-88. DOI:10.3969/j.issn.1002-0268.2023.08.012 |
| [27] |
MAHMOUD K M. Fracture strength for a high strength steel bridge cable wire with a surface crack[J].
Theoretical and Applied Fracture Mechanics, 2007, 48(2): 152-160.
DOI:10.1016/j.tafmec.2007.05.006 |
| [28] |
MAYRBAURL R M, CAMO S. Cracking and fracture of suspension bridge wire[J].
Journal of Bridge Engineering, 2001, 6(6): 645-650.
DOI:10.1061/(ASCE)1084-0702(2001)6:6(645) |
| [29] |
张川. 含腐蚀损伤金属材料剩余寿命与剩余强度研究[D]. 南京: 南京航空航天大学, 2012. ZHANG Chuan. Research on residual life and residual strength of metals with corrosion damage[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. |
| [30] |
NAKAMURA S, SUZUMURA K. Experimental study on fatigue strength of corroded bridge wires[J].
Journal of Bridge Engineering, 2013, 18: 200-209.
DOI:10.1061/(ASCE)BE.1943-5592.0000366 |
| [31] |
吴冲, 蒋超, 姜旭. 预腐蚀桥梁缆索高强钢丝疲劳试验[J]. 同济大学学报(自然科学版), 2018, 46(12): 1622-1627. WU Chong, JIANG Chao, JIANG Xu. Experiment research on fatigue performance of pre-corroded high-strength bridge wires[J]. Journal of Tongji University (Natural Science), 2018, 46(12): 1622-1627. DOI:10.11908/j.issn.0253-374x.2018.12.002 |
 2025, Vol. 42
2025, Vol. 42



 ,
,