扩展功能
文章信息
- 侯越, 杨萍, 林伟, 崔菡珂.
- HOU Yue, YANG Ping, LIN Wei, CUI Hanke
- 时空信息融合下的车道级交通流预测
- Lane-level traffic flow prediction based on spatio-temporal fusion
- 公路交通科技, 2025, 42(6): 32-41
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(6): 32-41
- 10.3969/j.issn.1002-0268.2025.06.003
-
文章历史
- 收稿日期: 2023-10-13
2. 甘肃省公安厅交通警察总队, 甘肃 兰州 730000
2. Traffic Police Division of Gansu Provincial Public Security Department, Lanzhou, Gansu 730000, China
全国车辆保有量的快速增加,造成城市交通拥堵的问题日益严峻。城市道路运行状况受时间和空间的制约,而传统的交通流预测大都以路段为研究对象,对车道级空间相关性和交通数据的时间依赖特性考虑不足,致使建立的模型无法精准捕捉道路运行状况。因此,准确预测交通运行状态对于人们选择更合理的出行路线,降低交通拥堵风险具有十分重要的现实意义[1]。
交通流预测方法分为统计学习建模方法和机器学习建模方法。统计学习模型ARIMA[2]、卡尔曼滤波[3]等模型可依据时间序列估计交通流的变化,但在处理具有随机性的问题中存在局限性,不能捕捉非线性关系。以KNN[4], SVR[5]和RF[6]为代表的机器学习方法[7]因能较好拟合非线性数据,在交通领域得到广泛应用。随着深度学习的发展,以LSTM[8],GRU[9]为代表的循环神经网络为交通流时间特性建模提供有效思路,通过调节模型输入数据的时间窗口,可捕获交通流的长时依赖或短时依赖特征,但无法有效提取空间特征。杜圣东[10]使用注意力机制与LSTM组件,实现了数据时空特征的提取。Zheng[11]将路网空间关系组织为ODC矩阵,同时将该矩阵输入LSTM,实现时空特征的有效捕捉。冯凤江[12]通过GCN提取交通流空间特性的同时,结合BiGRU组件实现时间序列特征的有效挖掘。为进一步提升模型的特征提取能力,王九胜[13]提出了引入注意力机制与交互学习策略的时空关系特征提取模块,以达到捕捉数据时空特性关系的目的。上述文献主要从道路上下游空间关系角度出发进行建模,并未充分考虑多尺度长时依赖关系。Gu[14]叠加LSTM和GRU层建立预测模型,较为充分地考虑了车道空间关联性,并取得较好预测效果,但该过程未考虑多时间尺度依赖关系。
近年来,Transformer[15]凭借其突出的序列和非局部建模能力,在交通流预测[16-19]中得到广泛应用。Wu[20]提出Autoformer模型,实现了时间依赖性的充分提取。Tsai[21]基于Transformer提出一种多模态注意力改进策略,进一步扩展了其在跨模态领域的应用。
从交通流数据的时空特征来看,现有研究大多考虑路段间的关联性,忽略了相邻车道交通流数据的横向相关性;另外,交通流数据在时间维度上存在强依赖性,深入挖掘多时间尺度依赖关系才能获得更理想的预测结果。对此,本研究提出交通流组合预测模型Transformer-Encoder-stacked-GRU。首先借助Transformer-Encoder的位置编码将具有横向空间强相关的车道分别进行编码,得到输入数据的时间依赖特征。其次,依据注意力机制对车道级横向空间特性及参数相关性进行融合,以学习横向车道空间关系、多元参数相关性以及时间依赖特征。最后,采用stacked-GRU模型补充对交通流短时时间依赖特征的提取,同时,为避免重要参量特性的减弱,将特征融合矩阵和目标车道的流量序列矩阵拼接作为stacked-GRU模型的输入,实现考虑车道级横向空间特征与多时间尺度依赖特征的交通流数据预测。
1 交通流时空特性分析 1.1 交通流车道级时间特性断面交通流的时间特性表现为车辆运行过程中,其流量变化随时间演化呈现出一定规律性[22]。为反映同一车道相邻工作日交通流数据间的时间依赖关系,本研究使用合肥市天智-黄山路交叉口6号检测器的1号车道流量数据为研究对象,分析工作日2016.7.11—2016.7.15期间的时间关联特性,其结果以热力图的方式展现,具体如图 1所示。分析图 1可知,每个工作日间的车道流量关联程度均高于0.8,呈高度相关,可见车道未来交通流量的变化规律强依赖于历史交通流,即交通流的时间特性,进一步验证了在流量预测模型中考虑交通流时间特性的必要性。

|
| 图 1 6号检测器1号车道工作日流量热力图 Fig. 1 Workday traffic flow heat map with detector No.6 in lane No.1 |
| |
1.2 交通流车道级横向空间特性
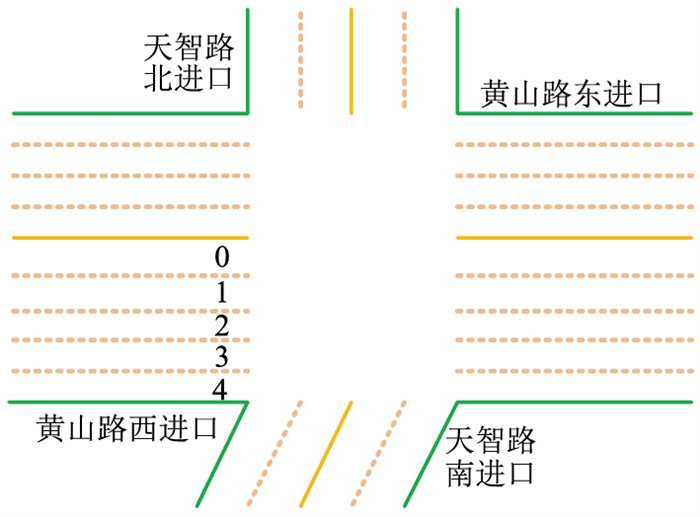
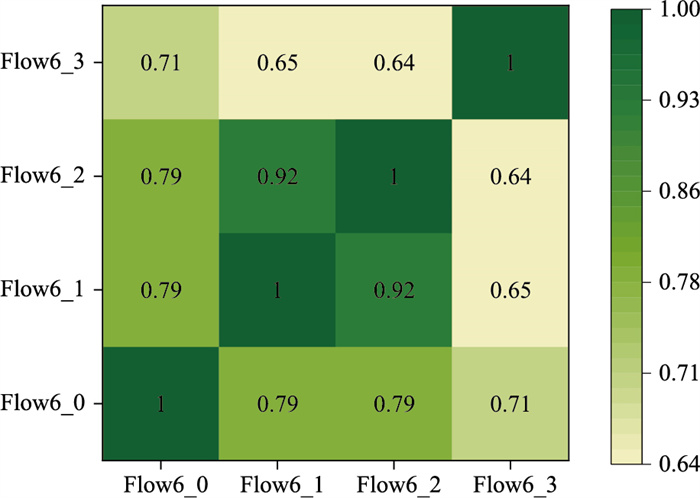
交通流的空间特性指道路网络结构上的交通流量分布情况,反映在现实路网中又分为不同路段间交通数据相互影响,以及相同路段不同车道间的关联程度上。本研究从分析同一路段不同车道间交通流序列关系出发,研究车道级横向空间特性。数据来源于合肥市天智-黄山路交叉口6号检测器,其拓扑示意图如图 2所示。由于其传感器存在数据丢失,缺少4号车道数据,本研究仅针对0~3号车道进行分析,各车道车流行驶方向均一致,相邻车道间交通流数据具有较高的关联程度。为挖掘不同车道交通流数据空间相关性,图 3为选自时间跨度为2016年7月11日至2016年7月25日间的6号检测器的黄山路西进口的0~3号车道流量热力图。通过观察不同车道交通流数据整体分布情况可知,1号目标车道和2号间车道流量关联程度为0.92,呈强相关关系,与其余车道呈中度相关关系。因此,对于研究的目标车道而言,考虑其横向空间相关的2号车道影响,能进一步提高预测模型的效果。
|
| 图 2 交叉口拓扑图 Fig. 2 Topological map of road intersection |
| |
|
| 图 3 6号检测器车道流量热力图 Fig. 3 Lane traffic flow heat map with detector No.6 |
| |
2 Transformer-Encoder融合架构 2.1 Transformer-Encoder车道级数据融合框架
本研究采用Transformer-Encoder实现车道级数据融合,相较于原Transformer-Encoder架构,将目标车道与该车道强相关的车道交通流数据共同作为输入,以此实现考虑时间依赖特性和车道级横向空间特性的数据融合。其具体过程如下:
(1) 时间窗口输入数据的位置编码(PE):为学习交通流序列数据的相对时序关系,捕捉时间相关性,分别在奇、偶位置处添加cos和sin变量,以减短编码长度。具体实现如式(1),式(2)所示。
| $ P E_{(p o s, 2 i)}=\sin \left(p o s / 10\;000^{2 i / d_{\text {model }}}\right), $ | (1) |
| $ P E_{(p o s, 2 i+1)}=\cos \left(p o s / 10\;000^{2 i / d_{\text {model }}}\right), $ | (2) |
式中,pos为时间窗口中车道特征位置;i为特征维度;dmodel为特征的最大维度。
通过微波6号检测器数据的车道级空间相关性分析,1号,2号车道具有横向空间强相关,对其分别进行编码,得到编码数组Xpos1,Xpos2。在此基础上,分别与原车道参数数据X1和X2进行嵌入得到考虑时序问题的新数据组织Xembedding1,Xembedding2。
| $ X_{\text {embedding } 1}=X_1+X_{\mathit {pos }^1}, $ | (3) |
| $ X_{\text {embedding }^2}=X_2+X_{\mathit {pos }^2}, $ | (4) |
(2) 基于多头注意力机制的横向车道级特征融合(MHA):为实现车道数据的时空特征融合和表示学习,使用可学习的权重矩阵WQ,WK和WV分别与数据组织Xembedding1,Xembedding2进行线性映射后得到同一维度的矩阵Q,K,V,其计算公式如下:
| $ \boldsymbol{Q}=X_{\text {embedding }^2} \cdot \boldsymbol{W}_Q, $ | (5) |
| $ \boldsymbol{K}=X_{\text {embedding }^1} \cdot \boldsymbol{W}_K, $ | (6) |
| $ \boldsymbol{V}=X_{\text {embedding }^1} \cdot \boldsymbol{W}_{V \circ} $ | (7) |
由于输入数据不同,K,V为1号车道映射的数据矩阵;Q为映射横向相关2号车道的数据矩阵,最后通过Attention计算输出时空特征融合后的结果:
| $ \begin{gathered} X_{\text {attention }}=\mathit{Attention}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})= \\ \mathit { softmax }\left(\frac{\boldsymbol{Q} \boldsymbol{K}^{\mathrm{T}}}{\sqrt{d_{\mathrm{k}}}}\right) \boldsymbol{V}, \end{gathered} $ | (8) |
式中,dk为矩阵K的维度;Attention(·, ·, ·)为注意力融合函数。
(3) 前向传播:通过计算得到误差损失。
(4) 残差连接与层标准化(A & N):为防止传输过程中梯度消失的问题,挖掘更深层次时空特征关联性、捕捉长期依赖和稳定模型训练,分别使用残差连接和层标准化对Xattention2=X2+Xpos2进行更新:
| $ X_{\mathit {attention }}=X+X_{\mathit {attention }}, $ | (9) |
| $ X_{\mathit {attention }}=\mathit { LayerNorm }\left(X_{\mathit {attention }}\right)_{\circ} $ | (10) |
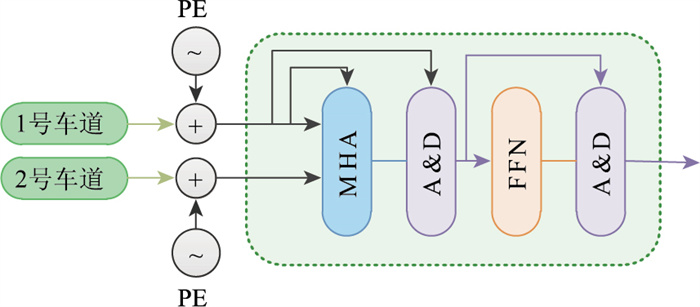
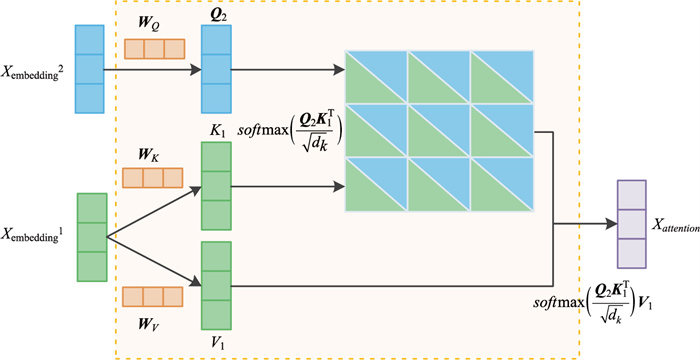
利用正余弦函数根据车道特征位置和维度变化生成位置编码,以学习时间相关性;通过多头注意力机制捕获横向相关车道数据,并进行时空特性融合;在此基础上,使用残差连接和层标准化进一步挖掘深层次时空特征,以此建立车道级融合框架,具体结构如图 4所示。图 5为横向车道级特征融合过程。
|
| 图 4 基于车道融合的Transformer-Encoder框架 Fig. 4 Lane-fusion based Transformer-Encoder framework |
| |
|
| 图 5 基于注意力机制的横向车道级特征融合计算 Fig. 5 Attention mechanism based lateral lane-level feature fusion calculation |
| |
2.2 Transformer-Encoder-stacked-GRU组合深度学习模型
为细粒化提取车道级空间特征与时间依赖特征,本研究提出Transformer-Encoder-stacked-GRU组合预测模型,图 6为模型总体架构图,以6号检测器的1号车道流量数据为研究对象,分析横向空间关系中具有强相关性的2号车道对1号车道的影响,按照时序数据序列,结合交通流流量和速度参数,构造多车道时序多元参数的输入矩阵。通过Transformer-Encoder中的位置编码提取输入矩阵的时间依赖特征,结合注意力机制完成车道级横向空间特征与参数相关性特征提取,以此构建特征融合矩阵。GRU模型因参数量少,更容易训练,常用于获取交通流数据的时间特性[23]。因此,本研究通过构建stacked-GRU模块来弥补短时依赖特征提取不充分的缺陷,同时,为避免特征融合过程中重要参数特性削减的问题,在特征融合矩阵基础上,通过加入目标车道流量数据作为后续模型输入,以达到强化重要特征的目的,并通过调节输入数据的时间窗口,完成多时间尺度依赖下的车道级流量预测。

|
| 图 6 Transformer-Encoder-stacked-GRU组合深度学习模型 Fig. 6 Deep learning model with Transformer-Encoder-stacked-GRU combination |
| |
3 试验验证 3.1 数据集描述
为验证模型的有效性,在合肥市示范区OpenITS数据集上进行试验验证。试验以合肥市天智-黄山路交叉口1, 2号车道为研究对象,并将6号检测器收集的交通数据作为试验数据集。数据集时间跨度为2016年7月11日至2016年7月25日。由于夜间车流量较少,导致整体数据的异常值增多,故去除22 : 00—5 : 00间的交通流量数据并以5 min划分一次时间段重构数据,一天共计192组数据。在此基础上,本研究通过对缺失值的相邻上下时间片参数均值化的方式对缺失值进行填充。试验将7月11日—7月21日共3 164条数据作为训练集,将7月22日—7月25日共1 150条数据作为测试集。表 1为对1号,2号车道交通数据预处理后的数据集。所有试验在Python3.7平台上开发,编译器为Pycharm,使用配备Intel(R) Core(TM) i7-11800H @2.70 GHz处理器和16 G内存的计算机。
| 时间 | 1号车道流量数据/veh | 1号车道平均速度/(km·h―1) | 2号车道流量数据/veh | 2号车道平均速度/(km·h―1) |
| … | … | … | … | … |
| 2016-7-11T12:00 | 41 | 43 | 36 | 48.5 |
| 2016-7-11T12:05 | 25 | 38.75 | 23 | 47.25 |
| 2016-7-11T12:10 | 9 | 34.5 | 10 | 46 |
| 2016-7-11T12:15 | 37 | 45.1 | 32 | 47.71 |
| 2016-7-11T12:20 | 40 | 46.3 | 29 | 43.67 |
| 2016-7-11T12:25 | 26 | 44.43 | 23 | 47.64 |
| 2016-7-11T12:30 | 31 | 42.5 | 26 | 43.11 |
| … | … | … | … | … |
3.2 结果分析
为验证横向空间特性和多时间尺度依赖对预测模型的影响,本研究以不同时间窗口的组合预测模型为基准,为实现不同模型流量预测效果对比,同时引入MAPE,MAE,MSE和RMSE作为误差评价指标,分别记为eMAP,eMA, eMS, eRMS, 各评价指标公式如下:
| $ e_{\mathrm{MAP}}=\frac{100 \%}{n} \sum\limits_{i=1}^n\left|\frac{y_i^{\text {predict }}-y_i^{\text {true }}}{y_i^{\text {true }}}\right|, $ | (11) |
| $ e_{\mathrm{MA}}=\frac{1}{n} \sum\limits_{i=1}^n\left|y_i^{\text {predict }}-y_i^{\text {true }}\right|, $ | (12) |
| $ e_{\mathrm{MS}}=\frac{1}{n} \sum\limits_{i=1}^n\left(y_i^{\text {predict }}-y_i^{\text {true }}\right)^2, $ | (13) |
| $ e_{\mathrm{RMS}}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(y_i^{\text {predict }}-y_i^{\text {true }}\right)^2}, $ | (14) |
式中,yipredict为预测值;yitrue为真实值;n为样本个数。
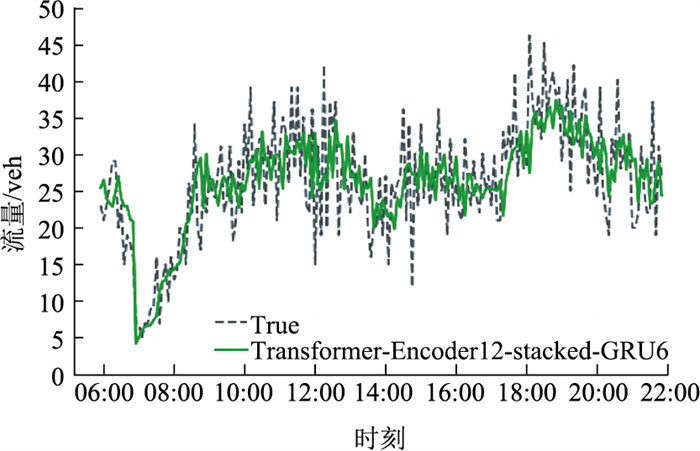
3.2.1 预测时间窗口为6的试验结果选取12个时间窗口的1,2车道时序多元参数输入矩阵经Transformer-Encoder车道融合框架得到特征融合矩阵,并拼接目标车道流量序列矩阵生成GRU模型的输入参数,选取6个时间窗口数据作为输入预测未来30 min的交通流量。图 7为本节所提方法(Transformer-Encoder12-stacked-GRU6)的7月23日流量预测图,图中纵坐标为流量数据,横坐标表示7月23日剔除夜晚22 : 00至清晨5 : 00后的当天时间,从图中可以看出,车流量具有早、午和晚高峰的特征。从拟合曲线来看,本节所提方法预测的误差度较低,预测曲线的变化趋势与真实曲线的变化规律基本符合,能够较好地拟合真实曲线,表明本节模型是一种有效的交通流预测方法。
|
| 图 7 Transformer-Encoder12-stacked-GRU6流量预测 Fig. 7 Flow prediction with Transformer-Encoder12-stacked-GRU6 |
| |
为显化各模型预测效果,将7月23日各模型预测的早、午、晚高峰结果可视化为图 8所示,横、纵坐标分别表示时间和交通流量。其中,True为真实流量数据,Transformer-Encoder12-stacked-GRU6为本研究所提模型,stacked-GRU6、stacked-LSTM6分别为单时间窗口模型预测曲线,Transformer-Encoder6-stacked-GRU6表示仅考虑横向空间关系的预测模型。由图 8可知,stacked-GRU6与stacked-LSTM6曲线较为相似,在流量相对平稳的时间段内表现出较好的预测效果,但在极值点附近起伏波动较大,而Transformer-Encoder6-stacked-GRU6和Transformer-Encoder12-stacked-GRU6模型由于考虑了车道级横向空间关系,其拟合曲线更贴近真实值,相较于基准线模型其预测结果均有显著提升。

|
| 图 8 7月23日各时间段模型流量预测 Fig. 8 Modeled flow predictions by period on July 23rd |
| |
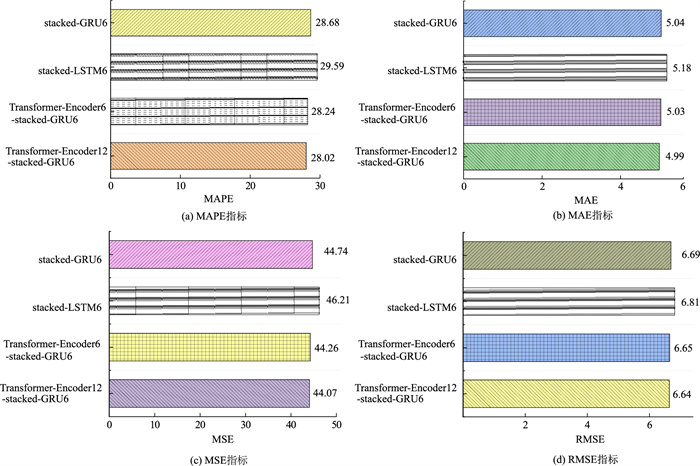
表 2为本节模型所用均值填充方法与中位数、邻近数据填充方法的客观评价指标对比,从表 2可以看出,使用均值法进行数据填充的MAPE虽略高于对比算法,但MAE,MSE,RMSE性能指标均为最低,由此说明填充方法对数据分布情况具有较强的针对性,而本研究选用方法具有普遍适用性,填充结果更贴合实际交通数据,能更好地提升模型预测性能。图 9为本节模型与对比模型的客观评价指标对比。从图 9可以看出,本节所提考虑车道级横向空间特性和多时间尺度依赖的Transformer-Encoder12-stacked-GRU6模型的MAPE,MAE,MSE,RMSE值分别为28.02,4.99,44.07,6.64,相比于基本模型和仅考虑横向空间特性的模型,本节所提模型的4个指标均最小,其中MAPE降低最多,降低了0.78%~5.31%,说明本节所提模型能较好地捕捉到数据的变化趋势和波动性,具有较好的预测精度。stacked-GRU6模型的MSE值相较于stacked-LSTM6模型降低了3.18%,说明stacked-GRU6模型的预测值与真实值间具有较低的误差。而融入Transformer-Encoder架构后的Transformer-Encoder6-stacked-GRU6模型,细粒化考虑了车道级横向空间特性与参数相关性,其预测效果优于仅考虑单一时间依赖的模型。在此基础上,进一步考虑多时间尺度依赖的Transformer-Encoder12-stacked-GRU6模型,其预测误差相对改善,模型预测精度也高于未考虑多时间尺度依赖的Transformer-Encoder6-stacked-GRU6模型。
| 数据填充方法 | MAPE | MAE | MSE | RMSE |
| 均值 | 28.02 | 4.99 | 44.07 | 6.64 |
| 中位数 | 27.84 | 5.06 | 45.17 | 6.72 |
| 邻近数据 | 27.84 | 5.08 | 45.44 | 6.74 |
|
| 图 9 时间窗口为6的各模型预测性能指标 Fig. 9 Prediction performance indicators of various models with time window of 6 |
| |
3.2.2 预测时间窗口为12的试验结果
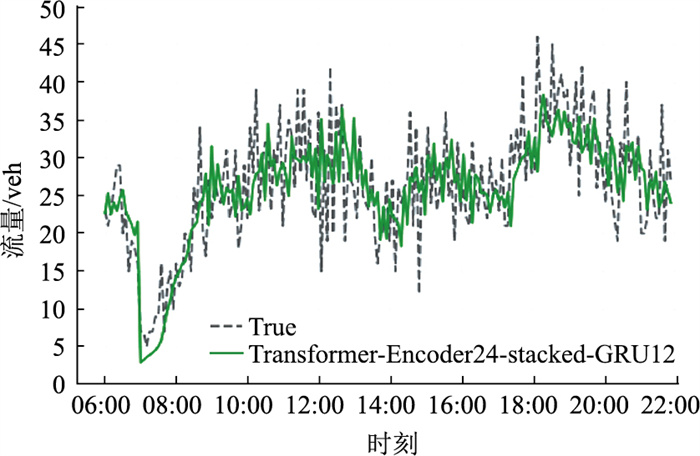
选取24个时间窗口的1,2车道时序多元参数输入矩阵经Transformer-Encoder车道融合框架得到特征融合矩阵,并拼接目标车道流量序列矩阵生成GRU模型的输入参数,选取12个时间窗口数据作为输入预测未来1 h的交通流量。图 10为本节模型(Transformer-Encoder24-stacked-GRU12)在7月23日剔除夜晚22 : 00—清晨5 : 00数据后的真实值与预测值的对比效果图,从图中可以看出,所提模型的预测曲线与真实曲线在早、午和晚高峰的变化趋势基本符合,具有较好的拟合效果,表明本节所提方法是一种有效的交通流预测方法。
|
| 图 10 Transformer-Encoder24-stacked-GRU12流量预测 Fig. 10 Flow prediction with Transformer-Encoder24-stacked-GRU12 |
| |
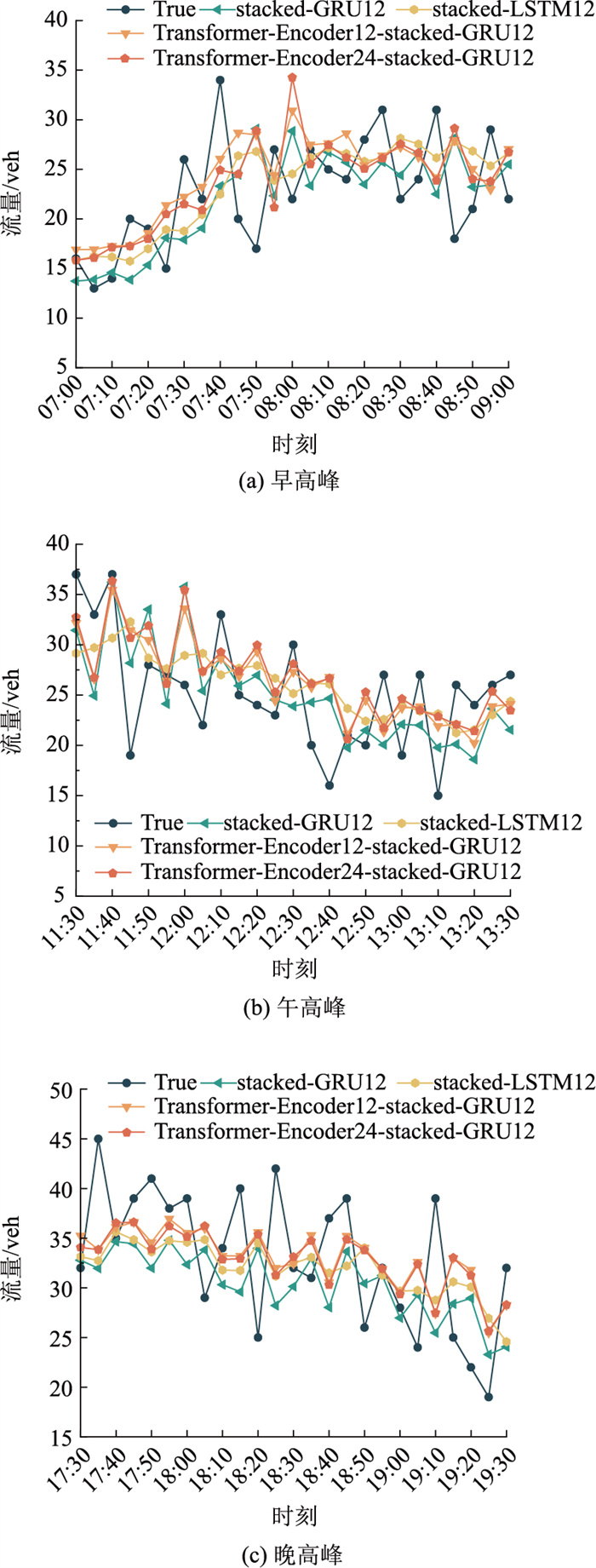
图 11分别为各模型在7月23日的早、午和晚高峰对比图。其中,True为真实数据曲线,stacked-GRU12、stacked-LSTM12为仅考虑时间依赖的单车道模型预测曲线,Transformer-Encoder12-stacked-GRU12表示仅考虑横向空间关系的模型预测曲线,Transformer-Encoder24-stacked-GRU12表示考虑多时间尺度和车道横向空间关系的模型预测曲线。从对比图中可看出,Transformer-Encoder24-stacked-GRU12模型在流量变化幅度较大时与真实数据具有相近变化趋势,说明该模型预测效果较好,较为接近真实数据。而stacked-LSTM12模型预测性能在真实流量数据大于40的位置预测效果较好。
|
| 图 11 各时间段模型的流量预测 Fig. 11 Modeled flow predictions by period |
| |
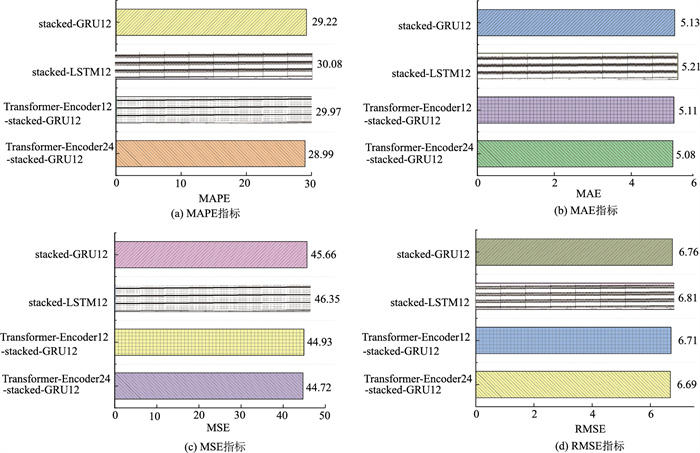
图 12为时间窗口为12的各模型预测性能指标,通过评价指标MAPE,MAE,MSE和RMSE来量化模型的性能,指标数值越小,说明真实值与预测值之间的误差越低,预测精度越高。从指标数据可以看出,在单一时间依赖的模型中,stacked-GRU-12模型的误差值均低于stacked-LSTM12模型,说明相比于stacked-LSTM12,该模型预测结果具有更小波动性和更高的预测精度。而Transformer-Encoder12-stacked-GRU12的MAE,MSE和RMSE相较于stacked-GRU12分别降低0.39%,1.60%和0.74%,说明考虑车道级空间关联特性与参数相关性能更准确捕捉到交通流量变化趋势,具有较好的预测效果。调节Transformer-Encoder输入数据的时间窗口建立多时间尺度依赖特性与车道级横向空间特性的Transformer-Encoder24-stacked-GRU12预测模型,其预测精度高于考虑车道级横向空间特征的Transformer-Encoder12-stacked-GRU12,以此说明了考虑多时间尺度依赖特性的必要性。
|
| 图 12 时间窗口为12的各模型预测性能指标 Fig. 12 Prediction performance indicators of various models with time window of 12 |
| |
综合图 9和图 12数据可知:本研究所提模型相较于仅考虑横向空间关系及单时间预测窗口模型,其预测性能具有较大提升。进一步表明,考虑不同时间尺度和车道横向空间相关性能够细粒化挖掘时空关系,提高预测精度,为交管部门评估交通运行状态提供切实参考意义。
4 结论本研究旨在解决现有方法未能充分考虑交通流横向空间特征、时间序列关系的问题,从细粒化挖掘时空关联性、多元参数相关性的角度出发,将Transformer-Encoder引入至交通流预测中构建Transformer-Encoder-stacked-GRU组合深度学习模型。通过位置编码表征不同时间窗口下输入数据相对位置的方式,捕捉交通流序列间长时依赖关系。同时,为动态学习到交通流数据的横向变化关系,运用注意力机制将捕捉到的关联特征进行融合,得到特征融合矩阵,用特征融合矩阵替换Transformer-Encoder的自注意力矩阵,以挖掘车道级空间关系与时间依赖的时空特征;使用stacked-GRU模型补充对交通流短时时间依赖特征的提取,通过调节输入数据的时间窗口大小,将特征融合矩阵和目标车道的流量序列矩阵拼接输入到stacked-GRU模型中,建立基于车道级交通流预测的模型架构。通过对比试验分析可知,无论是在预测时间窗口为6还是12的模型中,该模型的MAPE,MAE,MSE,RMSE都最低,其中MAPE降低最多,相较于Transformer-Encoder6-stacked-GRU6、Transformer-Encoder12-stacked-GRU12模型在MAPE指标下分别降低0.78%,3.27%,同时相较于stacked-LSTM6和stacked-LSTM12模型在MAPE指标下分别降低5.31%,3.62%,进一步验证了考虑多时间尺度依赖和车道级横向空间特征在实际场景中进行交通流预测的重要性。未来研究将进一步优化Transformer-Encoder模型,完善车道级时空关系的一致提取。
| [1] |
张韫, 张波, 王剑楠, 等. 基于动态时空特征周期性编码的公路交通流量预测模型[J]. 公路交通科技, 2025, 42(3): 21-33. ZHANG Yun, ZHANG Bo, WANG Jiannan, et al. Highway traffic flow prediction model based on periodic encoding with dynamic spatio-temporal features[J]. Journal of Highway and Transportation Research and Development, 2025, 42(3): 21-33. DOI:10.3969/j.issn.1002-0268.2025.03.003 |
| [2] |
HOU Q, LENG J, MA G, et al. An adaptive hybrid model for short-term urban traffic flow prediction[J/OL]. Physica A: Statistical Mechanics and its Applications, 2019, 527: 121065. https://doi.org/10.1016/j.physa. 2019.121065.
|
| [3] |
EMAMI A, SARVI M, ASADI BAGLOEE S. Using Kalman filter algorithm for short-term traffic flow prediction in a connected vehicle environment[J].
Journal of Modern Transportation, 2019, 27(3): 222-232.
DOI:10.1007/s40534-019-0193-2 |
| [4] |
赵亚伟, 陈艳晶, 管伟. 基于多维时间序列的ETC短时交通流量预测模型[J]. 交通运输系统工程与信息, 2016, 16(4): 191-198. ZHAO Yawei, CHEN Yanjing, GUAN Wei. Prediction model of ETC short term traffic flow based on multidimensional time series[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(4): 191-198. |
| [5] |
傅贵, 韩国强, 逯峰, 等. 基于支持向量机回归的短时交通流预测模型[J]. 华南理工大学学报(自然科学版), 2013, 41(9): 71-76. FU Gui, HAN Guoqiang, LU Feng, et al. Short-term traffic flow forecasting model based on support vector machine regression[J]. Journal of South China University of Technology(Natural Science Edition), 2013, 41(9): 71-76. |
| [6] |
ZHANG L Z, ALHARBE N R, LUO G C, et al. A hybrid forecasting framework based on support vector regression with a modified genetic algorithm and a random forest for traffic flow prediction[J].
Tsinghua Science and Technology, 2018, 23(4): 479-492.
DOI:10.26599/TST.2018.9010045 |
| [7] |
黄振盛, 汪玉美, 韩江洪, 等. 基于MLS-SVM和时空特性的短时交通流量预测方法[J]. 合肥工业大学学报(自然科学版), 2020, 43(1): 57-63. HUANG Zhensheng, WANG Yumei, HAN Jianghong, et al. Short-term urban traffic flow prediction based on MLS-SVM and spatiotemporal features[J]. Journal of Hefei University of Technology (Natural Science Edition), 2020, 43(1): 57-63. |
| [8] |
MA X L, TAO Z M, WANG Y H, et al. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data[J].
Transportation Research Part C: Emerging Technologies, 2015, 54: 187-197.
DOI:10.1016/j.trc.2015.03.014 |
| [9] |
凤少伟, 凤超, 申浩. 基于K-means与GRU的短时交通流预测研究[J]. 计算机技术与发展, 2020, 30(7): 125-129. FENG Shaowei, FENG Chao, SHEN Hao. Research on short-term traffic flow prediction based on K-means and GRU[J]. Computer Technology and Development, 2020, 30(7): 125-129. |
| [10] |
杜圣东, 李天瑞, 杨燕, 等. 一种基于序列到序列时空注意力学习的交通流预测模型[J]. 计算机研究与发展, 2020, 57(8): 1715-1728. DU Shengdong, LI Tianrui, YANG Yan, et al. A sequence-o-sequence spatial-temporal attention learning model for urban traffic flow prediction[J]. Journal of Computer Research and Development, 2020, 57(8): 1715-1728. |
| [11] |
ZHENG Z, CHEN W, WU X, et al. LSTM network: A deep learning approach for short-term traffic forecast[J].
Iet Intelligent Transport Systems, 2017, 11(2): 68-75.
|
| [12] |
冯凤江, 杨增刊. 基于图卷积和注意力机制的高速公路交通流预测[J]. 公路交通科技, 2023, 40(9): 215-223. FENG Fengjiang, YANG Zengkan. Expressway traffic flow forecast based on graph convolution and attention mechanism[J]. Journal of Highway and Transportation Research and Development, 2023, 40(9): 215-223. DOI:10.3969/j.issn.1002-0268.2023.09.025 |
| [13] |
王九胜, 许辉, 缪中岩. 基于时空关系的多细粒度隧道交通流预测模型研究与应用[J]. 公路交通科技, 2024, 41(11): 86-93. WANG Jiusheng, XU Hui, MIAO Zhongyan. Study and application of multi fine-grained tunnel traffic flow prediction model based on spatio-temporal relation[J]. Journal of Highway and Transportation Research and Development, 2024, 41(11): 86-93. DOI:10.3969/j.issn.1002-0268.2024.11.010 |
| [14] |
GU Y L, LU W Q, QIN L Q, et al. Short-term prediction of lane-level traffic speeds: A fusion deep learning model[J].
Transportation Research Part C: Emerging Technologies, 2019, 106: 1-16.
|
| [15] |
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[J].
Advances in Neural Information Processing Systems, 2017, 30: 20750-20762.
|
| [16] |
GUO S N, LIN Y F, FENG N, et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting[C]//Proceedings of the AAAI conference on artificial intelligence. Hawaii: AAAI, 2019, 33(1): 922-929.
|
| [17] |
CAI L, JANOWICZ K, MAI G, et al. Traffic transformer: Capturing the continuity and periodicity of time series for traffic forecasting[J].
Transactions in GIS, 2020, 24(3): 736-755.
|
| [18] |
WEN Y, XU P, LI Z, et al. RPConvformer: A novel Transformer-based deep neural networks for traffic flow prediction[J/OL]. Expert Systems with Applications, 2023, 218: 119587. https://doi.org/10.1016/j.eswa.2023.119587
|
| [19] |
WANG F, XIN X J, LEI Z W, et al. Transformer-based spatio-temporal traffic prediction for access and metro networks[J].
Journal of Lightwave Technology, 2024, 42(15): 5204-5213.
|
| [20] |
WU H X, XU J H, WANG J M, et al. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting[J].
Advances in Neural Information Processing Systems, 2021, 34: 22419-22430.
|
| [21] |
TSAI Y H H, BAI S, LIANG P P, et al. Multimodal transformer for unaligned multimodal language sequences[C]//Proceedings of the Conference. Association for Computational Linguistics. Meeting. Florence: Association for Computational Linguistics, 2019, 2019: 6558-6569.
|
| [22] |
张文松, 姚荣涵. 基于时空特性和组合深度学习的交通流参数估计[J]. 交通运输系统工程与信息, 2021, 21(1): 82-89. ZHANG Wensong, YAO Ronghan. Traffic flow parameters estimation based on spatio-temporal characteristics and hybrid deep learning[J]. Journal of Transportation Systems Engineering and Information Technology, 2021, 21(1): 82-89. |
| [23] |
SHU W N, CAI K, XIONG N N. A short-term traffic flow prediction model based on an improved gate recurrent unit neural network[J].
IEEE Transactions on Intelligent Transportation Systems, 2021, 23(9): 16654-16665.
|
 2025, Vol. 42
2025, Vol. 42



 ,
,