扩展功能
文章信息
- 唐进君, 段一鑫, 商淑杰, 王骋程, 陈群.
- TANG Jinjun, DUAN Yixin, SHANG Shujie, WANG Chengcheng, CHEN Qun
- 多特征融合时空图卷积的高速公路交通流量预测
- Expressway traffic volume prediction based on feature-fused spatio-temporal graph convolutional networks
- 公路交通科技, 2025, 42(6): 22-31
- Journal of Highway and Transportation Research and Denelopment, 2025, 42(6): 22-31
- 10.3969/j.issn.1002-0268.2025.06.002
-
文章历史
- 收稿日期: 2023-05-29
2. 山东高速基础设施建设有限公司, 山东 济南 250000;
3. 山东省交通规划设计院集团有限公司, 山东 济南 250000
2. Shandong Hi-speed Infrastructure Construction Co., Ltd., Jinan, Shandong 250000, China;
3. Shandong Provincial Communications Planning and Design Institute Group Co., Ltd., Jinan, Shandong 250000, China
随着中国经济的高速发展,跨省贸易、跨省旅游等出行行为日益增加,高速公路成为人们长距离出行的主要选择。与此同时,高速公路拥堵问题日益加剧,并且由于高速公路上的车辆行驶速度较快,一旦出现拥堵,事故的发生几率和严重程度将大幅增加。为了缓解高速公路交通拥堵,高速公路主动管控措施成为交通管理部门和专家学者关注的热点,而科学的主动管控离不开对交通状态的准确把控。精准的交通流预测可以为主动管控的功能实施提供支持,例如可变限速[1]、主动匝道控制[2]、路径诱导[3]等。现有的交通流预测方法主要分为3类:基于统计学的预测方法、基于机器学习的预测方法和基于深度学习的预测方法。
在交通流预测发展早期,大部分方法都是考虑交通流的时间关联性,用统计的方法分析其未来趋势得到预测结果。其中,历史平均(Historic Average,HA)模型是将过去一段时间内的平均流量作为未来预测结果。虽然HA模型简单易行,但由于交通流具有非线性、动态性等特点,其预测效果较差。卡尔曼滤波(Kalman Filtering)[4]模型是通过递推算法对交通状态进行线性估计,从而预测出未来交通量。该模型利用了大量历史数据学习时间变化特征,但是对非平稳序列预测效果不佳。差分移动自回归(Autoregressive Integrated Moving Average,ARIMA)模型[5]是将数据差分后得到平稳序列再进行时序预测,解决了卡尔曼滤波模型在非平稳序列上的局限性。
随着机器学习方法的快速发展,许多学者将机器学习应用于交通流预测中,并取得了不错的效果。Hong[6]将支持向量回归(Support Vector Regression,SVR)和禁忌搜索算法结合起来预测高速公路交通量。Sun[7]提出一种基于贝叶斯网络的交通流预测方法,该方法将相邻道路之间的交通流建模成贝叶斯网络,在不完整数据上也有较好效果。虽然机器学习方法相比于统计学方法能够更好地发现交通流的非线性特征,预测精度也更高,但是难以深度挖掘交通流内部的隐藏时空关系。
由于深度学习在模型结构和训练效果等方面具有明显的优势,所以在面对许多高维度、大规模的数据挖掘问题中表现出了很好的有效性和鲁棒性[8]。Ma[9]使用长短时记忆(Long Short-Term Memory,LSTM)神经网络模型来提取交通流的时间动态特征,预测交通流速度。Fu[10]使用门控循环单元(Gated Recurrent Unit,GRU)模型预测交通流量,GRU比LSTM少了一个门,能在参数更少的情况下达到类似的效果。但是,LSTM和GRU都只捕获了交通流的时间关联性而忽略了交通流还具有空间关联性。为了捕获交通流的时空关联性,Yu[11]提出了一种新的时空图卷积网络(Spatio-Temporal Graph Convolutional Networks,STGCN)模型来预测交通量,该模型用图卷积网络(Graph Convolutional Networks,GCN)来捕获空间关系,用一维卷积捕获时间关系。Li[12]提出一种扩散卷积递归神经网络(Diffusion Convolutional Recurrent Neural Networks,DCRNN)模型,该模型使用图上的双向随机游走来捕获空间关联性,以及使用具有计划采样的编码器-解码器架构来捕获时间依赖性。Guo[13]提出一种基于注意力机制的时空图卷积网络(Attention Based Spatial-Temporal Graph Convolutional Networks,ASTGCN),该模型提出使用时空注意力机制来捕获交通流的动态时空相关性。Wu[14]认为明确的图结构不一定能反映出真正的依赖关系,因此提出了图波网络(Graph WaveNet)模型,该模型通过一种新的自适应依赖矩阵,可以精确地捕获数据中隐藏的空间关系。Song[15]提出一种时空同步图卷积网络(Spatial-Temporal Synchronous Graph Convolutional Networks,STSGCN)模型,该模型设计了一种局部时空图结构,可以同时提取交通流时空关联性。冯凤江[16]基于注意力机制的Seq2Seq模型提出了一种考虑时空分布的高速公路短时交通流多步预测方法。王九胜[17]基于自注意力机制学习时空依赖性来预测交通流。陈建忠[18]对生成对抗网络的生成器和判别器进行重构,改进了损失函数,来提升包含缺失值的交通流预测精度。
在现实世界中,路网上的交通量不仅与自身的时空特征密切相关,还会受到很多外部因素的影响。比如,在自由流条件下,速度越快、车道越多,相应的交通量也会越高;雨雪天气下更容易出现交通拥堵[19]。现有的研究虽然融合了交通流的时空关联性,但是没有综合考虑影响交通流变化的外部因素,例如:车道数、限速值、天气等。
为了充分考虑外部特征和时空关系对交通流量的影响,进而提高高速公路流量预测精度,本研究提出一种多维特征融合的时空图卷积网络模型(Feature-fused Spatio-Temporal Graph Convolutional Networks,FSTGCN)来预测高速公路交通流量。主要贡献点如下。
(1) 考虑了限速和天气等外部特征对交通流量的影响。提出了特征卷积网络(Feature Convolutional Networks,FCN)来捕捉外部特征与交通流之间的关联性。
(2) 考虑了交通流内部的时空关联性。将交通路网视为图,使用GCN来捕捉节点间的空间关联性,并加入残差连接减少过拟合。使用GRU捕捉交通流的时间关联性。
(3) 在山东省的真实路网上进行了模型评价。试验表明,FSTGCN模型在长短期预测中均优于对比模型,并且能保持较好的稳定性。
1 FSTGCN模型 1.1 交通流量预测问题定义高速公路上布设的龙门架可以实时检测通过该门架的车型、车辆数等动态数据。依照现行的《公路工程技术标准》对每条数据按照车辆类型进行交通量换算,得到在单位时间内通过该门架的标准车辆数,每种车型对应的交通量系数见表 1。路网中所有龙门架可构成一张拓扑图G= (V, E), 其中门架节点集合V= {V1, V2, …, VN},N为节点数量;E为图中边的集合。邻接矩阵 A ∈ R N×N表征节点间的空间关系,其中若Vij∈E,则Aij=1,否则等于0。流量矩阵 X t∈ R为在t时刻N个节点的流量,图 1为用图结构表示的交通数据。外部特征F t∈ R N×P为在t时刻N个节点的P个特征。
| 系数 | 车型 |
| 1.0 | 客一、客二、货一、专一 |
| 1.5 | 客三、客四、货二、专二 |
| 2.5 | 货三、专三 |
| 4.0 | 货四、货五、货六、专四、专五、专六 |

|
| 图 1 图结构的交通数据 Fig. 1 Traffic data with graph structure |
| |
交通流量预测的目标是找到一个函数f,这个函数可以根据图G、流量矩阵 X t和外部特征 F t算出未来T′时段的流量矩阵,函数映射关系如式(1)所示。
| $ \left(\boldsymbol{X}^{t+T^{\prime}}, \cdots, \boldsymbol{X}^{t+1}\right)=f\left(\left(\boldsymbol{X}^t, \cdots, \boldsymbol{X}^{t-T+1}\right) ; \boldsymbol{F}^t ; G\right) 。$ | (1) |
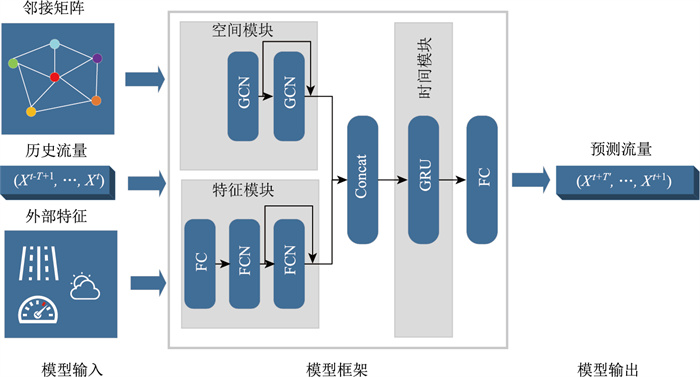
为了提取交通流的空间关联性,设计了空间模块,其中包含2个GCN层,并且在2个GCN层之间使用残差连接来减少过拟合。为了捕捉外部特征与交通流之间的关联性,设计了特征模块,其中包含1个全连接(Fully Connected, FC)层和2个FCN层,同样在2个FCN层之间采用了残差连接来减少过拟合。为了捕捉交通流的时间关联性,设计了时间模块,其中包含1个GRU层。FSTGCN模型框架如图 2所示,由空间模块、特征模块、时间模块和全连接层组成,将空间模块的输出和时间模块的输出连接后输入到时间模块,最后使用一个全连接层作为输出层。
|
| 图 2 FSTGCN模型框架 Fig. 2 FSTGCN model structure |
| |
1.3 空间关系建模
交通网络是一种典型的非欧几里德结构的数据,因此可以用图来更好地表征交通网络。由于传统的CNN在拓扑图中无法保持平移不变性,无法对拓扑图进行空间特征提取。GCN基于图谱理论在傅里叶域对图信号进行卷积操作,使得其能够处理非欧几里得结构的图数据, 故使用GCN学习交通网络的空间特征。
处理图结构首先要获得输入信号x的拉普拉斯矩阵L = D - Α,对L进行对称归一化可得L ′∈ R I×I:
| $ \begin{gathered} \boldsymbol{L}^{\prime}=\boldsymbol{D}^{-\frac{1}{2}} \boldsymbol{L} \boldsymbol{D}^{-\frac{1}{2}}=\boldsymbol{D}^{-\frac{1}{2}}(\boldsymbol{D}-\boldsymbol{A}) \boldsymbol{D}^{-\frac{1}{2}}= \\ \boldsymbol{I}_N-\boldsymbol{D}^{-\frac{1}{2}} \boldsymbol{A} \boldsymbol{D}^{-\frac{1}{2}}, \end{gathered} $ | (2) |
式中,L ′为对称归一化拉普拉斯矩阵;I N为单位矩阵;A 为图G的邻接矩阵;D 为 A 的度矩阵,
| $ \boldsymbol{L}^{\prime}=\boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{U}^{-1}=\boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{U}^{\mathrm{T}}, $ | (3) |
式中,U = (u1, …, ui)为分解后的特征向量;Λ =diag ([λ1, …, λi])是由特征值组成的对角矩阵。因为U为正交矩阵,所以U ―1= U T。
基于图谱理论,图上的频谱卷积可视为信号x与傅里叶域内的卷积核的乘积:
| $ (\boldsymbol{x} * \boldsymbol{g})_G=\boldsymbol{U}\left(\left(\boldsymbol{U}^{\mathrm{T}} \boldsymbol{g}\right)\left(\boldsymbol{U}^{\mathrm{T}} \boldsymbol{x}\right)\right) \Rightarrow \boldsymbol{x} * \boldsymbol{g}_\theta=\boldsymbol{U}_{g_q} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{x}, $ | (4) |
式中,g θ= U T g 为卷积核;*为卷积操作;θ为模型参数。由于式(4)计算复杂度高,所以Defferrard[20]将卷积核定义为对角矩阵的切比雪夫多项式,式(4)可转化为:
| $ \boldsymbol{x} * \boldsymbol{g}_\theta=\sum\limits_{k=0}^K \theta_k T_k(\overline{\boldsymbol{L}}) \boldsymbol{x}, $ | (5) |
式中,
| $ \begin{gathered} \boldsymbol{x} * \boldsymbol{g}_\theta=\theta_0 \boldsymbol{x}+\theta_1(\overline{\boldsymbol{L}}) x=\theta_0 \boldsymbol{x}+\theta_1\left(\boldsymbol{U} \overline{\boldsymbol{\Lambda}} \boldsymbol{U}^{\mathrm{T}}\right) \boldsymbol{x}= \\ \theta_0 \boldsymbol{x}+\theta_1\left(\boldsymbol{U}\left(\boldsymbol{\Lambda}-\boldsymbol{I}_N\right) \boldsymbol{U}^{\mathrm{T}}\right) \boldsymbol{x}=\theta_0 \boldsymbol{x}+ \\ \theta_1\left(\boldsymbol{U} \boldsymbol{\Lambda} \boldsymbol{U}^{\mathrm{T}}-\boldsymbol{I}_N\right) \boldsymbol{x}=\theta_0 \boldsymbol{x}-\theta_1\left(\boldsymbol{D}^{-\frac{1}{2}} \boldsymbol{A} \boldsymbol{D}^{-\frac{1}{2}}\right) \boldsymbol{x} 。\end{gathered} $ | (6) |
为了预防过拟合和梯度爆炸,定义θ=θ0=-θ1,
| $ \boldsymbol{x} * \boldsymbol{g}_\theta=\theta\left(\boldsymbol{I}_N+\boldsymbol{D}^{-\frac{1}{2}} \boldsymbol{A} \boldsymbol{D}^{-\frac{1}{2}}\right) x=\theta\left(\tilde{\boldsymbol{D}}^{-\frac{1}{2}} \tilde{\boldsymbol{A}} \tilde{\boldsymbol{D}}^{-\frac{1}{2}}\right) \boldsymbol{x}_{\circ} $ | (7) |
总结以上公式推导可得,第l层GCN的输出为:
| $ \begin{gathered} \boldsymbol{H}(l)=f(\boldsymbol{H}(l-1), \boldsymbol{A})= \\ \sigma\left(\tilde{\boldsymbol{D}}^{-\frac{1}{2}} \tilde{\boldsymbol{A}} \tilde{\boldsymbol{D}}^{-\frac{1}{2}} \boldsymbol{H}(l-1) \boldsymbol{W}(l-1)\right), \end{gathered} $ | (8) |
式中,σ为激活函数;W (l-1)为第l-1层的权重。因此,给定图信号 x 和邻接矩阵 A ,GCN可以通过对输入节点的频谱进行卷积来提取空间特征。
空间模块采用了两层GCN来提取交通流的空间特征,并且在第1层GCN和第2层GCN之间加入了残差连接。因此,结合式(8)可得出空间模块的计算公式:
| $ \left\{\begin{array}{l} \boldsymbol{y}_1=\operatorname{ReLU}\left(\tilde{\boldsymbol{D}}^{-\frac{1}{2}} \tilde{\boldsymbol{A}} \tilde{\boldsymbol{D}}^{-\frac{1}{2}} \boldsymbol{x} \boldsymbol{W}_0\right) \\ \boldsymbol{y}_2=\operatorname{ReLU}\left(\tilde{\boldsymbol{D}}^{-\frac{1}{2}} \tilde{\boldsymbol{A}} \tilde{\boldsymbol{D}}^{-\frac{1}{2}} \boldsymbol{y}_1 \boldsymbol{W}_1\right)+\boldsymbol{y}_1 \end{array}, \right. $ | (9) |
式中,y1为第1层GCN的输出;y2为空间模块的输出;ReLU为非线性激活函数。
1.4 特征关系建模除了历史交通流信息,其他的一些因素也会影响到交通流大小,比如:道路宽度、限速值和天气状况。道路宽度和限速值都属于数值型变量,天气状况属于类别变量,所以需要对天气状况进行编码。本研究采用索引编码,即假设天气状况有5种类别,则对应的5种类别分别编码为[1, 2, 3, 4, 5]。外部特征的特征矩阵记为 F t,其表达式为:
| $ \boldsymbol{F}^t=\left(\begin{array}{ccc} f_{11} & \cdots & f_{1 P} \\ \vdots & \ddots & \vdots \\ f_{N 1} & \cdots & f_{N P} \end{array}\right) $ | (10) |
为了有效地学习外部特征对交通流量的影响,本研究提出了一个特征卷积网络(FCN)。FCN是一种提取静态的节点特征与动态的时序特征之间相关性的方法。特征模块以特征矩阵和流量矩阵作为输入,将节点特征与历史流量进行特征融合。定义特征卷积核 X′ ∈ R N×T为交通量 X 与特征矩阵 F t的乘积,其中 X = (X t, …, X t-T+1),其表达式如式(11)所示:
| $ x_{i t}^{\prime}=x_{i t} \sum\limits_{j=1}^P f_{i j}, $ | (11) |
式中,x′ it为 X ′中的元素,i∈ (1, N), t∈ (1, T);xit为 X 中的元素。特征卷积计算过程可用图 3表示。
|
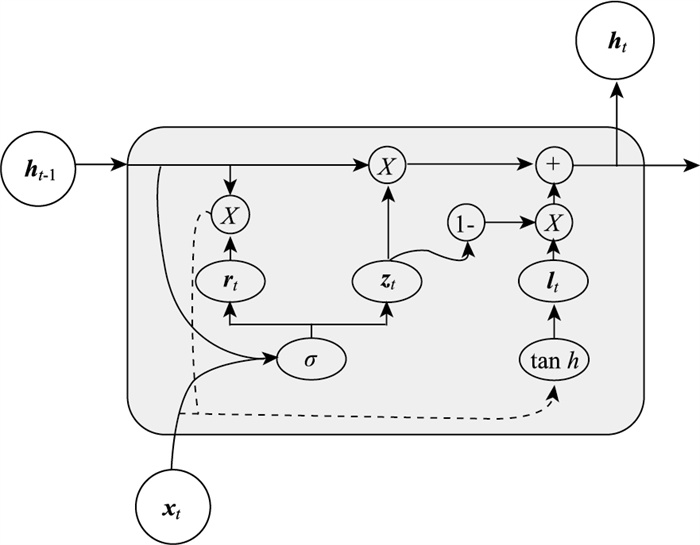
| 图 3 GRU结构 Fig. 3 GRU structure |
| |
因此,FCN的计算公式如式(12)所示:
| $ f=\sigma\left(\boldsymbol{X}^{\prime} \boldsymbol{W}+\boldsymbol{b}\right), $ | (12) |
式中,σ为激活函数;W为权重;b为偏置。
为了使模型具有更强的泛化能力,在将原始特征矩阵输入到FCN层前使用一个全连接层用来扩展特征矩阵的维度。最终,特征模块包含一个全连接层,两个FCN层,且在第1个FCN层和第2个FCN层之间使用了残差连接。结合式(12)可得出特征模块的计算公式:
| $ \left\{\begin{array}{l} \boldsymbol{y}_1=\operatorname{ReLU}\left(\boldsymbol{X}^{\prime} \boldsymbol{W}_0+\boldsymbol{b}_0\right) \\ \boldsymbol{y}_2=\operatorname{ReLU}\left(\boldsymbol{y}_1^{\prime} \boldsymbol{W}_1+\boldsymbol{b}_1\right)+\boldsymbol{y}_1 \end{array}, \right. $ | (13) |
式中,y1为第1层FCN的输出;y2为空间模块的输出;X ′为交通量 X 和特征矩阵 F 的特征卷积;y ′ 1为第1层FCN的输出 y1和特征矩阵 F 的特征卷积。
1.5 时间关系建模交通流是一组时间序列,获取时间关联性是交通流量预测中的一个重要问题。目前,RNN是处理时间序列问题中最常用的神经网络模型。但是,因为RNN存在着梯度消失和梯度爆炸等问题,所以RNN不适合处理长时间序列。幸运的是,RNN的变体模型LSTM[21]和GRU[22]通过门控机制很好地解决了该问题。但是,由于LSTM模型结构复杂、训练时间长,而GRU比LSTM参数量更少,也更容易训练。因此,选择使用GRU模型来提取时间关系。
GRU结构如图 3所示,ht-1为t-1时刻的细胞单元留下的隐藏态,包含了前t-1个时刻的信息;x t为t时刻的交通流信息;r t为重置门,决定了旧的信息有多少能保留到当前时刻;z t为更新门,决定了如何将新的信息与旧的信息相结合;l t为t时刻所存储的信息;h t为时刻t输出的状态信息,其中包含了前t个时刻的信息。GRU内的计算方法如式(14)所示。
| $ \left\{\begin{array}{l} \boldsymbol{r}_t=\sigma\left(\boldsymbol{W}_r \boldsymbol{x}_t+\boldsymbol{U}_r \boldsymbol{h}_{t-1}\right) \\ \boldsymbol{z}_t=\sigma\left(\boldsymbol{W}_z \boldsymbol{x}_t+\boldsymbol{U}_z \boldsymbol{h}_{t-1}\right) \\ \boldsymbol{l}_t=\tanh \left(\boldsymbol{W} \boldsymbol{x}_t+\boldsymbol{U} \boldsymbol{r}_t \odot \boldsymbol{h}_{t-1}\right) \\ \boldsymbol{h}_t=\boldsymbol{z}_t \boldsymbol{h}_{t-1}+\left(1-\boldsymbol{z}_t\right) \boldsymbol{l}_t \end{array}, \right. $ | (14) |
式中,⊙为Hadamard乘积,即对应元素相乘;W和U是矩阵变换的权重。
2 数据采集与结果分析上一节对FSTGCN模型做了详细介绍,本节通过采集山东高速公路交通流量数据,对FSTGCN模型的预测效果进行验证,并与6种常用的交通流模型和3种消融模型进行对比试验,验证模型的有效性、鲁棒性和实时性。
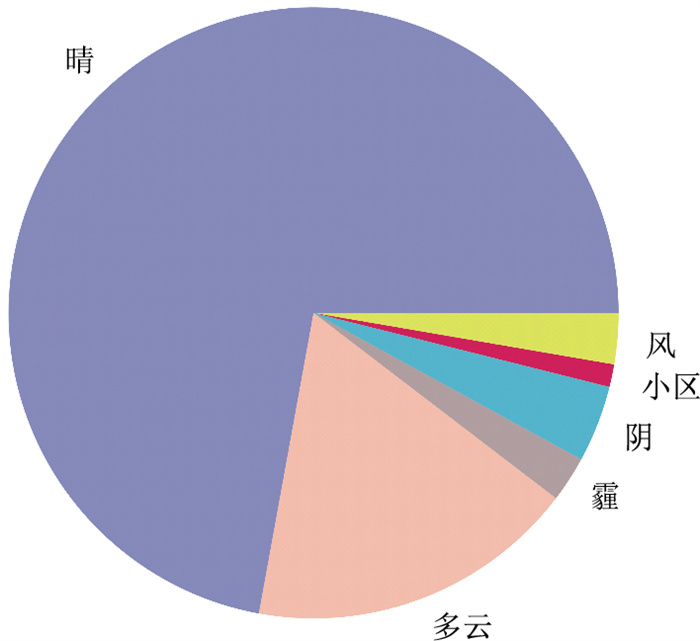
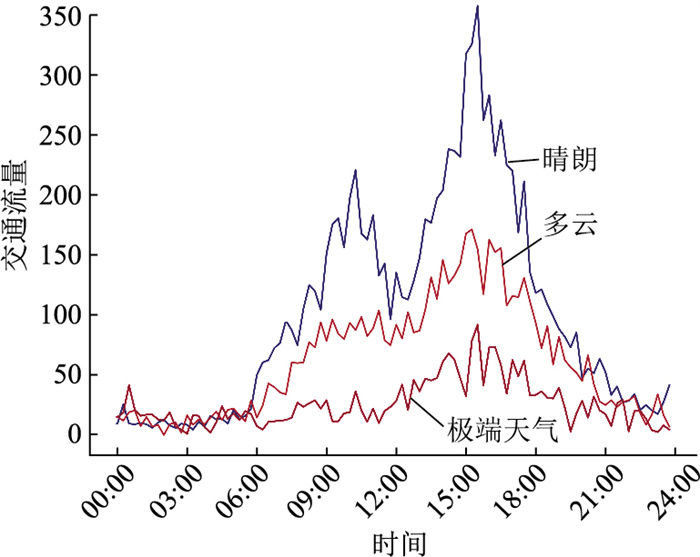
2.1 数据描述流量数据来源于山东省高速公路上门架检测装置,门架记录了每15 min内通过断面的车型及数量,因此可得到每个门架所处断面以15 min为间隔的交通流量。本研究所使用的数据包含了山东省41条高速公路上的1 029个门架,时间范围是从2020年1月1日至2020年1月10日。图数据是根据门架的经纬度匹配上最近的高速公路路段,再基于真实的位置关系确定图的邻接矩阵。特征数据包含3个字段:车道数、限速值和天气。车道数和限速值是每个节点所处路段对应的车道数和限速值的真实值; 天气根据节点所属城市当天的天气情况进行索引编码得出,本试验数据中出现了晴、多云、霾、阴、小雪和风6种天气类型,每种天气类型占比如图 4所示。因为霾、阴、小雪和风这4类天气在全部数据中占比较少,将它们各自作为一种天气属性容易造成过拟合。因此,本研究将这4种天气合并为一种天气属性,即极端天气。为了直观地展示天气对交通流量的影响,本研究选取一个具有3种天气类型的节点,绘制不同天气类型下的交通流量对比图。从图 5中可以看出,在6:00—18 : 00这个区间,晴天的交通流量依次大于多云天气和极端天气。3种特征的详细属性及编码方式见表 2。
|
| 图 4 不同天气类型饼状图 Fig. 4 Pie chart of different weather types |
| |
|
| 图 5 不同天气类型交通流量对比 Fig. 5 Traffic volume comparison with different weather types |
| |
| 类别 | 属性 | 编码方式 |
| 车道数 | 2,3,4 | 2,3,4 |
| 限速值/(km·h―1) | 80,100,120 | 80,100,120 |
| 天气 | 晴、多云、极端天气 | 1,2,3 |
由于不同节点间的数值差距较大,为了便于模型计算,本研究对每个节点的流量数据和每个类别的特征数据都进行了标准归一化处理。标准归一化是根据原始数据的均值和标准差进行数据的标准化处理。处理后的原始数据变为符合标准正态分布的数据,即平均值为0,标准差为1。
2.2 试验设置为了评估FSTGCN模型的效果,本研究采用了3种常用的指标来衡量模型性能:
(1) 平均绝对误差(Mean Absolute Error,MAE), 记为eMA:
| $ e_{\mathrm{MA}}=\frac{1}{n} \sum\limits_{i=1}^n\left|\hat{\boldsymbol{y}}_i-\boldsymbol{y}_i\right| \text { 。} $ | (15) |
(2) 均方根误差(Root Mean Squared Error,RMSE)记为eRMS:
| $ e_{\mathrm{RMS}}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(\hat{\boldsymbol{y}}_i-\boldsymbol{y}_i\right)^2} \text { 。} $ | (16) |
(3) 对称平均绝对百分比误差(Symmetric Mean Absolute Percentage Error,SMAPE), 记为eSMAP:
| $ e_{\mathrm{SMAP}}=\frac{1}{n} \sum\limits_{i=1}^n \frac{\left|\hat{\boldsymbol{y}}_i-\boldsymbol{y}_i\right|}{\left(\left|\hat{\boldsymbol{y}}_i\right|+\left|\boldsymbol{y}_i\right|\right) / 2} \times 100 \%, $ | (17) |
式中,
试验采用滑动窗口的方法生成数据集,历史窗口大小为12,未来窗口大小为4,即使用过去3 h的流量作为输入预测未来15,30,45,60 min的流量。80%的数据集作为训练集,20%的数据集作为验证集,使用Adam优化器训练模型,学习率为0.000 1。
深度学习模型的好坏在很大程度上取决于超参数的设置。FSTGCN模型中的超参数主要有两个。一是特征维度I,即特征模块中全连接层的维度,二是隐藏层维度H,即空间模块中GCN的维度和特征模块中FCN的维度。试验选择使用MAE作为评价指标来比较不同的I和H对试验结果的影响,从而确定I和H的最佳值。试验设定I的取值范围为[16, 32, 48, 64, 128],H的取值范围为[32, 48, 64, 96, 128]。通过网格搜索,得出当I=48且H=48时MAE最低。因此,本研究选定特征维度为48,隐藏层维度为48。
2.4 试验结果及分析为了评估FSTGCN模型的性能,与交通流预测中常用的6种模型作对比。同时,为了体现特征模块、空间模块和时间模块的作用,本研究还进行了FSTGCN模型的消融试验。
(1) 历史平均模型(HA)为使用过去1 h的平均流量作为未来的预测值。
(2) 差分移动自回归模型(ARIMA)为一种基于统计学的时间序列预测常用方法。
(3) 长短时记忆模型(LSTM)为一种RNN的变体模型。
(4) 门控循环单元模型(GRU)为详见1.5节时间关系建模部分。
(5) 时空图卷积模型(STGCN)[12]为融合时空关系的深度学习模型。
(6) 时间图卷积模型(T-GCN)[23]为融合GCN和GRU的交通流预测模型。
(7) FSTGCN-NF为去除了特征模块的FSTGCN模型。
(8) FSTGCN-NT为去除了时间模块的FSTGCN模型。
(9) FSTGCN-NGCN为去除了空间模块的FSTGCN模型。
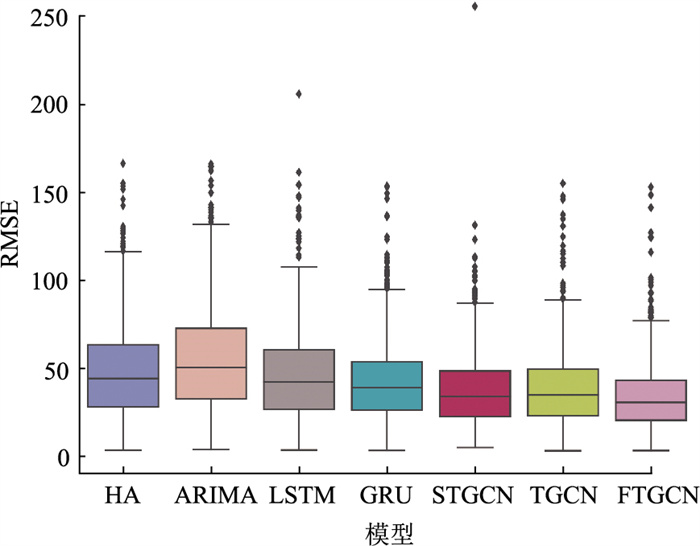
表 3比较了FSTGCN模型与6个基准模型和3个消融模型分别在15,30,45,60 min的预测性能。试验结果表明,本研究提出的FSTGCN模型在所有模型中表现出了最好的性能,它的性能优于HA、ARIMA,LSTM,GRU等传统模型。同时,它在不同时间步长的预测性能也超越了STGCN和T-GCN等基于图卷积的深度学习模型。相比于表 3中性能第二的基准模型STGCN,它在15 min和30 min的RMSE误差分别降低了3.68%和5.82%,在45 min和60 min的RMSE误差分别降低了9.97%和10. 81%。此外,相比于FSTGCN-NF,FSTGCN-NT和FSTGCN-NGCN这3种消融模型,FSTGCN模型也取得了最好的预测效果,说明了特征模块、时间模块和空间模块都对交通流量预测有正面作用。交通流的长期预测一直是一个巨大的挑战,试验测试了不同模型在短期预测(15,30 min)和长期预测(45,60 min)时的预测精度。如图 6所示,FSTGCN在短期和长期预测都优于所有基准模型。此外,从图 6中可以看出FSTGCN模型的RMSE变化曲线较为平缓,在4个时间步中,预测误差波动较小,说明本研究所提出的FSTGCN模型在长期预测和短期预测中都有较好的稳定性。图 7为不同模型的RMSE箱形图。
| 模型 | 15 min | 30 min | 45 min | 60 min | |||||||||||
| RMSE | MAE | SMAPE/% | RMSE | MAE | SMAPE/% | RMSE | MAE | SMAPE/% | RMSE | MAE | SMAPE/% | ||||
| HA | 37.67 | 25.96 | 19.46 | 43.54 | 29.87 | 21.97 | 49.65 | 34.14 | 24.75 | 55.82 | 38.53 | 27.59 | |||
| ARIMA | 43.18 | 30.24 | 22.77 | 48.45 | 33.93 | 25.25 | 54.06 | 38.01 | 27.98 | 59.14 | 41.68 | 30.51 | |||
| LSTM | 47.90 | 32.43 | 24.79 | 51.58 | 34.78 | 27.36 | 51.63 | 35.74 | 26.99 | 53.42 | 37.14 | 28.37 | |||
| GRU | 50.35 | 33.71 | 26.83 | 48.26 | 32.61 | 24.91 | 49.15 | 33.49 | 25.59 | 49.19 | 33.57 | 25.84 | |||
| STGCN | 38.54 | 25.99 | 19.60 | 39.54 | 25.99 | 21.35 | 42.51 | 28.53 | 21.19 | 43.39 | 29.31 | 21.81 | |||
| T-GCN | 42.88 | 29.17 | 22.29 | 44.44 | 30.55 | 23.35 | 43.56 | 29.79 | 22.71 | 43.98 | 29.94 | 23.19 | |||
| FSTGCN-NF | 38.07 | 26.07 | 20.91 | 39.68 | 27.13 | 21.98 | 40.67 | 27.92 | 22.36 | 41.50 | 28.55 | 22.64 | |||
| FSTGCN-NT | 37.27 | 26.24 | 21.27 | 40.56 | 28.24 | 22.32 | 43.18 | 29.94 | 23.30 | 46.00 | 31.92 | 24.40 | |||
| FSTGCN-NGCN | 39.78 | 26.77 | 21.13 | 40.58 | 27.33 | 21.41 | 40.79 | 27.48 | 21.39 | 41.06 | 27.64 | 21.66 | |||
| FSTGCN(ours) | 37.12 | 24.91 | 19.85 | 37.24 | 24.98 | 19.75 | 38.27 | 25.78 | 20.57 | 38.70 | 26.03 | 20.63 | |||

|
| 图 6 不同模型不同步长下的RMSE对比 Fig. 6 Comparison of RMSE with different models and different horizons |
| |
|
| 图 7 不同模型的RMSE箱形图 Fig. 7 RMSE box plot with different models |
| |
与基准模型中表现最好的模型STGCN对比,图 8分别展示了预测步长为15,30,45,60 min的连续24 h交通量预测效果对比。从图 8中可以看出本研究提出的FSTGCN相比于STGCN的预测效果更好,尤其是在45,60 min时,FSTGCN的预测值更加贴近于真实值。

|
| 图 8 24 h内的交通量预测对比 Fig. 8 Comparison of traffic volume prediction for 24 hours |
| |
高速公路交通流量预测更常用的场景是在大流量情况下,大流量时更容易出现交通拥堵。为了进一步评价FSTGCN模型在整个路网上的性能,尤其是在离群点的预测性能,本研究计算了FSTGCN模型与基准模型每个节点的RMSE,并用箱型图的方式可视化展示。如图 7所示,箱子中间的线是数据的中位数,代表了误差的平均大小,箱子内包含50%的数据,即箱子的宽度反映了误差的波动程度,上下两条线代表数据在统计学上的理论最大最小值,超出上限的黑点为数据中离群的点。这些离群点的数量越少,数值越小说明模型对极端值的预测性能越好,鲁棒性越高。表 4统计的是这些离群点的最大值和平均值。相比于LSTM模型,FSTGCN模型的最大RMSE减少了25.64%,平均RMSE减少了27.05%。相比于GRU模型,FSTGCN模型的最大RMSE减少了0.35%,平均RMSE减少了10.54%。相比于STGCN模型,FSTGCN模型的最大RMSE减少了40.13%,平均RMSE减少了6.99%。相比于TGCN模型,FSTGCN模型的最大RMSE减少了1.32%,平均RMSE减少了13.69%。因此,本研究提出的FSTGCN模型还具有较高的鲁棒性。
| 模型 | 最大值 | 平均值 |
| HA | 166.17 | 130.82 |
| ARIMA | 165.77 | 147.12 |
| LSTM | 205.52 | 137.45 |
| GRU | 153.36 | 112.08 |
| STGCN | 255.26 | 107.81 |
| TGCN | 154.87 | 116.18 |
| FSTGCN | 152.83 | 100.27 |
实时性也是交通流量预测任务中的一个重要指标。实际中,交通流量预测任务都要求在短时间内给出精度较高的预测结果,进而辅助交通管理者做出其他决策。因此,本试验计算了LSTM,GRU,STGCN,TGCN和FSTGCN模型的训练时长和预测时长,不考虑HA和ARIMA模型是因为它们的预测精度较差。因为它们的预测时长均小于1 s,所以本研究主要对比它们的训练时长。如表 5所示,FSTGCN模型相比于LSTM和GRU模型因为增加了空间模块和特征模块,训练时间更长,但仍在可接受范围内。FSTGCN模型相比于STGCN和TGCN模型,不仅在精度上有所提升,训练时长也更短。因此,本研究提出的FSTGCN模型在实时性方面也具有优越性。
3 结论
(1) 本研究提出了一种融合多维特征的FSTGCN交通流量预测模型。在FSTGCN中使用特征模块来捕获交通外部特征和交通流量之间的相关性,使用空间模块来捕获交通流量的空间相关性,使用时间模块来提取交通流量的时间关联性。
(2) 通过采集山东省高速公路交通流量数据,并进行模型验证,与HA,ARIMA,LSTM,GRU,STGCN和T-GCN等传统模型进行对比试验。结果表明,本研究提出的FSTGCN模型在长短期预测中具有优势,且在短期预测和长期预测中都能保持较好的稳定性。此外,试验还证明了FSTGCN模型具有较好的鲁棒性和实时性。
(3) 消融试验结果表明,特征模块、空间模块和时间模块都能提高交通流量预测精度。其中特征模块对模型的性能提升尤为明显,并且能够从交通流数据和外部特征数据中充分挖掘出二者之间的相关性。
| [1] |
曹国平. 基于多源数据融合的高速公路可变限速动态管控方法研究[D]. 西安: 长安大学, 2021. CAO Guoping. Research on dynamic control method of variable speed limit on expressway based on multi-source data fusion[D]. Xi'an: Chang'an University, 2021. |
| [2] |
王健. 基于ETC系统数据的高速公路主动管控建设探讨[J]. 中国交通信息化, 2020(12): 99-101. WANG Jian. Discussion on the construction of active control of highway based on ETC system data[J]. China ITS Journal, 2020(12): 99-101. |
| [3] |
房崇鑫. 基于深度学习的短时交通流预测及其路径诱导的研究与实现[D]. 扬州: 扬州大学, 2021. FANG Chongxin. Research and implementation of short-term traffic flow prediction and its path induction based on deep learning[D]. Yangzhou: Yangzhou University, 2021. |
| [4] |
KUMAR S V. Traffic flow prediction using kalman filtering technique[J].
Procedia Engineering, 2017, 187: 582-587.
DOI:10.1016/j.proeng.2017.04.417 |
| [5] |
SMITH B, WILLIAMS B, OSWALD R. Comparison of parametric and nonparametric models for traffic flow forecasting[J].
Transportation Research Part C: Emerging Technologies, 2002, 10(4): 303-321.
DOI:10.1016/S0968-090X(02)00009-8 |
| [6] |
HONG W C, PAI P F, YANG S L, et al. Highway traffic forecasting by support vector regression model with tabu search algorithms[C]//The 2006 IEEE International Joint Conference on Neural Network Proceedings. New York: IEEE, 2006: 1617-1621.
|
| [7] |
SUN S L, ZHANG C S, YU G Q. A bayesian network approach to traffic flow forecasting[J].
IEEE Transactions on Intelligent Transportation Systems, 2006, 7(1): 124-132.
DOI:10.1109/TITS.2006.869623 |
| [8] |
WANG Y, ZHANG D X, LIU Y, et al. Enhancing transportation systems via deep learning: A survey[J].
Transportation Research Part C: Emerging Technologies, 2019, 99: 144-163.
DOI:10.1016/j.trc.2018.12.004 |
| [9] |
MA X L, TAO Z M, WANG Y H, et al. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data[J].
Transportation Research Part C: Emerging Technologies, 2015, 54: 187-197.
DOI:10.1016/j.trc.2015.03.014 |
| [10] |
FU R, ZHANG Z, LI L. Using LSTM and GRU neural network methods for traffic flow prediction[C]//2016 31st Youth academic annual conference of Chinese Association of Automation (YAC). New York: IEEE, 2016: 324-328.
|
| [11] |
YU B, YIN H, ZHU Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting[C]//IJCAI'18: Proceedings of the 27th International Joint Conference on Artificial Intelligence. Washington, D.C. : AAAI, 2018: 3634-3640.
|
| [12] |
LI Y G, YU R, SHAHABI C, et al. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting[C]//International Conference on Learning Representations. Vancouver: OpenReview, 2018.
|
| [13] |
GUO S N, LIN Y F, FENG N, et al. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Washington, D.C. : AAAI, 2019: 922-929.
|
| [14] |
WU Z H, PAN S R, LONG G D, et al. Graph wave net for deep spatial-temporal graph modeling[C]//IJCAI '19: Proceedings of the 28th International Joint Conference on Artificial Intelligence. Macao: Morgan Kaufmann, 2019: 1907-1913.
|
| [15] |
SONG C, LIN Y F, GUO S N, et al. Spatial-temporal synchronous graph convolutional networks: A new framework for spatial-temporal network data forecasting[C]//Proceedings of the AAAI conference on artificial intelligence. Washington, D.C. : AAAI, 2020: 914-921.
|
| [16] |
冯凤江, 杨增刊. 基于图卷积和注意力机制的高速公路交通流预测[J]. 公路交通科技, 2023, 40(9): 215-223. FENG Fengjiang, YANG Zengkan. Expressway traffic flow forecast based on graph convolution and attention mechanism[J]. Journal of Highway and Transportation Research and Development, 2023, 40(9): 215-223. DOI:10.3969/j.issn.1002-0268.2023.09.025 |
| [17] |
王九胜, 戴许海, 缪中岩, 等. 基于多元时空关系的公路交通流量时序预测模型[J]. 公路交通科技, 2023, 40(10): 175-182. WANG Jiusheng, DAI Xuhai, LIAO Zhongyan, et al. A model for time series prediction on highway traffic flow based on multivariate spatio-temporal relationship[J]. Journal of Highway and Transportation Research and Development, 2023, 40(10): 175-182. DOI:10.3969/j.issn.1002-0268.2023.10.020 |
| [18] |
陈建忠, 吕泽凯, 蔺皓萌. 基于生成对抗和图卷积网络的含缺失值交通流预测模型[J]. 公路交通科技, 2023, 40(9): 205-214. CHEN Jianzhong, LV Zekai, LIN Haomeng. A prediction model for traffic flow with missing values based on generative adversarial and graph convolutional networks[J]. Journal of Highway and Transportation Research and Development, 2023, 40(9): 205-214. DOI:10.3969/j.issn.1002-0268.2023.09.024 |
| [19] |
徐月欣. 不同天气条件下的城市快速路交通拥堵评价与短时预测[D]. 西安: 长安大学, 2017. XU Yuexin. Evaluation and short-term prediction of traffic congestion on urban expressways under different weather conditions[D]. Xi'an: Chang'an University, 2017. |
| [20] |
DEFFERRARD M, BRESSON X, VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering[C]//NIPS'16: Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona: MIT Press, 2016: 3844-3852.
|
| [21] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J].
Neural Computation, 1997, 9(8): 1735-1780.
DOI:10.1162/neco.1997.9.8.1735 |
| [22] |
CHO K, VAN MERRIENBOER B, GULCEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation[C]//Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP). Doha: ACL, 2014: 1724-1734.
|
| [23] |
ZHAO L, SONG Y J, ZHANG C, et al. T-GCN: A temporal graph convolutional network for traffic prediction[J].
IEEE Transactions on Intelligent Transportation Systems, 2019, 21(9): 3848-3858.
|
 2025, Vol. 42
2025, Vol. 42



 ,
,