扩展功能
文章信息
- 张添翼, 杨涵, 田俊山, 王歆远.
- ZHANG Tian-yi, YANG Han, TIAN Jun-shan, WANG Xin-yuan
- K-means算法在高速公路ETC数据分析中的应用
- Application of K-means Algorithm in Expressway ETC Data Analysis
- 公路交通科技, 2024, 41(6): 199-206
- Journal of Highway and Transportation Research and Denelopment, 2024, 41(6): 199-206
- 10.3969/j.issn.1002-0268.2024.06.022
-
文章历史
- 收稿日期: 2024-04-24
2. 福建省高速公路科技创新研究院有限公司, 福建 福州 350001
2. Fujian Expressway Science and Technology Innovation Research Institute Co., Ltd., Fuzhou, Fujian 350001, China
2019年5月,交通运输部办公厅印发《关于大力推动高速公路ETC发展应用工作的通知》以来,我国ETC用户累计数量剧增[1]。在高速公路路网运行过程中,产生了大量的ETC数据集。ETC数据集中,出入口数据、牌识数据、流水数据等数据,存在巨大挖掘价值[2-3]。曹景扬[4]在《ETC用户精准画像系统的研究与设计》中运用了Java语言、SpingMVC轻量级框架、Maven管理项目工具、Tomcat服务器和ETL数据仓库等技术,把ETC作为媒介,达到了统计各个关键维度会员数量,如年龄段、卡余额、车资产等属性的目的,对用户进行甄别和筛选,形成较为详尽的车主画像。戴剑军等[5]利用ETC数据计算车辆在各路段区间上的行驶速度,作为运行状态评估的基础要素。李君羡等[6]利用收费数据对高速公路收费站通行能力进行了分析。刘群等[7]利用ETC门架数据对高速公路短时交通流进行了预测。因此,ETC数据可利用价值巨大,如何利用好ETC数据来分析用户结构及特征,需要一个快捷快速的方法。
而在公路交通领域,K-means算法可以用来分析车辆的流量模式、交通拥堵情况、路段的使用情况等。通过对交通数据进行聚类分析,交通管理者可以更好地了解交通状况,采取相应的措施来改善交通流动性和减少拥堵。例如Liu等[8]就利用K-means算法来优化应急物资配送路径,利用K-means算法对需求节点进行快速聚类,得到初始划分,简化了前期的划分程序。Zhou等[9]在对新能源汽车交通密度进行统计分析的基础上,采用K-means算法模拟了新能源汽车在充电桩附近的充电情况,然后计算了充电需求的时空分布。Wang等[10]利用WiFi探针数据来收集智能手机用户的踪迹,并提取了公交用户的特征,利用K-means聚类将数据中的非公交用户筛选出来,使得其建立的OD矩阵更加可靠。刘泉宏等[11]基于K-means聚类算法与重心法来确定共享单车的回收中心选址,新的回收中心选址有回收效率高、运营成本低等优秀特点,且利用了K-means算法处理大量数据,选址精确且方便高效。蔡宇阳等[12]利用K-means分类并定义了5种出租车运营模式,通过对比不同时间划分标准下各运行模式出租车的时间、里程载客率与收入情况,分析各类出租车在各时间段的运行效益与运行特征。刘春生等[13]设计了K-means聚类算法和基于密度的噪声应用空间聚类算法相结合的两阶段聚类方法来识别驶入服务区车辆和异常行驶的车辆,再结合各车型流量占比加权的交通状态指数,从时间和空间维度分析高速公路路段交通状态。陈宝等[14]提出了一种改进K-means聚类算法与马尔科夫链结合的行驶工况构建方法,构建出时长为1 310 s的重庆城区公交车行驶工况。翟艺阳等[15]利用K-means聚类算法对交通事故分类进行交通事故划分判别。因此,利用K-means处理海量数据集,对海量数据集聚类分析,相比于传统统计方法,具有准确、快速、便捷等优势。
高速公路ETC数据具有数据量大、数据种类多、重复数据多等特点,用传统统计方法,易出现数据量过大导致数据加载不全、统计用时时间长、难以寻找聚类中心等问题。本研究通过利用K-means算法对海量数据集聚类快速并且扩展性强的特点,将K-means算法用于处理高速公路ETC海量数据集,就入口时间、出口时间、通行里程、交易金额等数据进行聚类分析,对进入高速公路的时间为区间,对该区间的用户以通行里程及速度为特征值进行聚类,并生成其中心点及聚类用户个数,分析不同时间段、不同收费里程,不同速度,高速公路的用户的显著区别,并分析可能存在的潜在问题。
1 ETC数据构成电子不停车收费(Electronic Toll Collection,ETC)是通过安装在车辆挡风玻璃上的车载电子标签(OBU)与在收费站ETC车道上的微波天线(RSU)之间进行的专用短程通讯,利用计算机联网技术进行后台结算处理,从而达到车辆通过高速公路收费站无需停车便能缴纳高速公路通行费的目的。除此之外,我国高速公路ETC主要配置还有高清车牌识别、高清摄像机,用于保证每个行车道有2套车牌识别设备覆盖,并可以用于断面车流视频监控[16]。
目前,中国高速公路ETC数据记录有200多个字段组成,其中有很大一部分字段是为了保证交易扣费的准确以及成功率设置的冗余字段[17]。根据分析需要,本研究选取入口时间、出口时间、本省通行里程这3个字段进行数据分析。本研究选取某省高速公路在2023年6月1日00 : 00 : 00至2023年6月30日23 : 59 : 59之间入站的ETC用户数据分析,约531万条数据。数据中含有因网络延迟、设备故障等原因产生的重复及异常数据,这些数据中含有重复数据以及离群数据,会对聚类结果产生不利影响,故利用Python进行数据清洗,筛取速度在30~200 km/h,行驶时间高于10 s的非重复数据,得到可用数据约为341万条数据。
2 基于K-means算法的用户聚类 2.1 K-means算法K-means聚类算法由Mac Queen J.于1967年提出,它是一种常用于聚类分析的无监督机器学习的经典算法[18]。它的主要目标是将一组数据点划分为不同的簇(Clusters),使得同一个簇内的数据点更加相似,而不同簇之间的数据点差异较大。这种算法可以帮助我们发现数据中的隐藏模式和结构,从而进行数据的分类和分组。K-means算法的基本思想是对于给定数据点xi和其所属的聚类中心cj,目标函数如下:J= 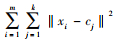

K-means算法需要预先确定出聚类数K值,若K值定的过小,则不能反映数据集的特征;若K值定得过大,虽然样本划分会更加精细,每个簇的聚合程度会逐渐提高,但对于小样本数据集,K值过大会与数据集对象个数接近,体现不出聚类的目的;对于大样本数据集,会增加计算量,延长计算时间,且容易造成过拟合现象,分析不具有普遍性。因此,可利用手肘法、轮廓系数法等方法辅助确定K值。
本研究采用手肘法确定K值,其核心指标为SSE(误差平方和),其公式为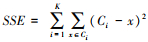
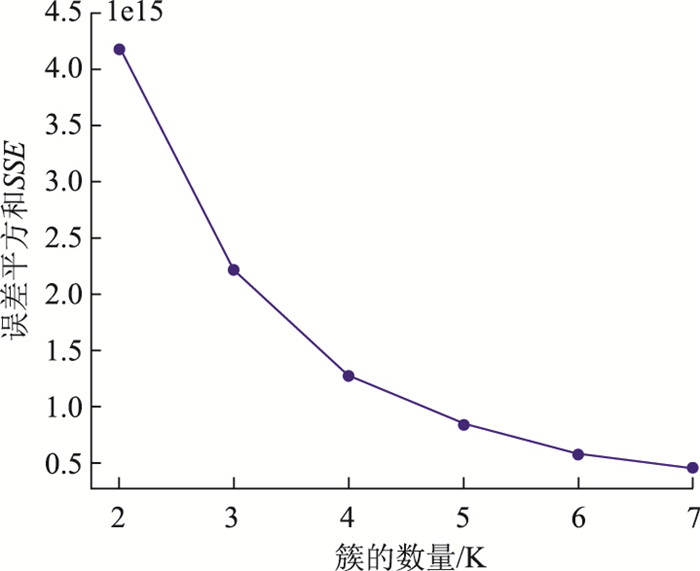
|
| 图 1 不同K值对应的SSE的手肘图(总体) Fig. 1 Overall elbow plot of SSE corresponding to different K values |
| |
令K=3并在整个数据集上以收费里程、速度、行驶时间为特征值进行K-means聚类,得到表 1数据,并根据数据标准化后画出雷达图,如图 2所示,图中簇1为在数据集中占比最高的一类,簇2为在数据集中占比第二高的一类,簇3为数据集中占比最低的一类。
| 收费里程/m | 速度/(km·h―1) | 行驶时间/h | 占比/% |
| 54 466.59 | 101.86 | 0.54 | 47.8 |
| 31 524.85 | 76.43 | 0.42 | 44.8 |
| 214 824.99 | 80.27 | 2.86 | 7.4 |

|
| 图 2 数据标准化后各簇的雷达图(总体) Fig. 2 Overall radar charts of each cluster after data standardization |
| |
从整体层面上看,该高速公路短途车占比较多,长途通行时间多为3 h左右,短途通行时间多为30 min左右,整个通行速度上面也比较快速。但是从整体层面上获取的信息还是太少,高速公路通行时段对车流量影响较大,所以本研究将用户进入高速公路的时间分为7个时间段,并建立7个数据集,分别为:进入高速时间在03 : 00 : 00-05 : 59 : 59之间的定义为清晨数据集,06 : 00 : 00-09 : 59 : 59之间的定义为早晨数据集,10 : 00 : 00-13 : 59 : 59之间的定义为中午数据集,14 : 00 : 00-16 : 59 : 59之间的定义为下午数据集,17 : 00 : 00-19 : 59 : 59之间的定义为傍晚数据集,20 : 00 : 00-22 : 59 : 59之间的定义为晚间数据集,23 : 00 : 00至次日2 : 59 : 59之间的定义为午夜数据集。在不同时间段,对不同的数据集进行K-means聚类分析,用来分析不同时间段,主要用户的变化,并分析其变化的原因。
3.2 K-means应用于入站时间通过对总体数据集进行筛选,得到早晨数据集约71.2万条数据,中午数据集约75.7万条数据,下午数据集约71.8万条数据,傍晚数据集约68.4万条数据,晚间数据集约34.2万条数据,午夜数据集约11.6万条数据,清晨数据集约7.9万条数据,对所有数据集进行K-means聚类,K=3,得到以下结果,早晨、中午、下午、傍晚、晚间、午夜、清晨的聚类中心点如表 2所示,并根据数据标准化后画出雷达图,如图 3所示,图中簇1为在数据集中占比最高的一类,簇2为在数据集中占比第二高的一类,簇3为数据集中占比最低的一类。
| 时间 | 收费里程/m | 速度/(km·h―1) | 行驶时间/h | 占比/% |
| 52 835.90 | 102.80 | 0.52 | 49.2 | |
| 早晨 | 30 203.09 | 77.79 | 0.40 | 44.4 |
| 227 657.83 | 82.05 | 2.99 | 6.4 | |
| 55 430.93 | 101.89 | 0.55 | 48.8 | |
| 中午 | 34 024.75 | 75.62 | 0.46 | 42.8 |
| 220 310.65 | 79.22 | 2.95 | 8.4 | |
| 55 718.49 | 100.98 | 0.56 | 46.5 | |
| 下午 | 31 422.87 | 76.49 | 0.42 | 44.3 |
| 200 371.34 | 82.98 | 2.54 | 9.2 | |
| 27 433.74 | 76.90 | 0.37 | 46.8 | |
| 傍晚 | 51 922.42 | 101.16 | 0.52 | 45.8 |
| 189 968.78 | 82.29 | 2.44 | 7.4 | |
| 56 541.52 | 102.19 | 0.56 | 47.0 | |
| 晚间 | 31 006.39 | 76.91 | 0.41 | 46.6 |
| 209 467.31 | 80.07 | 2.85 | 6.4 | |
| 52 322.47 | 104.28 | 0.50 | 48.7 | |
| 午夜 | 46 996.82 | 74.65 | 0.64 | 47.4 |
| 324 763.22 | 60.67 | 5.79 | 3.9 | |
| 44 086.07 | 72.63 | 0.61 | 51.3 | |
| 清晨 | 58 063.06 | 104.01 | 0.56 | 39.5 |
| 239 314.56 | 70.64 | 3.67 | 9.2 |

|
| 图 3 数据标准化后各簇的雷达图 Fig. 3 Radar charts of each cluster after data standardization |
| |
通过数据以及雷达图可以发现,大部分时间段的车流比例没有太大变化,早晨的车速相对于总体而言,速度都有不同程度的上升,是由于早晨视线逐渐变清晰,驾驶员因视野变清晰而逐渐加快了行驶速度所导致的[23],从早晨到下午的车流量,占到总体车流量的64.2%,且雷达图未见太大变化,因此,针对高速公路整体问题进行分析时,可将重点放在06 : 00 : 00-16 : 59 : 59之间进入高速公路的车辆,以减少部分计算量。在傍晚数据集中,尽管车流量从下午的71.8万减少到68.4万,然而,短途慢速车辆的比例却排在首位。尽管此时段的车流减少,但车速并未提升,表明通行效率降低。因此,若需分析影响通行效率的问题,建议着重关注在傍晚17 : 00 : 00-19 : 59 : 59进入高速公路的车辆数据。快速车辆簇组的中心点均超过104 km/h,这提示我们应警惕这一时段可能存在的超速驾驶行为。而在午夜数据集中,慢速簇组的行驶时间长达5.8 h,这也需要我们警惕可能存在的疲劳驾驶行为。
为进一步分析该高速公路的特征,根据上述聚类结果,发现在收费里程都聚类中心在60 000 m和250 000 m附近,故以此为分类依据,对收费里程进行分段聚类分析。
3.3 K-means应用于收费里程根据上述分类,将用户分为短程,中程,长程用户,定义收费里程小于60 000 m的用户为短程用户,收费里程在60 000~250 000 m之间的用户为中程用户,收费里程高于250 000 m的用户为长程用户。得到约241万条短程数据,约94万条中程数据,约6万条长程数据。将短程、中程、长程用户以速度及入站时间为特征值进行K-means聚类,根据手肘法,如图 4所示,K=4,由于时间具有周期性,在00 : 00 : 00与23 : 59 : 59这些时间点上具有相似但数字相差过大的特征,所以利用环形特征编码,将时间映射在坐标轴上,在保留周期性信息的同时,避免在最大值和最小值之间有不必要的距离。得到以下结果,短程、中程、长程聚类中心点如表 3所示,结果排序按照占比比例由大到小排列。
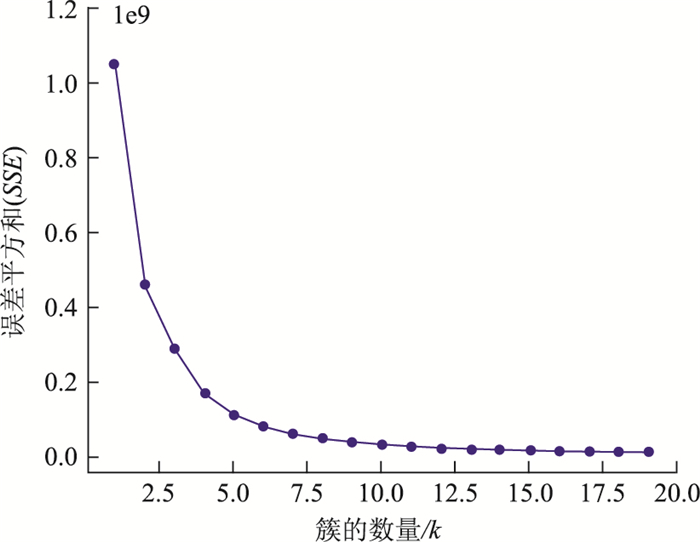
|
| 图 4 不同K值对应的SSE的手肘图(收费里程) Fig. 4 Elbow plot of charging mileage SSE for different K-values |
| |
| 里程 | 速度/ (km·h―1) |
X_encoded | Y_encoded | 入站时间 | 占比/% |
| 短程 | 88.59 | ―0.627 103 | 0.645 263 | 08:56:43 | 32.6 |
| 87.07 | 0.541 511 | ―0.661 780 | 20:37:10 | 24.7 | |
| 101.61 | ―0.561 036 | ―0.663 260 | 15:19:05 | 22.5 | |
| 72.10 | ―0.560 892 | ―0.652 551 | 15:17:16 | 20.2 | |
| 中程 | 103.43 | ―0.583 477 | ―0.687 926 | 15:18:47 | 29.0 |
| 97.32 | ―0.593 564 | 0.662 590 | 08:47:25 | 28.3 | |
| 92.06 | 0.535 626 | ―0.671 269 | 20:34:20 | 24.5 | |
| 71.32 | ―0.714 999 | ―0.349 528 | 13:44:12 | 18.2 | |
| 长程 | 87.43 | ―0.518 710 | ―0.708 525 | 15:35:10 | 33.9 |
| 57.00 | ―0.749 833 | 0.219 657 | 10:54:41 | 24.7 | |
| 91.05 | ―0.648 654 | 0.598 113 | 09:09:17 | 22.7 | |
| 64.53 | 0.631 753 | ―0.379 134 | 21:56:07 | 18.7 |
从数据中可以观察到几个明显的趋势:短程车辆主要集中在白天进入高速,速度大多集中在80~90 km/h。中程车辆的速度普遍较快,主要集中在90~100 km/h之间,进入高速的时间相对分散,但大部分中程用户和短程用户都选择在白天高速公路。长程车辆的速度通常较慢,大多数车速都不超过90 km/h,并且更倾向于在上午进入高速。需要注意的是,由于数据记录的是车辆进入和离开收费站之间的时间差,因此行驶途中进入服务区的时间也被计入其中,可能导致实际速度高于数据所显示的速度。因此,若要统计中短途用户的特征,可以着重分析白天进入高速公路的用户数据。而若想了解长途用户的特征,可以聚焦于上午高速公路的用户数据。
根据上述聚类结果,将速度也划分为3段,分别进行聚类分析,由于上述分类速度没有很明显的中位值,结合实际情况,以70 km/h和100 km/h为分界点,对速度进行分组聚类分析。
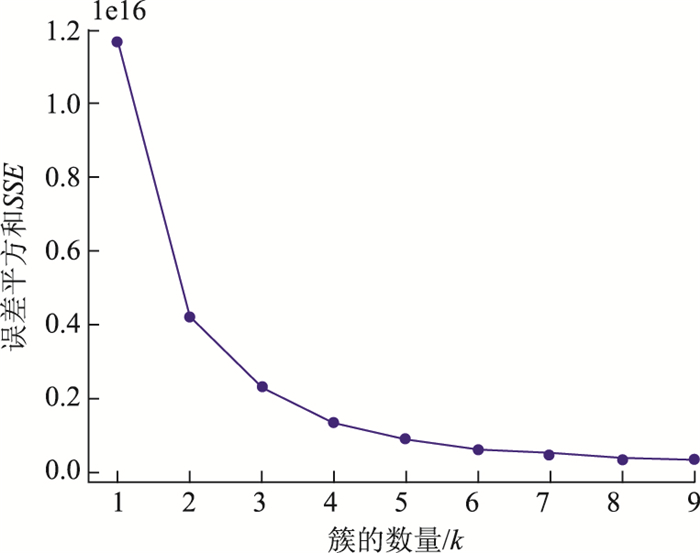
3.4 K-means应用于速度根据上述分类,将用户分为低速,中速,高速用户,定义速度小于70 km/h的用户为低速用户,70~100 km/h的用户为中速用户,高于100 km/h的用户为高速用户。得到约45万条低速数据,约215万条中速数据,约80万条高速数据。将低速、中速、高速用户以收费里程、行驶时间及入站时间为特征值进行K-means聚类,根据手肘法,如图 5所示,K=3,同样对时间进行环形特征编码,在保留周期性信息的同时,避免在最大值和最小值之间有不必要的距离。得到以下结果,低速、中速、高速聚类中心点如表 4所示,结果排序按照占比比例由大到小排列。
|
| 图 5 不同K值对应的SSE的手肘图(速度) Fig. 5 Elbow plot of velocity SSE for different K values |
| |
| 用户 | 收费里程/ m |
行驶时间/h | X_encoded | Y_encoded | 入站时间 | 占比/ % |
| 42 355.38 | 0.70 | ―0.702 209 | 0.291 517 | 10:29:49 | 46.0 | |
| 低速 | 38 939.41 | 0.64 | 0.107 616 | ―0.773 563 | 18:31:40 | 45.6 |
| 304 127.44 | 5.55 | ―0.297 784 | ―0.084 690 | 13:03:30 | 8.4 | |
| 38 165.35 | 0.44 | 0.093 679 | ―0.799 276 | 18:26:44 | 45.9 | |
| 中速 | 37 629.33 | 0.43 | ―0.732 222 | 0.285 245 | 10:34:51 | 45.3 |
| 189 524.78 | 2.24 | ―0.410 923 | ―0.239 021 | 14:00:44 | 8.8 | |
| 49 681.45 | 0.46 | ―0.700 576 | 0.334 988 | 10:17:46 | 47.3 | |
| 高速 | 50 921.94 | 0.47 | 0.171 779 | ―0.752 098 | 18:51:27 | 39.0 |
| 162 070.66 | 1.51 | ―0.419 597 | ―0.221 571 | 13:51:20 | 13.7 |
短途低速车辆中占比最高的并非长途车辆,而是在行程大约40 km左右的短途车辆,这出乎预料。若要探其原因,可借助车型和运载货物数据,进行特征值分析。对于中速车辆,收费里程在中短途间变化不大,但入站时间分布在上午和下午,这推出存在大量通勤车辆。若想分析通勤车辆,应利用通行次数,筛选出在这个车速区间的车辆,进一步深入分析。高速车辆与中速车辆相似,收费里程和入站时间也相近,同样存在大量通勤车辆。总体而言,高速和中速车辆的收费里程偏向中短途,而低速车辆的收费里程则更偏向长途,这些发现能为进一步分析提供重要线索。
本研究主要聚焦于速度、收费里程和行驶时间进行了聚类分析,从进站时间、行驶里程和速度等方面分析了不同用户的特征变化,并尝试探讨了潜在的问题。然而,要对特定情况进行更深入的分析,需要借助更多的ETC数据特征值。此外,利用门架数据能够获取更精确的速度变化情况,进一步完善分析。整体而言,结合更多数据特征和门架数据将有助于全面理解用户行为和问题根源。
4 结论综上所述,K-means算法是一种可以在短时间处理大量数据并且聚类的算法,对于ETC数据集这种大量数据,有良好的实用性,相比于传统统计方法,K-means算法可以快速高效处理数据量更大、数据字符更多、时间跨度更长的数据集,还可以使指定时间段的特征值可视化,使得分析不同日期的指定时间段更加直观。随着差异化政策的施行,虽然有效实现了“降本增效”、“引车上路”,进而实现高速公路用户与高速公路公司的双赢,但中国目前仍然存在区域发展不平衡、不充分现象,各省区域路网发展状况及其交通流特征与运输需求也差异较大,各省高速公路收费费率体系与标准也不尽相同。通过K-means算法,可以快速精确处理大量用户通行数据,并提取出该路段(路网)的交通流特征及主要用户,针对不同地区的不同情况,分析其主要用户的特征。例如在有特色服务区的高速公路中,可以利用K-means算法统计并比较节假日及工作日的主要车速、车型及进入高速公路时间等信息,制订更加精细化的差异化收费政策,例如对节假日采取预约制差异化收费,针对进入高速公路时间的聚类中心点,分析出其高峰时间段与低谷时间段,对高速公路高峰时间段采取预约制进入,对未提前预约车辆适当增加部分车费,对进入高速公路低谷时间段采取提前预约适当减免的优惠政策,达到“削峰平谷”的目的,使高峰时段的用户享受较高的道路服务水平,使低谷时间段的用户享受到适量的优惠,使高速公路公司与每个用户都能实现更大的双赢,进一步提升“降本增效”、“引车上路”效果。
| [1] |
陈维翰. ETC技术之后的我国智慧高速公路发展问题探讨[J]. 中国交通信息化, 2020, 22(4): 90-92. CHEN Wei-han. Discussion on the Development of China 's Smart Expressway after ETC Technology[J]. China ITS Journal, 2020, 22(4): 90-92. |
| [2] |
刘群, 杨濯丞, 蔡蕾. 基于ETC门架数据的高速公路短时交通流预测[J]. 公路交通科技, 2022, 39(4): 123-130. LIU Qun, YANG Zhuo-cheng, CAI Lei. Predicting Short-term Traffic Flow on Expressway Based on ETC Gantry System Data[J]. Journal of Highway and Transportation Research and Development, 2022, 39(4): 123-130. DOI:10.3969/j.issn.1002-0268.2022.04.014 |
| [3] |
马春平. 基于全国联网ETC运营数据的应用研究[D]. 北京: 北京邮电大学, 2018. MA Chun-ping. Application Research Based on ETC Operational Data in National Network [D]. Beijing: Beijing University of Posts and Telecommunications, 2018. |
| [4] |
曹景扬. ETC用户精准画像系统的研究与设计[D]. 长春: 长春工业大学, 2020. CAO Jing-yang. Research and Analysis of ETC User Precision Portrait System[D]. Changchun: Changchun University of Technology, 2020. |
| [5] |
戴剑军, 李天豪, 李苗华, 等. 基于收费数据的高速公路路网运行状态评估方法研究[J]. 公路工程, 2023, 48(4): 158-166. DAI Jian-jun, LI Tian-hao, LI Miao-hua, et al. Evaluation Method of Expressway Network Running State Based on Toll Data[J]. Highway Engineering, 2023, 48(4): 158-166. |
| [6] |
李君羡, 周一晨, 高志波, 等. 基于收费数据的高速公路收费站通行能力分析[J]. 公路交通科技, 2021, 38(11): 106-116, 125. LI Jun-xian, ZHOU Yi-chen, GAO Zhi-bo, et al. Analysis on Capacity of Expressway Toll Station Based on Toll Data[J]. Journal of Highway and Transportation Research and Development, 2021, 38(11): 106-116, 125. DOI:10.3969/j.issn.1002-0268.2021.11.013 |
| [7] |
刘群, 杨濯丞, 蔡蕾. 基于ETC门架数据的高速公路短时交通流预测[J]. 公路交通科技, 2022, 39(4): 123-130. LIU Qun, YANG Zhuo-cheng, CAI Lei. Predicting Short-term Traffic Flow on Expressway Based on ETC Gantry System Data[J]. Journal of Highway and Transportation Research and Development, 2022, 39(4): 123-130. DOI:10.3969/j.issn.1002-0268.2022.04.014 |
| [8] |
LIU C, YU J J, HAN S X, et al. Research on the Optimization of Emergency Material Distribution Route in "Vehicle" Mode Based on K-Means Clustering and LK Algorithm[J].
Journal of Web Systems and Applications, 2022, 4(1): 11-18.
|
| [9] |
ZHOU J X, WANG R X, HUANH W J, et al. Location and Layout of Electric Vehicle Charging Stations Based on K-Means Algorithm[J].
Journal of Physics: Conference Series, 2023, 2592(1): 1-16.
|
| [10] |
WANG Y S, ZHANG W B, TANG T L, et al. Bus OD Matrix Reconstruction Based on Clustering Wi-Fi Rrobe Data[J].
Transportmetrica B: Transport Dynamics, 2022, 10(1): 1-16.
|
| [11] |
刘泉宏, 唐福星. 基于K-means聚类算法与重心法的故障共享单车回收中心选址优化[J]. 运筹与管理, 2023, 32(7): 85-91. LIU Quan-hong, TANG Fu-xing. The Site Selection Optimization on the Recycling Center of Faulted Shared Bicycles Based on K-means Clustering Algorithm and Center of Gravity Methods[J]. Operations Research and Management Science, 2023, 32(7): 85-91. |
| [12] |
蔡宇阳, 李伯钊, 牛彦芬, 等. 基于轨迹数据的出租车运行模式识别及效益分析[J]. 测绘地理信息, 2023, 48(4): 146-150. CAI Yu-yang, LI Bo-zhao, NIU Yan-fen, et al. Identification of Taxi Operation Patterns and Benefit Analysis Based on Trajectory Data[J]. Journal of Geomatics, 2023, 48(4): 146-150. |
| [13] |
刘春生, 曹蓉, 王晓晗, 等. 基于门架数据的高速公路运行状态评价研究[J]. 山东科学, 2023, 36(3): 100-107. LIU Chun-sheng, CAO Rong, WANG Xiao-han, et al. Exploring the Traffic State Identification of Highway Based on Gantry Data[J]. Shandong Science, 2023, 36(3): 100-107. |
| [14] |
陈宝, 谢光毅, 黄春, 等. 基于改进K均值和马尔科夫链的公交车行驶工况构建[J]. 重庆工商大学学报(自然科学版), 2024, 41(3): 18-25. CHEN Bao, XIE Guang-yi, HUANG Chun, et al. Construction of Bus Driving Cycle based on Improved K-means and Markov Chains[J]. Journal of Chongqing Technology and Business University(Natural Science Edition), 2024, 41(3): 18-25. |
| [15] |
翟艺阳, 罗昱伟, 张驰, 等. 基于收费站数据的交通事故态势感知判别[J]. 公路交通科技, 2023, 40(5): 211-220. ZHAI Yi-yang, LUO Yu-wei, ZHANG Chi, et al. Awareness Discrimination of Traffic Accident Situation Based on Toll Station Data[J]. Journal of Highway and Transportation Research and Development, 2023, 40(5): 211-220. DOI:10.3969/j.issn.1002-0268.2023.05.028 |
| [16] |
刘伯海. 沈海线福泉高速公路ETC门架系统[J]. 中国交通信息化, 2019(10): 91-93. LIU Bo-hai. ETC Gantry System for the Fuquan Expressway on the Shenhai Line[J]. China ITS Journal, 2019(10): 91-93. |
| [17] |
高潮. 高速公路ETC系统数据挖掘与收费系统优化[J]. 科技风, 2023, 36(5): 61-64. GAO Chao. ETC System Data Analysis and High-Speed Road Toll Collection System Optimization[J]. KE JI FENG, 2023, 36(5): 61-64. |
| [18] |
贾瑞玉, 李玉功. 类簇数目和初始中心点自确定的K-means算法[J]. 计算机工程与应用, 2018, 54(7): 152-158. JIA Rui-yu, LI Yu-gong. K-means Algorithm of Clustering Number and Centers Self-determination[J]. Computer Engineering and Applications, 2018, 54(7): 152-158. |
| [19] |
蒋丽, 薛善良. 优化初始聚类中心及确定K值的K-means算法[J]. 计算机与数字工程, 2018, 46(1): 21-24, 113. JIANG Li, XUE Shan-liang. A K-means Algorithm Based on Optimizing the Initial Clustering Center and Determining the K Value[J]. Computer & Digital Engineering, 2018, 46(1): 21-24, 113. |
| [20] |
杨俊闯, 赵超. K-Means聚类算法研究综述[J]. 计算机工程与应用, 2019, 55(23): 7-14, 63. YANG Jun-chuang, ZHAO Chao. Survey on K-Means Clustering Algorithm[J]. Computer Engineering and Applications, 2019, 55(23): 7-14, 63. |
| [21] |
吴志敏, 黄觉, 向崎. 基于K-Means聚类算法的高速公路事故多发路段鉴别[J]. 中外公路, 2022, 42(6): 260-264. WU Zhi-min, HUANG Jue, XIANG Qi. Identification of Freeway Accident-Prone Sections Based on K-Means Clustering Algorithm[J]. Journal of China & Foreign Highway, 2022, 42(6): 260-264. |
| [22] |
王建仁, 马鑫, 段刚龙. 改进的K-means聚类k值选择算法[J]. 计算机工程与应用, 2019, 55(8): 27-33. WANG Jian-ren, MA Xin, DUAN Gang-long. Improved K-means Clustering K-value Selection Algorithm[J]. Computer Engineering and Applications, 2019, 55(8): 27-33. |
| [23] |
郭应时, 付锐, 袁伟, 等. 通道宽度对驾驶员动态视觉和操作行为的影响[J]. 中国公路学报, 2006, 19(5): 83-87. GUO Ying-shi, FU Rui, YUAN Wei, et al. Influences of Passage Width on Driver 's Dynamic Vision and Operation Behavior[J]. China Journal of Highway and Transport, 2006, 19(5): 83-87. |
 2024, Vol. 41
2024, Vol. 41


 ,
,