扩展功能
文章信息
- 雷斌, 李佳璐, 张鹏, 李微, 陈晨.
- LEI Bin, LI Jia-lu, ZHANG Peng, LI Wei, CHEN Chen
- 基于多图时空图卷积模型的城市交通流长时预测
- Long Term Prediction on Urban Traffic Flow Based on Multi-source Spatio-temporal Graph Convolutional Neural Network Model
- 公路交通科技, 2024, 41(4): 204-213
- Journal of Highway and Transportation Research and Denelopment, 2024, 41(4): 204-213
- 10.3969/j.issn.1002-0268.2024.04.021
-
文章历史
- 收稿日期: 2023-09-19
2. 中国电力工程顾问集团中南电力设计院有限公司, 湖北 武汉 430071;
3. 中建丝路建设投资有限公司, 陕西 西安 710061
2. Central Southern China Electric Power Design Institute Co., Ltd. of China Power Engineering Consulting Group, Wuhan, Hubei 430071, China;
3. China Construction Silk Road Construction Investment Co., Ltd, Xi'an, Shaanxi 710061, China
交通流预测是智能交通系统的重要组成部分,在城市交通控制和发展中起着重要的作用。交通流预测方法经历了不同的发展阶段。
传统的统计学方法最先被应用于交通流预测,如HA和ARIMA模型,通过分析历史交通数据中的模式和趋势,预测未来交通流的变化趋势[1-2]。由于交通流高度的非线性和动态性特征,这些方法往往难以准确捕捉复杂的交通流动态变化。传统的机器学习方法如支持向量机、K最近邻[3]可以对非线性交通流进行建模,并提取交通数据中更复杂的相关性。但在大数据场景中这些模型的浅层架构、手动特征选择和分离学习的结果不能令人满意。随着深度学习技术的发展,许多深度学习模型被广泛用于交通流预测任务,其中包括循环神经网络(RNN)[4]及其变种模型如LSTM、GRU[5-6]等。这些方法通过深度神经网络对交通流数据进行建模和学习,能够捕捉交通流复杂的时间相关性,从而提高预测的准确性和精度。一些研究将传统方法与新兴机器学习方向混合,例如Pan等[7]提出一种将流量模型与深度学习建模相结合的混合框架(TFMDL),它可以更好地捕捉拥挤条件下的动态交通流状态。Cui等[8]提出一种使用极限学习机来学习交通流序列内部非线性关系的混合模型(GSA-ELM),它采用引力搜索算法对极限学习机的参数进行全局优化。Hou等[9]提出一种将ARIMA和非线性小波神经网络(WNN)方法混合的模型,通过模糊逻辑对两个单独模型的输出进行分析和组合,并将加权结果作为混合模型的最终预测交通量,皆在不同程度上提高了预测的准确性。从交通流的空间相关性出发,一些研究提出了基于RNNs[10]和CNN[11]模型进行交通流预测,RNNs对交通流的时间相关性进行建模,CNN通过使用栅格化处理对路网空间性关系进行建模[12]。然而,许多交通网络在本质上是图结构的,例如道路网和地铁网,CNN不能很好地表征路网的拓扑结构。
图神经网络(GNN)模型[13]在交通流预测问题中对时间和空间相关性的建模有较直观的呈现,其能处理较为复杂的非线性关系数据。贺文武等[14]建立了一种基于双向自适应门控图卷积网络的交通流预测模型,它能够处理交通流数据缺失、异常或噪声问题。Zhao等[15]提出了时间图卷积网络(T-GCN)模型,它结合了图卷积网络(GCN)和门控递归单元(GRU),可从交通流数据中获得时空相关性。Zhu等[16]提出了属性增强时空图卷积网络(AST-GCN)模型,设计了一个属性增强单元编码和集成到时空图卷积模型的因素,引入外部因素可以提高预测交通的时空准确性。Liao等[17]集成了基于LSTM的编码器,编码了外部信息并将多模态数据建模为序列输入。Zhang等[18]提出的模型主要基于GRU模型,将交通流特征和天气信息的特征融合,实现了具有外部天气信息的交通流预测任务。Yu等[19]提出时空图卷积网络(STGCN)模型,使用一维CNN对时间动态相关性进行建模,通过GCN获取路网的局部空间相关性。以上模型在预测性能上有所提升,但仍存在以下不足:
(1) 现有研究大多只考虑了交通流数据的时间相关性,而忽略了道路节点之间的相互影响。交通流的空间相关性是指道路节点的交通状态会受到周围节点的影响,并且即使节点间空间距离相近,它们交通状态也可能存在差异。
(2) 交通流预测的核心是对交通流数据中的时间依赖和空间依赖关系进行建模。在城市路网当中,准确的交通流预测不仅依赖于历史交通流数据和路网结构,还需要考虑各种外部因素的影响,比如POI分布、天气状况等。如何对外部因素进行有效建模,是城市路网交通流预测面临的重要问题。
因此,本研究针对城市路网交通流预测任务,提出了多图时空图卷积网络模型,综合考虑时间和空间相关性,并且将外部因素有效融合到预测模型中,以提高城市路网交通流的预测精度。
1 模型建立 1.1 定义交通流预测的目标是根据历史状态和辅助信息预测未来的交通状态。虽然路段的交通状态主要由交通量、速度和密度来描述,但本研究增加了对交通流的外部影响因素的考虑。因此,本研究的交通流预测任务主要是根据城市路网节点之间的影响以及外部因素来预测路网未来一段时间内的交通流。以下定义了描述交通流的因素。
定义1:路网节点的邻接矩阵A。使用道路节点网络A =(Ad,As,Ac)来表示路段之间的连接关系。其中Ad为距离矩阵;As为功能相似性矩阵;Ac为连通性矩阵。
定义2:交通特征矩阵X。本研究中,交通量、速度、密度被视为城市道路网络上的每个节点的固有属性,由矩阵X表示,而Xit为在时间t的第i个路段上的交通特征。
定义3:融合了外部因素的特征矩阵E。Et=[Xt,Dt,S],Xt为t时刻路网所有节点的交通流特征;Dt为t时刻路网所有节点的动态因素;S为路网所有节点的静态因素。
综上所述,交通流预测问题可以理解为在路网节点的邻接矩阵A、特征矩阵X和融合了外部因素的特征矩阵E的基础上建立函数f,得到未来时段T的交通信息,如式(1)所示:

|
(1) |
纳入模型的多源因素选择是开发准确可靠的交通流预测模型的关键步骤。这一选择应该基于对交通流潜在机制的理解,以及对数据的可用性和质量的考量。本研究根据现有研究,将影响交通流的外部因素分为以下两大类,具体如下:
(1) 静态因素:是不随时间变化的特征,可提供有关道路网络和交通需求的稳定、长期信息。静态因素可从影响范围角度分为宏观性和微观性。本研究将土地利用性质作为宏观角度,来提供可能在该地区产生交通活动和目的地类型的信息,将道路POI分布位置和集中度作为微观角度来影响某个路网节点的交通流模式和特征;道路宽度、车道数同样作为微观角度来影响具体节点的通行能力等。通过将这些静态因素纳入交通流预测模型,可以捕捉城市规划和发展对交通流模式的长期影响。
(2) 动态因素:是随时间变化的特征,会对交通流产生短期且重大的影响。本研究从影响方式和机理角度,将动态因素分为两类,即周期性和随机性动态因素。周期性动态因素是指例如早晚高峰等表现出规律性和可预测模式的外部因素,随机性动态因素是指例如交通事故、天气等具有随机性且会对交通流产生显著影响的因素。本研究的外部因素分类如图 1所示。

|
| 图 1 影响城市交通流的外部因素分类 Fig. 1 Classification of external factors affecting urban traffic flow |
| |
除了本研究考虑的因素外,其他附加的外部因素也可能会影响交通流。因此,这种分类为未来的研究提供了基础,以扩展和进一步探索多源因素在交通流预测中的作用,提高预测模型的可解释性。
1.3 模型框架融合多源数据的多图时空图卷积网(Multi-source Spatio-temporal Graph Convolutional Neural Network,MSGCNN) 的模型框架如图 2所示,模型主要由4部分构成:基于多源数据的多图构造,利用不同类型的数据生成不同视角的邻接矩阵,包括距离矩阵、功能相似矩阵和连通性矩阵,表征路网的空间相关性;再基于门控循环单元(GRU)的时间相关性建模,捕捉交通流数据的动态变化和周期性规律;以及基于图卷积网络(GCN)的空间相关性建模,学习节点特征和邻接信息;最后构建一个数据融合层,将多视角邻接矩阵和时空特征结合起来,使用单层全连接神经网络将未来动态因素映射到未来时段输出的交通流特征维度, 相同后再输出预测结果。

|
| 图 2 MSGCNN模型框架 Fig. 2 MSGCNN model framework |
| |
1.4 多源数据融合
前文已经分析了两类静态因素和两类动态因素对交通流的影响,此处对输入模型的动态因素和静态因素进行具体定义和维度说明,如表 1所示。
| 外部因素 | 类别数量 | 向量维度 | 变量类型 | 数据说明 | |
| 动态因素 | 是否节假日 | 2 | 1 | 0-1变量 | 时段信息矩阵 |
| 是否周内 | 2 | 1 | 0-1变量 | ||
| 是否周末 | 2 | 1 | 0-1变量 | ||
| 是否属于早晚高峰时段 | 2 | 1 | 0-1变量 | ||
| 天气 | 4 | 4 | One-Hot变量 | 天气信息矩阵 | |
| 静态因素 | POI分布 | 9 | 9 | 路段9种POI的数量分布 | POI信息矩阵 |
| 用地类型 | 3 | 3 | One-Hot变量 | 用地类型信息矩阵 |
由表 1可知,动态因素共分为2类,总维度为8;静态因素分为2类,总维度为12。由于静态因素S不随时间变化,动态因素D随时间变化,定义t时刻融合了多源数据的交通流特征为Et:

|
(2) |
式中,Xt∈Rn为t时刻路网所有节点的交通流特征;Dt∈Rn×m为t时刻路网所有节点的外部动态因素;S ∈Rn×d为路网所有节点的外部静态因素;Et∈Rn×(m+d)为t时刻融合了多源数据路网交通流特征矩阵。
使用外部因素构建不同视角下的邻接矩阵, 这种方法减少了特征空间的维度,允许模型通过邻接矩阵捕获外部因素与交通流之间的复杂关系,显著降低了模型的复杂度和内存需求,已经证明可以提高城市道路网络中交通流预测的准确性和可靠性[20]。
1.4.1 多源数据的邻接矩阵构造邻接矩阵是图数据的基本表示之一,用于定义图中节点之间的连接关系,为建模图中节点之间的关系提供了手段,使得网络能够有效地学习特征表示并考虑图数据之间的复杂和非线性关系。因此在考虑静态因素的基础上,从邻近性、功能相似性、连通性3个角度构造多视角邻接矩阵来表征路网的空间相关性,具体如下:
(1) 距离矩阵
在路网当中,即使是邻接节点,由于节点之间距离的不同,其相关性也会变化,距离越小其相关性越强,而随着距离的增大其相关性会减弱。此处按照此文献[21]的方法构造基于高斯核函数的距离矩阵Ad,表示如下:

|
(3) |
式中,aij为基于高斯核函数构造的距离矩阵的第i行第j列的值;dij为路网节点i与j之间的距离;ε,σ2为超参数,控制矩阵分布和稀疏性的阈值。
(2) 功能相似性矩阵
功能相似性矩阵As∈ Rn×n可以用节点周边的POI分布向量的相似度来度量,则功能相似度矩阵As表示如下:

|
(4) |
式中,As (i, j)为功能相似性矩阵As中的第i行第j列的元素,即节点i和节点j的功能相似大小,其取值范围为As (i, j)∈[0, 1];Pvi,Pvj为路网节点i和节点j的静态因素向量,即静态因素矩阵S的第i行和第j列。
(3) 连通性矩阵
连通性是指虽然两节点之间没有直接相连,但是经过K个节点之后,两节点之间存在路径,则认为两个节点之间是连通的。尽管在严格的路网邻接矩阵当中两节点没有直接相连,但在现实中,属于同一路径当中的道路交通流往往也具有很强的相关性,因此定义连通性矩阵Ac:

|
(5) |
式中,Ac(i, j)为连通性矩阵Ac中的第i行第j列的元素,若为1则代表两节点连通,若为0则代表不连通;conn(vi, vj)K为连通性函数,若节点i和节点j在K个节点之内存在路径,则取值为1,否则为0;Ai, j为路网原始邻接矩阵,若节点i和节点j为相邻节点则为1,否则为0;max(·)代表取最大值,此处除去一阶连接,只保留一阶以及以上连接。
1.5 时空相关性建模 1.5.1 基于图卷积网络的空间相关性建模模块本研究使用图卷积网络,因其能够捕捉图的拓扑和空间依赖性,实现对图数据的特征表示和预测的有效学习,被广泛用于交通流预测任务。
一般情况下GCN的输入包含两部分,一部分是路网的邻接矩阵A,一部分为历史交通流特征矩阵X,则叠加多层GCN可表达为:

|
(6) |
式中,


本研究在原始邻接矩阵的基础上融入了路网节点当中的静态因素,构造了Ad,As和Ac,此处使用融入静态因素的邻接矩阵代替A。此处以及后文均以距离邻接矩阵Ad为例说明,两层的图卷积可表示为:

|
(7) |
式中,W0∈ Rm×H,W1∈ RH×T分别为第1层、第2层图卷积的权重矩阵;H为隐藏层单元数;m为输入序列的特征数量;

门控循环单元是RNN的一个扩展模型。一般来说,GRU与LSTM, RNN相比具有更易于训练,且效果更好的优势,因此被广泛用在时序建模当中。本研究使用GRU对城市路网交通流的时间相关性进行建模。GRU利用更新门Zt和重置门Rt来控制信息的存取与遗忘,在得到图卷积网络的输出gc(X,Ad)之后,将它代入到门控循环单元之中,此处仅以距离邻接矩阵Ad单通道进行说明,表示如下:

|
(8) |

|
(9) |

|
(10) |

|
(11) |

|
(12) |
式中,gc(·)为图卷积过程;Xt为t时刻路网所有节点的交通流特征;Wxr,Whr,Wxz,Whz均为权重参数;br,bz,bh,bt均为偏置项;
当得到3个通道的输出之后,对结果进行融合,即得到基于静态因素的结果,表示如下:

|
(13) |
式中,


由于待预测时段中的动态因素有部分是可预知的,例如是否为节假日、是否为周内、是否属于早晚高峰时段,而天气信息可以通过天气预报等渠道提前获取。因此,在输出最终预测结果时,可以将待预测时段对应的动态信息融入到网络模型中进行训练,并将动态因素矩阵映射到与预测结果相同的维度进行融合。这样,最终的预测结果可以表示为:

|
(14) |

|
(15) |
式中,y2为将动态因素映射到与预测输出相同的维度后的矩阵;De为基于动态因素的预测后果;We,W1,W2为权重参数;be,b为偏置项;y为最终的预测输出。
2 试验结果与分析 2.1 数据集说明SZ-TAXI:该数据集由2015年1月1日至1月31日深圳市部分地区大约15 000辆出租车的轨迹数据组成,选择了罗湖区156条主干道作为主要研究区域。试验数据包含两部分:一是描述路网道路关系的156×156的邻接矩阵,其中数值为1则代表道路间连通;二是大小为2 976×156交通速度矩阵,记录了每条道路上的交通速度随时间的变化,其中每一行代表一个时间节点路网所有路段的交通速度,每一列代表一条道路的历史交通速度[22]。
用地类型信息矩阵:由于不同用地性质下的交通模式存在明显区别,因此根据本数据集所涉及区域的具体情况,将用地类型分为3类:工业用地、居住用地和商业服务业设施用地,以此构造三维的One-Hot编码向量,形成大小为156×3的用地类型信息矩阵。后续若将该模型应用于其他区域的交通流预测任务,可根据实际需要增加用地类型,构造用地信息矩阵。
POI信息矩阵:本研究结合实际情况,参考高德地图POI分类体系,重新构建分类体系。POI类别可分为9种类型:餐饮服务、企业、购物服务、交通设施、教育服务、生活服务、医疗服务、住宿等。本研究利用网络爬虫技术获取该数据集所对应道路周边的POI信息,包括POI的数量、类型和位置信息。然后将POI按照以上9种类型的一级类别进行分类,最后统计出该数据集中156个路段对应的9种POI的数量信息,并构建一个156×9的POI信息矩阵。后续研究者可根据预测场景和需求重新构造POI信息矩阵。
时段信息矩阵:时段因素的字段包含是否高峰时段、是否周内、是否周末、是否节假日4个字段。若属于该时段则对应变量值为1,否则为0。SZ-TAXI数据集提供了2 976条交通速度数据所对应的时间信息,根据该数据集所提供的时间,构造对应大小为2 976×4的时段信息矩阵。
天气信息矩阵:本研究利用网络爬虫技术获取该路网所在区的历史天气数据。为了与历史交通流数据一致,本研究以15 min的时间间隔统计了天气信息。根据实际情况和建模需要以及每个类别对驾驶员行为、道路条件等对城市交通流的影响程度进行了分类,并对33种天气类型进行了重新归类,如表 2所示。
| 一级分类 | 二级分类 |
| 无影响 | 晴天、多云、阴天 |
| 低影响 | 阵雨、雨夹雪、小雨、小雪、浮尘、扬沙、小雨-中雨、小雪-中雪、冻雨 |
| 中等影响 | 中雨、大雨、中雨-大雨、阵雪、中雪、大雪、冻雨、中雨-大雨、中雪-大雪、雷阵雨、雾、霾 |
| 高影响 | 雷暴、雷阵雨伴有冰雹、大雨-暴雨、暴雨-大暴雨、大暴雨-特大暴雨、沙尘暴、强沙尘暴、大雪-暴雪、特大暴雨 |
最后,根据这4个类别构造了四维的One-Hot编码向量,用以表征天气状况,形成大小为2 976×4的天气信息矩阵。
2.2 对比模型本研究使用7种模型进行对比试验:
(1) HA用于分析时间序列数据并预测未来值的基准模型,因其较低的复杂度和较快的计算速度,通常与其他复杂的预测模型进行比较。
(2) ARIMA能够对非平稳的时间序列进行建模和预测,通过对时间序列数据进行差分处理,使其趋于平稳,然后利用序列自身的历史信息和残差项来建模并预测未来值。
(3) SVR是一种机器学习模型,可以预测连续值的数据,它通常被用来预测道路交通流的变化情况。
(4) LSTM可以在处理时序数据时保留长期依赖性,通过门结构控制,能更好地处理时间序列的预测任务。
(5) GRU同样通过门结构控制,能够记忆长时间间隔内的信息,有较好的预测精度。
(6) 在T-GCN中,GCN用于捕获交通流的空间相关性,GRU用于捕获时间相关性,T-GCN可以通过获取交通数据的时空相关性预测城市路网交通流。
(7) DCRNN通过对交通网络图进行建模,结合循环神经网络和扩散卷积来建模交通流的流入和流出关系,利用历史交通数据对每条道路的交通流状态进行预测。
HA,ARIMA和SVR属于传统的交通流预测模型,主要关注交通流数据之间的时间相关性。LSTM和GRU能够捕获时间序列数据中的长期时间依赖性来提高预测精度。T-GCN和DCRNN同时考虑了时间相关性和空间相关性,能够对交通流数据的时空相关性建模。
2.3 参数设置本研究试验平台CPU采用Intel Xeon(R)Platinum 8259CLCPU@2.50GHz,GPU采用NVIDIA Tesla T4图形卡,使用Python3.9和PyTorch1.10实现本研究模型。模型的初始学习率为0.01,最小学习率为5.0×10―5,从第20轮训练之后开始每10轮减少10%,批量大小为16。
试验过程中,对数据集进行Z-score归一化操作,并将数据集分为80%的训练集和20%的测试集。以SZ-TAXI数据集为例说明,历史序列长度在[4, 6, 8, 12, 16, 20]中进行测试,隐藏层单元数量从[8, 16, 32, 64, 100, 128]选择。试验结果如图 3所示,其中纵轴表示不同长度对应的RMSE和MAE精度,横轴代表不同的参数选择。图 3(a)显示了模型精度随不同历史序列长度的变化情况。当历史序列长度为12时,模型表现最佳,而且精度随着序列长度的增加而降低,因此选择序列长度12。图 3(b)显示了取不同隐藏层单元数量时对应的精度,当隐藏层单元数量为32时,其性能最佳。因此,最终确定在SZ-TAXI数据集中,历史序列长度为12,隐藏层单元的数量为32。

|
| 图 3 SZ-TAXI数据集不同超参数下模型性能 Fig. 3 Model performance with different hyperparameters in SZ-TAXI dataset |
| |
2.4 评价指标
平均绝对误差(Mean Absolute Error,简称MAE)是评价回归模型最基本的指标,直观反映了模型预测值与真实值之间的误差,MAE的值越低,表明模型的性能越好。均方根误差(Root Mean Squared Error,简称RMSE)在均方误差的基础上做了平方根来衡量预测值和真实值之间的偏差,因此RMSE会将模型预测结果中较大的误差放大, 其值越小模型效果越好。试验选取平均绝对误差、均方根误差这两个常用评价指标。具体计算公式如下。
(1) 平均绝对误差MAE

|
(16) |
(2) 均方根误差RMSE

|
(17) |
式中,yij和
本试验使用SZ-TAXI数据集,分别在15,30 min和60 min预测时间长度上测试模型的性能,如表 3所示。
| 数据集 | 预测时长/min | 指标 | HA | ARIMA | SVR | LSTM | GRU | T GCN | DCRNN | MSGCNN |
| SZ-TAXI | 15 | RMSE | 4.29 | 7.24 | 4.84 | 3.99 | 3.96 | 3.92 | 4.03 | 3.90 |
| MAE | 2.78 | 4.98 | 3.04 | 2.81 | 2.78 | 2.71 | 2.70 | 2.56 | ||
| 30 | RMSE | 4.29 | 6.78 | 4.96 | 4.09 | 3.99 | 3.96 | 4.05 | 3.95 | |
| MAE | 2.78 | 4.67 | 3.28 | 2.69 | 2.77 | 2.73 | 2.73 | 2.64 | ||
| 60 | RMSE | 4.29 | 6.77 | 5.21 | 4.07 | 4.10 | 4.00 | 4.10 | 3.99 | |
| MAE | 2.78 | 4.66 | 3.51 | 2.93 | 2.91 | 2.88 | 2.85 | 2.74 |
同时为了更好地说明MSGCNN模型的预测性能,本研究选取了SZ-TAXI数据集中的一条道路进行可视化分析,本研究将从以下几个角度进行分析。
(1) 预测性能:基于深度学习的方法(LSTM,GRU,T-GCN,DCRNN)比传统方法具有更高的准确性。与SVR和ARIMA相比,MSGCNN的RMSE在15 min预测尺度上分别降低了46.13%和19.42%,MAE分别降低了48.59%和15.79%。随着预测时间的增加,模型的提升有所降低,但无论与传统模型还是深度学习模型相比,仍然有所提升。在较长的60 min预测尺度上,与LSTM,GRU,T-GCN和DCRNN相比,MAE分别提高了6.48%,5.84%,4.86%和3.80%。
(2) 时间滞后现象:通过观察图 4,预测结果存在一定时间滞后现象,随着预测时间的增加,滞后现象更加明显,60 min长度的滞后情况最为明显。时间滞后性的产生可能是在训练模型时使用的训练数据中包含时间信息,模型就会学习到时间的相关规律,并将其用于输出的预测。本研究推测,由于SZ-TAXI数据集较小,因此训练出来的模型泛化能力较差,如果采用涵盖更多数据的数据集进行试验,滞后现象会有所缓解。

|
| 图 4 MSGCNN预测结果可视化 Fig. 4 Visualization of MSGCNN prediction results |
| |
(3) 交通流突变点的捕捉:对于速度变化拐点的捕捉,MSGCNN模型存在偏差,并且随着预测步长的增大更加突出。本研究分析交通流的突变是对交通环境的综合影响,如果能在模型中引入更多的动态因素,如交通事故、社会事件等因素,这个问题会得到更好的解决。
2.5.2 消融试验为了验证MSGCNN模型静态特征编码的多图,以及动态特征的融合对模型的贡献,本研究设计了消融试验来进行验证。消融试验设置如下。
(1) 消融模型1:验证融合多源数据对模型的贡献,不使用任何外部因素,也不使用多图融合,仅使用原始的0和1组成邻接矩阵,也不保留最后的动态因素融合层。
(2) 消融模型2:验证静态因素模型的贡献,即仅使用动态因素而不使用静态因素,不使用多图融合,仅保留最后的动态融合层。
(3) 消融模型3:验证动态外部因素模型的贡献,即使用完整的静态因素,保留多图融合,但不使用最后的动态因素融合。
(4) MSGCNN:同时使用动态和静态因素下的模型性能,即使用原始模型。
通过消融试验表 5中的结果进行分析,可以得出融合动态外部因素对模型性能的提升最为显著,静态因素对模型性能的提升有限,但相比于不使用任何外部因素,即仅使用路网图结构的情况,仍然有所改善。
| 数据集 | 模型设置 | 15 min | 30 min | 60 min | |||||
| RMSE | MAE | RMSE | MAE | RMSE | MAE | ||||
| SZ-TAXI | 消融模型1 | 4.07 | 2.75 | 4.11 | 2.78 | 4.17 | 2.84 | ||
| 消融模型2 | 4.03 | 2.70 | 4.05 | 2.74 | 4.10 | 2.80 | |||
| 消融模型3 | 4.01 | 2.66 | 4.01 | 2.71 | 4.04 | 2.81 | |||
| MSTGCN | 3.90 | 2.56 | 3.95 | 2.64 | 3.99 | 2.74 | |||
融合多源外部因素能够有效提高城市交通流预测精度。由于动态因素能够更好地表达交通流的时变特征,对模型性能的提升明显。本研究推测,该模型仅考虑了天气、是否属于高峰等因素,如果在模型中加入更多的动态因素,如社会事件、交通事故等因素,模型性能的提升将会更加显著。此外,静态因素对模型性能的提升也有一定的贡献,但相对较低。融合动态和静态因素对模型性能的贡献大于单一类型的因素,这说明动态和静态因素具有一定的互补性。
综上所述,本研究提出融合多源数据的多图时空图卷积网络模型MSGCNN能有效应对城市路网交通流预测任务,同时融合多源外部属性的模块能够有效提升模型的性能。
3 结论本研究首先对影响城市交通流的外部因素进行了明确且有结构的分类,并分析了这些因素对城市交通流的影响。在此基础上,介绍了一种用于城市路网交通流长时预测的融合多源数据的多图时空图卷积网络模型(MSGCNN)。该模型在建模交通流的时间相关性方面使用了门控循环单元,空间相关性方面使用了图卷积网络,并融合了静态和动态外部因素。试验证明该模型在不同指标和预测时长下相较于基准模型有更好的预测性能。本研究设计的消融试验,验证了融合静态因素的多图结构以及融合动态因素的全连接层对于模型预测性能的贡献。综上,本研究提出的融合多源数据的多图时空图卷积网络模型为城市交通流长时预测任务提供了一种有效的解决方案和思路,对于未来城市交通流预测任务具有实际意义和研究价值。
| [1] |
EDES Y J S, MICHALOPOULOS P G, PLUM R A. Improved Estimation of Traffic Flow for Real-time Control[J].
Transportation Research Record, 1981, 7(9): 28-39.
|
| [2] |
王九胜, 戴许海, 缪中岩, 等. 基于多元时空关系的公路交通流量时序预测模型[J]. 公路交通科技, 2023, 40(10): 175-182. WANG Jiu-sheng, DAI Xu-hai, MIAO Zhong-yan, et al. A Model for Time Series Prediction on Highway Traffic Flow Based on Multivariate Spatio-temporal Relationship[J]. Journal of Highway and Transportation Research and Development, 2023, 40(10): 175-182. DOI:10.3969/j.issn.1002-0268.2023.10.020 |
| [3] |
祁朵, 毛政元. 基于自适应时序剖分与KNN的短时交通流量预测[J]. 地球信息科学学报, 2022, 24(2): 339-351. QI Duo, MAO Zheng-yuan. Short-term Traffic Flow Prediction Based on Adaptive Time Series Subdivision and KNN[J]. Journal of Geo-Information Science, 2022, 24(2): 339-351. |
| [4] |
于德新, 邱实, 周户星, 等. 基于GRU-RNN模型的交叉口短时交通流预测研究[J]. 公路工程, 2020, 45(4): 109-114. YU De-xin, QIU Shi, ZHOU Hu-xing, et al. Research on Short-term Traffic Flow Prediction of Intersections Based on the GRU-RNN Model[J]. Highway Engineering, 2020, 45(4): 109-114. |
| [5] |
王磊, 王永华, 何一汕, 等. 基于GRU和LSTM组合模型的车联网信道分配方法[J/OL]. 电讯技术(2022-11-10)[2023-07-01]. http://kns.cnki.net/kcms/detail/51.1267.tn.20221109.1438.006.html. WANG Lei, WANG Yong-hua, HE Yi-shan, et al. Channel Allocation Method for Vehicle-to-everything Based on GRU and LSTM Combined Model[J/OL]. Telecommunication Engineering (2022-11-10)[2023-07-01]. http://kns.cnki.net/kcms/detail/51.1267.tn.20221109.1438.006.html. |
| [6] |
赵建东, 申瑾, 刘麟玮. 多源数据驱动CNN-GRU模型的公交客流量分类预测[J]. 交通运输工程学报, 2021, 21(5): 265-273. ZHAO Jian-dong, SHEN Jin, LIU Lin-wei. Bus Passenger Flow Classification Prediction Driven by CNN-GRU Model and Multi-source Data[J]. Journal of Traffic and Transportation Engineering, 2021, 21(5): 265-273. |
| [7] |
PAN Y Y, GUO J F, CHEN Y Y, et al. Incorporating Traffic Flow Model into A Deep Learning Method for Traffic State Estimation: A Hybrid Stepwise Modeling Framework[J].
Journal of Advanced Transportation, 2022, 253362833.
|
| [8] |
CUI Z, HUANG B, DOU H, et al. GSA-ELM: A Hybrid Learning Model for Short-term Traffic Flow Forecasting[J].
IET Intelligent Transport Systems, 2022, 16(1): 41-52.
DOI:10.1049/itr2.12127 |
| [9] |
HOU Q, LENG J, MA G, et al. An Adaptive Hybrid Model for Short-term Urban Traffic Flow Prediction[J].
Physica A: Statistical Mechanics and its Applications, 2019, 527: 121065.
DOI:10.1016/j.physa.2019.121065 |
| [10] |
CHENG G F, LI X, YAN Y H. Using Highway Connections to Enable Deep Small-footprint LSTM-RNNs for Speech Recognition[J].
Chinese Journal of Electronics, 2019, 28(1): 107-112.
DOI:10.1049/cje.2018.11.008 |
| [11] |
殷齐, 丁飞, 朱跃, 等. 基于CNN与多尺度特征融合的城市交通流预测模型[J]. 计算机技术与发展, 2022, 32(10): 175-181. YIN Qi, DING Fei, ZHU Yue, et al. An Urban Traffic Flow Prediction Model Based on CNN and Multi-scale Feature Fusion[J]. Computer Technology and Development, 2022, 32(10): 175-181. DOI:10.3969/j.issn.1673-629X.2022.10.029 |
| [12] |
施俊庆, 陈林武, 李素兰, 等. 基于CNN的城市道路交通事件检测算法[J]. 公路交通科技, 2022, 39(3): 176-182. SHI Jun-qing, CHEN Lin-wu, LI Su-lan, et al. Urban Road Traffic Event Detection Algorithm Based on CNN[J]. Journal of Highway and Transportation Research and Development, 2022, 39(3): 176-182. DOI:10.3969/j.issn.1002-0268.2022.03.022 |
| [13] |
张雄涛, 郑景玉, 申情, 等. 基于混合图卷积的多通道时空交通流预测模型[J]. 电信科学, 2023, 39(9): 97-110. ZHANG Xiong-tao, ZHENG Jing-yu, SHEN Qing, et al. Multi-channel Spatial-temporal Traffic Flow Prediction Based on Hybrid Static-dynamic Graph Convolution[J]. Telecommunications Science, 2023, 39(9): 97-110. |
| [14] |
贺文武, 裴博彧, 李雅婷, 等. 基于双向自适应门控图卷积网络的交通流预测[J]. 交通运输系统工程与信息, 2023, 23(1): 187-197. HE Wen-wu, PEI Bo-yu, LI Ya-ting, et al. Traffic Flow Forecasting Based on Bi-direction Adaptive Gating Graph Convolutional Networks[J]. Journal of Transportation Systems Engineering and Information Technology, 2023, 23(1): 187-197. |
| [15] |
ZHAO L, SONG Y J, ZHANG C, et al. T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction[J].
IEEE Transactions on Intelligent Transportation Systems, 2019, 21(9): 3848-3858.
|
| [16] |
ZHU J, WANG Q, TAO C, et al. AST-GCN: Attribute-augmented Spatiotemporal Graph Convolutional Network for Traffic Forecasting[J].
IEEE Access, 2021, 9: 35973-35983.
DOI:10.1109/ACCESS.2021.3062114 |
| [17] |
LIAO B B, ZHANG, J Q, WU C, et al. Deep Sequence Learning with Auxiliary Information for Traffic Prediction[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. London: Association for Computing Machinery, 2018, 537-546.
|
| [18] |
ZHANG D, KABUKA M R. Combining Weather Condition Data to Predict Traffic Flow: A GRU-based Deep Learning Approach[J].
IET Intelligent Transport Systems, 2018, 12(7): 578-585.
DOI:10.1049/iet-its.2017.0313 |
| [19] |
YU B, YIN H T, ZHU Z X. Spatio-temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting[C]//Proceedings of the Twenty Seventh International Joint Conference on Artificial Intelligence. Stockholm: IJCAI, 2018: 3634-3640.
|
| [20] |
VLAHOGIANNI E I, KARLAFTIS M G, GOLIAS J C. Short-term Traffic Forecasting: Where We Are and Where We're Going[J].
Transportation Research Part C: Emerging Technologies, 2014, 43: 3-19.
DOI:10.1016/j.trc.2014.01.005 |
| [21] |
LI Y G, YU R, SHAHABI C, et al. Diffusion Convolutional Recurrent Neural Network: Data-driven Traffic Forecasting[C]//ICLR 2018. Vancouver: arXiv, 2018.
|
| [22] |
YUAN H, LI G. A Survey of Traffic Prediction: From Spatio-temporal Data to Intelligent Transportation[J].
Data Science and Engineering, 2021, 6(1): 63-85.
DOI:10.1007/s41019-020-00151-z |
 2024, Vol. 41
2024, Vol. 41
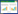


 ,
,